一种低输入电流总谐波畸变率的三相Buck整流器不对称调制策略

曹海彬 许建平 谢 飞 周琛力 陈 欣

一种低输入电流总谐波畸变率的三相Buck整流器不对称调制策略

曹海彬 许建平 谢 飞 周琛力 陈 欣

（西南交通大学电气工程学院磁浮技术与磁浮列车教育部重点实验室 成都 610031）

传统空间矢量脉宽调制（SVPWM）三相Buck整流器没有考虑直流链电流纹波对输入电流的影响，且在扇区切换点处输入电流存在严重畸变，导致输入电流总谐波畸变率（THD）升高。该文分析直流链电流纹波对三相Buck整流器输入电流的影响，分析输入电流扇区切换点畸变产生的原因，提出一种新型不对称SVPWM策略，显著降低了三相Buck整流器的输入电流THD。最后，通过仿真和1 kW的实验样机验证了理论分析的正确性以及所提调制策略的有效性。

三相Buck整流器 直流链电流纹波 输入电流畸变 不对称调制策略

0 引言

三相整流器主要分为三相Boost整流器和三相Buck整流器[1-4]。相较于三相Boost整流器，三相Buck整流器具有固有的启动浪涌电流抑制能力和短路保护能力，可靠性较高，易于并联[5-6]，可实现单级降压整流，因此，三相Buck整流器广泛应用在多电飞机[7-8]、电动汽车[9-10]以及地面数据中 心[11-12]等场合。

输入电流总谐波畸变率（Total Harmonic Dis- tortion, THD）是三相Buck整流器的重要性能指标，它主要由整流器电路拓扑以及调制和控制技术决定。在控制技术及拓扑结构方面，对输入电流THD的研究主要集中在输入滤波器振荡、三相输入不平衡以及共模电流干扰等工况。文献[13]通过引入电容电压反馈有源阻尼控制环路，明显降低了输入滤波器振荡带来的网侧电流畸变。在文献[13]的基础上，文献[14]通过在内环引入直流侧电感电流反馈以及阻尼因子，进一步改善了网侧LC谐振带来的输入电流畸变。文献[15]提出了一种新型三相不平衡控制策略，利用三相Buck整流器的传递矩阵模型有效降低了不平衡条件下三相输入电流THD。文献[16]提出一种新颖的三相Buck整流器拓扑，通过分析高功率密度整流器的共模电流对输入电流的影响，提出一种针对三相Buck整流器的共模滤波器，明显削弱了共模电流对输入电流THD的影响。

三相Buck整流器输入电流THD除受控制技术及拓扑结构的影响，还与调制策略有关，因此，研究三相Buck整流器的调制策略以优化输入电流THD具有重要意义。目前主要的调制策略有特定谐波消除法、梯形脉宽调制策略、正弦脉宽调制策略以及空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）策略，SVPWM策略的应用最为广泛[17]。文献[18]提出一种最优开关损耗调制策略，在保证高效率的同时，消除了三相桥臂全部导通时开关状态所引起的输入电流畸变。文献[19]提出了一种适用于断续导通模式（Discontinuous Conduction Mode, DCM）和连续导通模式（Con- tinuous Conduction Mode, CCM）的有效矢量占空比计算方法，有效解决了DCM三相Buck整流器的输入电流畸变，并且不存在DCM和CCM占空比计算方法的切换。文献[20-21]通过对有效矢量进行切分，降低直流链电流纹波，达到优化输入电流THD的效果。

然而，上述SVPWM均将直流链电流假设为恒定值，然后进行有效矢量作用时间的计算，忽略了直流链电流纹波对输入电流的影响。在实际应用中，为了提高动态性能和功率密度，三相Buck整流器的输出电感取值较小，这导致三相Buck整流器的直流链电流纹波较大，此时直流链电流纹波对输入电流质量的影响愈发明显。

此外，传统SVPWM三相Buck整流器输入电流存在严重的扇区切换点畸变，为了解决这一问题，可以增加扇区切换点处的开关频率和对扇区切换点处的驱动信号脉宽进行单独处理[22]，然而，这两种方法都不能完全消除扇区切换点畸变。

本文首先通过各矢量作用时三相桥臂的输入电流，分析了直流链电流纹波对输入电流的影响；然后通过扇区切换点处的驱动信号过渡过程分析了输入电流扇区切换点畸变产生的原因；最后提出了一种新型的不对称SVPWM策略，在考虑直流链电流纹波对输入电流影响的基础上，消除了扇区切换点畸变，显著降低了输入电流THD。本文通过仿真和实验验证了所提出不对称调制策略的正确性。

1 传统SVPWM

图1给出了三相六开关Buck整流器电路及其控制结构，三相六开关Buck整流器主要由输入滤波器L和C（=a, b, c）、六个桥臂、一个续流二极管VDF以及输出滤波器组成。图1中，每个桥臂都由一个MOSFET Q和一个二极管VD（=1, …, 6）串联构成。v和i分别为三相输入电压和输入电流，s_x为三相桥臂的输入电流，dc为直流链电流，o为输出电压。控制结构采用间接电流控制，调制波由输入电压经计算得到，驱动信号占空比与输入电压成正比。

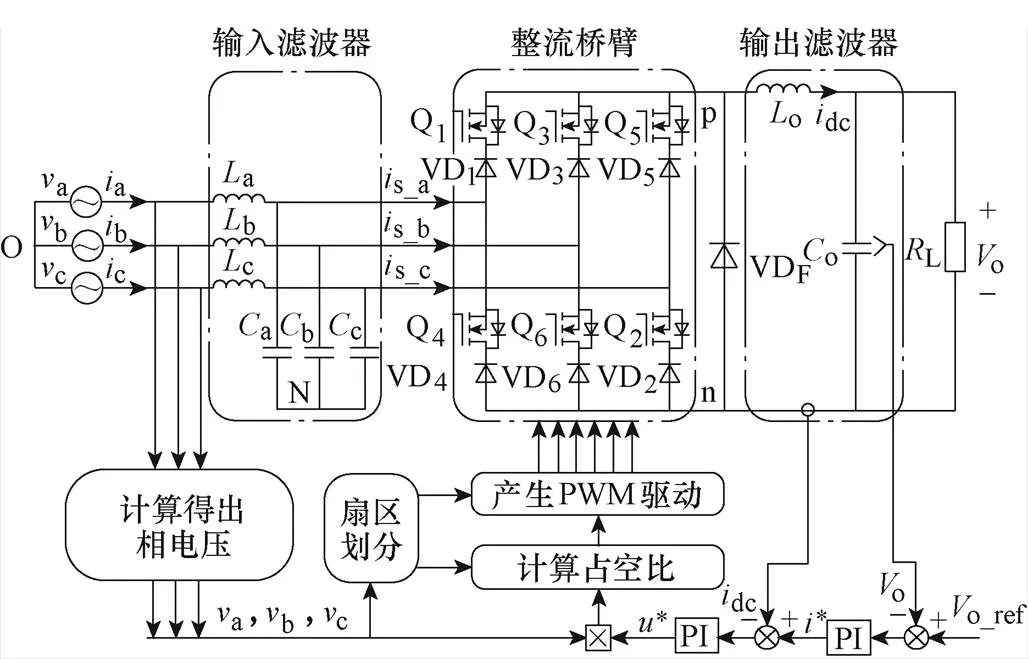
图1 三相Buck整流器主拓扑

图2给出了SVPWM的十二扇区划分方法，它由传统六扇区调制的每个扇区均等分为两个部分所得到，可以在不改变开关频率的情况下，明显提升三相Buck整流器的效率[23]。根据六个桥臂的开关状态形成十种三相Buck整流器工作状态，对应SVPWM的十种空间矢量1～10，其中1～6为有效矢量，7～10为零矢量，10对应的工作状态为桥臂中所有开关器件关断。为目标矢量ref与a轴的夹角，下面称为矢量角。每个有效矢量作用时，都对应一个特定的续流二极管两端电压pn；每个零矢量作用时，续流二极管两端电压为零。具体的空间矢量与pn的对应关系见表1。

图2 十二扇区空间矢量

表1 空间矢量与对应的开关状态

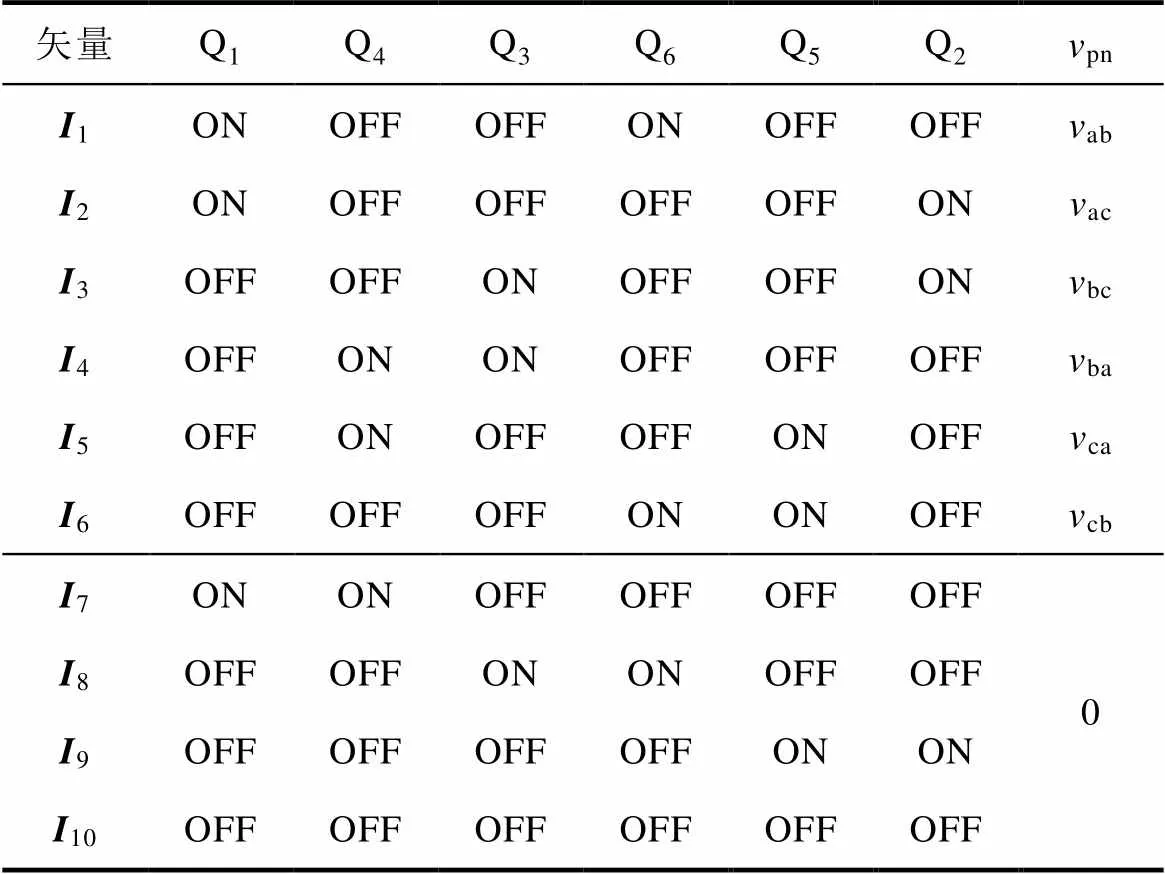
Tab.1 Space vectors and corresponding switching states

与空间划分的扇区相对应，传统SVPWM也将一个输入周期分成12个扇区，以A相电压达到正的峰值为扇区1的起始点，每隔30°为一个扇区。输入相电压与扇区分布关系如图3所示，图3中，m为输入相电压的峰值。

图4给出了四种应用于三相Buck整流器的传统SVPWM，按驱动信号是否关于开关周期中心对称，传统SVPWM分为不对称SVPWM和对称SVPWM[23]，图4a和图4b是不对称SVPWM，图4c和图4d是对称SVPWM。

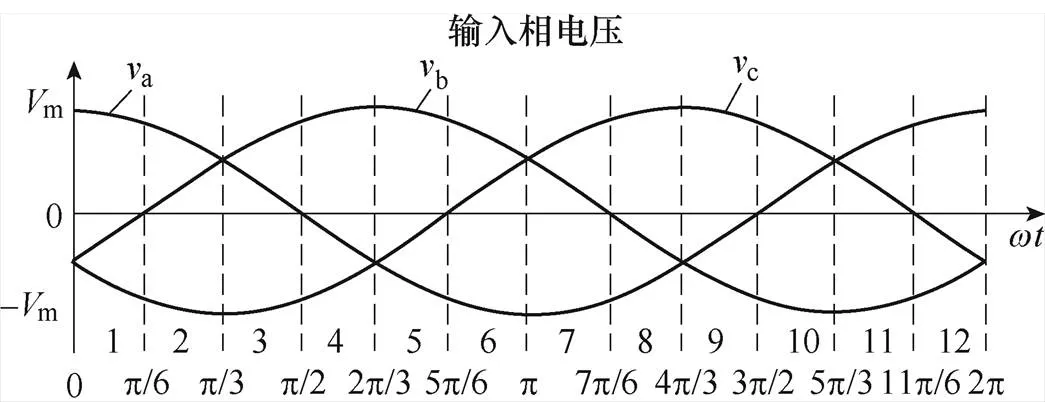
图3 输入相电压与扇区分布

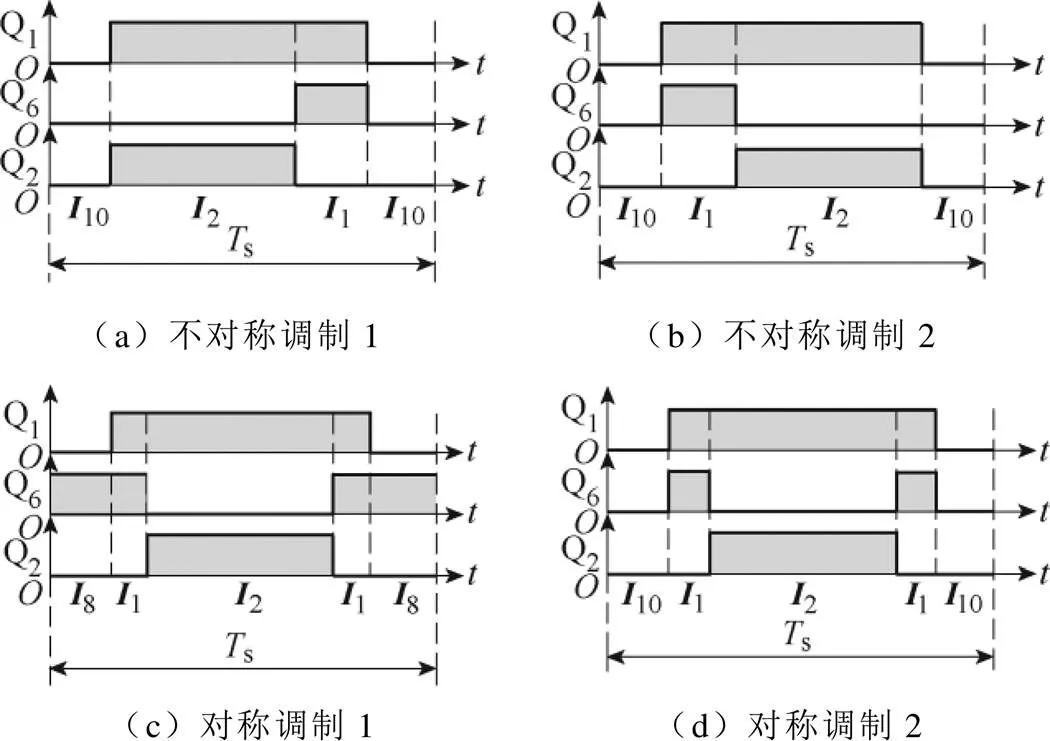
图4 三相Buck整流器传统SVPWM策略

2 直流链电流纹波对输入电流质量的影响

2.1 三相Buck整流器工作状态

图5给出了扇区1的三种空间矢量1、2及8（或10）对应的三相Buck整流器工作状态。

由图5a可知，整流器工作在矢量1时，Q1和Q6导通，直流链电流从A相输入滤波器流出，经开关器件Q1、直流链o、负载L以及开关器件Q6流回B相输入滤波器。A相桥臂输入电流s_a为直流链电流，B相桥臂输入电流s_b为负的直流链电流，线电压ab为续流二极管VDF两端电压。

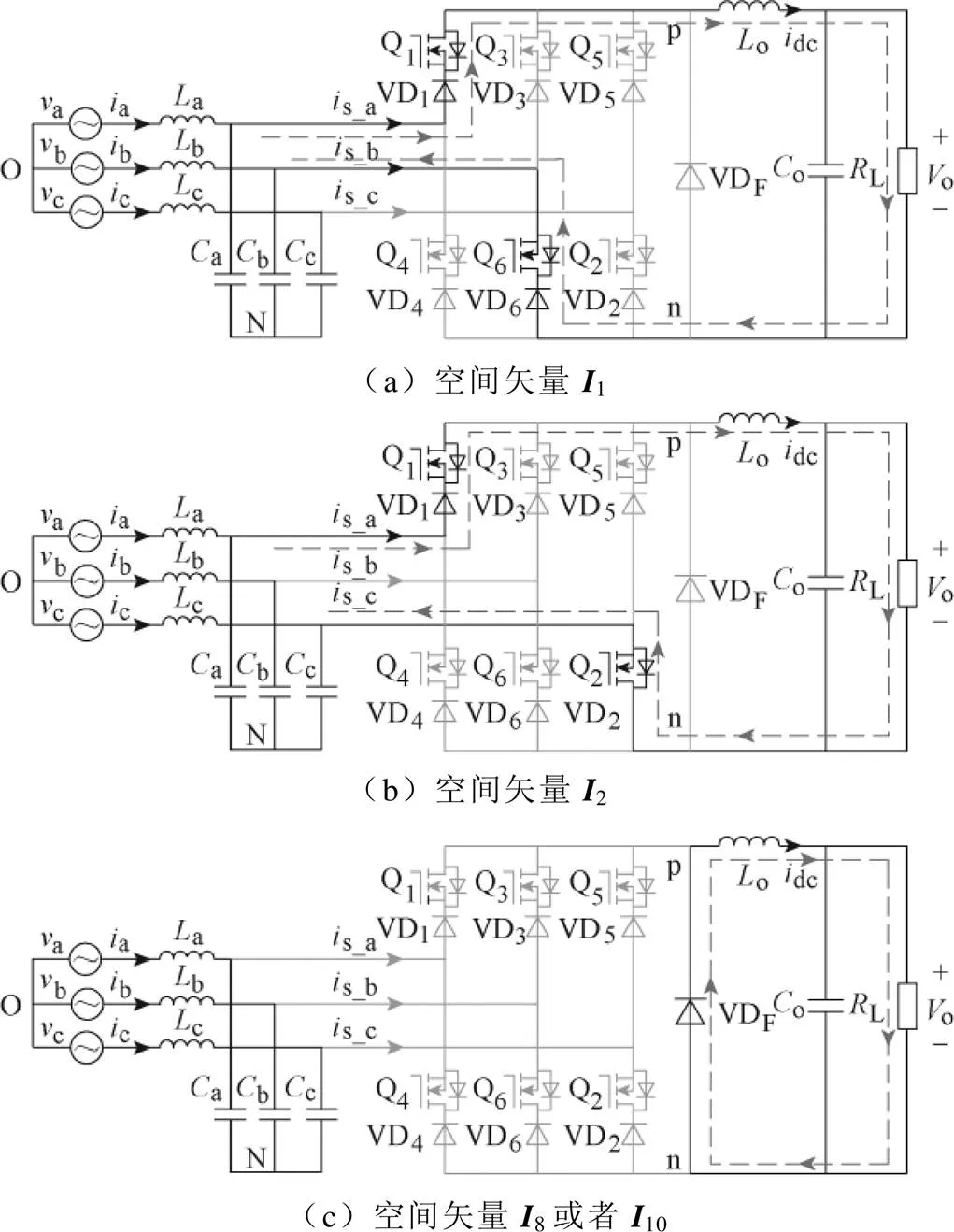
图5 扇区1内空间矢量对应的工作状态

由图5b可知，整流器工作在矢量2时，Q1和Q2导通，直流链电流从A相输入滤波器流出，经开关器件Q1、直流链o、负载L以及开关器件Q2流回C相输入滤波器。A相桥臂输入电流s_a等于直流链电流，C相桥臂输入电流s_c等于负的直流链电流，续流二极管VDF两端电压为输入线电压ac。

由图5c可知，在零矢量作用期间，直流链电流经续流二极管续流，不流向输入侧，此时三相桥臂的输入电流均为零，续流二极管VDF两端电压为0。

2.2 直流链电流纹波的计算

根据图1所示三相Buck整流器拓扑可知，直流链电流变化量DI可以表示为

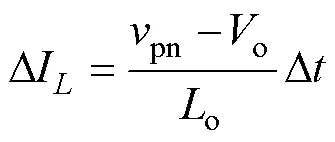
式中，o为直流侧输出电压；o为输出滤波电感；D为输出滤波电感的充电或者放电时间。

在扇区1的一个开关周期内，有效矢量1、2以及零矢量的作用时长分别为

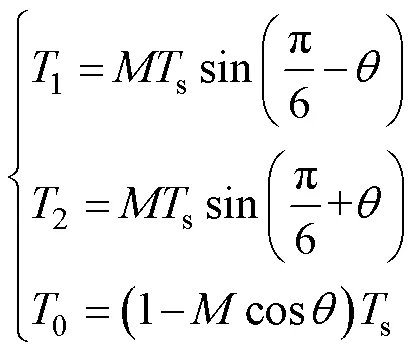
式中，s为开关周期；取值范围为0～p/6；为调制度，其表达式为

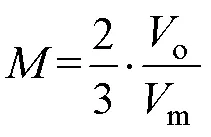
三相线电压的数学表达式为

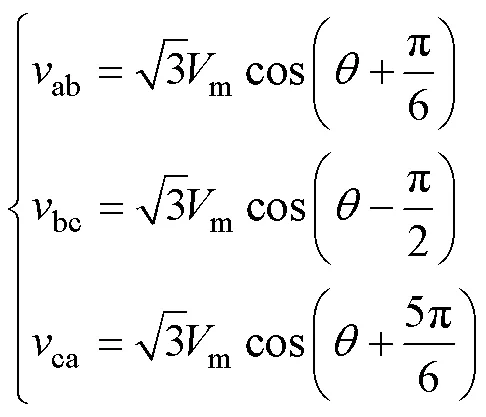
由图5可知，ab为矢量1对应的续流二极管两端电压pn1，ac为矢量2对应的续流二极管两端电压pn2，矢量8对应的续流二极管两端电压pn0为0。因此，扇区1中三种矢量对应的续流二极管两端电压pn可表示为

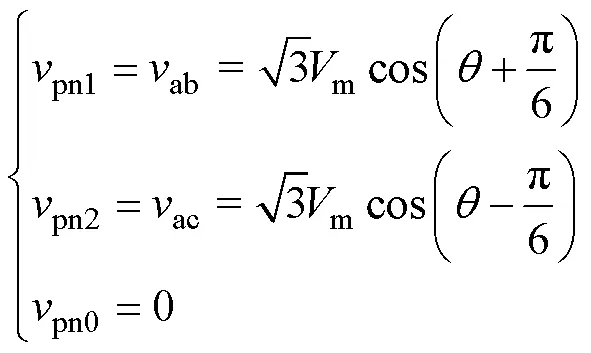
基于以上分析，扇区1中三种矢量对应的直流链电流的纹波部分DI1、DI2和DI0可分别表示为

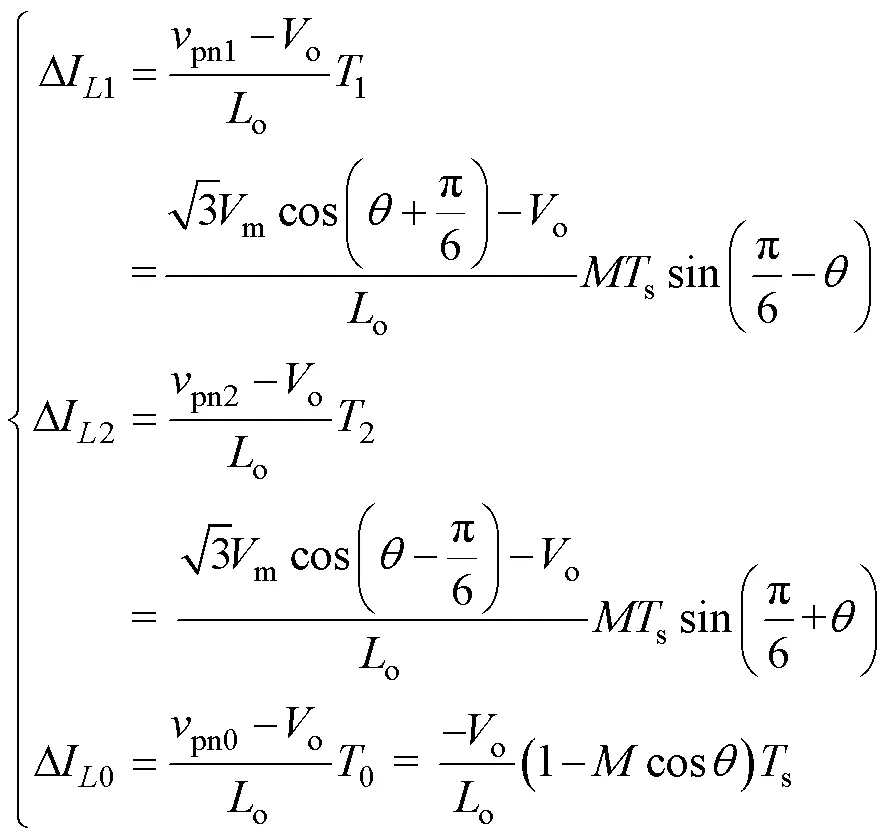
由式（6）可知，开关频率一定时，直流链电流纹波与调制度、矢量角和输出滤波电感o有关。

2.3 直流链电流纹波对输入电流质量的影响

为了保证直流链电流的唯一性，假设在扇区1仅空间矢量2作用期间续流二极管两端电压pn大于输出电压。结合第2.1节的三相Buck整流器工作状态和式（6），可以得到一个开关周期内不对称调制1和对称调制1的直流链电流波形以及三相桥臂的输入电流，如图6和图7所示。

图6给出了扇区1中不对称调制1对应三相桥臂的输入电流波形。图6中，dc_a为直流链电流平均值，s_a、s_b和s_c中深色阴影部分为其平均等效电流。由图6可知，在一个开关周期内，s_a和s_b的平均等效电流幅值大于直流链电流平均值，其中s_b的平均等效电流最大，s_c的平均等效电流幅值小于直流链电流平均值；三相桥臂输入平均等效电流作用时长与桥臂驱动信号脉宽相等。因此，根据面积等效原理，三相桥臂的输入平均等效电流与对应相占空比的比值不相等，即经输入滤波器滤波后得到的三相输入电流与对应相占空比的比值不相等，即与对应相输入电压的比值不相等，这势必会造成输入电流的畸变以及谐波含量的增加。在其他扇区中这一结论依然成立。

图6 扇区1内不对称调制1的三相桥臂输入电流

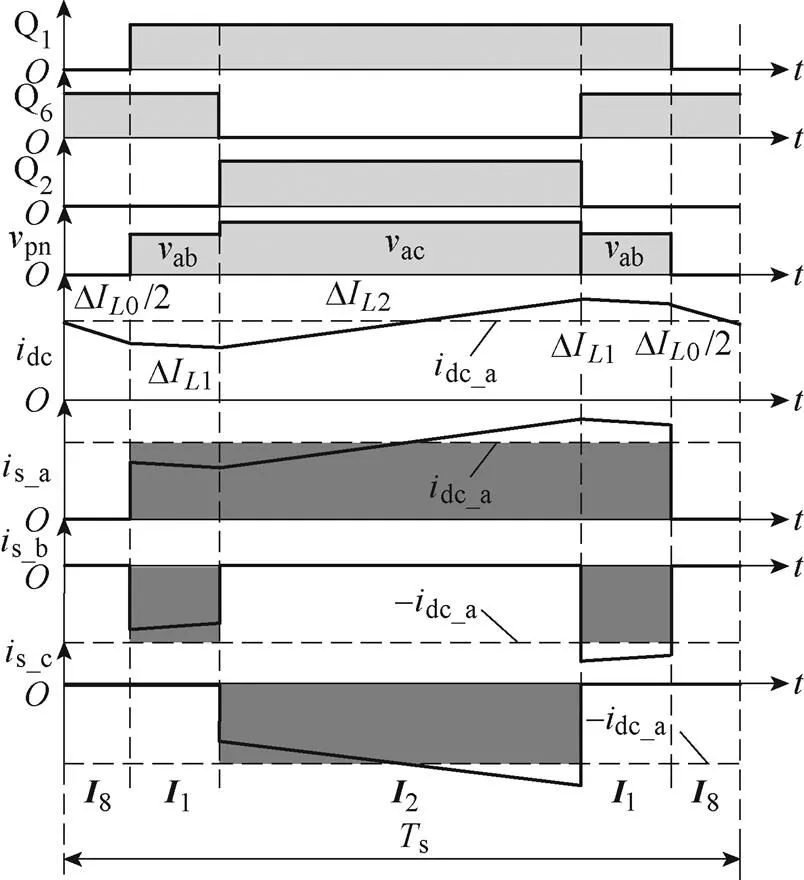
图7 扇区1内对称调制1的三相桥臂输入电流

同理可得，采用对称调制1时，扇区1中三相桥臂的输入电流波形，如图7所示。由图7可知，一个开关周期内，三相桥臂的输入平均等效电流幅值等于直流链电流平均值，且桥臂输入平均等效电流作用时长与对应相的驱动信号脉宽相等。因此，根据面积等效原理，经输入滤波器滤波后得到的三相输入电流与对应相占空比的比值相等，即与对应相输入电压的比值相等，输入电流中的谐波含量较少。其他扇区中，这一结论依然成立。

不对称调制2和对称调制2可以按照相同的方法进行分析，并且拥有相似的分析结果：传统不对称调制三相Buck整流器的输入电流含有较严重的谐波成分；而传统对称调制三相Buck整流器的输入电流的谐波成分较少。

3 输入电流扇区切换点畸变的原因分析

以扇区12和扇区1的切换点为例，进行输入电流扇区切换点畸变的原因分析。图8给出了扇区12和扇区1不对称调制1的PWM序列。

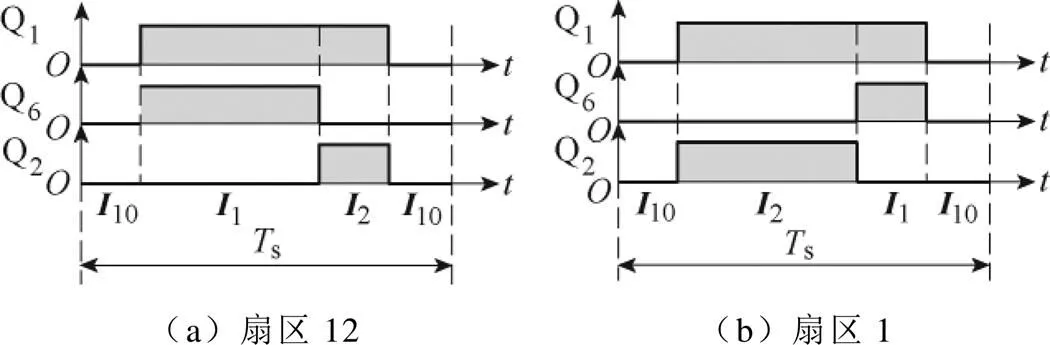
图8 不对称调制1的PWM序列

文献[22]给出了调制度的另外一种表达式为

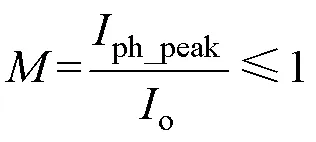
式中，ph_peak为输入相电流的峰值；o为输出电流。在实际应用中，调制度应取一定裕度，即直流链电流的平均值始终大于输入电流。

结合图5和式（7），在扇区12和扇区1，矢量1、2和10作用时输入滤波器中电流路径如图9所示。由图9a可知，当矢量1作用时，输入滤波电容a放电，a两端电压a下降，输入滤波电感a两端电压a上升；输入滤波电容b充电，b两端电压b上升，输入滤波电感b两端电压b下降；输入滤波电容c放电，c两端电压c下降，输入滤波电感c两端电压c上升。

同理可得，矢量2作用时，输入滤波电感a两端电压a上升，输入滤波电感b两端电压b上升，输入滤波电感c两端电压c下降。矢量10作用时，输入滤波电感a两端电压a下降，输入滤波电感b两端电压b上升，输入滤波电感c两端电压c上升。

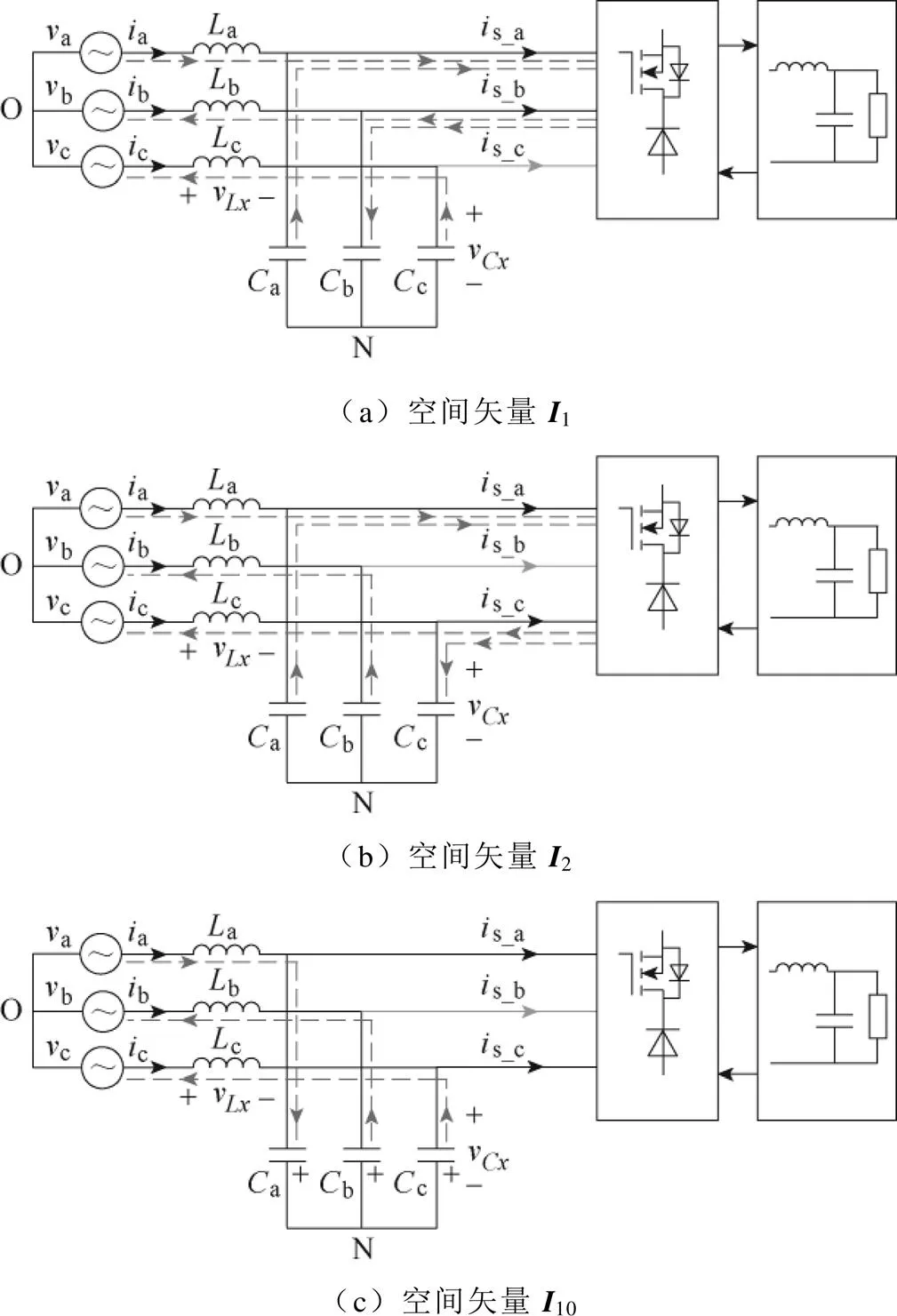
图9 扇区1内空间矢量对应的输入滤波器电流路径

图10给出了采用不对称调制1的三相Buck整流器在扇区12和扇区1切换点处的输入滤波电感电压和电流。在扇区12和扇区1中，驱动信号即PWM序列不同，从扇区12切换到扇区1时，在切换点附近连续出现两个矢量1。根据上面分析可知，矢量1作用时长的增加将导致B相输入滤波电感电压连续下降，在较长时间内为负电压，输入滤波电感电流b迅速减小，同理C相输入滤波电感电流c迅速增大，形成畸变。在扇区切换点处PWM序列的改变不影响A相输入滤波电感电压va，A相输入滤波电感电流a中没有畸变。无论扇区更新点位于开关周期中心左侧还是右侧均会造成B相电感电流迅速下降和C相电感电流迅速上升，形成畸变。

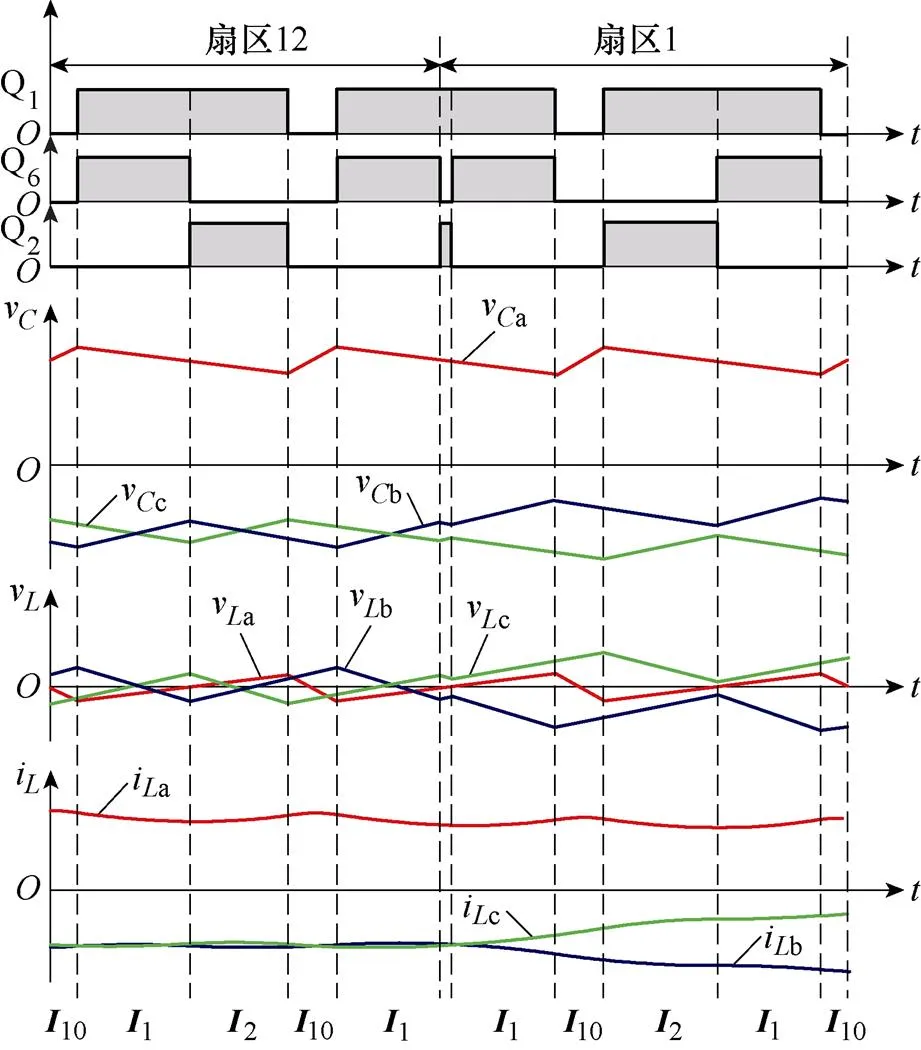
图10 传统不对称调制1在扇区切换点处的输入滤波电感电压和电流

假设扇区更新点在开关周期中心的左侧，对称调制1在扇区12和扇区1切换点处的输入滤波电感电压和电流波形如图11所示。由图11可知，在扇区切换点附近出现两个相距较近的矢量2，导致B相输入滤波电感电压在较长时间内大于零，B相输入滤波电感电流b迅速增大；C相输入滤波电感电压在较长时间内小于零，C相输入滤波电感电流c迅速减小，形成畸变。与传统不对称调制1类似，A相输入滤波电感电流a中没有畸变产生。若扇区更新点位于开关周期中心右侧，则在扇区切换点处出现两个相距较近的矢量1，造成B相电感电流b迅速下降和C相电感电流c迅速上升，形成畸变。

图11 传统对称调制1在扇区切换点处的输入滤波电感电压和电流

与不对称调制1和对称调制1相似，不对称调制2和对称调制2在扇区切换点也存在输入电流畸变。因此，无论是传统对称调制还是传统不对称调制，三相Buck整流器的输入电流中均存在扇区切换点畸变，导致输入电流THD恶化。

4 一种新型不对称调制策略

4.1 新型不对称调制策略

本文提出一种新型的不对称调制策略，该调制策略不仅考虑了直流链电流纹波对输入电流质量的影响，还消除了传统调制存在的扇区切换点畸变问题，改善了三相Buck整流器的输入电流THD。

图12给出了本文提出的调制策略在A相电压大于零的六个扇区（扇区10、扇区11、扇区12、扇区1、扇区2和扇区3）的PWM序列。本文提出的不对称调制策略将零矢量均等的分为两个部分，并将其中一部分插入在两个有效矢量中间。由图12可知，在扇区10和扇区11，矢量的作用顺序为：6—8—1—10—6；在扇区12和扇区1，矢量的作用顺序为：2—7—1—10—2；在扇区2和扇区3，矢量的作用顺序为：2—9—3—10—2。

图12 提出的不对称调制策略

A相电压小于零的六个扇区（扇区4、扇区5、扇区6、扇区7、扇区8和扇区9）的矢量作用顺序为：扇区4和扇区5（4—8—3—10—4）、扇区6和扇区7（4—7—5—10—4）、扇区8和扇区9（6—9—5—10—6）。

4.2 低谐波含量输入电流

由2.2节分析可知，每个矢量都对应一个电感电流的上升量D。扇区1中有效矢量1对应的直流链电流上升量为D1、零矢量对应的直流链电流上升量为D0、有效矢量2对应的直流链电流上升量为D2。三相Buck整流器稳定工作时，一个开关周期内电感电流的起始值等于其结束值，则三种矢量对应的D之间满足

图13给出了本文提出的不对称调制在扇区1的直流链电流波形，由图13可知，从矢量2的中点到矢量1的中点，电感电流的上升量DT为

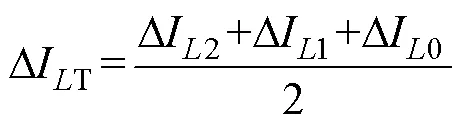
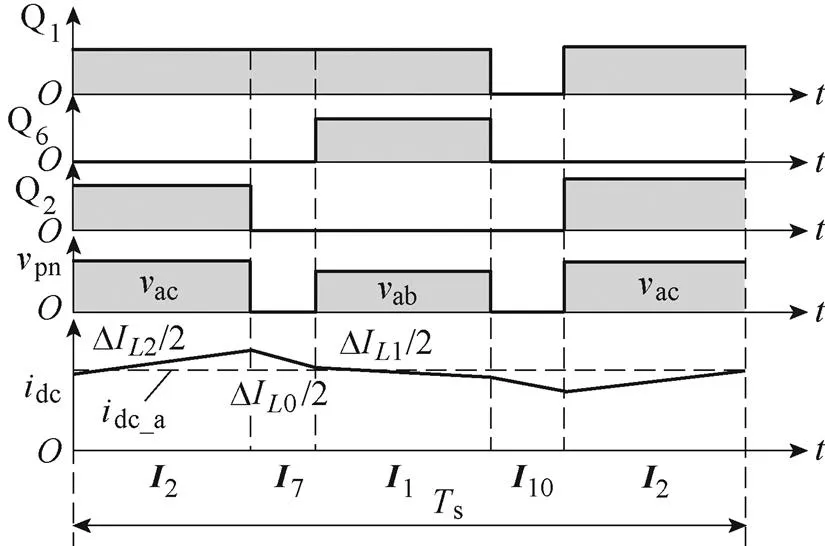
图13 扇区1内提出的不对称调制的直流链电流

结合式（8）和式（9）可知，电感电流的上升量DT=0，即矢量2和矢量1对应的电感电流平均值相等，且等于直流链电流平均值。

图14给出了本文提出的不对称调制在扇区1的三相桥臂输入电流波形。由图14可知，A相桥臂的输入电流为矢量1和矢量2对应的电感电流之和，B相桥臂的输入电流为矢量1对应的电感电流，C相桥臂的输入电流为矢量2对应的电感电流。由上面的分析可知，三相桥臂输入平均等效电流幅值均等于直流链电流平均值，并且输入平均等效电流的时长等于对应的三相桥臂驱动信号的脉宽。因此，根据面积等效原理，三相桥臂输入电流与对应相占空比的比值相等，即三相输入电流与对应相输入电压的比值相等。在其他扇区中这一结论依然成立，因此，相较于传统不对称调制1，输入电流中具有较少的谐波含量。

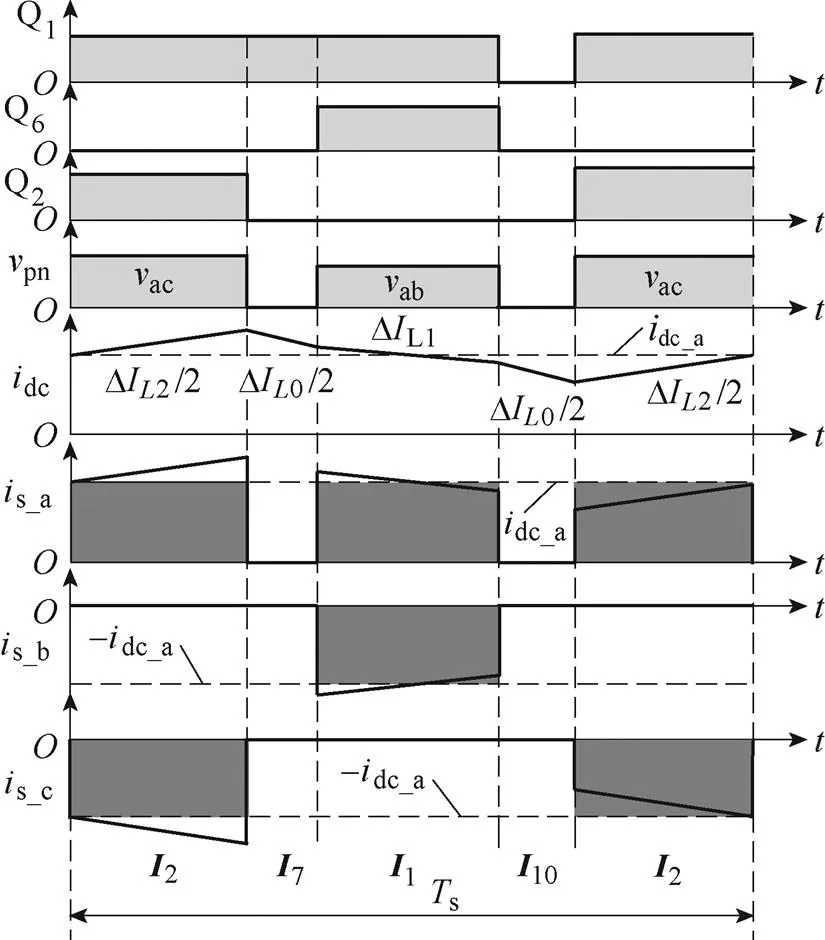
图14 扇区1内提出的不对称调制的三相桥臂输入电流

4.3 输入电流扇区切换点畸变的消除

在数字处理器中，扇区切换时，驱动信号从当前PWM序列强制转换成下一个扇区的PWM序列。此时，如果两个扇区的PWM序列不同，将导致偶扇区向奇扇区切换时，某个矢量在较短时间内连续作用，且每个矢量对应的输入滤波电感电流变化情况是固定的。因此，某个矢量的连续作用意味着输入滤波电感电流连续上升或者下降，形成输入电流畸变。

在相邻偶扇区和奇扇区，提出的不对称调制策略的PWM序列一致，因此无论在开关周期内任何位置切换到下一个扇区，三相桥臂的驱动信号均能平滑过渡。

图15给出了提出的不对称调制在扇区12和扇区1切换点处的输入滤波电感电压和电流波形，由图15可知，扇区的切换并不影响本文提出的不对称PWM驱动波形，即三相输入滤波电感电压和电流波形平滑过渡。因此，三相输入电流中没有扇区切换点畸变。

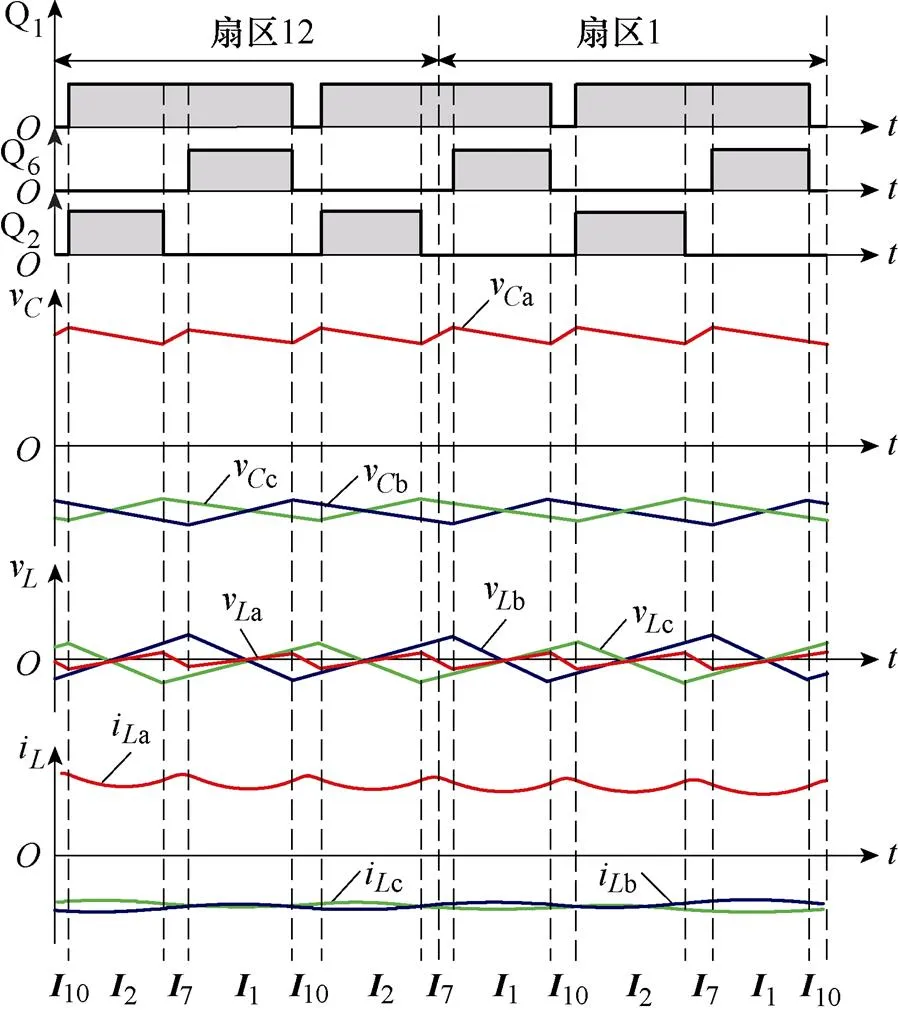
图15 提出的不对称调制在扇区切换点处的输入滤波电感电压和电流

综上所述，本文提出的调制策略既保留了传统对称调制输入电流中谐波含量较低的优点，还消除了传统调制存在的输入电流扇区切换点畸变，进一步优化了三相输入电流THD。

5 仿真与实验验证

5.1 仿真证明

为了验证上面提到的理论分析，通过仿真软件PSIM对传统调制和本文提出的不对称调制进行仿真验证。主要电路参数见表2。

表2 主要电路参数

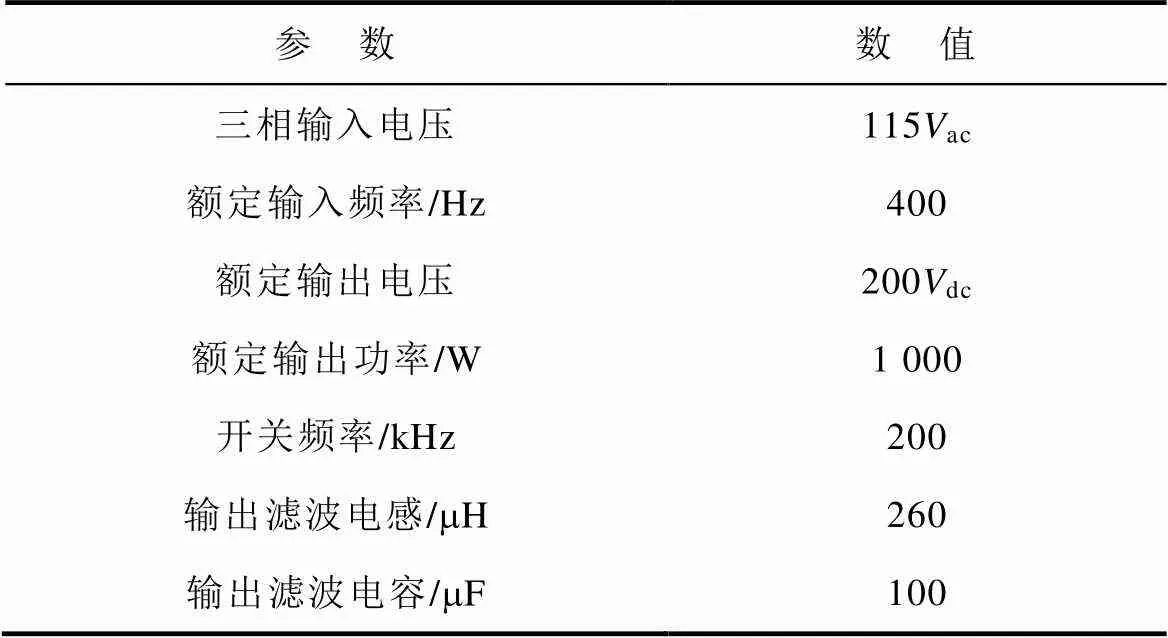
Tab.2 Main parameters of the circuit

由式（6）可知，直流链电流纹波只与输入电压、输出电感、输出电压以及各矢量的作用时间有关，而与负载大小无关。因此，随着输出电流的增大，直流链电流纹波与直流链电流平均值的比值下降，直流链电流纹波对输入电流质量的影响减弱。因此，仿真以50%负载进行。

图16给出了50%负载条件下，采用传统不对称调制1的三相Buck整流器输入电流以及扇区12和扇区1切换点处的驱动信号过渡过程。由图16a可知，输入电流THD=4.9%，三相输入电流波形畸变严重，且在偶数扇区切换到奇数扇区的六处扇区切换点出现畸变。由图16b可知，在扇区12切换扇区1处，两个扇区的2连续作用，造成B相输入电流迅速下降，C相输入电流迅速上升，形成畸变。

图17给出了采用传统对称调制1的三相输入电流以及扇区12和扇区1切换点处的驱动信号过渡过程。由图17a可知，相较于上面的传统不对称调制1，采用传统对称调制1的三相Buck整流器的输入电流THD更优，仅为2.3%，但是依然存在六处扇区切换点畸变。由图17b可知，在扇区12切换扇区1处，出现两个相距较近的矢量2，造成B相输入电流迅速上升，C相输入电流迅速下降，形成畸变。

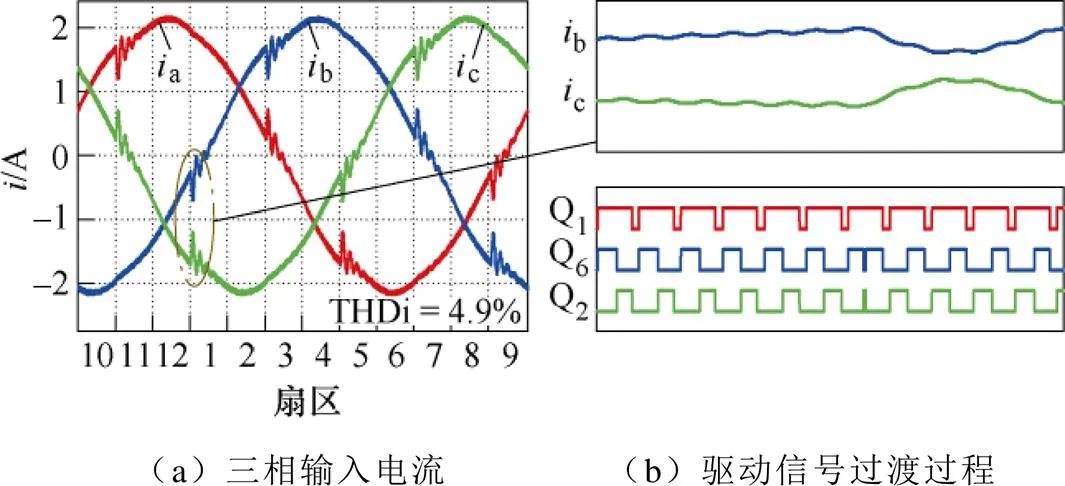
图16 传统不对称调制1的仿真结果

图17 传统对称调制1的仿真结果

图18给出了采用本文提出的不对称调制的三相Buck整流器的输入电流以及扇区12和扇区1切换点处的驱动信号过渡过程。由图18a和图18b可知，输入电流THD仅为1.7%，三相输入电流正弦度高且扇区切换点处驱动波形平滑过渡，B相和C相输入电流无畸变。

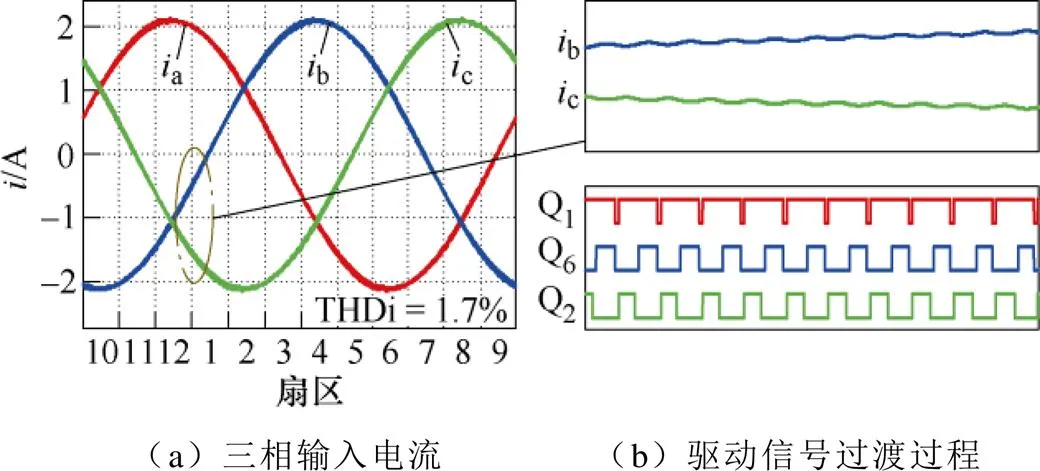
图18 提出的不对称调制的仿真结果

综上所述，本文提出的不对称调制不仅保留了传统对称调制输入电流正弦度高的优点，还消除了扇区切换点畸变，进一步优化了输入电流THD。

5.2 实验验证

为进一步验证本文提出的调制策略的正确性和实用性，设计制作了一台1 kW的三相Buck整流器实验样机，如图19所示。实验样机主控芯片采用Microchip dsPIC33EP64GS505，主电路功率二极管采用IPD60R180P7，主电路功率MOSFET采用IDD08SG60CXTMA2。实验中用到的实验设备包括三相交流源、功率分析仪、示波器、多功能电能表等。

图19 三相Buck整流器实验平台

图20给出了半载（500 W）和满载（1 000 W）情况下传统不对称调制1和传统对称调制1的三相Buck整流器输入电流实验结果。对比图20a和图20c，以及图20b和图20d可知，传统不对称调制1和传统对称调制1的三相Buck整流器的输入电流在一个输入周期内均在相同位置存在六处扇区切换点畸变。传统不对称调制1半载时输入电流THD= 4.6%，满载时为3.8%；而传统对称调制1半载时输入电流THD=2.1%，满载时为1.5%。因此，在半载和满载下，传统对称调制1的输入电流谐波含量较低。

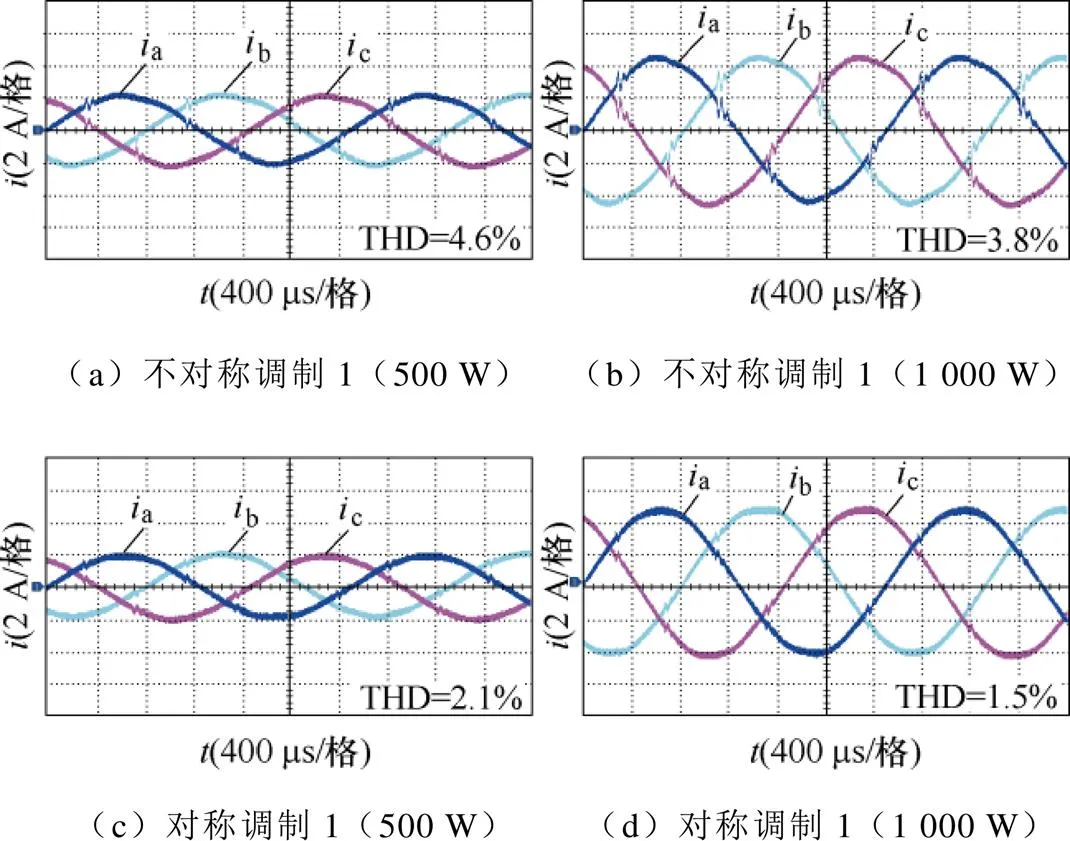
图20 传统调制的输入电流实验结果

图21给出了本文提出的不对称调制三相Buck整流器的输入电流实验结果。由图21a可知，三相输入电流在一个输入周期内不存在扇区切换点畸变，本文提出的不对称调制在半载时输入电流THD为1.7%，在满载时的输入电流THD仅为1.2%，输入电流THD较传统调制更优。

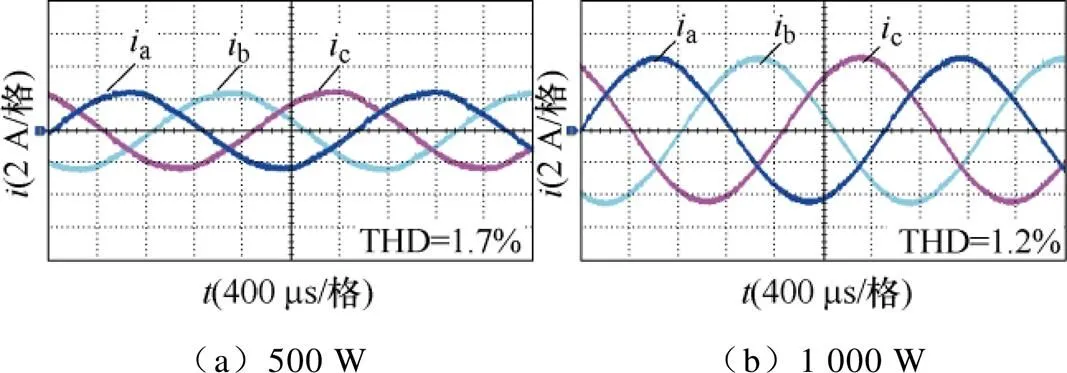
图21 提出调制的输入电流实验结果

图22给出了轻载时采用传统调制和本文提出的不对称调制策略的三相Buck整流器输入电流的各次谐波成分的实验结果。由图22可知，相较于传统调制策略，本文提出的不对称调制策略在轻载时的输入电流谐波含量明显减小。

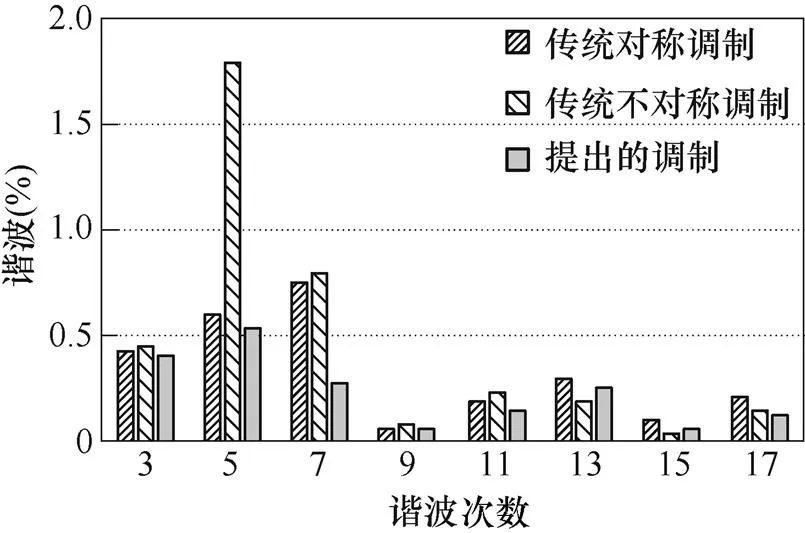
图22 输入电流谐波成分实验结果

图23给出了不同负载时采用传统调制和提出的不对称调制的三相Buck整流器的输入电流THD实验结果，由图23可知，20%～100%额定负载范围内本文提出调制的输入电流THD均优于传统 调制。

由图16～图18和图20～图23可知，实验结果与仿真结果一致，进而验证了本文分析结果的正确性。图20和图21证明了在全负载范围内，相较于传统调制策略，本文提出的不对称调制显著降低了输入电流THD。

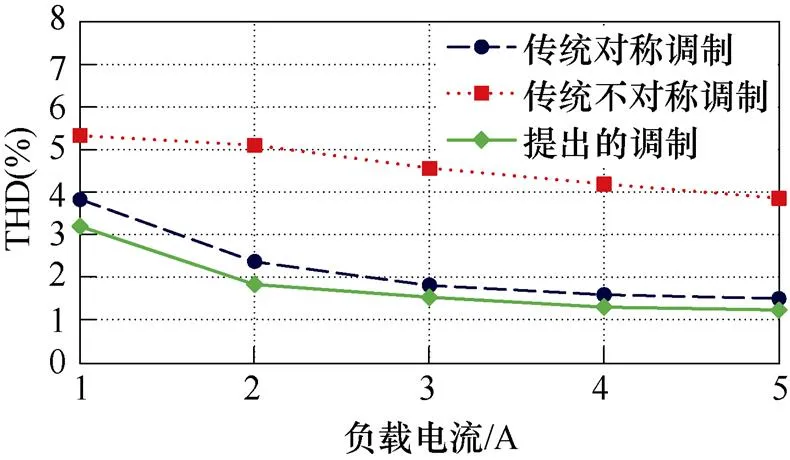
图23 输入电流THD实验结果

6 结论

首先，本文通过分析三相Buck整流器的直流链电流纹波对输入电流的影响，证明了传统对称调制相较于传统不对称调制拥有更优的输入电流质量。其次，通过分析扇区切换点处的驱动信号波形过渡过程，解释了传统调制中存在的输入电流扇区切换点畸变问题。最后，提出一种不对称调制策略，该调制策略保留了传统对称调制输入电流THD低的优点，并通过对PWM序列的优化排序，消除了存在于传统调制的输入电流扇区切换点畸变。因此，相较于传统调制，提出的不对称调制策略可以实现更优的输入电流THD。仿真和实验验证了所提出调制策略的可行性和有效性。

[1] 秦海鸿, 张鑫, 朱梓悦, 等. 电流型PWM整流器叠流时间对网侧电流影响及其抑制方法[J]. 电工技术学报, 2016, 31(12): 142-152.

Qin Haihong, Zhang Xin, Zhu Ziyue, et al. Influence of overlap time on the AC grid current of current source PWM rectifier and restraining method[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 142-152.

[2] 郭强, 刘和平, 彭东林, 等. 静止坐标系下电流型PWM整流器电流环控制策略研究及其参数设计[J]. 中国电机工程学报, 2014, 34(15): 2353-2361.

Guo Qiang, Liu Heping, Peng Donglin, et al. A novel control strategy and its parameter design of the current-loop in a stationary frame for current-source PWM rectifiers[J]. Proceedings of the CSEE, 2014, 34(15): 2353-2361.

[3] 易永仙, 张宇, 李民英, 等. 电流源型PWM整流器带容性负载的解耦控制方法[J]. 电工技术学报, 2016, 31(4): 95-103.

Yi Yongxian, Zhang Yu, Li Minying, et al. Decoupling control method of current-source PWM rectifier with capacitive load[J]. Transactions of China Electro- technical Society, 2016, 31(4): 95-103.

[4] 张强, 吴延飞, 张保顺, 等. 基于三相电流型五电平整流器的空间矢量脉宽调制算法[J]. 电工技术学报, 2020, 35(24): 5134-5141.

Zhang Qiang, Wu Yanfei, Zhang Baoshun, et al. Space vector pulse width modulation strategy based on three-phase five-level current source rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5134-5141.

[5] Kolar J W. Friedli T. The essence of three-phase PFC rectifier systems-part Ⅰ[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 176-198.

[6] Liu Pengcheng, Wang Zheng, Xu Yang, et al. Optimal overlap-time distribution of space vector modulation for current-source rectifier[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 4586-4597

[7] Benzaquen J, Fateh F, Shadmand M B, et al. Per- formance comparison of active rectifier control schemes in more electric aircraft applications[J]. IEEE Transactions on Transportation Electrification, 2019, 5(4): 1470-1479.

[8] Chen Qiang, Xu Jianping, Tao Zhuangyi, et al. Analysis of sector update delay and its effect on digital control three-phase six-switch Buck PFC converters with wide AC input frequency[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 931-946.

[9] Lei Jiaxing, Feng Shuang, Zhao Jianfeng, et al. An improved three-phase Buck rectifier topology with reduced voltage stress on transistors[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 2458-2466.

[10] 郭强, 刘和平, 彭东林, 等. 一种考虑电池自身特性的电流源型充电系统[J]. 电工技术学报, 2016, 31(16): 16-25.

Guo Qiang, Liu Heping, Peng Donglin, et al. A current-source charging system considering the characteristics of battery[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 16-25.

[11] Xu Fan, Guo Ben, Tolbert L M, et al. An all-SiC three-phase Buck rectifier for high-efficiency data center power supplies[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2662-2673.

[12] Xu Fan, Guo Ben, Xu Zhuxian, et al. Paralleled three-phase current-source rectifiers for high- efficiency power supply applications[J]. IEEE Transa- ctions on Industry Applications, 2015, 51(3): 2388- 2397.

[13] 郭强, 刘和平, 彭东林, 等. 电流型PWM整流器多环控制策略及其参数设计[J]. 中国电机工程学报, 2015, 35(5): 1193-1202.

Guo Qiang, Liu Heping, Peng Donglin, et al. Multi loop control strategy and parameter design of current source PWM rectifier[J]. Proceedings of the CSEE, 2015, 35(5): 1193-1202.

[14] 郭强, 周琛力, 李山. 面向电流源型PWM整流器直流侧电压的多环路控制策略[J]. 电工技术学报, 2022, 37(8): 2051-2063.

Guo Qiang, Zhou Chenli, Li Shan. A multiple loops control strategy based on DC link voltage of current source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2051-2063.

[15] Chen Qiang, Xu Jianping, Huang Rui, et al. A digital control strategy with simple transfer matrix for three-phase Buck rectifier under unbalanced AC input conditions[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(4): 3661-3666.

[16] Chen Qiang, Xu Jianping, Wang Lei, et al. Analysis and improvement of the effect of distributed parasitic capacitance on high-frequency high-density three- phase Buck rectifier[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6415-6428.

[17] Liu Pengcheng, Wang Zheng, Xu Yang, et al. Improved harmonic profile for high-power PWM current-source converters with modified space-vector modulation schemes[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11234-11244.

[18] Nussbaumer T, Kolar J W. Improving mains current quality for three-phase three-switch Buck-type PWM rectifiers[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 967-973.

[19] Guo Xiaoqiang, Yang Yong, Wang Baocheng, et al. Generalized space vector modulation for current source converter in continuous and discontinuous current modes[J]. IEEE Transactions on Industrial Electronics, 2020, 67(11): 9348-9357.

[20] 肖蕙蕙, 周琛力, 郭强, 等. 用于改善直流链电流纹波的电流源型整流器扇区优化调制策略[J]. 电工技术学报, 2021, 36(24): 5250-5260.

Xiao Huihui, Zhou Chenli, Guo Qiang, et al. Optimized sector modulation strategy of current source rectifier for DC-link current ripple redu- ction[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5250-5260.

[21] 郭小强, 杨勇, 王学惠. 电流源变换器直流链电流纹波抑制策略研究[J]. 中国电机工程学报, 2018, 38(20): 6071-6078.

Guo Xiaoqiang, Yang Yong, Wang Xuehui. Research on DC-link current ripple reduction for current source converter[J]. Proceedings of the CSEE, 2018, 38(20): 6071-6078.

[22] Guo Ben, Xu Fan, Zhang Zheyu, et al. Compensation of input current distortion in three-phase Buck rectifiers[C]//IEEE Applied Power Electronics Con- ference and Exposition, Long Beach, 2013: 930- 938.

[23] Baumann M, Nussbaumer T, Kolar J W. Comparative evaluation of modulation methods of a three-phase Buck+ Boost PWM rectifier-part Ⅰ: theoretical analysis[J]. IET Power Electronics, 2008, 1(2): 255-267.

An Asymmetric Modulation Strategy for Three-Phase Buck Rectifier with Low Input Current Total Harmonic Distortion

（Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle Ministry of Education School of Electrical Engineering Southwest Jiaotong University Chengdu 610031 China）

The input current total harmonic distortion (THD) is an important performance indicator of a three-phase Buck rectifier, closely related to the modulation strategy. When calculating the dwell time of the vector in the previous research on space vector pulse-width modulation (SVPWM), the ripple of the DC-link current was ignored, i.e., it was considered a constant value. However, in practical applications, to improve dynamic performance and power density, the output inductor of the three-phase Buck rectifier takes a small value, which leads to a large DC-link current ripple. In this case, the impact of the DC-link current ripple on the input current becomes obvious. Secondly, the input current of the three-phase Buck rectifier with the conventional SVPWM modulation strategies has severe distortion during the sector transition. Therefore, this paper proposes a low input current THD modulation strategy, which considers the influence of DC-link current ripple on the input current quality and eliminates the input current distortion during the sector transition. Therefore, the input current THD is effectively reduced.

The impact of the DC-link current ripple on the input current is analyzed in this paper. Firstly, based on the operating states of the three-phase Buck rectifier in sector 1, the relationship between the input current of the three-phase bridge arm and the DC-link current is obtained. Secondly, the relationship between the input average equivalent current amplitude of the three-phase bridge legs is analyzed for different modulation strategies. Then, the amplitude relation between the input voltage and the corresponding input current is obtained. When the ripple of the DC-link current is large, the results show that the ratio of the three-phase input current to the corresponding input voltage is not equal to the conventional asymmetric modulation, which leads to a high harmonic content in the input current. For the conventional symmetric modulation, the ratio of the three-phase input current to the corresponding input voltage is equal, which means that the harmonic content of the input current is lower than the conventional asymmetric modulation.

In addition, the paper also analyzes the reason for the input current distortion during the sector transition of the conventional SVPWM modulation strategies. The relation between the three-phase input current and dc-link inductor current is given, the input inductor current of each vector is deduced, and the transition process of drive signals with different modulation strategies during the sector transition is given. The analysis shows that the input current of the conventional SVPWM modulation strategies has distortion during the sector transition.

A low input current THD modulation strategy is proposed. In this modulation scheme, the influence of the output inductor current ripple on the input current is considered, and the input current distortion during the sector transition is eliminated. The simulation results show that among the three modulations, the input current THD of the conventional asymmetric modulation is the highest (4.9%), and the input current THD of the conventional symmetric modulation is lower (2.3%) than that of the conventional asymmetric modulation. The input current THD of the proposed low input current THD modulation strategy is only 1.7% at half load and 1.2% at full load, respectively, which is the lowest among the three modulation strategies.

Three phase Buck rectifier, ripple of the DC-link current, input current distortion, asymmetric modulation strategy

国家自然基金资助项目（61733015）。

2023-01-18

2023-04-20

10.19595/j.cnki.1000-6753.tces.230074

TM461

曹海彬 男，1999年生，硕士，研究方向为电力电子功率变换器的调制与控制方法。E-mail: Caohaibin@my.swjtu.edu.cn

许建平 男，1963年生，教授，博士生导师，研究方向为电力电子数字控制技术、开关电源新颖控制技术、再生能源发电技术、移动信息设备电源管理技术等研究。E-mail: jpxu-swjtu@163.com（通信作者）

（编辑 陈 诚）