钻井法凿井气-液-固耦合排渣流场及刀盘吸渣口优化

程 桦 ， 郭龙辉 ， 姚直书 ， 杨 光 ， 荣传新

(1.安徽理工大学 土木建筑学院, 安徽 淮南 232001；2.安徽建筑大学 建筑结构与地下工程安徽省重点实验室, 安徽 合肥 230601；3.中煤特殊凿井有限责任公司, 安徽 合肥 230001)

我国西部矿区煤炭多赋存于白垩—侏罗系含水弱胶结岩石地层，新井建设常采用冻结法施工深大立井井筒[1-3]。与冻结法相比，钻井法凿井具有机械化程度高、作业环境好、井壁质量高等优点，符合少人、安全、绿色、智能化的煤炭行业发展趋势[4-7]。长期以来，钻井法主要应用于中东部地区深厚松散层立井施工，将该工法应用于西部可可盖煤矿含水弱胶结岩石地层进、回风井深大立井施工在国内外尚属首次[8-9]。但在钻进侏罗系泥岩、泥质砂岩等含泥地层时，出现了泥浆突变、刀具磨损严重、钻进效率低等工程问题[10-11]。初步分析表明，对气-液-固耦合排渣流场缺乏认识，现行吸渣口设计与洗井参数无法适应该类地层高效钻进要求，是导致钻进排渣效率低的主要原因之一，亟待研究解决。

国内外相关领域的专家学者，针对洗井排渣流场、钻头吸渣口布置、排渣参数优化等问题，开展了大量研究，取得了系列成果。在排渣流场研究方面，伍晓龙[12]等对气举反循环双壁钻具环形空间及气水混合器流场中的速度及压力进行了仿真分析，发现减少双壁钻杆环形空间的变径有利于减少压力损失和能量损耗，且对称进气孔结构更利于上返速度的均匀性；夏敏等[13]通过数值模拟研究了大直径有、无牙轮钻头钻进时井底流场速度分布规律，认为距吸渣口较远处易产生岩屑堆积，可通过增大泥浆流量减小沉积区。但上述气举反循环流场的研究还处于数值模拟方面的可行性探讨，缺乏室内试验验证，且与工程应用尚有距离。

在刀盘吸渣口优化研究方面，前苏联曾在顿巴斯采用YZTM-8.75 型钻机开展吸渣口优化的现场试验，发现三吸渣口布置，泥浆的压头损失严重且易发生堵塞，单吸渣口的抽吸速度及冲开能力均较三吸渣口强；美国和日本曾采用机械方式在钻头上安装刮板或刀具泵，使剥离的钻渣直接刮、吸向吸渣口[14]；黄志强等[15]改变了潜孔钻头排屑槽的布置方式，将径向布置改为切向布置，此举减小了井底流体的旋涡强度，改善了排渣效果；付孟雄[16]针对现有两翼PDC 钻头设计的不足，改进了钻头排渣口的位置和排渣通道尺寸，大幅减小了排渣流场钻渣聚集区，提高了排渣效率。可见，国内外在该方面的研究仅局限于工程试验，缺乏理论指导，且所做的工作已年代久远。

在钻井排渣施工影响因素方面，国外学者S WALKER[17]研究了钻渣粒度、洗井液流变性等对连续水平油管钻进作业时井底钻渣输送的影响，发现洗井效果受限于钻渣尺寸和洗井液黏度，湍流状态下的低黏流体洗井效果更好；刘少伟[18]、易振华[19]、熊亮[20]等分别开展了巷道底板锚固孔、灌注桩孔和瓦斯抽排井的反循环钻进排渣参数研究，认为影响排渣效果的主要因素有：进水孔和排渣通道孔径、泥浆循环量、注气量、注气压力等，并提出了合理的排渣参数组合。但钻井法施工灌注桩、瓦斯抽排井和油气井，在钻井工艺、钻井直径、排渣方式、排渣流型等方面均与矿山立井钻井法凿井存在较大区别，相关成果无法满足需要。

综上，笔者以西部地区可可盖煤矿中央回风立井ϕ4.2 m 超前钻井为研究背景，基于CFD-DEM 方法，建立气-液-固多相耦合排渣数值模型，分析其排渣流场分布规律及主要影响因素；提出优化刀盘吸渣口评判指标和方法，优化吸渣口布置方式和相关参数，为优化吸渣口布置，选择合理钻进参数，提高排渣与钻进效率提供理论参考。

1 气举反循环排渣数值模型

1.1 工程背景

可可盖煤矿位于陕西省榆林市境内，设计生产能力为10 Mt/a，煤层赋存地层为西部典型的富水弱胶结岩石地层，矿井开拓采用敞开式TBM 掘进主、副斜井和钻井法施工中央进、回风井的联合方式，其中，中央进、回风立井是我国在西部地区首次采用钻井法施工的立井井筒且在近期均已成功完成了钻进工作[21]。

中央回风立井井筒设计深度521.5 m，净直径6 m，井筒依次下穿第四系、白垩系、侏罗系地层，井筒钻进荒径为8.5 m，钻进方式选用AD130/1000 型全液压动力头竖井钻机(图1)进行ϕ4.2 m 超前钻进和ϕ8.5 m扩孔钻进联合的两级钻进施工，其中超前钻孔采用直径为4.2 m 的平底滚刀钻头，滚刀布置采用14 把正刀+4 把边刀+1 把中心刀的组合方式，钻头吸渣口采用中心式+偏心扫掠式双吸渣口布置方式(图2)，洗井方式采用气举反循环泥浆悬浮排渣工艺。

图1 AD130/1000 型竖井钻机Fig.1 AD130/1000 shaft drilling rig

1.2 多相耦合排渣数值模型

为研究气-液-固三相耦合排渣流场分布规律，采用CFD-DEM 方法，建立气举反循环排渣数值模型，其中流体相泥浆和压缩空气的计算在流体仿真软件Fluent 中进行，离散相岩渣颗粒在离散元仿真软件EDEM 中进行，2 者通过编译UDF 耦合接口实现耦合计算。

1.2.1 控制方程

(1)流体相控制方程。气举反循环排渣过程是压缩空气-泥浆-岩渣三相耦合的流动，在流体仿真软件Fluent 中选择欧拉多相流模型对流体相进行仿真分析，考虑到泥浆满足非牛顿流体流变特性，因此选择幂律流体模型；为提高欧拉多相流的计算精度，选择标准k-ε湍流模型计算排渣流场。排渣流场中泥浆与空气的运动满足流体质量守恒和牛顿第二定律，因此在欧拉坐标系中建立混合流体的连续方程和动量守恒方程[22]，分别为

式中，i表示液相或气相；αi、ρi、vi分别为i相的体积分数(%)、密度(kg/m3)、速度(m/s)； τi为i相的应力-应变张量；P、Fi、Flift,i、Fvm,i、Fwl,i、Ftd,i、R分别为相间共享压力、外部体积力、升力、虚拟质量力、壁面力、相间湍流扩散力和相间相互作用力。

(2)离散相的控制方程。选用EDEM 离散元仿真软件对排渣流场中岩渣的运移过程进行仿真分析，在井底生成30 000 个直径为3 mm 的球形颗粒用以模拟岩渣[10]，并选择Hertz-Mindlin 无滑移弹性接触模型模拟岩渣颗粒间的碰撞和挤压，每个岩渣颗粒在运动过程中满足牛顿第二定律和动量守恒方程[23-24]，即

式中，m为岩渣的质量，kg；v为岩渣的运移速度，m/s；ρl为流体密度，kg/m3；ρ为岩渣密度，kg/m3；FD分别为岩屑受到的牛顿阻力；FC为岩屑与其他岩屑以及壁面接触的合力。

岩屑颗粒的角动量守恒方程为

式中，I为岩渣颗粒的转动惯量，kg·m2；ω为角加速度，rad/s2；Tq、Tc、Tz分别为岩渣颗粒所受的切向、法向和轴向扭矩，N·m。

1.2.2 反循环排渣数值模型建立

结合钻井法凿井气举反循环排渣施工工艺和ϕ4.2 m 超前钻头的结构形式、吸渣口布置、刀具布置(图2)，建立了气举反循环排渣的缩尺数值模型(为现场实际模型的1/12)，如图3 所示。数值模型主要包括井底、钻头和排渣管，将井底和排渣管设置为流体域，钻头设置为旋转域，以四面体网格划分模型，并对钻头和注气口进行局部网格加密，共计划分91 064 节点、441 661 网格。在Fluent 中依次设置欧拉多相流模型、标准k-ε湍流模型计算流场，并定义泥浆和空气的材料属性(表1)、边界条件(空气以8.4 m3/h 输入，泥浆以0.03 MPa 压力输入)和旋转域属性(以30 r/min绕z 轴旋转)；在EDEM 中设置岩渣属性参数并生成3 万个球形岩渣颗粒，使刀具钻入岩渣3 mm，经耦合接口连接Fluent 和EDEM 进行流体相和离散相的数值分析计算。其计算流程如图4 所示，建模参数见表1，建模参数由现场实际施工参数和相似准则转化得到，相似准则推导见文献[10]。

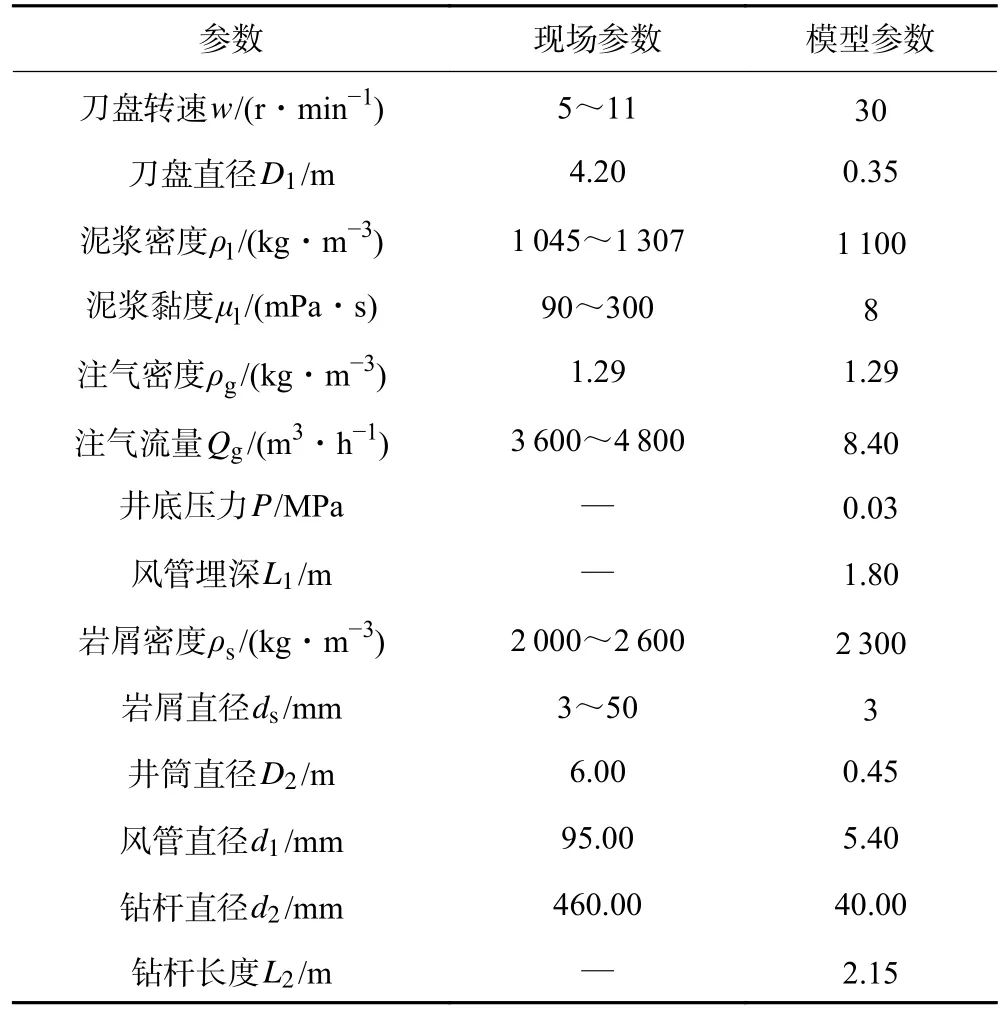
表1 建模参数选取Table 1 Selection of modeling parameters

图3 排渣数值模型及网格划分Fig.3 Numerical model and grid division of slag discharge

图4 数值模型计算流程Fig.4 Calculation flow of numerical model

2 排渣流场分布规律

为分析井底工作面和排渣管内的流场分布规律，在数值模型z=0.2、1.5 m 两截面上分别设置排渣管水平测线H1和H2，在x=0 截面处设置垂直测线V1；在井底z=-0.22 m 截面上设置两条水平测线L1和L2，在刀盘井底设置9 条垂直测线(吸渣口处的S1、S2，钻头径向的S3～S5，滚刀周边的S6～S9)，测线布置如图5所示。数值分析计算参数见表1。

图5 排渣流场测线布置Fig.5 Layout of measuring line for slag discharge flow field

2.1 排渣管内流场

图6(a)～(c)为V1测线上的速度及压力分布图，图6(d)～(f)为H1/H2测线上的速度及压力分布图。

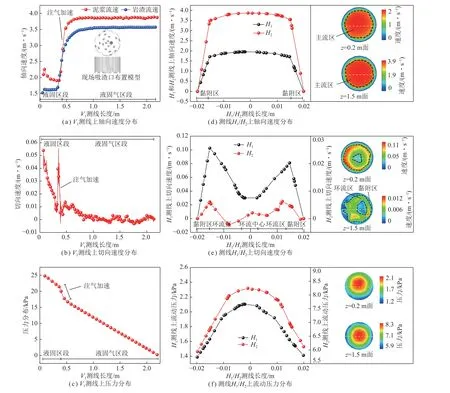
图6 排渣管内V1 和H1/H2 测线上的速度及压力分布Fig.6 Velocity and pressure distribution on V1 and H1/H2 measuring lines in the slag discharge pipe

分析图6(a)～(c)可知，排渣管内液固气区段泥浆及岩渣的轴向速度远大于液固区段，岩渣和泥浆途经注气端时，上返速度分别大幅提升116%和99%，排渣管内泥浆的上返速度始终大于岩渣，其中在液固、液固气区段，泥浆的平均上返流速较岩渣分别增长23.9%和9.8%；泥浆的切向速度反映其环流程度，在钻头转动影响下，排渣管内液固区段泥浆环流现象显著，但在液固气区段泥浆的高速上返大大削弱了其切向运动，环流现象逐渐消失，流场更利于排渣[25]；当压缩空气输入排渣管，管内混合流体的密度及压力骤然降低，在外部泥浆柱压力作用下，泥浆及岩渣实现“注气加速”，获得高流速而被举升。

分析图6(d)～(f)可知，沿排渣管断面，H2测线上平均轴向速度较H1测线增大2 倍，但切向速度则降低27 倍，两测线上流体轴向速度均远大于其切向速度，因此排渣管内流体的运动以轴向流动为主，且高速流动的泥浆流主要分布在排渣管中心区域的主流区内，近排渣管内壁面处(黏附区)，泥浆流速则因黏滞阻力而迅速降低(图6(d))；泥浆的切向运动沿排渣管断面自内向外可划分为环流中心、环流区和黏附区，其切向流速在环流中心处较小，在环流区随管径的增加而增大，在黏附区随管径的增加而减小(图6(e))；排渣管内流体的流动压力变化反映其动能变化，管内两水平测线动能分布均呈抛物线型，中心处动能最大并向两侧逐渐递减(图6(f))。

2.2 井底流场

本节通过分析刀盘水平测线L1、L2和垂直测线S1～S9上的速度及压力分布来研究井底流场的分布规律。

井底水平测线上流场分布如图7 所示，分析图7可见，井底泥浆的轴向上返主要集中在吸渣口附近，扫掠吸渣口处泥浆的上返速度较中心吸渣口处增大35.4%，因此扫掠吸渣口的吸附力较中心吸渣口更强；井底泥浆的运动形式以水平切向流动为主，以L2 测线为例，其平均切向流速约是轴向流速的15 倍，是径向流速的2 倍，钻头中心处泥浆切向速度最小，沿钻头半径向外逐渐增大，泥浆的径向运动仅发生在吸渣口两侧，远离吸渣口处，泥浆的径向速度较小，对岩渣的冲刷及携带能力较弱，因此易发生岩屑堆积；井底压力分布沿径向自外向内近似呈线性降低，在吸渣口处压力值最小，且扫掠吸渣口处较中心吸渣口更小，此时环空泥浆柱与井底的压差就越大，井底泥浆与岩渣更易被吸附举升。

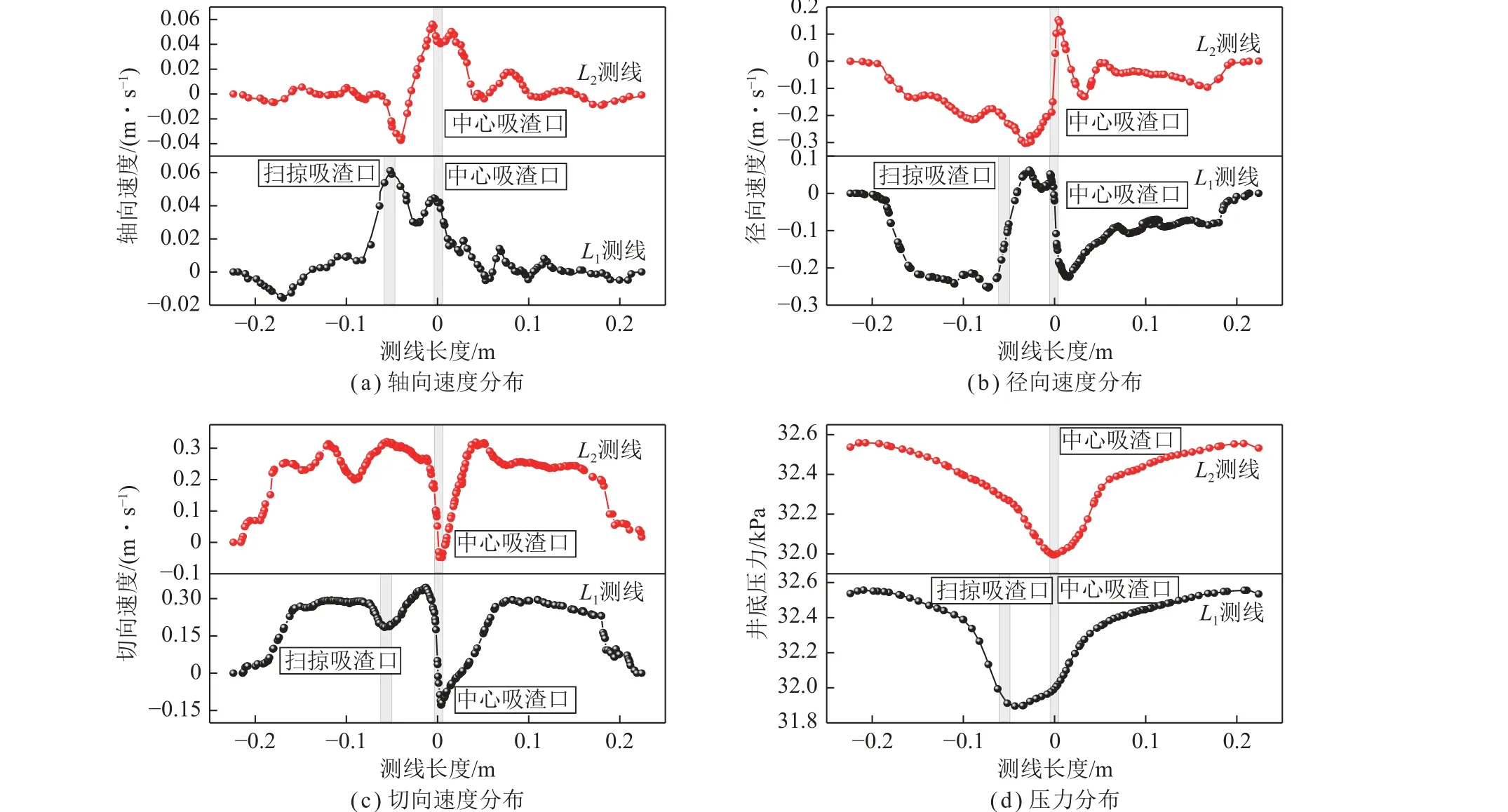
图7 井底水平测线L1 和L2 上速度与压力分布Fig.7 Velocity and pressure distribution on L1/L2 bottom hole horizontal survey line

井底净空垂直方向吸渣口处S1/S2测线流场分布如图8 所示，井底径向S3～S5测线流场分布如图9 所示，钻头周边S6～S9测线流场分布如图10 所示。

图8 吸渣口处S1 和S2 测线上速度与压力分布Fig.8 Velocity and pressure distribution on S1/S2 measuring line at slag suction port

图9 井底径向S3～S5 测线上速度与压力分布Fig.9 Velocity and pressure distribution on bottom hole radial S3-S5 survey line

图10 钻头周边S6～S9 测线上速度与压力分布Fig.10 Velocity and pressure distribution on S6-S9 survey line around the drill bit

分析图8 可知，吸渣口吸附区域内，泥浆的流动以轴向上返为主，且中心吸渣口处平均轴向速度分别较径向、切向速度增大8 倍和14 倍，扫掠吸渣口处分别增大4 倍和2 倍；中心吸渣口和扫掠吸渣口处泥浆的轴向速度沿井深方向近似呈线性增大，且中心吸渣口处增速略大，但泥浆的切向、径向速度均较扫掠吸渣口处显著降低；井底每一净空深度扫掠吸渣口处井压均小于中心吸渣口，表明扫掠吸渣口处与环空泥浆柱之间的压差更大，泥浆和岩渣更易被吸附举升。

分析图9 可知，沿井底径向布置的垂直测线上泥浆的轴向、径向速度在破岩面和钻头底面都趋近于0，轴向速度近似在井底净空中心处达到最大，且在吸渣口吸附作用下，泥浆的轴向、径向速度均随钻头半径的减小而增大，距离吸渣口较远处，泥浆几乎不发生轴向运动；贴近钻头表面处(距井底20～25 mm)，泥浆随钻头做同向运动，其环流程度随旋转半径的增大而增大，在距井底10～20 mm 内，钻头对泥浆的拖曳作用等同于其黏滞阻力，泥浆近似以恒定速度环向运动，在距井底10 mm 内，泥浆的黏滞力起主导作用，其切向速度随距井底距离的减小而减小，直至为0[13]；在井底水平同一净空深度，井压沿着钻头边缘向中心方向均匀递减，在钻头表面至井底的垂直方向上，井压呈线性增加，且不同径向位置的井压增速近似相等。

分析图10 可知，由于钻头在钻进过程中，刀具对井底泥浆具有推动作用，钻头刀具周边泥浆的轴向速度与切向速度，均在迎头处大于尾部，外侧大于内侧(图11)。此外，刀具划过井底，在其外侧及尾部形成涡旋，导致泥浆流向时上时下；刀具周边泥浆径向流速迎头处大于尾部，内侧略大于外侧，且外侧泥浆在距井底20～25 mm 内流向发生改变，流向背离吸渣口方向，因此刀具对其外侧泥浆流的径向运动具有一定的阻滞作用；同一井底净空深度，刀具内侧压力小于外侧，刀具前、后压力分布并无显著差异。

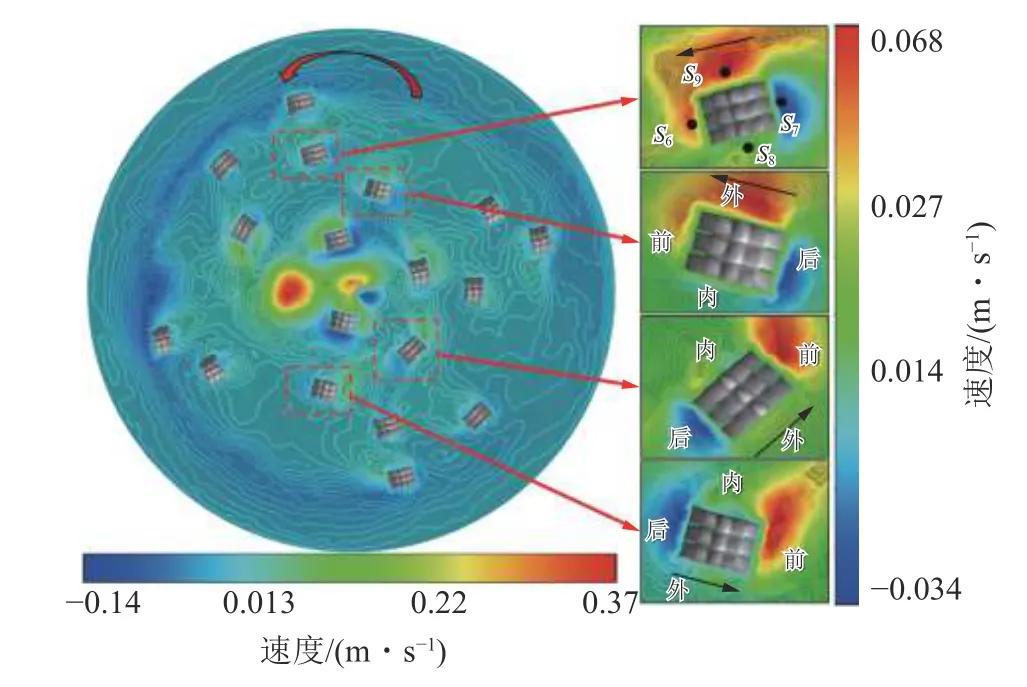
图11 钻头刀具周边流体轴向速度分布云图Fig.11 Cloud image of axial velocity distribution of fluid around the bit cutter

2.3 岩渣的分布与运移

基于现场排渣数值模型，选取不同时刻井底及排渣管内岩渣的分布状态，分析其汇聚、悬浮、吸附、举升等运移规律。

分析图12 可知，岩渣在井底做“汇聚—悬浮—吸附—举升”运移，首先，岩渣在吸附作用和钻头、旋转泥浆流的推动作用下逐渐汇聚井底中部，其次，旋转泥浆流增大对岩渣的扰动力，使其克服泥浆柱的压持效应而悬浮井底，并在吸渣口吸附作用下抽排出井底进入排渣管，岩渣运移循环往复，直至井底彻底清零；泥浆携带岩渣途经注气端，在气举和压差作用下上返速度大幅增加，但由于气相输入，岩渣的密度分布显著降低，因此，岩渣以高返速、低密度的形式在排渣管内运移，直至排出地面。

图12 井底及排渣管内岩渣的分布状态Fig.12 Distribution of rock slag in bottom hole and slag discharge pipe

3 刀盘吸渣口优化

3.1 优化内容及评价指标

煤矿立井钻井法施工过程中，井底部分岩渣因吸渣口布置不合理等原因积聚井底被重复破碎，致使钻头磨损增大，钻进效率降低[26]。因此，本节以可可盖煤矿中央回风立井ϕ4.2 m 超前钻进为背景，取清渣率η、泥浆输送比λ和气力输送比 ξ作为评判指标，从刀盘吸渣口的数量、间距、面积比和总面积4 个方面对吸渣口的布置进行优化，优化流程如图13 所示。

图13 钻头吸渣口优化流程Fig.13 Optimization flow chart of bit slag suction port

式中，Mtotal为生成岩渣的总质量；Ms为累计排出岩渣的质量；Ml为累计排出泥浆的质量；Mg为累计输入气体的质量。

3.2 吸渣口优化结果

定义两吸渣口中心距与钻头半径之比为长径比α，两吸渣口面积的比值为面积比β，两吸渣口总面积占钻头横截面积的百分比为总面积占比γ，按照图13 钻头优化流程，依次改变吸渣口的数量n(分别为1，2)，长径比α(分别为0.3，0.4，0.5)，面积比β(分别为1，0.5，0.25，0.17)，总面积占比γ(分别为1.63%，1.78%，1.94%，2.12%)，建立不同的钻头吸渣口布置数值模型(图14)，基于每次吸渣口优选结果逐级优化并选出最佳吸渣 口布置方式，计算结果见表2 和图15。

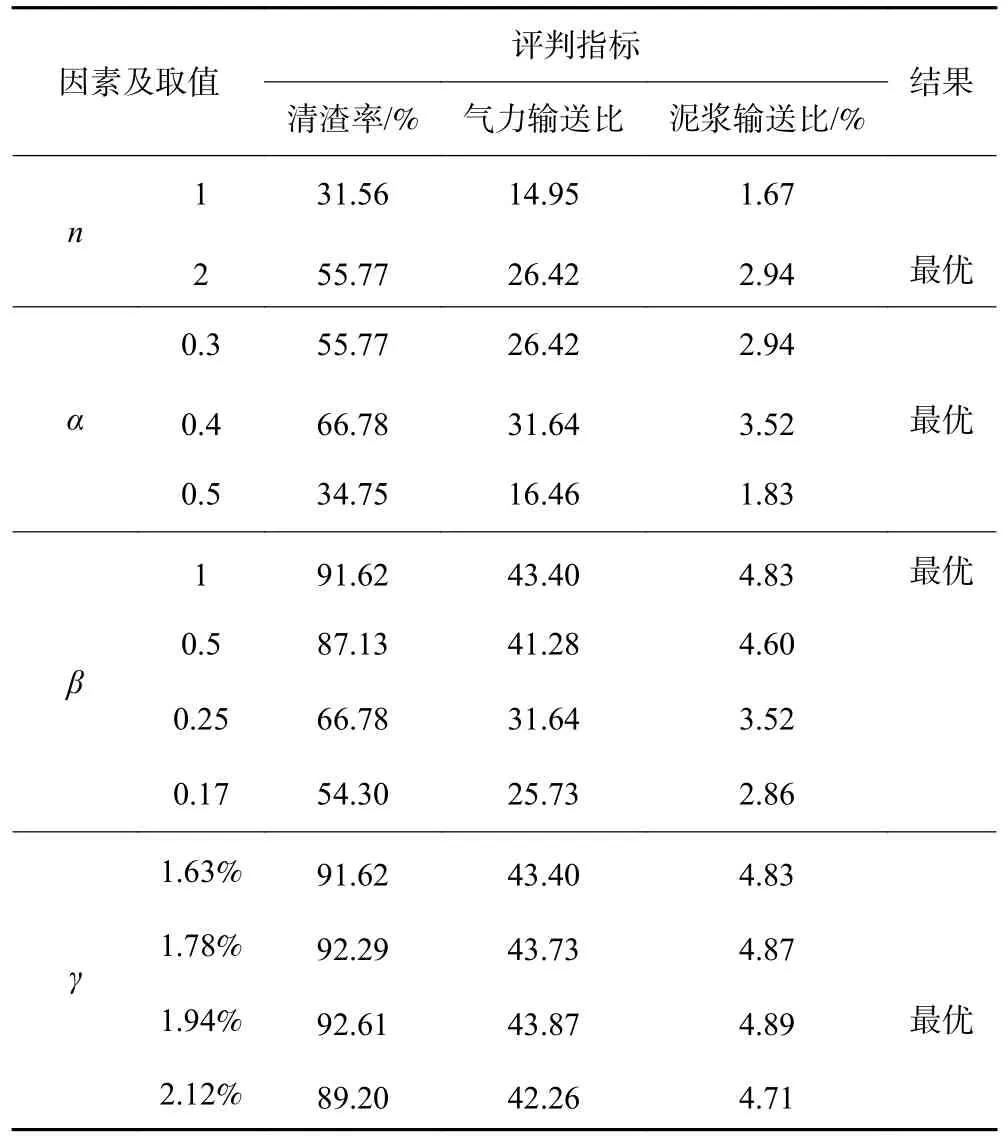
表2 吸渣口优化计算结果Table 2 Optimization calculation results of slag suction port

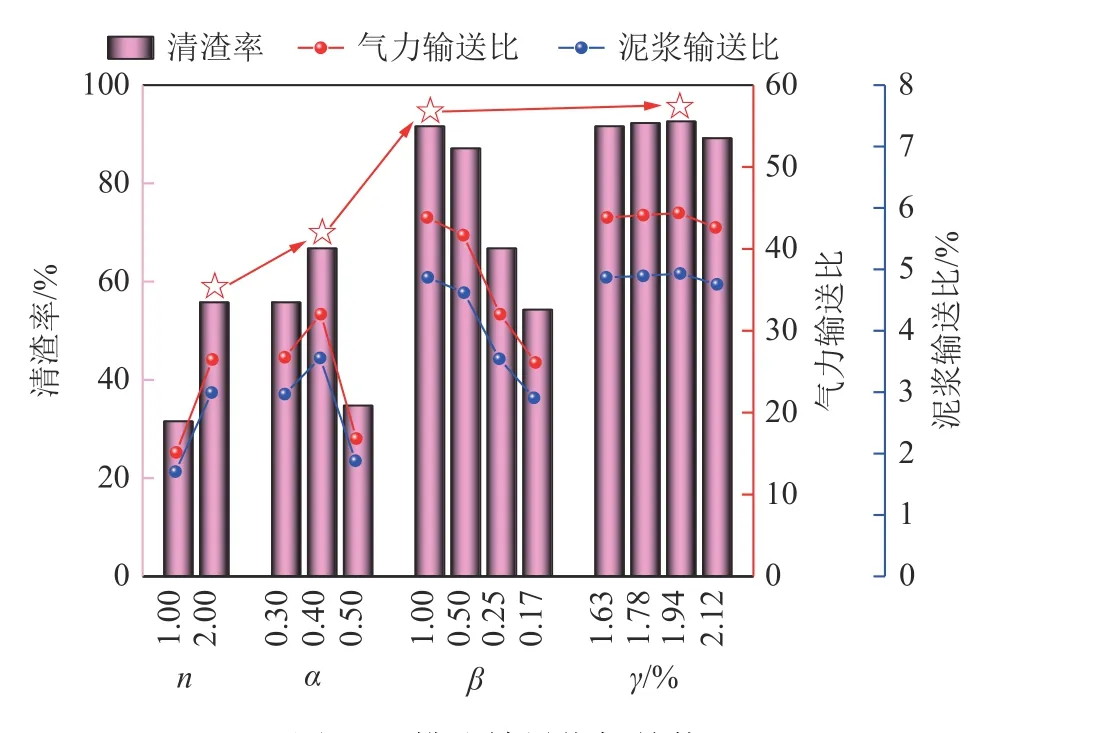
图15 排渣效果指标趋势Fig.15 Trend chart of slag discharge effect index

分析表2 和图15 可知：

(1)刀盘吸渣口总面积相同时，双吸渣口布置方式排渣效果较单吸渣口好。单吸渣口由于其偏心布置方式，在靠近吸渣口一侧出现井底泥浆径流短路现象，在井底中心位置及远离吸渣口一侧泥浆流速衰减严重，致使钻渣积聚井底中心无法被泥浆举升而重复破碎，严重影响排渣效果。双吸渣口布置方式具有分布均匀、吸附范围广的优点，且吸附兼顾井底中心和钻头外缘岩渣滞留区，因此，双吸渣口布置方式较为合理，且清渣率较单吸渣口布置增长76.5%，泥浆携岩能力及气力举升能力也显著提升。

(2)当两吸渣口间距过近时，吸附区域会发生交叉重叠造成有效吸附面积减小，当两吸渣口间距过大时，吸渣口之间存在“吸附空白区”，且外侧吸渣口因其线速度过大而造成吸附效果差，因此两吸渣口间距的布置并非越近或越远最好，其存在一最优阈值，且当吸渣口长径比α为0.4 时排渣效果最佳，其清渣率较现场双吸渣口布置方式提升19.7%。

(3)清渣率、气力输送比和泥浆输送比均随着吸渣口面积比β的增大而增大；井底岩渣暴露于扫掠吸渣口吸附路径下方的时间较短，扫掠吸渣口吸附能力有限，尚有大量岩渣滞留井底，且主要分布在中心部位，因此适当增大中心吸渣口面积有利于提高排渣效果，且当吸渣口面积比β为1 时，其清渣率较现场双吸渣口布置方式提升64.3%。

(4)在经历吸渣口的数量、长径比和面积比的优化后，排渣效果得到明显的改善，继续增大吸渣口的面积，清渣率及其他清渣指标均小幅增长后下跌，可见过度增大吸渣口的总面积反而会导致吸渣口吸附力不足而降低排渣效果，因此优选吸渣口总面积占比γ为1.94%，其清渣率较现场双吸渣口布置方式提升66.06%。

综上，通过建立13 个排渣数值模型，依次改变吸渣口的数量、间距、面积比和总面积，最终发现吸渣口的数量n为2，长径比α为0.4，面积比β为1，总面积占比γ为1.94%时吸渣口的布置方式最佳且排渣效果最好。

3.3 试验验证

为验证排渣流场分布数值模拟及优化吸渣口结果的正确性，采用自研的可视化气举反循环泥浆悬浮排渣试验装置(图16)，设计几何相似缩比为12 的相似模型试验，并利用高频摄像机对排渣管内岩渣进行监测捕捉，通过PIV 测试技术获取了排渣管流场中岩渣的上返速度，其中相似模型设计、试验装置研制和试验过程见文献[10]，试验参数选取同表1，图17 为试验与数值模拟结果对比。

图16 气举反循环排渣试验装置示意Fig.16 Schematic diagram of gas lift reverse circulation slag discharge test device

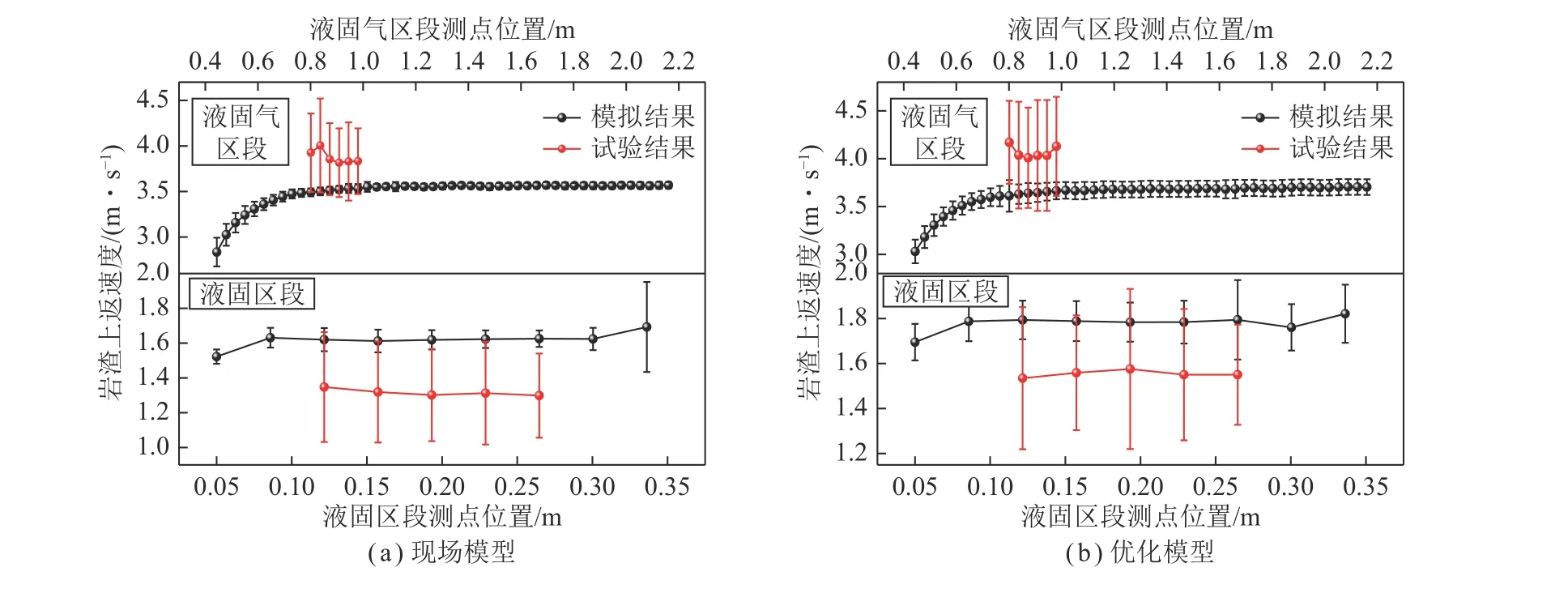
图17 试验与模拟流场岩渣上返速度对比Fig.17 Comparison of upward velocity of rock slag between experimental and simulated flow fields

模型试验结果显示，现场模型排渣管内液固及液固气区段岩渣平均上返速度分别为1.32 和3.88 m/s，对应优化模型为1.55 和4.07 m/s，优化模型排渣管内液固及液固气段岩渣上返速度较现场模型分别提升17.4%和4.9%；与数值模拟结果相比，现场模型排渣管内液固及液固气段岩渣上返速度相对误差分别为22.7%和10.9%，对应优化模型相对误差分别为14.8%和13.1%，试验结果与模拟结果具有较高的吻合性，从而验证了数值模拟排渣流场分布的正确性和优化吸渣口布置的优越性。

4 排渣流场影响因素分析

4.1 排渣管内流场主要影响因素

以排渣管内V1测线的速度及压力分布为例，分析钻头转速(20～40 r/min)，注气量(6.4～10.4 m3/h)，风管没入比(0.70～0.88)，泥浆黏度(1～11 mPa·s)等因素对优化模型排渣管内流场的影响。

分析图18～21 可知：

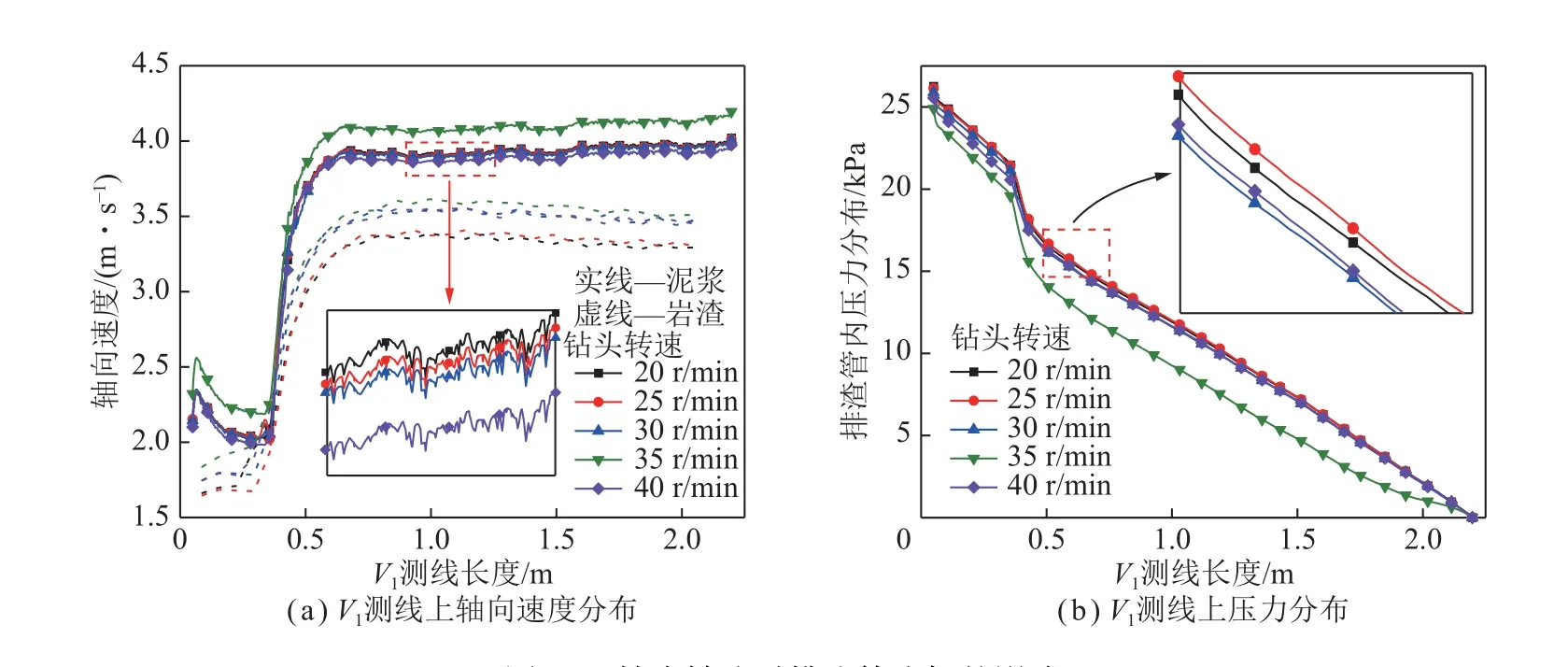
图18 钻头转速对排渣管流场的影响Fig.18 Influence of bit speed on flow field of slag discharge pipe

图19 注气量对排渣管流场的影响Fig.19 Influence of gas injection on flow field of slag discharge pipe

图20 风管没入比对排渣管流场的影响Fig.20 Influence of air duct submergence ratio on flow field of slag discharge pipe

图21 泥浆黏度对排渣管流场的影响Fig.21 Influence of mud viscosity on flow field of slag discharge pipe

(1)排渣管内泥浆及岩渣的上返速度随钻头转速的增加呈先增加后降低趋势，当转速为35 r/min 时，泥浆及岩渣的上返速度均达到峰值，分别较低转速20 r/min 时增加4.4%和7.2%，当转速增至40 r/min时，泥浆及岩渣的上返速度骤然降低，因此钻头转速存在最优阈值，在合理范围内增加钻头转速可小幅提高泥浆及岩渣的上返速度；排渣管内压力分布随转速的增加呈先减小后增加趋势，当转速为35 r/min 时，排渣管内压力最小，即排渣管内外泥浆柱的压力差最大，泥浆及岩渣更易获得高流速而被举升。

(2)增大注气量可以显著增加排渣管内液固气区段的气体体积分数及岩渣、泥浆的上返流速。当注气量从6.4 增至10.4 m3/h 时，排渣管内气体平均体积分数增长31%，液固气区段岩渣及泥浆的平均上返流速分别增长25%和27%，且排渣管内的压力随注气量的增加而降低。这是由于当注气量增加时，会以较大动能克服排渣管内混合流体重力势能而做功，压缩空气的动能向混合流体重力势能及动能转变，使其以高流速上返；另外，随着注气量增加，排渣管内混合流体的密度及压力迅速降低，在外部环空泥浆柱压差作用下，排渣管内混合流体更易获得高返速。

(3)增大风管没入比可使岩渣-泥浆两相流提前被“注气加速”，且在一定程度上可小幅增加排渣管内液固气段岩渣及泥浆的上返流速。当风管没入比从0.70 增至0.84，岩渣-泥浆两相流提前被加速，且分别实现8.9%、11.8%的增幅，多相流上返路径延长，但获取高流速上返，有效节省了岩渣及泥浆自井底至地面的流动时间[27]。

(4)泥浆黏度与混合流体的上返速度呈负相关关系。低密度、低黏度的泥浆更易获得高返速，且在排渣管内保持低压状态，但携岩能力较差。当泥浆黏度为1 mPa·s，密度为1 kg/m3时(此时泥浆为清水)，其上返流速为4.28 m/s，较黏度梯度为2～11 mPa·s 的泥浆(密度为1.1 kg/m3)分别增长6.7%～9.7%，岩渣颗粒上返流速分别增长6%～7%。这是因为低黏、低密度的泥浆与钻杆内壁间的壁面剪切力较小，沿程阻力损失少，在液固气区段易形成低密度的混合流体且保持管内低压状态，因此能获得高流速，但是在实际钻井工程中，还要考虑泥浆平衡地压、井帮护壁、悬浮井壁、携带岩渣的能力，因此泥浆黏度及密度也并非越小越好。

4.2 井底流场主要影响因素

以井底水平测线L1上的速度及压力分布为例，分析钻头转速(20～40 r/min)，注气量(6.4～10.4 m3/h)，风管没入比(0.70～0.88)，泥浆黏度(1～11 mPa·s)等因素对优化模型井底流场的影响。

图22～25 分别为钻头转速，注气量，风管没入比和泥浆黏度对井底L1测线上速度及压力分布的影响曲线，分析可得

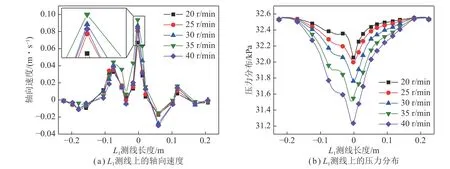
图22 钻头转速对L1 测线上速度及压力的影响Fig.22 Influence of bit speed on speed and pressure on L1 survey line

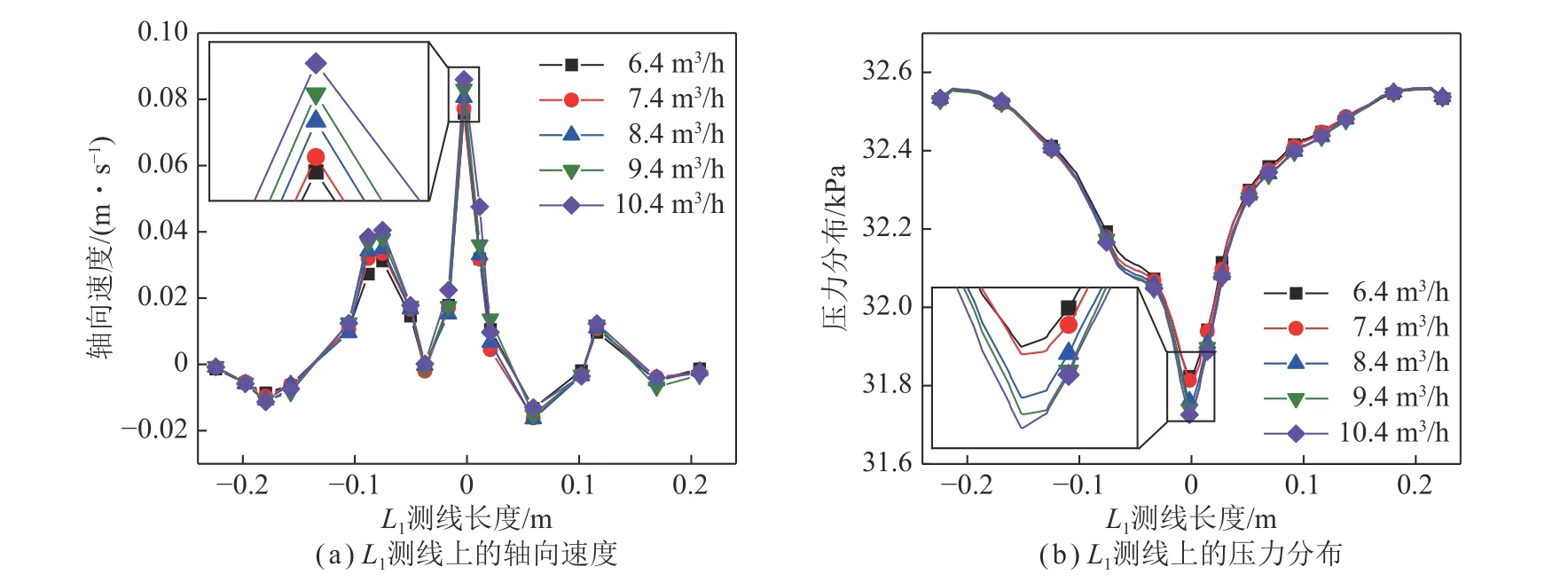
图23 注气量对L1 测线上速度及压力的影响Fig.23 Influence of gas injection on speed and pressure on L1 measuring line

图24 风管没入比对L1 测线上速度及压力的影响Fig.24 Influence of air duct submergence ratio on speed and pressure on L1 measuring line

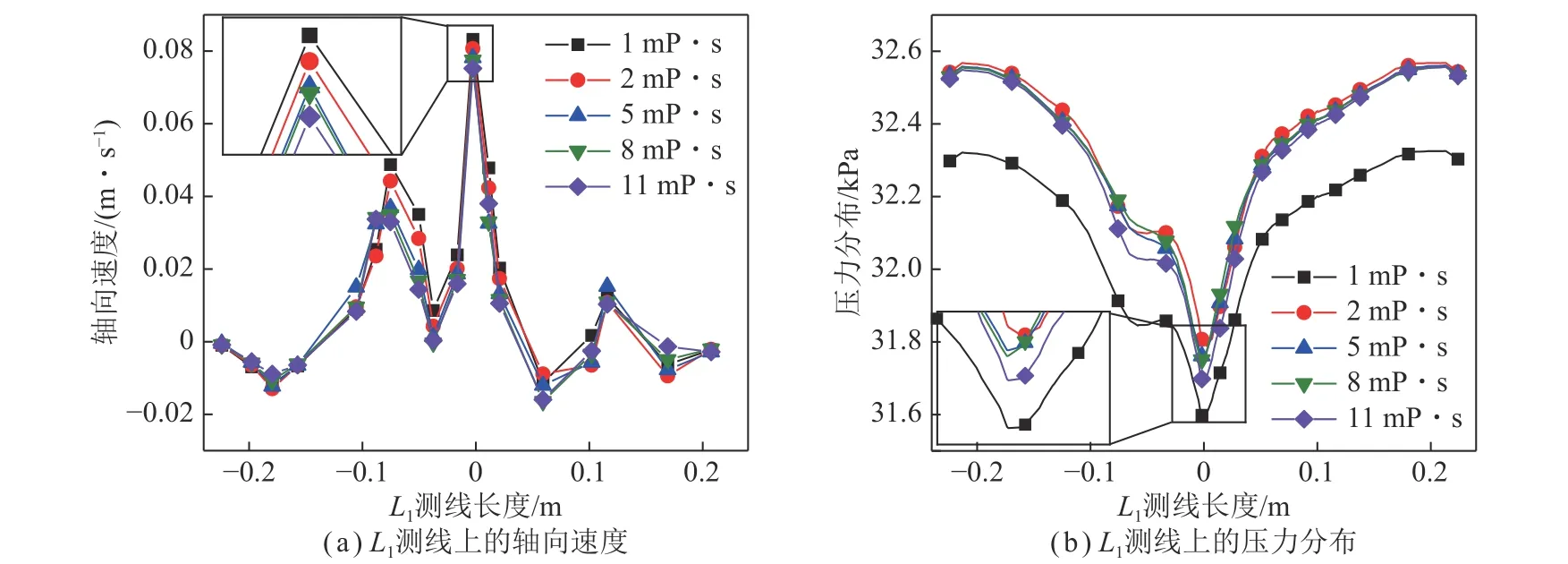
图25 泥浆黏度对L1 测线上速度及压力的影响Fig.25 Influence of mud viscosity on speed and pressure on L1 measuring line

(1)钻头转速对井底流体的速度场及压力场影响最为显著，井底流体的轴向速度随钻头转速呈先增大后降低趋势，且在35 r/min 时，井底流体的上返速度最大，井底压力则与钻头转速呈负相关关系，钻头转速由20 增至40 r/min 时，中心吸渣口、扫掠吸渣口与环空泥浆柱之间的压力差分别增大1.8 倍和4.3 倍，吸渣口吸附力显著增强。

(2)注气量、风管没入比与井底流体的轴向速度呈正相关关系，与井底压力呈负相关关系。当注气量由6.4 增至10.7 m3/h 时，中心吸渣口处流体轴向速度增长13.5%，井底与环空压差增大13.9%；当风管没入比由0.70 增至0.88 时，中心吸渣口处流体轴向速度增长30.4%，井底与环空压差增大13.6%，因此，增大风管注气量和埋入深度可显著增长井底流体的轴向速度和吸渣口吸附力。

(3)泥浆黏度与井底流体的轴向速度呈负相关关系，低黏流体易获取高返速，泥浆黏度由1 增至11 mPa·s 时，中心吸渣口和扫掠吸渣口处泥浆的轴向速度分别降低9.6%和32.3%；泥浆密度相同时，黏度对井底压力影响较小，但采用低密度泥浆时，井底和环空泥浆柱的压力骤然降低。

5 结 论

(1)排渣管内气-液-固混合流体的运移以轴向流动为主，途经注气端时，流速发生跳跃式剧增；井底流体的运移主要以水平流动为主，流体的垂直上返仅存在于吸渣口附近；井底水平流动以切向流动为主，径向流动仅在吸渣口两侧较为明显，且远离吸渣口处，径流速度较小易产生岩屑沉积。

(2)提出了优化刀盘吸渣口评判指标：清渣率η、泥浆输送比λ和气力输送比 ξ。依次改变刀盘吸渣口的数量、间距、面积比和总面积，通过数值模拟优化得到吸渣口的数量为2，长径比为0.4，面积比为1，总面积占比为1.94%时，吸渣口的布置方式最佳，其清渣率较现行吸渣口布置方式提高66%，且优化结果得到试验验证。

(3)钻头转速对井底流场的影响最为显著，增大钻头转速可显著降低井底压力，提高与环空泥浆柱间的压差，增强吸渣口的吸附作用；注气量、风管没入比与井底和排渣管内流体的轴向速度均呈正相关关系，低黏、低密度的泥浆易获取高返速，但携岩能力较差。

(4)基于钻井法气-液-固耦合流场分布规律，优化改变刀盘吸渣口布置及相应钻进参数，是提高侏罗系基岩钻井法凿井排渣和钻进效率重要的技术途径之一。但由于在钻进过程中存在岩性、刀具、泥浆等诸多综合影响因素，开展现场工业性试验研究将是今后不可或缺的重要环节。