地铁双线隧道下穿既有车站冻结加固冻胀控制措施

2024-04-25陈湘生李方政陈汉青

煤炭学报 2024年1期

陈湘生，丁航，李方政，陈曦，高伟，王恒，王磊，陈汉青

(1.煤炭科学研究总院, 北京 100013；2.深圳大学土木与交通工程学院, 广东深圳 518060；3.深圳大学未来地下城市研究院, 广东深圳 518060)

21 世纪是地下空间开发利用的世纪[1-3]。在城市土地与空间资源高度集约化利用的背景下，地下空间的开发利用已成为缓解地上建设空间压力的重要手段之一，而地下空间工程的安全高效建设至关重要。城市浅层土质多松软富水、稳定性较差，而国内外工程实践表明，冻结法仍是当前解决地下工程建设面临“水、软、变形难以预测”三大难题的一种灵活可靠绿色技术[4-6]。冻结法是通过人工制冷的方式使地层中的水结冰，在地层中形成一定厚度的冻结壁，提高土体强度且抵抗水土压力[7]，在冻结壁的保护下进行地下工程结构的掘砌施工；冻结法已在地铁车站出入口、地下换乘通道、地铁联络通道等城市地下工程中得到广泛的应用[8]。但在冻结施工过程中，地层水冰相变产生体积膨胀使地层冻胀变形[9-12]，若控制不当易出现地表建筑不均匀隆起、管线断裂等现象，甚至造成工程事故。

国内外学者针对市政冻结施工过程中冻胀效应展开研究，李方政[13]以上海体育场穿越工程为背景，采用随机介质理论，得出多管冻结冻胀叠加理论计算公式；季昌等[14]基于现场实测数据，结合数值计算分析，得出冻土体的实际冻胀率，并采取泄压控制冻胀；陶东军等[15]以苏州地铁某联络通道冻结工程为例，得出距离联络通道中轴线约25 m 范围内的地表变形受到冻结法施工的影响较大的结论；杨平[16]对软弱地层联络通道温度场及位移场进行了全程实测研究，基于实测数据得出地表冻胀融沉槽为联络通道中线两侧符合拟正态分布规律，其影响范围约为隧道底部埋深的1.2 倍。

以上工程中关于冻胀效应的研究成果多集中于联络通道，针对城市长距离大断面地下空间冻结工程的工况鲜有研究。类似地铁车站、隧道穿越等城市长距离大断面地下空间冻结工程的冻土体量约万方，是常规联络通道冻土体量的30 倍，冻胀效应显著；因此对城市长距离大断面地下空间冻结工程冻胀效应及控制措施的研究具有一定的必要性。为此，依托上海地铁18 号线国权路双线隧道下穿既有车站冻结工程，基于热力耦合方程，结合室内试验所得土体物理参数，对该工程进行数值分析，研究隧道冻结温度场及车站底板位移场演化规律，及不同冻胀控制措施对车站底板位移场的影响规律。经工程验证数值模拟方法可行、冻胀控制措施应用效果良好。以期为类似长距离大断面地下空间冻结工程设计施工提供参考。

1 工程概况

根据地质勘察资料，上海地铁18 号线国权路站隧道冻结工程下穿10 号线车站，隧道顶部埋深18.79 m，距离10 号线车站底板仅2.21 m，且车站下方存有4 道地连墙和钻孔灌注桩；隧道断面为圆形，管片外径6.6 m，壁厚0.35 m，拟冻结长度为36 m。冻结地层主要位于灰色黏土、灰色粉质黏土中，上述土层为典型的上海地区软土层；地层中的灰色淤泥质土具有高含水量、高压缩性、低强度等特点，易出现突发涌水流砂事故；隧道上方存有较多管线，若冻胀引起车站底板较大位移变形时，将导致车站底板开裂或管线破坏。

该隧道水平冻结加固设计采用“内圈孔+外圈孔+加强孔”理念，采用ϕ108 mm×10 mm 的低碳无缝钢管作冻结管、测温管及泄压管，上、下行线共布置126 个冻结孔、18 个测温孔，计划双线隧道同时冻结时积极冻结期45 d，上、下行线冻结壁厚度设计值为2 m、冻结壁的平均温度不低于-10 ℃。国权路隧道冻结如图1 所示。

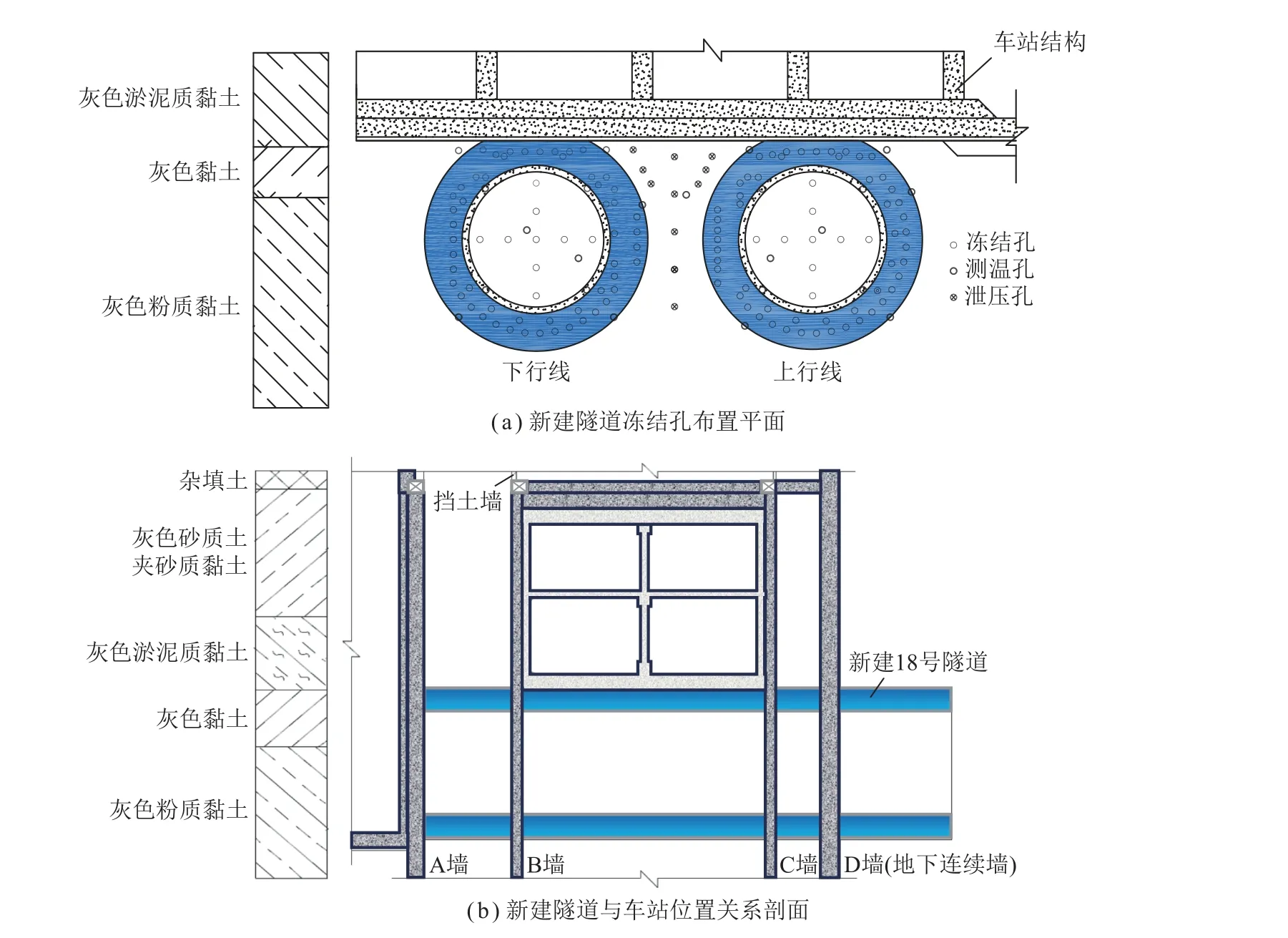
图1 国权路隧道冻结示意Fig.1 Freezing schematic diagram of Guoquan Road Tunnel

2 冻结热力耦合机制

2.1 基本假定

冻结施工期间温度场是与空间、时间相关的瞬态温度场，冻结过程中包含相变、冻结锋面迁移、对流换热等物理现象，影响因素众多。因此假设：① 不考虑土体中水渗流对冻结壁发育的影响；② 冻结管壁温度近似为盐水温度；③ 水冰相变仅发生在[Tm,0]内，其中，Tm为结冰点温度。

2.2 控制方程

2.2.1 温度场方程

根据孔隙介质的热传导原理，其温度场控制方程[5]为

式中，Ceq为等效体积热容，kJ/(m3·℃)；T为土体温度，℃；t为时间，s；Keq为等效导热系数，W/(m·℃)；q为相变潜热，kJ/m3；Qm为热源汇。

该方程的初始条件与边界条件为

式中，T0为土体的初始温度，℃；r为距离冻结管外壁的长度，m；Ty为盐水温度，℃。

空气与冻结壁交界面处的对流换热边界条件为

式中，Ta为大气温度，℃；n1为地表的法线方向矢量；hf为大气与土体的对流换热系数，kJ/(m2·s·℃)。

2.2.2 本构方程

冻结法施工时，土体中发生水冰相变，土体弹性模量随温度降低而逐渐增大，土体中应力随温度变化。因此除考虑力场作用下土体应力和应变外，还需要考虑温度场对土体力场的影响。基于弹性力学，建立热应力方程，其应力-应变关系[5]为

式中，x、y、z为x方向、y方向、z方向；E(T)为弹性模量随温度变化的关系式，MPa；α(T)为热膨胀系数随温度变化的关系式；Δt为温度变化。

结合冻结温度场控制方程与土体热力本构方程，得出人工冻结条件下热力耦合控制方程。由该方程可知，冻胀量与土体膨胀系数及温差有关，减小冻胀量需要控制土体温度梯度及减小土体膨胀系数；因此在城市长距离大断面地下空间冻结工程中可以通过改变盐水温度梯度、错峰冻结及改良土体冻胀特性[17]等措施以实现冻胀控制。

2.3 计算参数取值

采用ISOMET 热导仪对国权路灰色粉质黏土导热系数及比热进行测定，所得数据如图2 所示。由图2 可以看出，随着冻结温度不断降低，灰色粉质黏土的导热系数不断增高，2 者之间近似呈线性变化；灰色粉质黏土的比热容随冻结温度降低而降低，2 者之间亦近似呈线性变化。采用XT5201FST 冻土冻结温度测定仪测定了灰色粉质黏土的结冰温度为-0.51 ℃。

图2 热物理参数与温度之间关系Fig.2 Relationship curve between thermophysical parameters and temperature

冻土弹性模量取瞬时抗压强度(σs)的一半与其所对应的应变值(ε/2)的比值。试验得到的土样弹性模量随温度的变化规律如图3 所示。由图3 可以看出，在本试验区间内，弹性模量与温度之间近似呈指数变化，当冻结温度由-10℃降至-15 ℃，冻土弹性模量增加61.1 MPa。

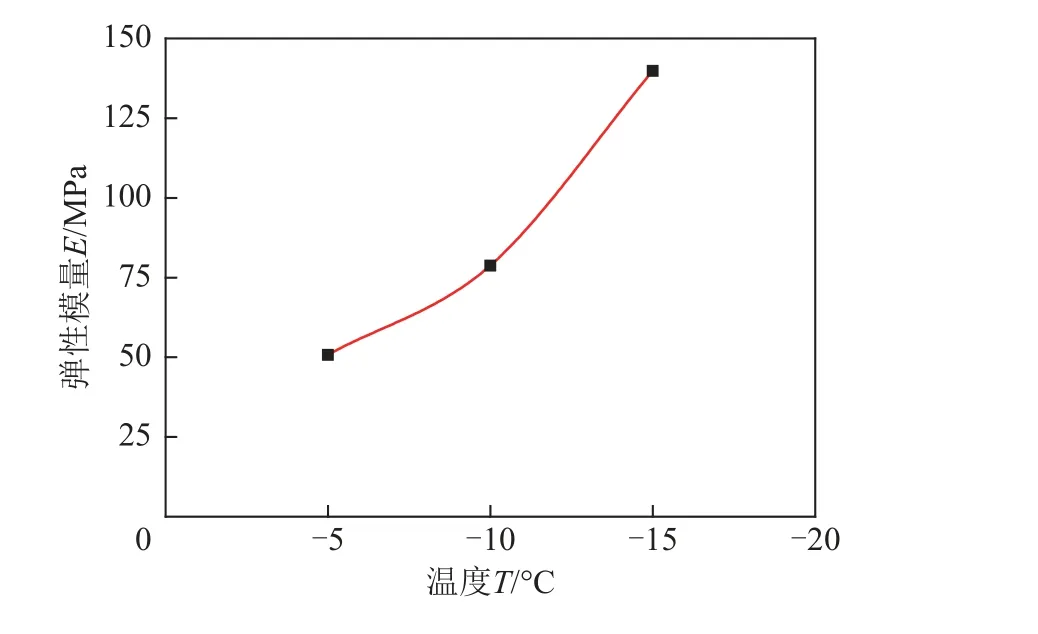
图3 弹性模量与温度之间关系Fig.3 Relationship curve between elastic modulus and temperature

进行无水源补给封闭条件下的单向冻胀试验[18-19]，采用XT5405B 型冻胀仪测定-5、-10、-15 ℃时灰色粉质黏土冻胀率；试验得到的不同冷端温度下土样冻胀率随时间变化的规律曲线如图4 所示。由图4 可以看出，不同冷端温度下，土体冻胀率随时间变化规律基本一致，可大致分为3 个阶段：① 快速增长阶段(0～10 h)。此阶段当冷端温度越低，冻胀率曲线曲率越大，增长速率越快。② 缓慢增长阶段(11～25 h)。此阶段当冷端温度越低，土体冻胀率越快地进入稳定阶段。③ 稳定阶段(26～80 h)。此阶段土体冻胀率增速都趋于平缓。

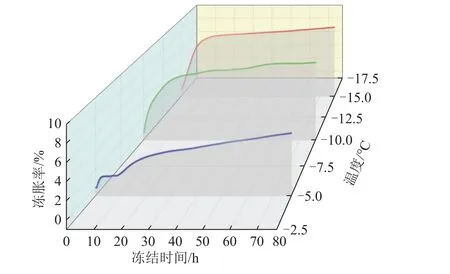
图4 不同温度下土体冻胀率与时间的关系曲线Fig.4 Relationship curves between frost heave rate and time at different temperatures

3 工程案例数值分析

3.1 数值计算模型

基于热力耦合方程，结合室内试验获得灰色粉质黏土热物理参数；通过编写APDL 程序，实现土体热物理力学参数随温度变化进行调整，从而建立了计算参数随温度场变化的热力耦合数值模型；研究地铁双线隧道下穿既有车站时隧道冻结温度场、车站底板冻胀位移场演化规律。

考虑到冻结施工对周边环境的影响及边界效应对计算结果的影响，计算模型在X轴、Y轴、Z轴方向上尺寸分别取85、50、40 m；建立如图5 所示的有限元模型。为简化计算，视隧道全部处于灰色粉质黏土层中；当土体温度低于-0.51 ℃时，认为此处土体已由未冻土转化成冻土。模型边界条件为：假定隧道周围土体初始地温为20 ℃；冻结管壁温度为实际盐水降温曲线；模型底面设置为垂直约束，4 个侧面设置法向约束，模型顶面设置为自由边界条件。

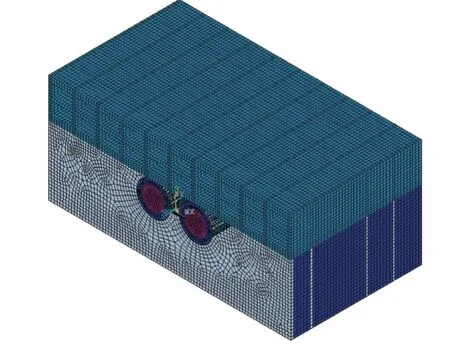
图5 有限元模型Fig.5 Finite element model

为研究隧道下穿车站冻胀位移场演化规律，参照现场监测点的位置在车站底板布设D1、D2、D3 三个位移监测点，用于监测冻胀引起的竖向位移演化规律，监测点位置如图6 所示。考虑到调整盐水温度会延长积极冻结期[20-23]；因此将双线隧道同时冻结、错峰冻结、调整盐水温度这3 种冻结模式的冻结时间统一为90 d，以冻结90 d 时冻胀引起的监测点竖向位移量为指标，研究错峰冻结、调整盐水温度等措施的冻胀控制效果。数值计算采用热膨胀系数模拟土体冻胀过程。基于不同温度下的土体冻胀率与时间的关系曲线，结合模型试验数据[24]，对热膨胀系数取值进行迭代优化，反演出更符合本工况下的热膨胀系数。

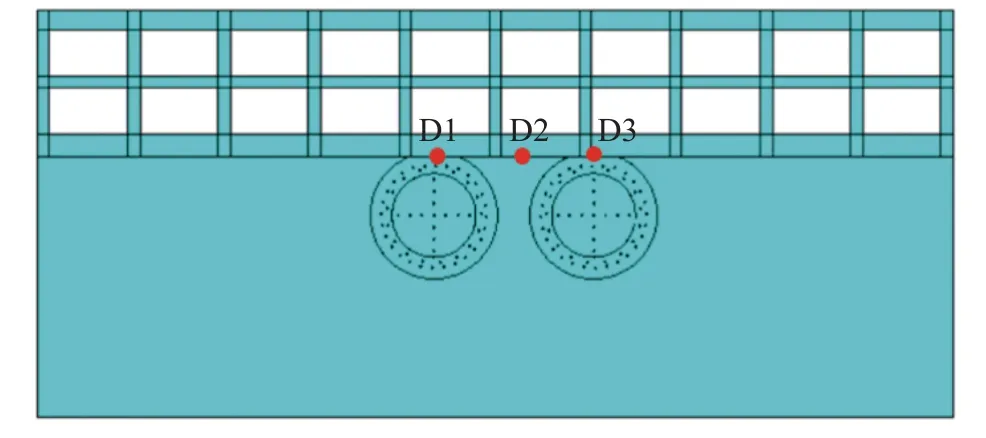
图6 监测点布置Fig.6 Layout of monitoring points

3.2 计算结果分析

3.2.1 冻结温度场演化规律

冻结45 d 时的隧道冻结温度场分布规律如图7所示。当冻结进行到45 d 时，冻结壁厚度达到2.2 m、平均温度为-19 ℃，均超过设计值，待开挖冻土量较大。基于冻结温度场演化规律分析可知，该设计方案偏保守；因此在实际冻结施工中，可通过调低盐水温度、错峰冻结等措施来降低冻土体量。

图7 隧道温度场剖面Fig.7 Tunnel temperature field profile

3.2.2 冻胀位移场演化规律

冻结45 d 时的冻胀位移场分布规律如图8 所示。由图8 可知，隧道周边土体及车站都因冻胀效应发生竖向位移；车站底板最大竖向位移在冻结壁与车站底板交界面处，位移为28.425 mm。靠近冻结壁区域的土体、车站底板竖向位移较为明显，远离冻结壁区域土体、车站底板竖向位移逐渐减小，表明冻胀效应对周边环境的影响程度随着远离冻结壁逐渐减弱。

图8 冻胀位移场云图Fig.8 Cloud image of frost heave displacement field

监测点D1、D2、D3 的时间位移曲线如图9 所示。冻结期间，冻胀引起车站底板位移的演化规律大致分为3 个阶段。以监测点D1 为例：① 位移快速增长阶段(0～20 d)。冻结20 d 时，位移达到17.48 mm；位移平均增速为0.87 mm/d，表明冻胀现象显著。② 位移缓慢增长阶段(21～45 d)。冻结45 d 时，位移达到27.91 mm；位移平均增速为0.42 mm/d，冻胀位移平均增速减缓，表明冻胀现象减弱。③ 位移趋于稳定阶段(46～90 d)。冻结90 d 时，位移达到34.43 mm；位移平均增速为0.14 mm/d，表明冻胀现象趋于稳定。分析可知，冻胀引起的位移场与冻结壁存在密切联系；冻结壁交圈前，冻胀位移变化量明显，冻结壁交圈后，冻胀位移变化量随冻结壁厚度增加线性上升；在冻结后期，冻胀位移变化量趋于平缓。数值计算未考虑取土泄压等工况对冻胀的抑制作用，用该方法模拟预测冻胀变形时需对计算结果相应折减以符合实际工况。

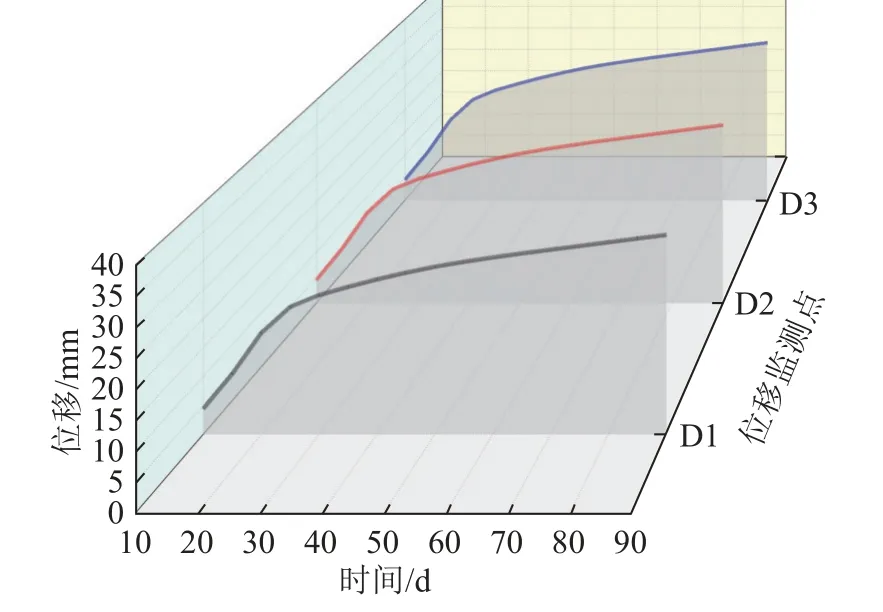
图9 车站底板位移变化曲线Fig.9 Displacement curves of station floor

3.3 冻胀控制措施分析

3.3.1 错峰冻结

下行线先行冻结45 d 后，上行线再冻结45 d。冻结期间，监测点D1、D2、D3 的时间位移曲线如图10所示。由图10 可知，冻结初期，由于上行线未形成冻结壁，下行线冻结壁周围土层冻胀现象更为明显；冻结45 d 时，测点D1、D3 位移分别为12.78、11.08 mm，测点D1 位移较测点D3 位移高出13.4%；冻结45 d后，上行线也进入积极冻结期，测点D1 与测点D3间位移差距不断减小；冻结90 d 时，两者间差距仅为0.07 mm。冻结45 d 时，测点D1 位移为12.78 mm，为双线隧道同时冻结时位移量的45.8%；冻结90 d 时，测点D1 位移为31.78 mm，较双线隧道同时冻结时减小了2.65 mm，位移量减小7.7%。

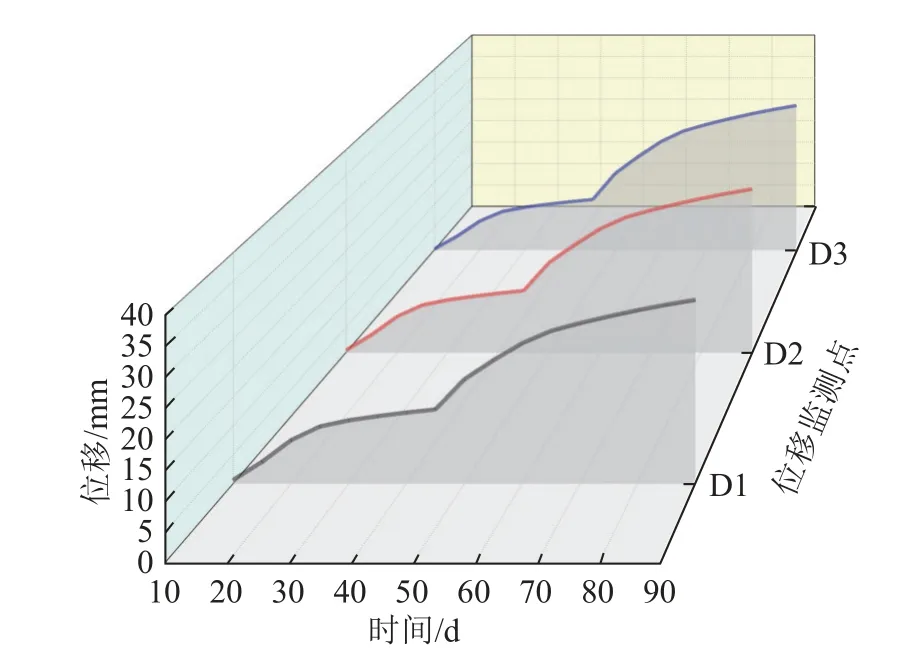
图10 错峰冻结下车站底板位移变化曲线Fig.10 Displacement curves of station floor under the staggered peak freezing

采用错峰冻结模式延长了车站底板位移达到峰值的时间点，避免了同一时间段内冻胀的叠加效应；采用错峰冻结能在一定程度上减小冻胀效应，但冻胀效应的显著程度主要受冻土体量的影响。当冻结工期较为宽松时，可采取错峰冻结模式避免冻胀的叠加效应，以减轻同一时间段冻胀对地表构筑物的影响。

3.3.2 调整盐水温度

调整盐水温度是将盐水温度由-28 ℃调整至-20 ℃。冻结期间，监测点D1、D2、D3 的时间位移曲线如图11所示。由图11 可知，各监测点冻胀量随时间变化的规律与采用-28 ℃盐水冻结时的规律基本一致；冻结90 d 时，测点D1 位移为22.63 mm，位移较同时冻结模式下时降低了34.2%。冻结前30 d 时，各测点位移与时间呈线性关系，平均增速为0.54 mm/d；冻结31～50 d 时，冻胀现象减弱，平均增速为0.15 mm/d；冻结51～90 d 时，冻胀位移呈缓慢增长趋势，平均增速为0.08 mm/d，即冻结后期冻胀现象趋于稳定。

图11 调整盐水温度下车站底板位移变化曲线Fig.11 Displacement curves of station floor under the adjustment of brine temperature

盐水温度为-20 ℃时，土体的降温速度较慢，冻胀引起车站底板位移明显降低；通过调整盐水温度，在保证冻结壁厚度及完整性的基础上，通过控制冻土发展速率减小冻土体量，以减小冻胀效应。

4 工程应用效果实测分析

基于数值分析得出的不同冻胀控制措施下车站底板位移演化规律，提出在工程实践中采取调整盐水温度、错峰冻结等措施协同控制冻胀对车站结构的影响。在10 号线国权路车站轨行区布设车站结构竖向变形监测点D1、D2、D3，测点的布设位置如图12 所示。

图12 车站结构变形监测布点Fig.12 Layout of monitoring points for structural deformation of stations

实际施工中，为保证冻结质量，对积极冻结时间进行了延长；选取测点从2019-01-04—2020-05-28的竖向位移数据，测点的竖向位移量随时间的变化曲线如图13 所示，图中Tn(n=1，2，…，10)为不同施工工序的时间节点。

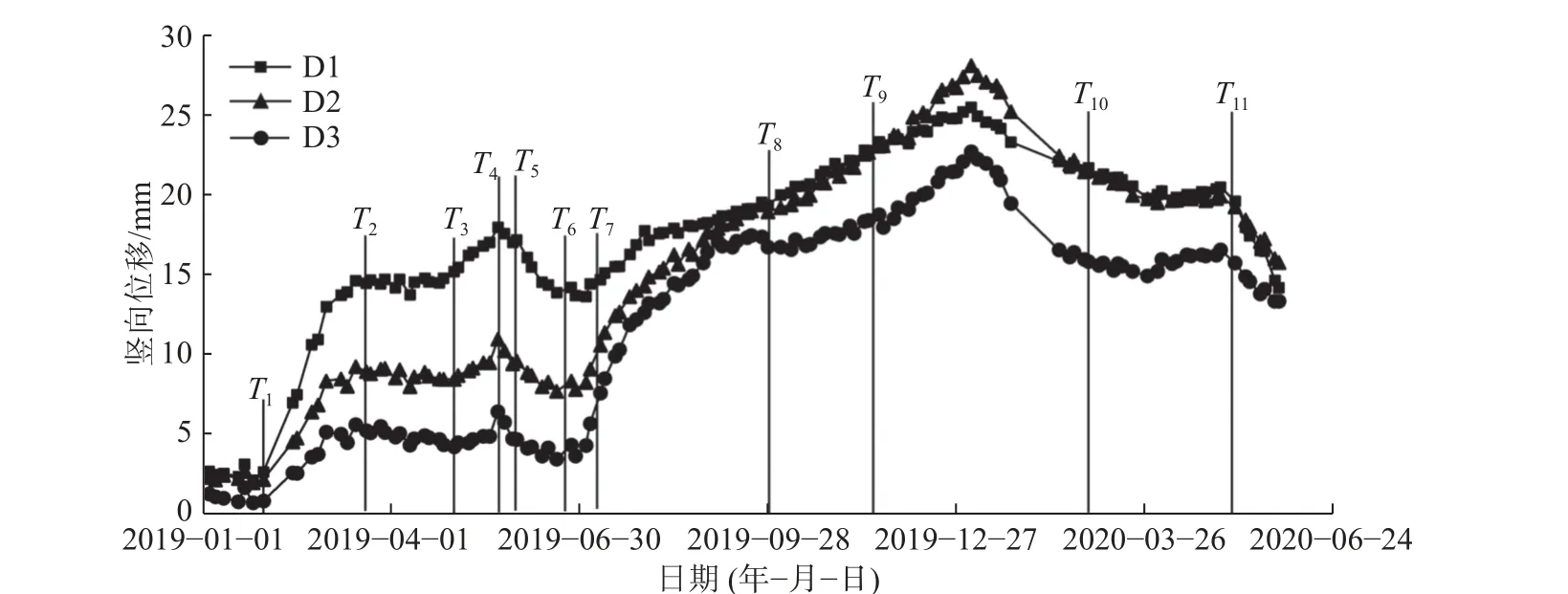
图13 监测点竖向变形实测曲线Fig.13 Measured vertical displacement curves of monitoring points

(1)错峰冻结。

选取D1、D2、D3 进行变形速率分析，见表1。2019-05-15(T4时刻)上行线进行开机试冻结，冻结7 d后停止冻结；此时下行线BC 段(B 墙—C 墙)尚未开挖。以测点D1 为例：5 月15 日测点的竖向变形为16.78 mm，5 月22 日测点的竖向变形为17.95 mm，冻胀引起的车站底板位移平均变化速率为0.18 mm/d。7 月1 日(T7时刻)上行线再次开始开机冻结，此时测点的竖向变形为13.69 mm，7 月7 日测点的竖向变形为14.42 mm，冻胀引起的车站底板位移平均变化速率为0.10 mm/d。分析原因，上行线第1 次全线冻结时，下行线仍处于积极冻结阶段，存在冻胀叠加作用，导致车站结构的竖向变形增长速率较快；上行线第2 次全线冻结时，此时下行线(B 墙—C 墙)已开挖完成，下行线冻结对车站影响较小。监测点实测位移演化规律与数值模拟规律基本一致，错峰冻结时双线隧道上方车站底板同时抬升，其中先行冻结区域冻胀引起的位移更为明显；说明数值模型能较好地模拟冻胀过程。

表1 错峰冻结下监测点的竖向变形量Table 1 Vertical displacement of monitoring points under the staggered peak freezing

(2)调整盐水温度。

选取D1、D2、D3 进行变形速率分析，见表2。上、下行线隧道在积极冻结期间盐水温度为-25 ℃。上、下行线隧道开挖完成后，开始填充泡沫混凝土。全部施工工序完成，2020-02-28 将盐水温度调整为-10 ℃，通过维护冻结(T10—T11阶段)在保证冻结壁完整的前提下控制冻土扩展速率。以测点D1 为例：① 盐水温度为-25 ℃时，2019-01-30 测点的竖向变形量为2.66 mm，2019-03-15 测点的竖向变形量为14.62 mm，冻胀引起的车站底板位移平均变化速率为0.27 mm/d。② 盐水温度为-10 ℃时，2020-02-28 测点的竖向变形为21.65 mm，2020-05-01 测点的竖向变形为20.46 mm，冻胀引起的车站底板位移平均变化速率为-0.02 mm/d，即车站结构竖向位移基本保持不变。

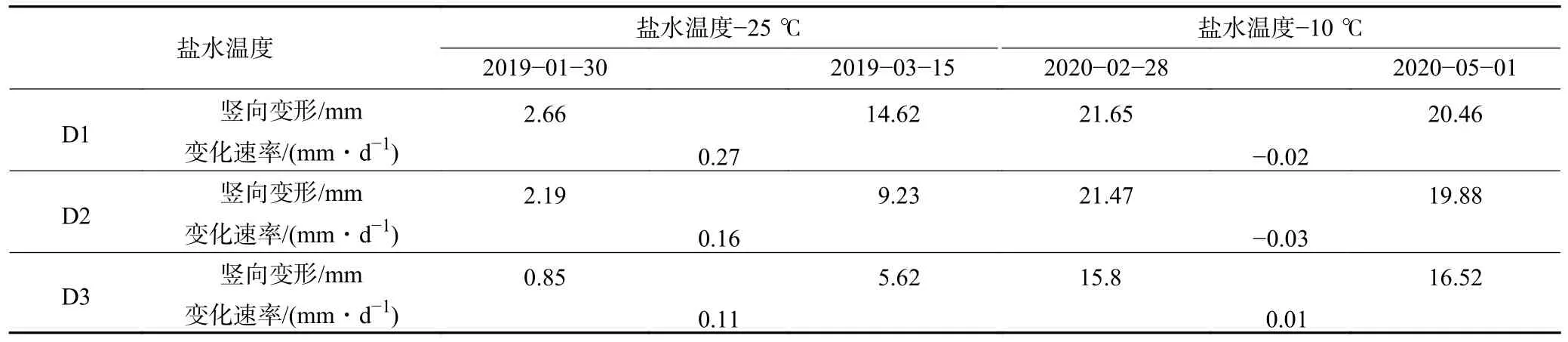
表2 不同温度盐水冻结时监测点的竖向变形量Table 2 Vertical deformation of monitoring points during freezing at different brine temperatures

分析原因，调整盐水温度与间歇冻结控制冻胀的机理是一致的，较高的冻结温度使土体内的温度梯度较小，导致冻结锋面的水分迁移量小，从而抑制了冻胀的产生；同时通过控制冻土发展速率减小冻土体量，以减小冻胀效应。监测点实测位移演化规律与数值模拟规律基本一致，均表现为车站底板位移影响受盐水温度影响较为显著，盐水温度越低，冻胀引起的车站底板位移越大，说明数值模型能较好地模拟冻胀过程。