重离子相对生物效应的双尺度模拟方法比较研究
2024-04-24胡子仪陈宜正胡安康李君利
胡子仪,邱 睿,*,陈宜正,胡安康,武 祯,张 辉,李君利
(1.清华大学 工程物理系,北京 100084;2.清华大学 粒子与辐射成像教育部重点实验室,北京 100084;3.同方威视技术股份有限公司,北京 100084;4.斯坦福大学 放射肿瘤系,美国 斯坦福 94305)
放射治疗是指利用光子、质子或重离子等射线照射肿瘤细胞,通过射线的生物物理作用达到杀伤肿瘤细胞的目的,是治疗癌症的重要手段。全世界约有2/3癌症患者在治疗中使用放射疗法。相比于传统光子放疗,重离子放疗具有更多优点[1]。物理方面,重离子的能量主要沉积在径迹末端,呈布拉格峰形式,从而可在靶区沉积较多物理剂量的同时减少周边正常组织的受照剂量;生物方面,由于重离子是高传能线密度(linear energy transfer, LET)射线,因而在相同物理剂量下重离子相比光子具有更强的肿瘤杀伤效应。国内外开展重离子放疗的时间较短,需借鉴已有的大量光子放疗的经验,因此引入相对生物效应(relative biological effectiveness, RBE)的概念。定义RBE为产生相同辐射生物效应时,光子与重离子物理剂量的比值[2]为RBE=DX/DC。重离子RBE受到射线种类和能量、剂量水平、细胞种类以及生物终点等因素的影响[3-4]。重离子临床放疗中,不仅需计算人体内的物理剂量分布,还需确定RBE的分布,最终根据RBE加权物理剂量设计治疗计划。因此,准确评估RBE对于重离子精准放疗具有重要意义。
国内外已有较多针对重离子RBE的研究工作。早期的线性平方(LQ)模型基于双重辐射作用理论,建立了光子照射下的离体细胞存活分数与辐射物理剂量的线性平方的关系[5-6]。通过经验地拟合LQ模型的一次项系数α和二次项系数β与射线品质的关系,日本国立放射医学研究所(NIRS)建立了针对重离子的LQ模型。但LQ模型基于大量实验值的经验拟合,难以解释辐射生物效应的机理。NIRS进一步通过分析辐射生物效应机理,建立和求解微观生物动力学方程,研发了微剂量动力学(MKM)模型[7-9],能较好体现细胞存活生物效应与重离子微观辐射场之间的关系。LQ模型和MKM模型均已应用于国内外重离子临床放疗的RBE计算中。
现有的重离子RBE研究分析通常只针对单一的宏观或者微观尺度。本研究基于双尺度剂量学的方法,同时在宏观和微观两个尺度蒙特卡罗模拟计算重离子辐射场中的物理量分布。进而针对两个尺度分别采用不同的模型,即宏观尺度采用LQ模型,微观尺度采用MKM模型,对比分析RBE分布,为重离子临床放疗提供参考。此外,已有研究中微剂量模拟通常放置不同厚度的水或组织等效材料在放射源和微剂量探测器之间来等效人体中的不同深度[10],本研究用二次源项的方法将宏观和微观模拟联系起来,使微观模拟的源项更符合实际照射情况。
1 材料与方法
1.1 宏观重离子RBE的计算
宏观尺度重离子RBE的计算采用的是LQ模型(式(1))[11],SF为细胞存活分数,D为光子或质子的剂量,α和β为模型参数。根据RBE定义式,可给出细胞存活分数为SF时的12C离子RBE的表达式(式(2))。
SF(D)=e-αD-βD2
(1)
(2)
式(2)中αx和βx表示200 kVp X射线LQ模型参数,根据离体HSG细胞存活实验结果的拟合得到[7],αx=0.19 Gy-1,βx=0.05 Gy-2;重离子LQ模型进一步经验地建立了αc和βc参数值与重离子LET值的变化关系。Furusawa等[12]使用不同LET值的单能重离子,针对人类唾液腺(HSG)细胞开展了体外照射实验。Kase等[13]基于实验数据拟合了HSG细胞的12C离子LQ模型参数和LET的关系曲线。
蒙特卡罗模拟中每个体素i的LQ模型参数α和β按下式计算:
(3)
(4)
式中:a(LETi,j)和β(LETi,j)为第j个粒子入射第i个体素的LQ模型参数,根据Kase等拟合的α-LETd曲线和β-LETd曲线插值得到;εi,j为第j个粒子入射第i个体素沉积的能量。
1.2 微观12C离子RBE计算方法
微观尺度12C离子RBE的计算使用日本NIRS建立的MKM模型[7,14]。MKM模型基于双重辐射作用理论,建立亚细胞核体积区域内的细胞致死事件数与其内沉积线能的关系,并得到模型表达式(式(1),其中α有式(5))。
(5)
式中,y*为饱和校正的剂量平均线能,体现了重离子辐射品质对细胞存活效应的影响,可根据domain中的线能和线能谱,即y和f(y)来计算,计算式为:
(6)
式中,y0为饱和参数,它只与domain半径rd和细胞核半径Rn以及细胞的β参数有关:
(7)
MKM模型中假设α0、rd、Rn和β参数只与所研究的细胞种类有关,和射线种类、LET值等因素无关。对于HSG细胞,β=0.05 Gy-2。戴天缘等[15]根据细胞实验数据和微剂量蒙特卡罗模拟结果优化了HSG细胞的模型参数,其中α0=0.12 Gy-1,rd=0.39 μm,Rn=3.7 μm,y0=126 keV/μm。根据MKM模型表达式(式(1))和RBE定义(式(2))可计算微观尺度的12C离子RBE。
1.3 重离子RBE蒙特卡罗模拟
本研究基于双尺度蒙特卡罗模拟方法计算重离子RBE。使用蒙特卡罗模拟软件Geant4,选取QGSP_BIC_EMY物理列表模拟重离子在水体中的物理相互作用过程。初始粒子数设为106以确保模拟精度,宏观模拟的步长设置为0.1 mm,微观模拟的步长设置为3 nm。宏观模拟使用水体素模型,尺寸为200 mm×200 mm×200 mm,体素尺寸为1 mm×1 mm×1 mm;290 MeV/u的12C粒子穿过脊型过滤器后入射到水模型,如图1a所示。统计每个体素中沉积的物理剂量、剂量加权平均的LET值(LETd)、αi和βi。从而可根据LQ模型计算宏观12C粒子RBE在人体中随深度的分布。同时,宏观模拟中记录不同深度处粒子通过体素的信息,即体素中通过的粒子的种类、能量、位置和方向,作为微观模拟的二次源项入射到组织等校正比计数器(TEPC)中进行微剂量模拟,如图1b所示,进而得到不同深度处像空间粒子的线能谱,基于MKM模型计算微观RBE。

图1 宏观(a)和微观(b)蒙特卡罗模拟示意图
2 结果
宏观模拟统计的12C离子束物理剂量和LETd随深度的分布如图2所示。其中剂量和LETd的统计不确定度均小于1%。布拉格峰展宽的深度为99~157 mm,在布拉格峰入口12C的LET从40.7 keV/μm逐渐增加,在布拉格峰尾部,即156.5 mm处达到最大值232.9 keV/μm。在布拉格峰展宽入口,吸收剂量最高为坪区的1.45倍,在布拉格峰后158~200 mm范围,由于核碎片的存在,吸收剂量有拖尾。
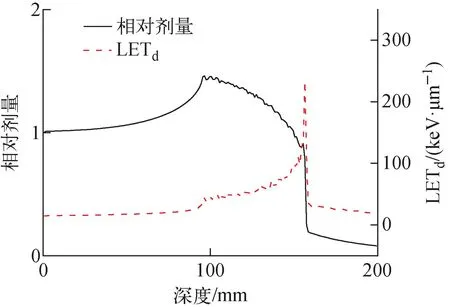
图2 宏观剂量和LETd在水体中随深度的分布
微剂量模拟得到不同深度像空间粒子的微剂量谱,如图3所示。图3a为坪区(0~90 mm)模拟得到的微剂量谱,在坪区深度,随着深度的增加,微剂量谱的峰位向高线能区移动,且谱宽度逐渐增加,峰值从1.2逐渐降至0.6,这是因为随着深度的增加,初级12C粒子的能量逐渐降低,单次能量沉积事件中损失的能量增加;图3b(100~160 mm)为峰区模拟得到的微剂量谱,随着深度的增加,峰位仍向高线能区移动,宽度增加,峰值下降。但在峰区尾部,即深度160 mm处,由于尾部出现了较多的低线能的核碎片,微剂量谱的峰位向低线能区移动,且谱的形状出现不规则。
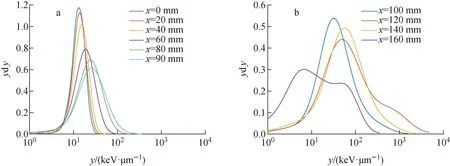
图3 不同深度处的微剂量谱
图4给出了存活分数SF=0.1时,宏观和微观两个尺度12C离子RBE随深度分布曲线。在两个尺度均可看到相似的RBE变化趋势。在坪区12C宏观RBE为1.40~1.67,微观RBE为1.22~1.45,宏观RBE较微观高约16%;在布拉格峰区,宏观RBE从1.86迅速上升,在布拉格峰末尾达到最大值3.18,微观RBE从1.63增加到2.47,宏观RBE较微观高约25%。
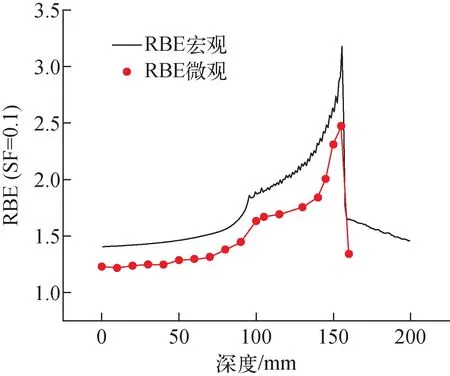
图4 SF=0.1时宏观和微观12C RBE随深度的分布
3 RBE讨论
在宏观和微观模型中都包含剂量D的一次系数α和二次系数β,图5给出了LQ模型和MKM模型计算的12C离子宏观和微观α和β参数随深度的分布。两个尺度的α参数变化趋势相同,宏观α普遍大于微观α,但β的变化趋势有明显的不同。由于MKM模型假设亚细胞区域内的致死和亚致死事件数只和该区域中沉积的比能有关,而忽略了射线种类和LET等因素的影响,因此MKM模型的β是常数(图5),不随射线LET变化而变化。但大量离体细胞实验结果显示[16],剂量二次项系数β是随射线LET值变化而变化的。根据宏观RBE计算方法得到的β在12C离子布拉格峰对应的高LET处有明显下降,但MKM模型的计算结果并没有体现这一变化趋势,因此MKM模型的常数β在RBE的计算中具有较大的局限性。特别是在高剂量水平下,由于β是模型的二次项系数,对于RBE的影响会更大。
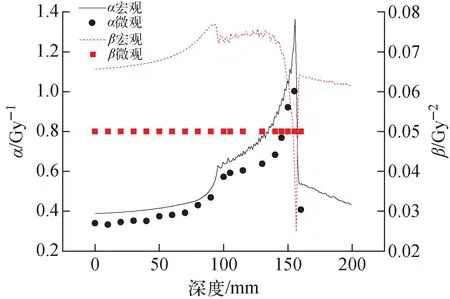
图5 宏观和微观12C α和β参数随深度的分布
在10%的存活分数下,宏观RBE普遍大于微观(图4),通过分析宏观和微观RBE的差别可解释这种差异:宏观RBE计算所采用的实验数据是单能12C离子照射离体细胞,并拟合得到α和β参数关于LET的函数关系[13],然而宏观RBE的模拟计算中,计算体素平均α和β时没有考虑实际照射的辐射场中包含很多除初级12C离子外其他次级粒子,这些次级粒子具有相同的LET时其LQ模型参数小于12C。计算中忽略了粒子类型的影响,因此会高估实际辐射场的RBE。
12C离子的RBE还受剂量水平的影响。图6给出了不同存活分数下两个尺度重离子RBE的对比。12C离子RBE随剂量水平的降低而增加,其离差列于表1。从表1可看到,宏观和微观模型差异对12C离子RBE的影响主要体现在峰区,在不同的存活分数下,峰区RBE的差别总大于坪区,原因主要是峰区剂量大于坪区剂量,且微观MKM模型中将β设置为常数,在高剂量水平下会引起更明显的差异。

表1 不同存活分数宏观和微观12C离子RBE的离差
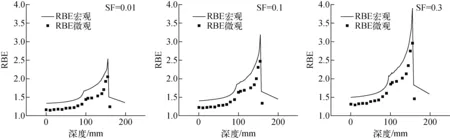
图6 不同存活分数的12C离子RBE
宏观LQ模型以及微观MKM模型的局限需改进。对于宏观LQ模型,实际治疗中辐射场是由初级粒子以及多种次级粒子组成的,需通过实验获得不同粒子的α-LET和β-LET曲线,再进一步进行RBE计算,然而LQ模型是现象模型,不能解释辐射生物效应的机理;对于微观MKM模型,Chen等[17]已在相关研究中对其进行改进,将MKM模型的辐射损伤和修复参数与射线品质联系起来,并考虑了DNA损伤产额、微观比能分布以及宏观物理剂量对生物RBE的影响,从而建立了改进的MKM模型,但尚未应用于临床。
4 结论
本研究首次开展了双尺度剂量学方法比较研究,对同一照射情况分别开展了宏观和微观RBE模拟,并对宏观和微观RBE结果进行了分析,相同照射条件下计算出的宏观和微观RBE的差别也对RBE模型的改进有参考价值。且本文建立的基于二次源项的微观RBE模拟方法,可直接获得实际照射情形下,如放疗中患者体内局部的复杂粒子信息以进行更精确的微剂量模拟。本研究模拟了展宽12C离子平行束照射水体素模型,与临床重离子放疗照射情形有一定差别;且细胞的生物参数均针对人类唾液腺HSG细胞,缺少不同的组织器官的实际细胞参数,需开展进一步研究。本文提出的双尺度模拟方法将为重离子RBE的研究提供一种新的思路。由于这两种尺度的RBE计算方法均已应用于临床,本研究的结果将为不同方法所得12C离子放疗中RBE加权剂量分布的分析对比提供参考。
