基于正交切削理论的PDC钻头切削齿动态破岩温度分布

李 波，何志波，梁春平，张古森，林 伟

（1. 西南石油大学机电工程学院，四川 成都 610500；2. 中国石油集团西部钻探工程有限公司玉门钻井分公司，甘肃 酒泉 735000；3. 中石化中原石油工程有限公司管具公司，河南 濮阳 457300）

0 引言

钻头是油气钻井必不可少的切削工具，其呈现出的力学特性与钻井效率、成孔质量有重要关系。随着井深的增加，PDC钻头遇到的地层变得越来越复杂，成孔所需的钻进过程给钻头带来了更大的挑战性，因此，从设计角度解决设计的钻头与地层的适应性难题，以及提高钻井效率成为众多学者的研究热点。PDC钻头切削井底岩石形成复杂的井眼轨迹，在这一过程中，切削齿与岩石的相互作用至关重要。然而，切削齿与岩石的接触与摩擦往往会导致切削齿的磨损，进而影响钻进效果。更为严重的是，摩擦产生的大量热量会显著提高PDC钻头切削齿的温度，进一步加剧切削齿的磨损[1]。PDC钻头切削齿的失效与工作温度密切相关，积聚的热量过多，温度过高，将加速切削齿的破损，降低钻头寿命[2-3]。鉴于此，深入预测分析切削齿的温度分布特性，掌握耦合温度-位移破岩过程本质，对钻头破损机理研究、提高钻头寿命有重要意义，可为PDC钻头结构优化设计奠定基础。

陈浩等[4]进行PDC单齿切削破岩室内试验，将花岗岩和砂岩加热至不同温度以模拟深部井底高温岩石，获得了不同温度岩样的切削力、破岩过程和切削温度场；李玮等[5]进行了不同钻压和转速、高温高压下不同岩样的正交实验，得到200°高温及高压条件对钻头的破岩规律及磨损规律的影响；马亚超等[6]基于磨料磨损理论、微积分基本理论和迭代算法，构建了变温变载影响PDC钻头切削齿体积磨损量和线磨损量之间的函数关系以及切削齿隐式线磨损模型，提出了PDC钻头动态磨损趋势预测方法；周波等[7]基于高温高压钻井模拟装置，测试分析了温度、压力对岩石等效可钻性级值的影响，指出高温高压地层钻井时，设计钻头应考虑温度、压力的影响，通过优化钻井参数，可有效提升钻头破岩效率；李勇等[8-9]和邓嵘等[10]建立了二维和三维PDC钻头切削齿非线性切削模型，通过改变二维平面模型中切削齿的切削参数，得到了切削温度场分布规律；祝效华等[11]利用实验获得了岩石在不同温度下的本构模型，通过模拟不同温度下钻头对岩石的切削过程，依据PDC钻头切削齿的破碎比功对钻井参数提出了优化建议；LI等[12]揭示了气体钻井过程中热效应对岩石切削的重要影响；ZHANG等[13]采用有限元方法对全尺寸PDC钻头破岩过程的热-结构耦合进行了数值模拟，分析了PDC钻头切削齿失效的原因；李晓红等[14]和杨晓峰等[15]认为温度过高是造成PDC钻头切削齿热破坏的主要原因；张丽秀等[16]采用二维平面模型分析了单齿破岩过程中温度场的分布规律。

上述研究大多基于实验手段和二维平面模型[17]研究切削过程中的温度分布规律。在经济上，数值仿真相比实验有着巨大的优势，二维仿真模型忽略了切削齿侧向与岩石的接触与温度传递，不能得到切削齿整体的温度分布规律。因此，本文基于传统的正交切削理论和岩石的弹塑性力学，以德鲁克-普拉格（Drucker-Prager）模型作为岩石的塑性阶段的屈服本构模型，建立了三维耦合温度场-位移场的PDC钻头切削齿动态破岩的非线性动力学切削数值仿真模型，分析切削齿温度分布规律和切削力的大小，以期得到不同的切削参数、结构参数等因素对切削力和破岩过程中温度传递的影响规律，揭示实际切削齿的动态破岩特性。

1 三维切削数值模型的建立

1.1 PDC钻头切削齿与岩石相互作用模型

首先，作如下假设：①PDC钻头切削齿为刚体，忽略切削过程中切削齿的磨损，仅考虑温度的传导；②岩石考虑为均质的、各向同性的材料；③不考虑牙齿随钻头的随机振动以及钻井液对切削的影响；④删除切削过程中变形达到一定量的岩石单元，模拟岩石在切削齿的作用下脱离井底的过程，忽略删除的岩石单元对后续破岩的影响。

在切削破岩过程中，跟随钻头旋转的切削齿不仅在钻头轴线方向侵入井底岩石，在横向方向也在挤压刮切岩石，迫使接触区域内的岩石发生弹塑性变形。在纵向冲击与横向刮切的耦合作用下，接触区域的岩石从井底脱落。切削齿与岩石相互作用产生的摩擦力会产生热量，导致切削齿和井底岩石的温度升高。为得到破岩过程中的温度场，选取图1（a）中的钻头上的单齿（图1（b））与岩石发生相互作用的耦合温度场进行破岩仿真。

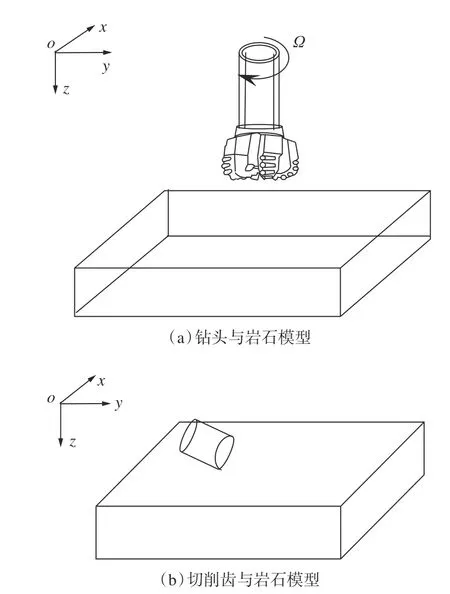
图1 切削模型Fig. 1 Cutting model

切削齿在破岩过程中主要受到摩擦力和支持力作用，基于传统正交切削理论，力学分析时可进一步简化为二维切削模型[18]，如图2所示。

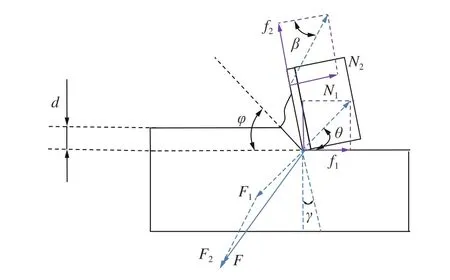
图2 切削齿受力模型Fig. 2 Force model of cutter

切削合力可以表示为式（1）。

将切削合力，沿平面正交分解，可得到主切削力和切深抗力，则有式（2）。

F2主要用于克服岩石的剪切变形[19]，计算见式（3）。

式中：φ为岩石的剪切角，（°）；τs为剪切应力，Pa；l为切削宽度，m；h为切削深度，m；β为前刀面摩擦角，（°）；γ为切削齿的前倾角，（°）。

根据Merchant公式[20]，前刀面摩擦角计算见式（4）。

由库伦摩擦定理可知，后刀面受到的摩擦力计算见式（5）。

作用在前刀面上的剪切力Fs[18]计算见式（6）。

破岩过程中，岩石的变形可分为两个阶段：弹性变形阶段和塑性变形阶段。用线弹性模型来建立岩石在弹性变形阶段的本构，岩石的塑性变形阶段采用德鲁克-普拉格（Drucker-Prager）模型[21-23]，其表达式见式（7）。

式中：I1为应力第一不变量；J2为应力偏量第二不变量；a、K为与岩石材料相关的常数，各项表达式[24]见式（8）。

式中：σx、σy、σz为正应力，Pa；τyz、τxz、τxy为剪应力，Pa；c为岩石内聚力，Pa；φ为岩石内摩擦角，（°）。

岩石的破坏方式主要是剪切破坏[24]，可利用损伤变量D描述塑性单元损伤程度，当岩石等效塑性应变达到时，单元完全失效，从数值模型中实现岩屑的剥离，得到式（9）。

1.2 温度模型

基于传热定律和能量守恒定律，可以建立PDC钻头切削齿与岩石传热分析问题的控制方程[25]，PDC钻头切削齿和岩石的瞬态温度场应满足式（10）。

式中：ρ为材料密度，kg/m3；cr为材料比热容，J/（kg·k）；kx、ky、kz分别为沿x方向、y方向、z方向的传导系数，W/（m·K）；Q为热源强度，W/kg。

切削齿在单位时间内产生热量Q′计算见式（11）。

式中，v为切削速度，m/s。

切削过程中产生的热量传导平衡式，见式（12）。

式中：Q1为切削掉的岩屑携带的热量，J；Q2为岩石携带的热量，J；Q3为切削齿携带的热量，J。

1.3 数值模型

为简化仿真数值模型，建立了PDC钻头切削齿与岩石的三维数值模型，如图3所示。将切削齿的实际运动分解到两个正交的方向。有限元模型中，岩石的大小为0.40 m×0.10 m×0.02 m，PDC钻头切削齿的大小为Φ 0.013 m×0.008 m，WC基体的厚度为0.007 m。岩石和切削齿均采用八结点热耦合六面体减缩积分单元C3D8RT，局部细化了岩石与切削齿发生相互作用的区域，分别划分了440864个单元和17640个单元，如图3所示。其余参数见表1。

表1 材料参数Table 1 Parameters of material

图3 三维单齿切削破岩数值模型Fig. 3 Three-dimensional numerical model of rock-breaking of a single cutter

对切削齿施加刚体约束，采用参考点的位移代替切削齿的位移，不考虑切削齿的应变和应力。添加岩石与切削齿之间的接触，摩擦系数设置为0.30。岩石围压为30.00 MPa，底部采用固定约束，约束切削齿的y-z的平动自由度和x-y-z方向的旋转自由度，保留x方向的平动自由度，速度设置为0.80 m/s。岩石的摩擦角为44.47°，膨胀角为30.00°，切削齿的前倾角为10.00°，切削深度为0.003 m。模型初始温度为100.00°，仿真总时间为0.50 s，时间步长为0.0001 s，仿真计算稳定且可以收敛。

2 仿真结果分析

基于上述计算参数和数值模型，模拟了PDC钻头切削齿在不同工况下的破岩过程，得到了切削力合力和切削齿上温度的分布。图4为当切削深度为0.003 m、切削速度为0.80 m/s时，切削力随时间变化的曲线，与文献[23]得到的切削力变化规律、波动幅值和均值吻合较好。图5为不同时刻下切削过程中岩石的应力分布，PDC钻头切削齿刮切岩石单元使其发生弹塑性变形，当岩石单元应力与塑性应变达到其失效所对应的极限值时，单元失效被破坏，脱落岩石本体，形成孔眼。图6为不同时刻切削过程中岩石与PDC钻头切削齿的温度分布，与文献[8]得到的切削齿上的温度分布规律一致。热量在切削齿与岩石接触表面传递，向内部扩散，最高温度出现在岩石与切削齿的接触区域的最低位置处，即切削刃的中部，切削刃的中部附近区域为切削高温区，然后向两侧温度降低。摩擦产生的热量主要在PDC层上传导，WC基体上温度变化不显著。

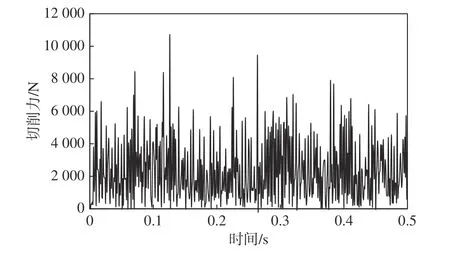
图4 切削力随时间变化曲线Fig. 4 Cutting force changed with time

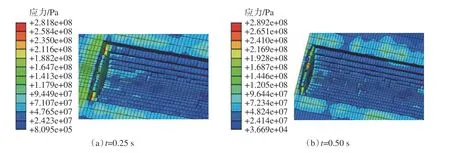
图5 切削过程中岩石的应力分布Fig. 5 Stress distribution of rock during cutting process

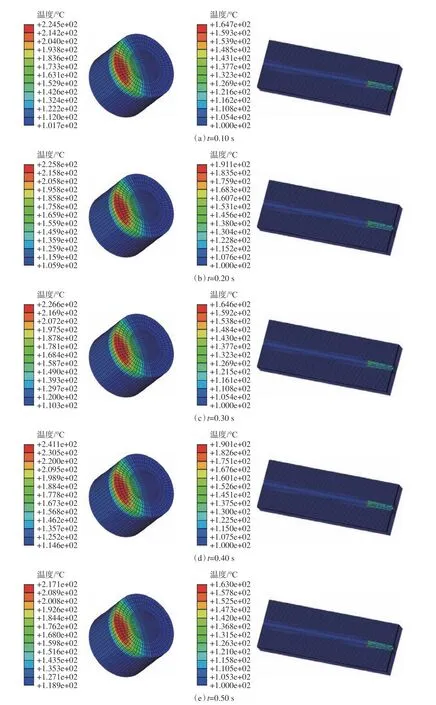
图6 切削过程中岩石与PDC钻头切削齿的温度分布Fig. 6 Temperature distribution of rock and PDC bit cutters during cutting process

2.1 切削深度对切削力和温度的影响

图7为当切削速度为0.80 m/s、齿前角为10.00°时，不同切削深度条件下，随时间变化的切削力曲线。由图7可知，随着切削深度的增加，切削齿与岩层的接触面积增加，剥离岩屑所需的切削力的瞬时最大值、均值和波动幅值急剧增加。切削力的均值分别为681.17 N、1391.22 N、2315.51 N、3568.53 N和4809.79 N。当切削深度为0.005 m时，切削齿所需的切削力是切削深度为0.001 m时切削力的7.06倍。实际钻进时，切削深度过大，导致钻头受到的冲击力变大，更易损坏钻头。

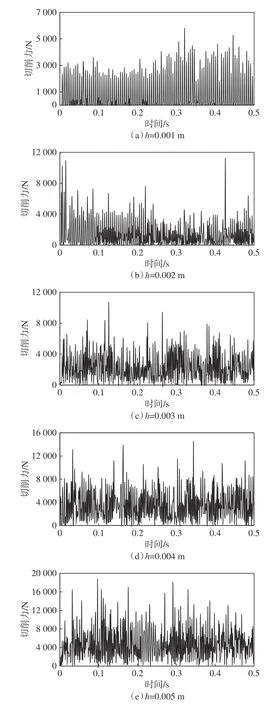
图7 不同切削深度下PDC钻头切削齿的切削力随时间变化曲线Fig. 7 Cutting force of PDC bit cutters changed with time at different cutting depth

图8为当切削速度为0.80 m/s、齿前角为10.00°时，不同切削深度条件下，切削齿与岩层的主要接触面平均温度分布曲线，其中d为距离轮廓线的距离。随着切削深度的增加，单位时间切削的岩屑增加，切削齿与岩石的接触面积增加，摩擦产生的热量变大，切削齿温度上升的范围扩大，温度的梯度显著减小。温度的平均最大值分别为154.67 °C、199.51 °C、222.10 °C、241.38 °C和257.26 °C，平均温度上升速率减缓。当切削深度为0.005 m时，切削齿的最高温度是切削深度为0.001 m时最高温度的1.66倍。当切削深度为0.001 m时，高温分布位置为以切削刃为中心的90°范围，角度为0°～45°、315°～360°；当切削深度为0.005 m时，温度上升显著的位置为以切削刃为中心的230°范围，角度为0°～118°、248°～360°，高温分布的区域显著增大。

图8 不同切削深度下PDC钻头切削齿与岩石的主要接触面上的温度分布变化曲线Fig. 8 Temperature distribution of main contact surface between PDC bit cutters and rock at different cutting depth

2.2 切削速度对切削力和温度的影响

图9为当切削深度为0.003 m、齿前角为10.00°时，不同切削速度条件下，随时间变化的切削力曲线。随着切削速度的增加，切削力的均值分别为2082.37 N、2006.23 N、1990.44 N、2315.45 N和2325.94 N，呈先减小后增大的趋势，切削速度总体对切削力的影响不显著。

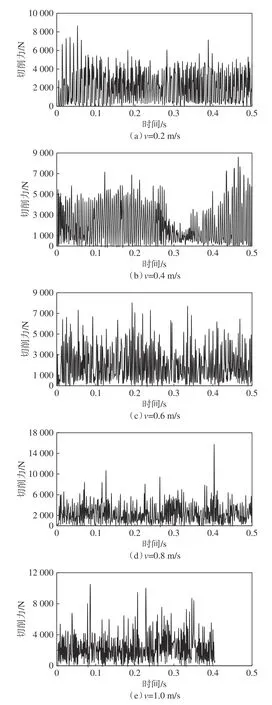
图9 不同切削速度下PDC钻头切削齿的切削力随时间变化曲线Fig. 9 Cutting force of PDC bit cutters changed with time at different cutting speed

图10为当切削深度为0.003 m、齿前角为10.00°时，不同切削速度下，切削齿与岩层的主要接触面平均温度分布曲线，其中d为距离轮廓线的距离。温度的平均最大值分别为171.59 °C、212.63 °C、231.64 °C、222.10 °C和229.01 °C。当切削速度为0.20 m/s时，0.50 s时间段切削齿的移动距离为0.10 m，相比高速（0.60～1.00 m/s）运动的切削齿，其运动较缓慢，散热性较好，温度更低。当切削齿的切削速度为0.40～1.00 m/s时，速度对温度均值的影响较小，影响显著的是齿面的温度梯度和齿面高温区域分布的角度，切削速度越大，温度梯度越小，高温区的角度范围越大。以200.00°为界线，当速度为0.20 m/s时，高温区分布的角度为0°～28°、332°～360°；当速度为1.00 m/s时，高温区分布的角度为0°～39°、321°～360°，增加了22°的分布范围。

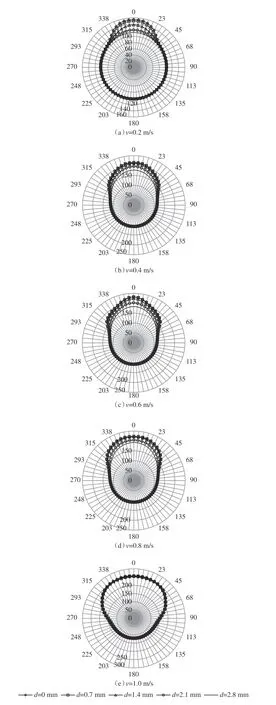
图10 不同切削速度下PDC钻头切削齿与岩石的主要接触面上的温度分布变化曲线Fig. 10 Temperature distribution of main contact surface between PDC bit cutters and rock at different cutting speed

2.3 前倾角对切削力和温度的影响

图11为当切削速度为0.8 m/s、切削深度为0.003 m时，不同前倾角下，随时间变化的切削力曲线。切削力的均值分别为2752.22 N、2271.15 N、2315.51 N、2516.48 N、2523.61 N和2910.03 N，呈现先减小后增大的趋势。在刀具前倾角为7.5°时，得到的切削力最小，可降低切削齿的磨损，最小化切削力。

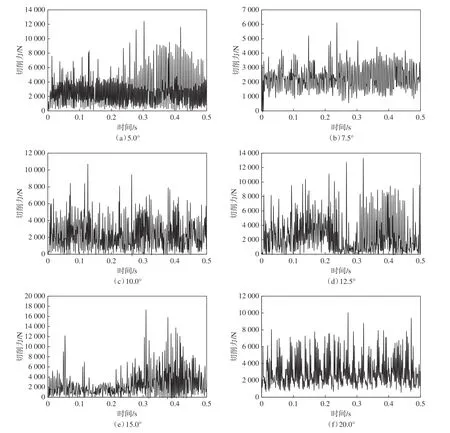
图11 不同前倾角下PDC钻头切削齿的切削力随时间变化曲线Fig. 11 Cutting force of PDC bit cutters changed with time at different rake angle

图12为当切削速度为0.80 m/s、切削深度为0.003 m时，不同前倾角下，切削齿与岩层的主要接触面平均温度分布曲线。温度的平均最大值分别为154.91 °C、176.63 °C、222.10 °C、232.32 °C、225.72 °C和201.67 °C，呈现先增后减小的趋势，较小的倾角下切削齿的温度较低，综合考虑切削力和温度，切削齿的前倾角优选7.5°，可以避免切削齿的高温失效，最小化切削齿面的温度。

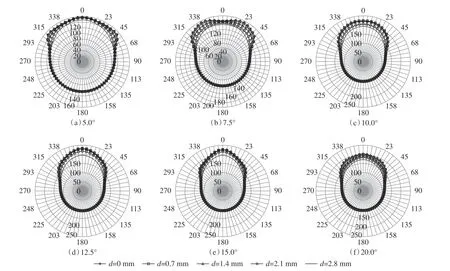
图12 不同前倾角下PDC钻头切削齿与岩石的主要接触面上的温度分布变化曲线Fig. 12 Temperature distribution of main contact surface between PDC bit cutters and rock at different rake angle

3 结 论

基于正交切削模型建立耦合温度-位移场的三维PDC钻头切削齿切削数值模型，模拟切削齿切削过程中的动态力学特性和温度分布规律。分析不同工况参数对切削力和温度的影响，得出结论如下所述。

1）热量在切削齿与岩石接触表面传递，向内部扩散，切削齿的高温区为切削刃附近的椭圆区域，最高温度出现在切削刃的中部。

2）切削深度越大，切削力瞬时最大值、均值和波动幅值、高温分布区域的范围越大，最高温度越大，温度梯度越小。切削深度为0.001～0.005 m时，高温分布位置为以切削刃为中心的90°区域，切削深度为0.005 m时，切削力增加7.06倍，最大温度增加1.66倍，高温区角度增至230°，切削深度应优选0.001 m。

3）切削速度对温度和切削力的均值影响较小。

4）切削齿的前倾角为7.5°时，切削力和最高温度最小。