圆柱滚子轴承滚子对数修形优化研究*

吕海霆,郭玉飞,魏延刚,3,许 凯,姚金池

(1.大连科技学院 机械工程学院,辽宁 大连 116052;2.瓦房店轴承集团有限责任公司,辽宁 瓦房店 116300;3.大连交通大学 机械工程学院,辽宁 大连 116028)

0 引 言

直母线滚子轴承的滚动体与滚道间的早期接触疲劳点蚀常常发生在滚子或滚道上靠近滚子端部的区域,这是因为直母线滚子轴承在受载后,其滚动体两端不可避免地存在边界应力集中,即所谓的“边缘效应”。“边缘效应”的产生使滚子和滚道上靠近滚子端部区域的应力大大超过滚子中部的应力值,使轴承的疲劳寿命大大降低。

为了克服这种“边缘效应”,国外学者LUNDBERG G等人[1-7]进行了大量的理论分析和实验研究。早在19世纪30年代末,LUNDBERG G就提出了母线修形的基本理论。至20世纪60年代,SKF轴承公司进一步发展了滚子轴承的修形技术。

国内开始研究滚子轴承的修形理论和技术大约是在1992年前后[8-12]。马家驹[8]最先开展了滚子凸度设计研究,代风云[9]介绍了国外提高圆柱滚子轴承寿命的途径。随后,陈晓阳等人[10-12]也进行了对数型滚子凸度量和寿命关系的研究。在2000年之后,国内各大骨干轴承企业开始陆续引进了进口的滚子轴承超精研设备,工程技术人员和学者也发表了不少关于滚子类轴承修形理论和技术的论文[13-21]。例如,魏延刚等人[13-16,20-21]应用有限元法对偏载时滚子的非对称修形、圆柱滚子和圆锥滚子的对称修形和非对称修形等滚子类轴承相关修形理论和技术开展了研究。王彦伟等人[17-19]也先后对圆锥滚子轴承的修形进行了研究。

可以说,目前我国轴承行业已经充分掌握了滚子类轴承的修形理论和技术,修形理论与技术都非常成熟;对数修形效果最佳,已成为滚动轴承界的共识。然而,关于滚子类轴承修形的优化设计还需要深入研究。以前由于计算手段的局限,滚子类轴承修形往往是以轴承的最大接触应力最小为优化目标,其理论根据为LUNDBERG G[1]提出的轴承寿命与应力的7次方成反比。随着“切片法”基本思想的出现,《滚动轴承常规载荷条件下轴承修正参考额定寿命计算方法:发展草案ISO/TS 16281:2008》,即Rolling Bearings-Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings:Draft for Development DD ISO/TS 16281:2008[22]给出的轴承修正参考额定寿命计算推荐方法采用了“切片法”的基本思想,引入了切片模型来计算任意滚子的任意切片的弹性变形,这样就使得滚子类轴承疲劳寿命的计算包括了母线类型的影响因素。也就是说,滚子与套圈接触的母线类型对疲劳寿命的影响可直接计算,从而使得滚子类轴承的修形可以以轴承的疲劳寿命最长为优化目标进行优化设计。

虽然,轴承的最大接触应力越小,轴承的疲劳寿命越长;但是以轴承的最大接触应力最小为优化目标和以轴承的疲劳寿命最长为优化目标所求得的最佳修形量是否相同,这还需要进一步研究。为此,笔者拟采用Romax Designer工程分析软件,根据ISO/TS 16281:2008的计算方法,对某大兆瓦风电机组齿轮箱输出轴圆柱滚子轴承的对数修形优化进行较深入的研究。

笔者应用Romax Designer工程分析软件分析多个工况,即多组轴承工作径向游隙情况下,多组内外圈相对倾斜量情况下,以及不同修形量时的轴承载荷分布、接触应力、滚动体修形效果和疲劳寿命;累计计算60多个方案。在此,为了节省篇幅,仅给出额定载荷工况下的几组典型计算结果来探讨不同径向游隙、不同内外圈相对倾斜量情况下滚子的修形效果,并比较以轴承的最大接触应力最小为优化目标和以轴承的疲劳寿命最长为优化目标所求得的最佳修形量,为滚子类轴承的修形优化设计提供参考。

1 DD ISO/TS 16281:2008圆柱滚子轴承修正参考额定寿命简析

文献[22]的引言如下:

“自1990年发布ISO 281以来,已经获得了关于来污染、润滑、安装内部应力、硬化应力、材料疲劳载荷极限等对轴承寿命的影响的更多知识。因此,现在可以在寿命计算中更全面地考虑影响轴承寿命的因素。

ISO 281:2007提供了一种方法,在计算轴承的修正额定寿命时,以一致的方式将这一新知识付诸实践。然而,ISO 281:2007中给出的计算方法不能考虑倾斜或错位对轴承寿命的影响,以及运行期间轴承游隙对寿命的影响。本技术规范描述了一种先进的计算方法,该方法还可以考虑这些影响,从而为估算污染和其他因素的影响提供最准确的支持。”

也就是说,ISO/TS 16281:2008不仅考虑了国际标准滚动轴承—额定动载荷和额定寿命ISO 281:2007,即Rolling Bearings-Dynamic Load Ratings and Rating Life:International Standard ISO 281:2007(E)[23]中涵盖的各因素,还考虑了轴承套圈相对偏斜、轴承工作游隙和其他影响轴承内部载荷分布的因素等。另外,文献[22]的特点还在于更为准确地计算了轴承内部载荷分布情况,特别是对滚子类轴承,引入了切片模型来计算任意滚子的任意切片弹性变形。

圆柱滚子轴承修正参考额定寿命的计算公式如下[22]：

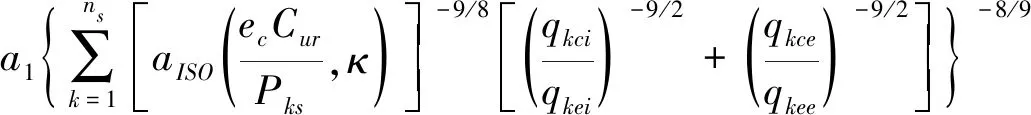
(1)

式中:Pks为轴承层k的当量动载荷;Lnmr为轴承修正参考额定寿命;a1为可靠性寿命修正系数;ec为润滑剂污染系数;κ为黏度比;qkci,qkce为内圈和外圈轴承层的基本额定动载荷;qkei,qkee为内圈和外圈的k层切片上的当量动载荷;Cur为疲劳载荷极限;aISO为寿命修正系数。

Pks表达式如下[22]：

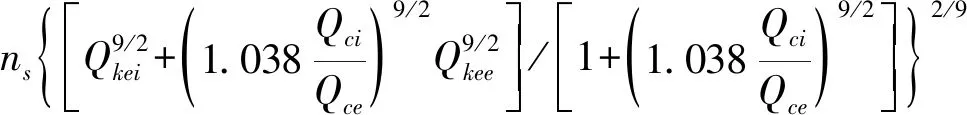
(2)

式中:Qci,Qce为内圈和外圈的基本额定动态载荷,分别由qkci,qkce求和而得;Qei,Qee为内圈和外圈滚道当量动载荷,分别由qkei和qkee求和而得。

其中:各参数的物理意义可参见文献[22]和文献[23]。通过对文献[22]和文献[23]的分析可知,ISO/TS 16281:2008给出圆柱滚子轴承修正参考额定寿命Lnmr是可靠性寿命修正系数a1的线性函数;是润滑剂污染系数ec和黏度比κ、内圈和外圈轴承层的基本额定动载荷qkci和qkce(或者内圈和外圈的基本额定动态载荷Qci和Qce)、内圈和外圈的k层切片上的当量动载荷qkei和qkee(或者内圈滚道当量动载荷Qei和外圈滚道当量动载荷Qee)、轴承层k的当量动载荷Pks、疲劳载荷极限Cur和寿命修正系数aISO的非线性复杂函数。而且a1、κ、ec、qkci和qkce以及Cur和aISO越大;Pks、qkei和qkee越小;则修正参考额定寿命Lnmr越长。

此外,轴承径向游隙、内外圈相对倾斜(或者说错位)和滚动元件修形通过内圈和外圈的k层切片上的当量动载荷qkei和qkee(或者内圈滚道当量动载荷Qei和外圈Qee滚道当量动载荷)、轴承层k的当量动载荷Pks、Cur和寿命修正系数aISO影响修正参考额定寿命Lnmr。

2 不同径向游隙情况下对数修形

此处以某大兆瓦风电机组齿轮箱高速输出轴轴承为例。该轴承为圆柱滚子轴承,其基本代号为NU2332,基本参数为:轴承内径160 mm,轴承外径340 mm,轴承宽度114 mm,滚子数目14,滚子直径40 mm,滚子长度65 mm,内圈滚道直径228 mm,外圈滚道直径308 mm。

所研究的轴承滚动体和内、外圈的弹性模量取205 GPa,泊松比取0.3,热膨胀系数取12×10-61/℃。

首先,笔者介绍轴承径向载荷为额定载荷65 kN,滚子和内、外圈的接触轮廓均为直母线(即滚子和内、外圈滚道均未修形),轴承内圈相对外圈倾斜量γ为0.175 6 mrad,轴承工作时的径向游隙s分别为0.027 4 mm、0 mm和-0.027 4 mm时,轴承载荷分布、接触应力和ISO/TS 16281的寿命情况。

在载荷一定的情况下,由于滚动轴承的内部载荷分布主要取决于轴承的径向游隙,而轴承内外圈相对倾斜和对数修形虽然对轴承承载的滚子数目影响不大,但是影响其接触应力的分布;同时,计算结果也表明,在所设定的轴承内外圈相对倾斜量情况下,无论是否修形,在65 kN的径向载荷作用下,轴承工作径向游隙s为0.027 4 mm、0 mm和-0.027 4 mm时,参预承载的滚子数目分别为5、7和14。因此,在不同内外圈相对倾斜量情况下,无论是否修形,轴承的滚子与套圈滚道接触力分布图和最大接触应力图都相似,只是具体数值不同[24];而Romax Designer采用沿套圈滚道周向分布图(也称雷达图)来表达滚道接触力分布和最大接触应力分布。

套圈滚道最大接触应力分布图如图1所示。

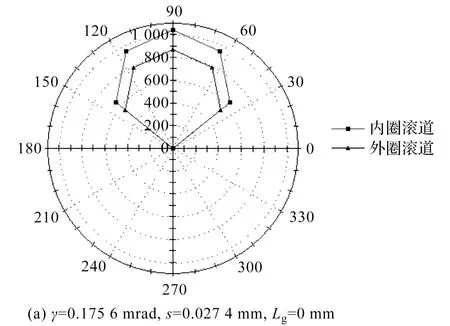
图1 沿周向接触应力分布图

滚子与内圈滚道间接触应力云图如图2所示。

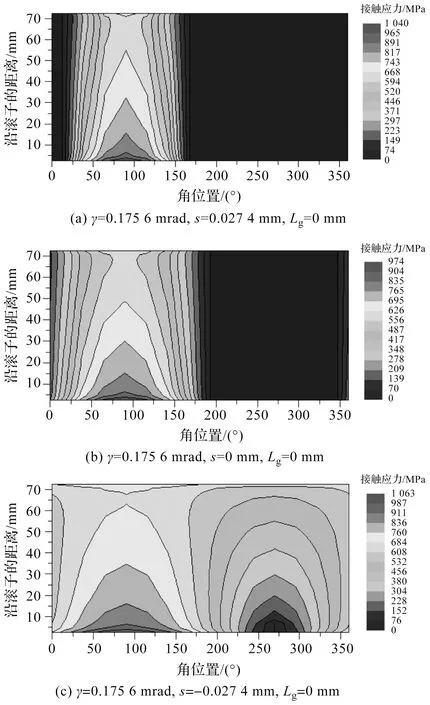
图2 滚子与内圈滚道间接触应力云图

然而,滚子与套圈滚道接触应力沿滚子轴向和沿套圈滚道周向的分布,以及滚子与套圈滚道最大接触应力沿滚子母线的分布,不仅与轴承工作径向游隙有关,而且还与内外圈相对倾斜量和修形量相关。

图2中,Romax Designer用在滚子轴向和滚子位置角构成的平面上的接触应力云图表达接触应力沿子轴向和套圈滚道周向的分布。

滚子与内圈滚道接触应力沿滚子接触母线分布曲线如图3所示。

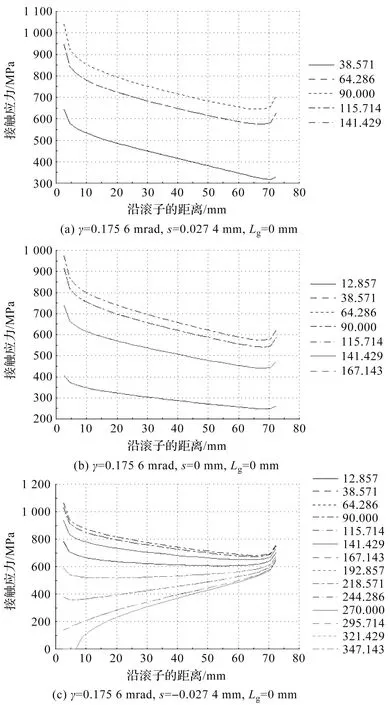
图3 滚子与内圈滚道接触应力沿滚子接触母线分布曲线

由于滚子与内圈滚道间的最大接触应力大于滚子与外圈滚道间的最大接触应力,因此,在此仅给出未修形时滚子与内圈滚道间的触应力云图(见图2)和最大接触应沿滚子母线分布曲线图(见图3)。

对数修形影响滚子与滚道接触应力沿滚子轴向和沿滚道周向的分布和滚子与滚道最大接触应力沿滚子母线的分布,而滚子与滚道最大接触应力沿滚子母线分布曲线图更能形象地反映修形效果。

为节省篇幅,笔者在此仅给出一组修形滚子与内圈滚道间最大接触应力沿滚子母线的分布曲线图,如图4所示。

图4 滚子与内圈滚道接触应力沿滚子接触母线分布曲线图

图1、图2和图3分别是未修形(修形量lg=0 mm)时的滚子与套圈滚道最大接触应力沿套圈滚道周向分布图、沿子轴向和套圈滚道周向分布的接触应力云图和滚子与内圈滚道间最大接触应力沿滚子母线分布曲线图。

图4是轴承工作径向游隙s为0.027 4 mm、0 mm和-0.027 4 mm时,所对应的以轴承的ISO/TS 16281疲劳寿命最长为优化目标,最优修形量时的最大接触应力沿滚子母线分布曲线图。

观察图3和图4中的每条曲线对应相应位置角处滚子的接触应力沿滚子接触母线的分布曲线可知:由于内圈相对外圈倾斜,使得接触应力沿滚子母线从一端到另一端由大变小,曲线是倾斜的;

此外,对比图3和图4可知:未修形的滚子两端的接触应力都存在明显的“边缘效应”,即滚子边缘处的应力集中导致滚子边缘的应力突然增加;优化修形消除了滚子两端接触应力的“边缘效应”,最大接触应力大大降低。

不同对凸度量对应的寿命及相关参数(内外圈相对倾斜0.175 6 mrad,工作径向游隙0.027 4 mm)如表1所示。

表1 不同对凸度量对应的寿命及相关参数(内外圈相对倾斜0.175 6 mrad,工作径向游隙0.027 4 mm)

表1中,倒数第二行为以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的各参数与未修形时对应的各参数的相对差百分比;最后一行为以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的各参数与以最大接触应力最小为优化目标的最优修形凸度量对应的各参数的相对差百分比。

另外需要说明的是,除了内外圈相对倾量,随着修形量的增加而单调增加外,其他的量都不是单调变化,要么由大变小再由小变大,要么由小变大再由大变小。但是这些量在某个修形量的范围内可能表现为单调增加或单调减少。

此外,由上节ISO/TS 16281:2008圆柱滚子轴承修正参考额定寿命简析的分析可知:寿命修正系数aISO和疲劳载荷极限Cur越大,内圈滚道当量动载荷Qei和外圈滚道当量动载荷Qee越小,ISO/TS 16281:2008寿命Lnmr越长。

还需要进行说明的是,内圈滚道当量动载荷Qei和外圈滚道当量动载荷Qee分别是由轴承内圈和外圈k层(切片)上的当量动载荷qkei和qkee求和的结果,Romax Designer分析软件提供的计算结果没有qkei和qkee,而是给出内圈滚道当量动载荷Qei和外圈滚道当量动载荷Qee,所以表1中给出了Qei和Qee。

不同对凸度量对应的寿命及相关参数(内外圈相对倾斜0.175 6 mrad,工作径向游隙0 mm)如表2所示。

表2 不同对凸度量对应的寿命及相关参数(内外圈相对倾斜0.175 6 mrad,工作径向游隙0 mm)

不同对凸度量对应的寿命及相关参数(内外圈相对倾斜0.175 6 mrad,工作径向游隙-0.027 4 mm)如表3所示。

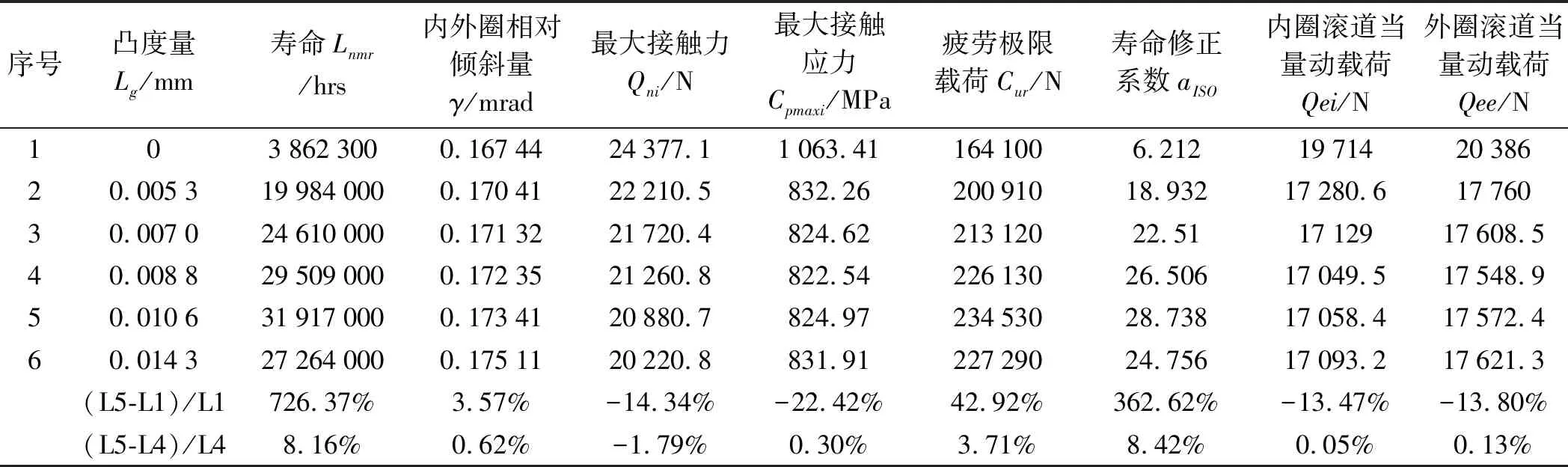
表3 不同对凸度量对应的寿命及相关参数(内外圈相对倾斜0.175 6 mrad,工作径向游隙-0.027 4 mm)

由表1、表2和表3可见:以ISO/TS 16281寿命最长为优化目标的最优修形凸度量Lg分别为0.008 8 mm、0.009 2 mm和0.010 6 mm,以最大接触应力最小为优化目标的最优修形凸度量Lg分别为0.006 1 mm、0.005 3 mm和0.008 8 mm。

与未修形的寿命相比,以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的寿命分别长318.26%、313.95%和726.37%;对应的最大接触应力比未修形的分别小17.96%、17.23%和22.42%。

以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的ISO/TS 16281寿命比以最大接触应力最小为优化目标的最优修形凸度量对应的ISO/TS 16281寿命分别长10.63%、9.71%和8.16%;而以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的最大接触应力比以最大接触应力最小为优化目标的最优修形凸度量对应的最大接触应力分别仅大0.61%、1.18%和0.30%。

由此可见,在不同的径向游隙下,以轴承的疲劳寿命最长为优化目标和以轴承的最大接触应力最小为优化目标所求得的最佳修形量都不同。虽然,相应的最大接触应力相差都很小,但是相应的疲劳寿命相差都较大。

因此,对数修形时应当以轴承的ISO/TS 16281疲劳寿命最长为优化目标。

3 不同内外圈相对倾斜情况下对数修形

为了研究内外圈相对倾斜对轴承寿命和修形效果的影响,笔者在此分析轴承工作径向游隙s为0.027 4 mm,轴承内外圈相对倾斜量分别为0.041 8 mrad、0.175 6 mrad和0.534 6 mrad时,几组修形凸度量所对应的ISO/TS 16281寿命以及与寿命相关的主要参数。

不同对凸度量对应的寿命及相关参数(工作径向游隙0.027 4 mm,内外圈相对倾斜0.041 8 mrad)如表4所示。

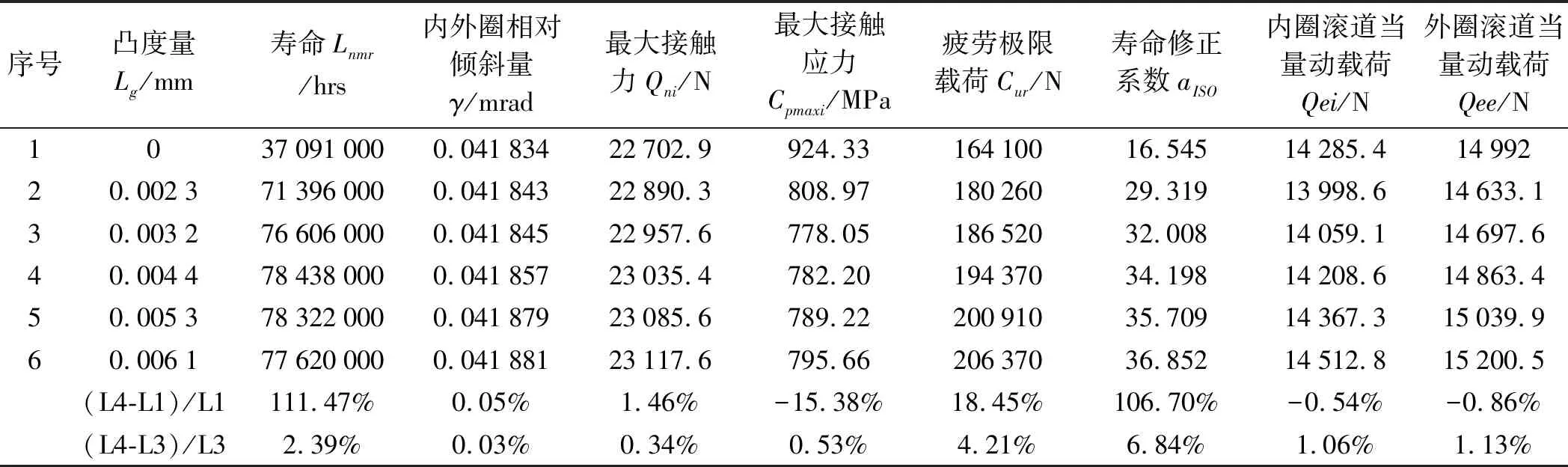
表4 不同对凸度量对应的寿命及相关参数(工作径向游隙0.027 4 mm,内外圈相对倾斜0.041 8 mrad)

不同对凸度量对应的寿命及相关参数(工作径向游隙0.027 4 mm,内外圈相对倾斜0.534 6 mrad)如表5所示。

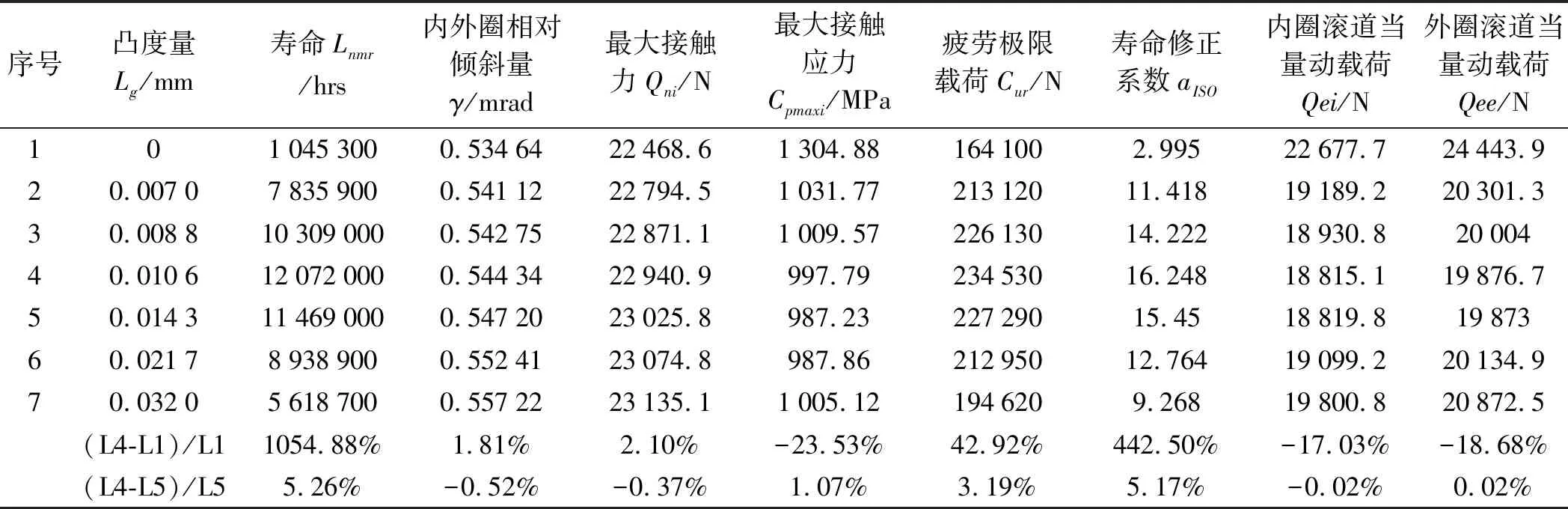
表5 不同对凸度量对应的寿命及相关参数(工作径向游隙0.027 4 mm,内外圈相对倾斜0.534 6 mrad)

由表4、表2和表5可见,以ISO/TS 16281寿命最长为优化目标的最优修形凸度量Lg分别为0.004 4 mm、0.008 8 mm和0.010 6 mm,以最大接触应力最小为优化目标的最优修形凸度量Lg分别为0.003 2 mm、0.006 1 mm和0.014 3 mm。

以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的寿命比未修形的寿命分别长111.47%、318.26%和1 054.88%;对应的最大接触应力比未修形的分别小15.38%%、17.96%和23.53%。

以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的ISO/TS 16281寿命比以最大接触应力最小为优化目标的最优修形凸度量对应的ISO/TS 16281寿命分别长2.39%、10.63%和5.26%;而以ISO/TS 16281寿命最长为优化目标的最优修形凸度量对应的最大接触应力比以最大接触应力最小为优化目标的最优修形凸度量对应的最大接触应力分别仅大0.53%、0.61%和1.07%。

由此可见,在轴承内外圈相对倾斜量不同的情况下,以轴承的疲劳寿命最长为优化目标和以轴承的最大接触应力最小为优化目标所求得的最佳修形量都不同。虽然,相应的最大接触应力相差都很小,但是相应的疲劳寿命相差都较大。

因此,对数修形时应当以轴承的ISO/TS 16281疲劳寿命最长为优化目标。

4 结束语

笔者采用Romax Designer工程分析软件,对某大兆瓦风电机组齿轮箱输出轴轴承在不同径向游隙、不同内外圈相对倾斜量情况下,不同滚子对数修形凸度量时的轴承载荷分布、最大接触应力、轴承疲劳寿命以及与寿命相关的性能参数进行了大量的计算,并对最佳对数修形凸度量进行了分析,从中得到如下结论:

1)在不同的径向游隙下,以轴承疲劳寿命最长为优化目标和以轴承最大接触应力最小为优化目标所求得的最佳修形量都不同,以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命比以最大接触应力最小为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命长很多,而以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的最大接触应力比以最大接触应力最小为优化目标的最佳修形凸度量对应的最大接触应力稍微大一点点。

在笔者所研究轴承的具体条件下,内外圈相对倾斜0.175 6 mrad,轴承工作径向游隙分别为0.027 4 mm、0 mm和-0.027 4 mm时,以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命比以最大接触应力最小为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命分别长10.63%、9.71%和8.16%;而以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的最大接触应力比以最大接触应力最小为优化目标的最佳修形凸度量对应的最大接触应力分别仅增加0.61%、1.18%和0.30%;

2)在不同的轴承内外圈相对倾斜量下,对数修形效果与在不同的径向游隙下的相似。在笔者所研究轴承的具体条件下,轴承工作径向游隙为0.027 4 mm,轴承内外圈相对倾斜量分别为0.041 8 mrad、0.175 6 mrad和0.534 6 mrad时,以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命比以最大接触应力最小为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命分别长2.39%、10.63%和5.26%;而以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的最大接触应力比以最大接触应力最小为优化目标的最佳修形凸度量对应的最大接触应力分别仅增加0.53%、0.61%和1.07%;

3)滚子类轴承对数修形时应当以轴承的ISO/TS 16281疲劳寿命最长为优化目标。

在笔者所研究轴承的具体条件下,内外圈相对倾斜0.175 6 mrad,轴承工作径向游隙分别为0.027 4 mm、0 mm和-0.027 4 mm时,以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命比未修形的ISO/TS 16281寿命分别长318.26%、313.95%和726.37%;轴承工作径向游隙为0.027 4 mm,轴承内外圈相对倾斜量分别为0.041 8 mrad、0.175 6 mrad和0.534 6 mrad时,以ISO/TS 16281寿命最长为优化目标的最佳修形凸度量对应的ISO/TS 16281寿命比未修形的ISO/TS 16281寿命分别长111.47%、318.26%和1 054.88%;

4)计算圆柱滚子轴承的疲劳寿命时一定要考虑径向游隙、轴承内外圈相对倾斜和轴承修形的综合影响;对轴承进行修形优化时,也应当考虑径向游隙、轴承内外圈相对倾斜对修形效果的影响。

笔者目前的研究结果可为滚子类轴承的优化设计提供指导或参考。在以后的工作中,笔者将寻求与相关企业进行合作,以对上述研究结果进行相关的实验验证。