基于IPIO-VME与ConvNeXt-Encoder-GRU的轴承剩余寿命预测*

2024-04-24黄博昊董红涛卫若茜陈敬川

机电工程 2024年4期

黄博昊,董红涛,赵晖,卫若茜,陈敬川,何澳

(1.中国矿业大学 (北京) 人工智能学院,北京 100083;2.陕西彬长小庄矿业有限公司,陕西咸阳 713500;3.陕西彬长矿业集团有限公司,陕西咸阳 712000)

0 引言

轴承是机械设备中至关重要的零部件之一,同时,其健康状态对机械设备的安全可靠运行起着重要作用。

目前,机械设备正向着高速化、大型化、智能化方向发展[1],为了保证生产的高效性、稳定性,对轴承的剩余寿命进行预测具有重要意义。寿命预测技术能够将定期维修转变为预先维修,根据预测报告对设备的故障零部件进行维修和更换,可以节省成本,减少安全事故的发生。

在目前的轴承剩余寿命研究中,存在原始数据噪声较大,特征提取过程复杂的问题,并且剩余寿命模型的构建过程繁琐,需要进行退化特征的筛选,使预测结果存在较大误差。

因此,设计一个自适应的特征模态提取方法和剩余寿命预测模型具有重要的工程意义。

轴承故障信号表现为周期性冲击信号,具有非平稳性,且常有噪声。HUANG E[2]于1998年提出了经验模态分解算法(empirical mode decomposition, EMD),主要应用于非平稳信号;但是该算法还存在着模态混叠和端点效应的问题。GILLES J[3]于2013年提出了经验小波变换(empirical wavelet transform, EWT)方法,它可以自适应地划分频带,并构建小波滤波器组,进而进行了信号的分解。DRAGOMIRETSKIY K[4]构造了变分问题,并对其进行了求解,提出了变分模态分解(variational mode decomposition, VMD)算法。JIANG Xing-xing[5]使用初始中心频率引导的VMD方法,利用中心频率和智能优化算法进行了搜索,匹配了故障相关模式带宽的最佳平衡参数。

EMD存在着模态混叠和端点效应的问题,而EWT和VMD则需要提前确定模态的个数,并且模态选择过程冗杂。因此,笔者使用变分模态提取(variational mode extraction, VME)算法[6],以实现特定模态的提取目的。在模态个数未知但中心频域已知的情况下,VME能够较好地分离特征模态。

为进行自适应的模态提取,笔者使用改进的智能优化算法,配合设计的复合目标函数,进行VME参数寻优,并基于此进行轴承振动信号的去噪和特征提取工作。

对于剩余寿命预测模型的建立问题,LI Nai-peng等人[7]1-2对轴承运作进行了研究,将轴承全寿命周期分为两个阶段,分别进行了建模。吕明珠等人[8]针对轴承早期故障点的确定进行了研究,使用包络谐噪比作为预测起始点的指标。李晓昆[9]使用改进相似模型,进行了采煤机轴承剩余寿命预测。REN Lei等人[10]提取了时域、频域以及时频域信息,并联合这些信息,将其输入到深度自编码器中,对轴承剩余寿命进行了预测。

目前,这些方法主要是通过自主选择多种特征进行全寿命周期模型的构建,但实际上很多特征不能代表退化趋势,因此,需要进行复杂的筛选。

针对这个问题,笔者使用神经网络自适应地提取振动信号的特征,并与较少的自主构建特征联合,进行剩余寿命预测。若使用单一时刻的数据进行寿命预测,因为其中包含噪声,误差较大,所以可以使用一段时间内的数据进行样本的构建。

神经网络的选择对剩余寿命预测模型的构建十分重要。在2017年的《Attention is All You Need》[11]中提出了Transformer模型,并以其为基础发展出多个变种网络,如Vision Transformer(ViT)[12]、Swin Trans-former[13]等,在许多方面超越了传统的网络结构。2022年,由FAIR团队对残差卷积神经网络进行了优化,提出了ConvNeXt[14]网络,利用各类优化策略提升了预测的准确率。

但是笔者提出的联合振动数据与特征曲线方法不适合用单一模型完成构建,输入的两类数据具备不同特点,因此,根据轴承全周期寿命振动数据,笔者选择ConvNeXt网络提取振动特征,并使用Transformer的Encoder结构提取特征曲线的趋势特征,通过GRU网络进行融合。

为自适应地进行特征模态提取和去噪,笔者使用改进的智能优化算法进行VME参数选取。其中,鸽群算法(pigeon-inspired optimization, PIO)[15]具有结构简单、高效准确的特点,但容易陷入局部最优,不适合直接应用于VME的参数选择,因此笔者利用自适应惯性权重、收缩包围机制[16]、莱维飞行[17]等对鸽群算法进行改进,增大随机搜索范围,提升收敛速度。

针对目前剩余寿命模型构建复杂,预测误差较大的问题,笔者自主选取较少的特征,联合神经网络自适应地提取特征,使用ConvNeXt提取振动特征;通过Encoder提取时间步特征,利用GRU进行特征的融合;最后使用XJTU-SY进行实验,验证该模型的准确性。

1 IPIO-VME算法

1.1 改进鸽群算法

鸽群算法是通过模拟鸽子归巢的运动行为,进行全局优化。鸽群算法分为两个阶段,第一阶段由最优鸽子的位置作为主导;第二阶段由较优鸽群的重心作为主导,并且每次迭代会淘汰一半的鸽子。

鸽群算法具有计算简单、速度较快的特点,但是容易陷入局部最优。改进鸽群算法(IPIO)通过自适应惯性权重、收缩包围机制和莱维飞行等策略,提高收敛速度,增大随机搜索范围,避免陷入局部最优。

1.1.1 第一阶段

改进的鸽群算法主要分为两个阶段,第一个阶段是进行大范围搜索。对一定比例的优秀粒子求重心,设适应度最高的前n个粒子位置为[x1,x2,…xi,…xn],则第t次迭代后优秀粒子重心g(t)如下式所示:

(1)

式中:xi(t)为第i个粒子的位置;fitness(xi(t))为第i个粒子的适应度函数值。

第一阶段用两种方式进行搜索,粒子将随机选择一种搜索方式。第一种方式是通过收缩包围机制进行大范围搜索,公式如下:

(2)

V(t+1)=g(t)-A·D-xp(t)

(3)

式中:t为当前迭代次数;A为波动范围;a(t)为范围控制因子,随迭代次数线性下降,控制A的范围,从而控制搜索的范围,使其从大范围搜索转为小范围搜索;N为第一阶段的总次数;D为粒子可以探知的距离;g(t)为优秀粒子的重心;xp(t)为当前粒子的位置;V(t+1)为更新后粒子的速度;r1,r2为[0,1]的随机数。

第二种方式是通过重心、全局最优位置和自适应惯性权重共同确定搜索速度和位置,公式如下:

V(t+1)=wp(t)×V(t)+c1×r3×(Gb-xp(t))+F

(4)

其中:

(5)

(6)

v～N(0,1)

(7)

(8)

(9)

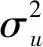
其中,wp(t)根据不同粒子当前的适应度来计算,适应度较高的粒子具有较大的惯性,增加搜索能力;适应度较低的粒子具有较小的惯性,增加收敛速度。

设定粒子惯性权重的上下界如下式所示:

wu(t)=wmin+(wmax-wmin)×(eR(-t+1))

(10)

wd(t)=wmin+(rwmax-rwmin)×(eR(-t+1))

(11)

式中:r为适应度最低粒子的惯性权重衰减比例;wu(t)为当前时刻惯性权重的上界;wd(t)为当前时刻惯性权重的下界;wmin为设定的惯性权重的最小值;wmax为设定的惯性权重的最大值;R为控制惯性权重随代数衰减的速度。

则当前时刻的惯性权重公式如下所示:

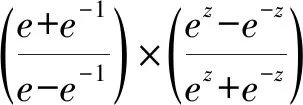
(12)

(13)

式中:fitness(xp(t))为当前粒子的适应度;max(fitness)为当前所有粒子适应度的最大值;min(fitness)为当前所有粒子适应度的最小值。

则第一阶段的整体搜索速度与位置更新公式如下所示:

(14)

xp(t+1)=xp(t)+V(t+1)

(15)

式中:p为[0,1]的随机数;xp(t)为当前位置;V(t+1)为更新后的速度;xp(t+1)为更新后的位置。

1.1.2 第二阶段

第二阶段速度由该粒子自适应惯性权重、优秀粒子的重心、该粒子历史最优位置共同确定。第二阶段的速度更新公式和位置更新公式如下所示:

V(t+1)=wp(t)×V(t)+c2×r4×

(pb-xp(t))+c3×r5×(g(t)-xp(t))

(16)

xp(t+1)=xp(t)+V(t+1)

(17)

式中:r4,r5为[0,1]的随机数;c2为第二阶段个体学习因子;c3为第二阶段社会学习因子;pb为该粒子历史最优位置。

1.1.3 IPIO算法效果测试

为验证IPIO算法的效果,笔者使用单模态和多模态测试函数进行测试。单模态函数具有单峰,主要检验算法的收敛速度;多模态函数具有多峰,主要检验算法的全局收敛能力,体现算法的综合性能。在进行消融实验和对比试验时,可以选用两项指标:1)达到相同精度所用迭代次数;2)相同迭代次数所达到的精度。由于某些算法可能呈现较差的收敛速度和全局收敛能力,长时间迭代都无法收敛至目标精度附近,因此选择指标2),即相同迭代次数所达到的精度。

测试函数、函数的最小值、搜索范围如表1所示。

表1 测试函数、最小值以及搜索范围

每个测试函数的最优位置为x1=x2=…=x30=-1,使最优位置不处于搜索范围中心。

IPIO算法超参数如表2所示。

表2 IPIO超参数以及其值

1)自适应惯性权重与莱维飞行消融实验

为验证自适应惯性权重和莱维飞行的效果,笔者进行了消融实验,将具有自适应惯性权重和莱维飞行的对照算法记为算法A;无自适应惯性权重的算法记为算法B,其中,算法B将自适应惯性权重部分改为所有粒子均使用相同的惯性权重wu(t),即当前时刻自适应惯性权重的上界;将不具备莱维飞行的算法记为算法C。在消融实验中不使用收缩包围机制,迭代1 000次,记录最小值和平均值。

实验结果如表3所示。

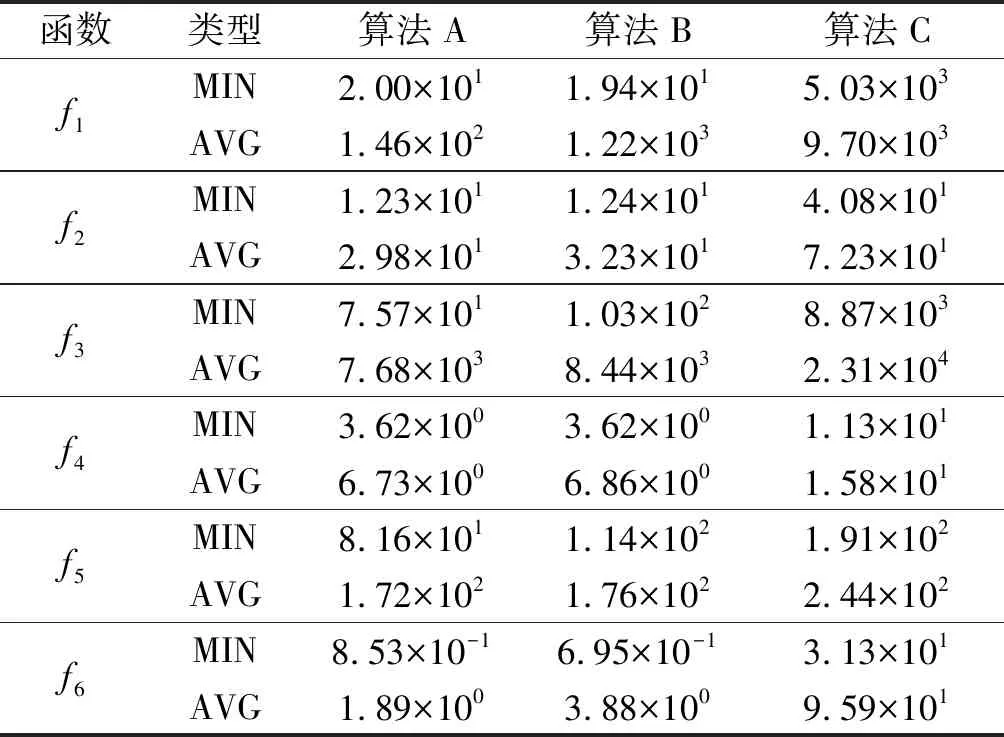
表3 自适应惯性权重及莱维飞行消融实验结果

由表3可知:比较算法A和算法B,在最小值方面算法A和算法B结果较为相近,在平均值方面算法A较算法B更小,平均值能一定程度地消除随机性,体现算法效果,证明自适应惯性权重提升了算法性能;

比较算法A和算法C可知:算法A的最小值和平均值均小于算法C的值,这是由于莱维飞行以优秀粒子重心作为目标,能够综合多个粒子的位置信息;

比较算法B和算法C可知:算法B的最小值和平均值均小于算法C的值,证明莱维飞行对算法性能提升的贡献要高于自适应惯性权重。

2)收缩包围机制消融实验

为验证收缩包围机制的效果,笔者使用IPIO算法作为对照算法,算法D的第一阶段取消收缩包围机制,算法E的第一阶段只使用收缩包围机制,进行1 000次实验,记录最小值和平均值。

结果如表4所示。

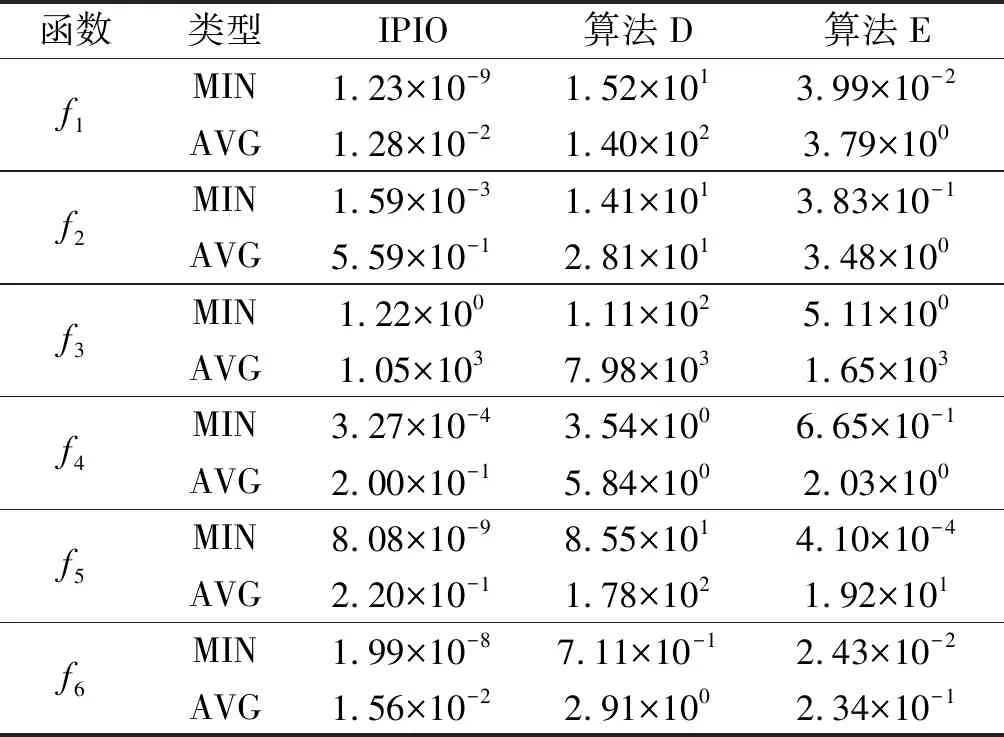
表4 收缩包围机制消融实验结果

由表4可知:IPIO算法相较于只使用单一策略的算法,具备更大的随机性,在单模态函数上测试,平均值和最小值均能取得最小结果,证明IPIO具备较快的收敛速度,能在相同迭代次数下达到最高精度;在多模态函数上测试,平均值和最小值也取得了最小结果,证明IPIO全局收敛能力较好。收缩包围机制会使粒子一定概率地远离目标值,能扩大随机搜索的范围。

可见,IPIO算法兼具较快的收敛速度和较大的随机搜索范围,能够快速收敛至最优值。

3)对比试验

笔者对IPIO算法进行对比试验,每个函数分别使用改进鸽群算法(IPIO)、粒子群算法(particle swarm optimization, PSO)[18]、鸽群算法(PIO)、鲸鱼算法(whale optimization algorithm, WOA)[19]进行搜索,进行迭代1 000次的实验。

记录的最小值和平均值如表5所示。

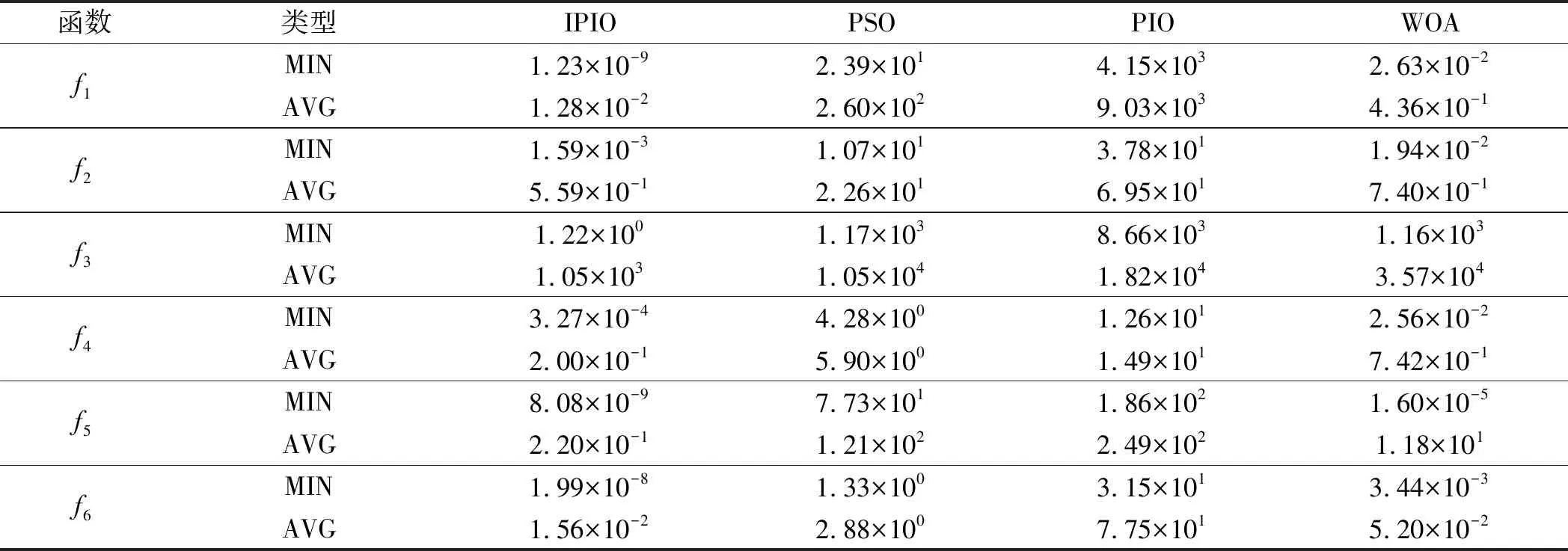
表5 多种智能优化算法1 000次迭代下函数最小值和平均值

6个测试函数的迭代次数和函数值如图1所示。

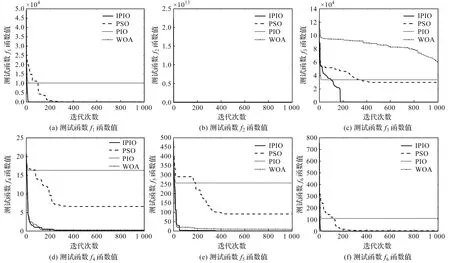
图1 6个测试函数的函数值

由表5和图1可知:在6个测试函数下,IPIO均有较好的表现,1 000次迭代后,在f1、f2、f3三个单模态测试函数下,IPIO算法的最小值和平均值均最小,证明IPIO算法具有较高的收敛速度。

由图1(a)～图1(c)可以看出:IPIO具有较快的收敛速度,局部搜索能力强,能快速收敛到最优值;而PIO在f1和f3函数下难以收敛至理论最优,PSO和WOA算法在f3函数下具有较慢的收敛速度。

1 000次迭代后,在f4、f5、f6三个多模态测试函数下,IPIO的最小值和平均值均优于PSO、PIO、WOA算法的值,且均能收敛至最小值0附近,IPIO具有较高的全局搜索能力。

由图1(d)～图1(f)可以看出:在处理全局搜索问题上,PSO、PIO、WOA算法易陷入局部最优;而IPIO能够在陷入局部最优时,继续搜索,跳出局部最优,具有较强的全局搜索能力。IPIO算法和WOA算法均具备收缩包围机制,但IPIO算法使用了自适应惯性权重和莱维飞行,具有更高的随机性和更快的收敛速度,因此表现较WOA算法更好。

1.2 变分模态提取算法

VME是根据VMD算法原理提出的新算法,使用带宽最小化标准。其带宽估计J1公式如下所示:

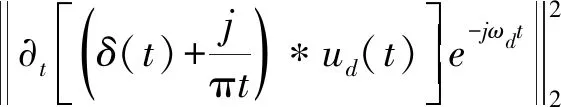
(18)

式中:ud(t)为期望模态;ωd为中心频率;δ(t)为单位冲激函数。

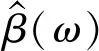
(19)

式中:α为调节带宽因子。

为使ud与残差信号fr的频谱重叠最小,设计罚函数J2公式如下所示:

(20)

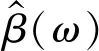
VME通过以下约束最小化来找到期望模态,如下式所示:

(21)

s.t.ud(t)+fr(t)=f(t)

(22)

式中:f(t)为原始信号。

引入二次惩罚项和拉格朗日乘数,如下式所示:

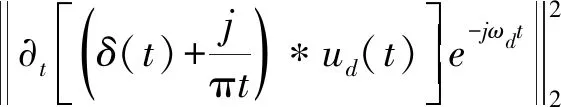
(23)

式中:λ为拉格朗日乘子;“*”为卷积符号。

将函数转为频域,使用交替方向乘子法进行求解,得到ud,ωd,λ的频域表达,迭代更新公式如下:

(24)

(25)

(26)

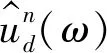
迭代直到满足收敛精度ε,如下式所示:

(27)

1.3 IPIO-VME算法

VME算法最为重要的两个参数值为中心频率ωd和惩罚因子α,利用IPIO算法进行两者的寻优,可以解决人工选择模态的不确定性问题。其关键是选取IPIO的目标函数。

对于轴承的振动信号序列s1…sn,需要考虑以下内容:1)由于VME具有自适应性,所以应要求初始频率尽可能接近收敛中心频率;2)VME提取的信号应尽可能去除噪声,具有较大能量;3)提取的信号应该具有明显特征。

因此,笔者设计的目标函数如下式所示:

(28)

式中:fe为VME算法收敛中心频率;fb为VME算法初始中心频率,同时也是IPIO算法求解的参数。

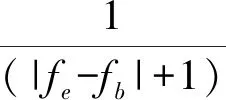
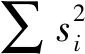
笔者设置迭代次数为100,不同代粒子使用不同颜色进行标注,最终得到了IPIO-VME参数寻优的搜索历史图,如图2所示。

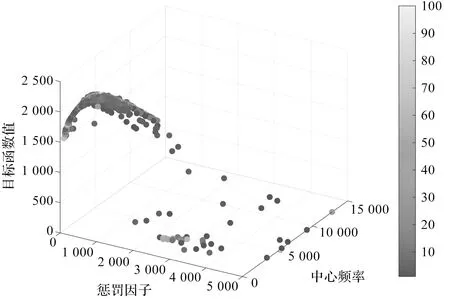
图2 IPIO-VME参数历史搜索图

图2中,在最高点附近具有大量搜索粒子,证明IPIO算法在该任务中具备较好的收敛性能;在IPIO第一阶段(50代前)就可以向最高点附近收敛,且仍具备向随机方向进行搜索的能力。

笔者使用IPIO-VME算法对信号进行处理,以轴承2-4为例,随机截取故障数据的一段振动信号。因轴承故障产生冲击,激起轴承高频振动,所以需要通过求包络进行解调,获得故障特征频率;对该段信号利用希尔伯特变换得到解析信号,并求解析信号的模以获得包络信号,对包络信号进行傅里叶变换,得到包络谱。

轴承2-4故障阶段振动信号的包络谱如图3所示。

图3 原始信号包络谱

对该信号进行IPIO-VME处理后的包络谱如图4所示。

图4 IPIO-VME处理后包络谱

由图3、图4可以看出:原始信号除一倍转频频率、特征频率和其倍频成分外,还包括较多的非特征频率成分;通过IPIO-VME处理后,降低了非特征频率成分,提取出主要特征,提高了特征频率信号的幅值。

2 ConvNeXt-Encoder-GRU模型

2.1 ConvNeXt模块

ResNet[20]网络使用残差链接的方式,解决了网络退化的问题。因此,ConvNeXt模块主要使用残差链接的方式。

ConvNeXt模块如图5所示。

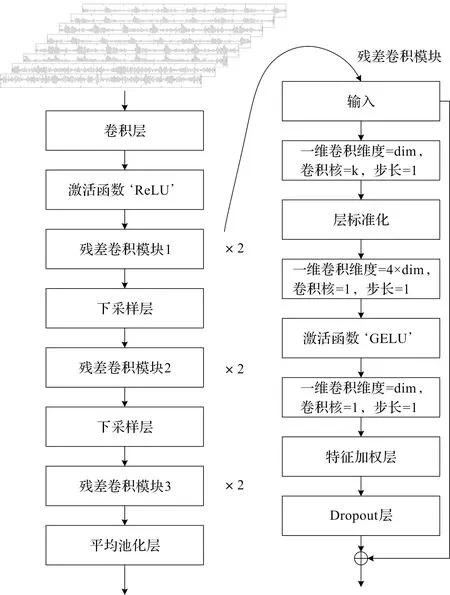
图5 ConvNeXt模块结构图

由图5可以看出:该模块在第一层使用大核卷积以及较大步长以降低长度,后使用多个残差卷积模块和下采样层进行多尺度的特征提取;每个残差卷积模块包括卷积层、层标准化、特征加权层和Dropout层;振动信号数据集的单个样本是包含多个时间步的振动数据,对每一步的振动数据使用多个残差卷积模块和下采样模块进行多尺度特征提取,然后通过平均池化层得出该时间步的多个特征值。

2.2 Encoder模块

Encoder模块主要参考了Transformer模型,用来提取特征曲线的特征。

Encoder模块的结构图如图6所示。

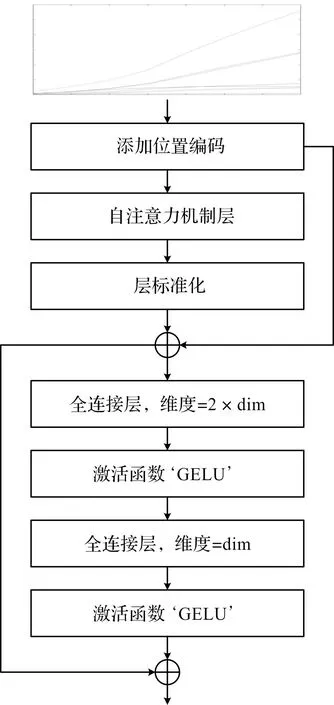
图6 Encoder模块结构图

图6中,由于输入的顺序对结果有较大影响,因此,笔者对输入添加了位置编码,并应用自注意力机制进行特征提取。

2.3 ConvNeXt-Encoder-GRU整体模型

ConvNeXt-Encoder-GRU整体模型包括ConvNeXt模块和Encoder模块。ConvNeXt-Encoder-GRU模型的结构图如图7所示。

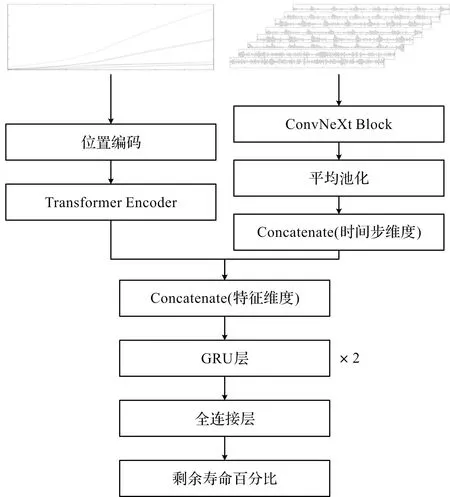
图7 ConvNeXt-Encoder-GRU模型结构图

笔者将ConvNeXt模块提取的特征值按时间步进行拼接;Encoder模块提取特征,然后在特征维度上将其与ConvNeXt模块提取的特征进行拼接,并输入到两层GRU中,通过全连接层进行剩余寿命的预测。

3 算法整体流程

算法整体流程主要分为两个部分,分别是IPIO-VME自适应特征模态提取和ConvNeXt-Encoder-GRU剩余寿命预测。整体算法流程如图8所示。

图8 基于IPIO-VME和ConvNeXt-Encoder-GRU的剩余寿命预测算法

第一部分是信号的预处理和初步特征提取,主要使用改进鸽群算法(IPIO)对VME算法参数寻优,并进行特征模态的提取;第二部分是剩余寿命预测模型的构建,针对全寿命周期的数据,计算时域和频域上的特征,构建两类数据集,分别输入到ConvNeXt-Encoder-GRU模型中,使用ConvNeXt网络提取振动特征,并采用Encoder模型提取趋势特征,通过GRU将二者联合,得到剩余寿命百分比预测结果。

4 实验验证

笔者使用西安交通大学加速寿命试验数据集(XJTU-SY)[21]进行算法的验证。XJTU-SY实验平台由交流电机、转速控制器、测试轴承等组成,通过不同工况下的数据进行加速寿命试验,获取测试轴承全寿命周期的监测数据。

实验平台如图9所示。

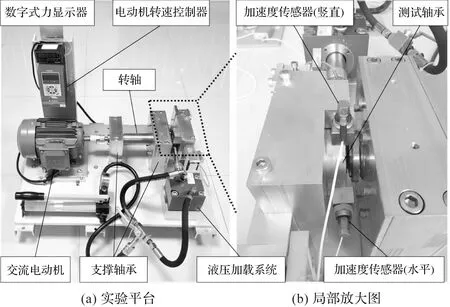
图9 XJTU-SY实验平台

数据集包含3种工况,工况详情如表6所示。

表6 西安交通大学加速寿命数据集工况信息

此处采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。本次实验数据选择工况2下的5个轴承振动数据,分别记为轴承2-1至轴承2-5。

数据集中使用相对法确定轴承的失效阈值,认为振动信号最大幅值超过10×Ah时轴承完全失效。Ah是轴承正常运行阶段的最大幅值,但是利用相对阈值法判断轴承失效时,部分轴承振幅可高达50 g(g是重力加速度),实际生产中会有较大隐患,所以笔者选择使用绝对阈值,根据数据集的振动数据,选择15 g作为失效阈值,当振幅超过15 g时,认为轴承已经失效。

4.1 数据集构建

首先,构建振动信号数据集。

1)从0到轴承失效时,连续8个采样时间点,每个采样时间点随机选取长度为5 000的振动数据;

2)从0到轴承失效时,间隔为1的8个采样时间点,每个采样时间点随机选取长度为5 000的振动数据。

然后,构建特征曲线数据集。

计算每次采集数据的标准差、峰值、峰峰值、上边界、平均绝对值、反正切标准差、频率方差、包络谱最大值;通过稳健二次回归进行平滑处理,并减去平稳运行阶段的均值,构成特征曲线。

1)从0到轴承失效时,连续8个采样时间点,每个采样时间点的8个特征数据;

2)从0到轴承失效时,间隔为1的8个采样时间点,每个采样时间点的8个特征数据。

数据集构建过程如图10所示。

图10 数据集构建示意图

构建的数据集将每个振动数据集和特征曲线数据集按时间一一对应。

对于数据集轴承2-1至轴承2-5,笔者在每个轴承中选择5个振动信号数据,共25个振动数据,对其进行IPIO算法寻优,并取平均值,则VME的σ参数为1 646.9,中心频率为974.2;对数据集的所有振动信号进行VME处理。

4.2 标签处理

笔者使用的模型将轴承全周期寿命分为两部分,一部分是平稳运行阶段,认为这一阶段的剩余寿命百分比为1;另一部分是轴承发生退化到失效的过程,这一阶段是进行剩余寿命预测的阶段[22-23]。

对于寿命预测起始点的确定,笔者选用了均方根(root mean square, RMS)作为指标。根据文献[7]5-7中的3σ原则,选择轴承平稳运行阶段的样本作为基准,计算均值μ和标准差σ;当指标超过平稳运行时的3σ范围,即大于μ+3σ时,则认为产生了早期故障,并将其确定为预测起始点。

确定的寿命预测起始点和失效点如表7所示。

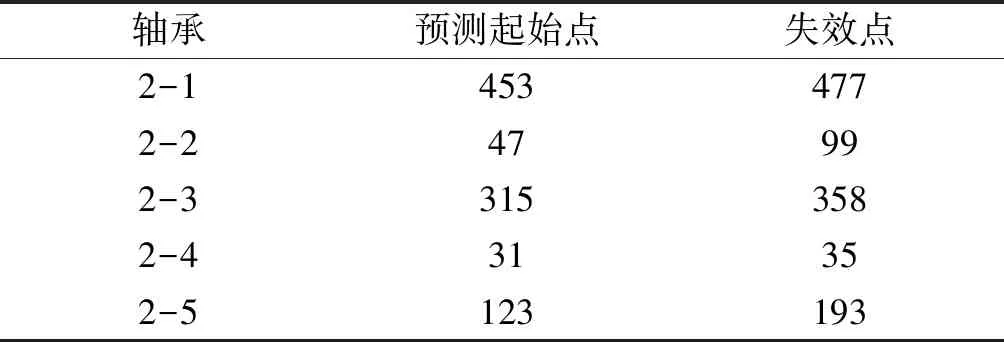
表7 寿命预测起始点和失效点

笔者根据振动数据集样本的最后一个采样时间点确定标签,将最后一个采样时间点在预测起始点前的样本标签设为1;样本最后采样时间点在预测起始点后的,将样本剩余寿命占预测起始点到失效点的寿命长度的百分比作为标签。

设全寿命长度为L,预测起始点为P,振动数据集样本的最后采样时间点为M,则标签RUL如下式所示:

(29)

4.3 对比试验

笔者选择轴承2-1、2-2、2-3、2-4作为训练集,并将轴承2-5作为测试集,进行5次训练,并记录每次结果,计算平均值和最小值;对不分步的ConvNeXt-Encoder-GRU模型、仅有ConvNeXt支路和仅有Encoder支路的模型进行对比实验(不分步ConvNeXt-Encoder-GRU模型指在ConvNeXt模块不进行分步输入,而是通过下采样层和卷积层将数据大小缩减到与Encoder模块输出大小相同);使用双向GRU(bidirectional GRU,BiGRU)进行对比实验。

评价指标选择LogCosh函数,公式如下所示:

(30)

模型的超参数主要根据输入数据的特点进行确定,并通过实验过程不断调整。输入的XJTU-SY数据集样本分为两部分:1)第一部分是连续8个长度为5 000的振动信号;2)第二部分是每个振动信号相对应的自主提取的特征,每个信号提取8个特征。

笔者对第一部分的振动信号使用ConvNeXt模块进行特征提取,为完成从细节到抽象的特征提取任务,在ConvNeXt模型浅层设置大卷积核和较大步长,并设置较多维度,实现细节特征的提取目的;随着层数的增多,减小维度和卷积核的大小,实现抽象特征的提取目的;对第二部分自主提取的特征使用Encoder模块,由于特征的顺序非常重要,因此,在Encoder模块添加位置编码,在每个时间点加上一个权重,并利用Transformer中的自注意力机制进行特征提取。

在实验过程中确定的ConvNeXt-Encoder-GRU模型超参数如表8所示。

表8 ConvNeXt-Encoder-GRU模型超参数表

对比实验的结果如表9所示。

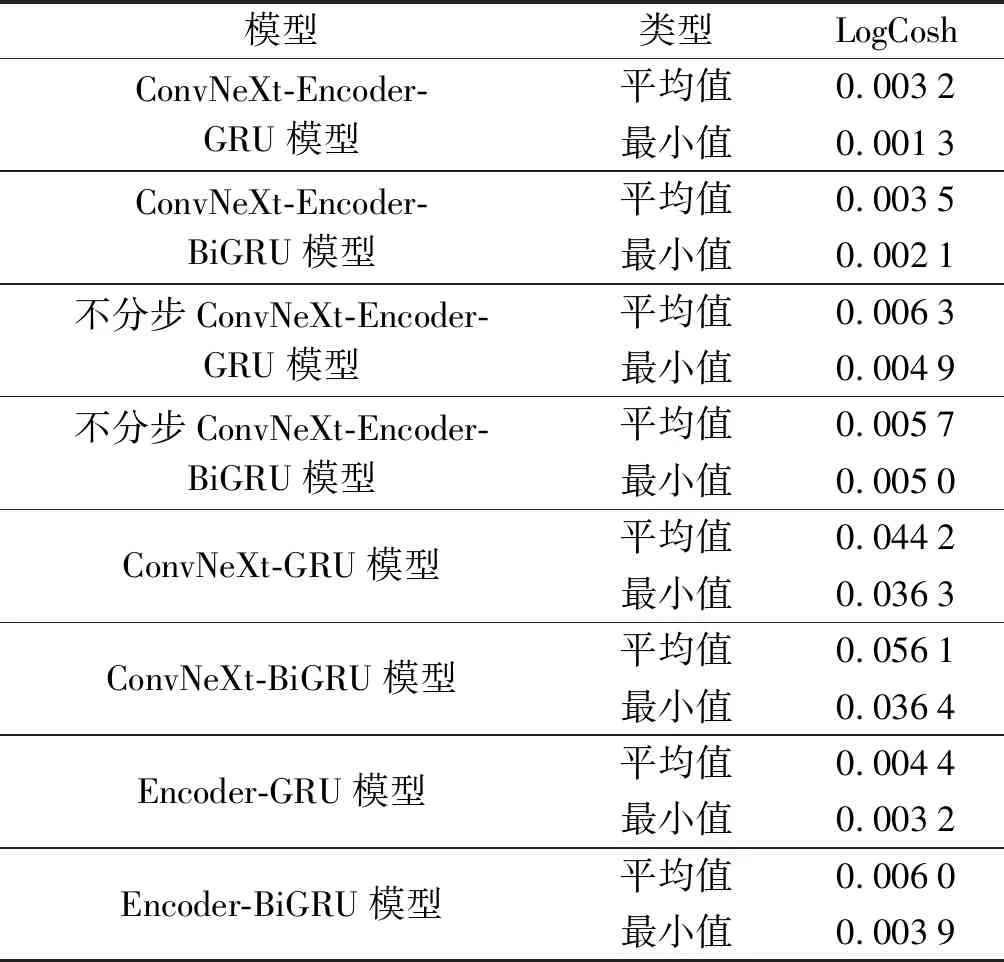
表9 各模型对比实验

笔者使用上述模型对轴承2-5进行全寿命周期预测,预测结果如图11所示。

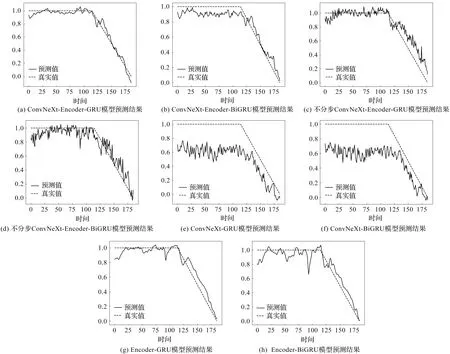
图11 不同模型预测结果

笔者将采用GRU的模型和采用BiGRU的模型进行了对比,可知:采用GRU的模型的LogCosh指标均低于BiGRU的指标,这是由于样本的标签是由样本的最后一个时间步决定,单向GRU更加适合当前寿命预测模型。

笔者将分步的ConvNeXt-Encoder-GRU模型和不分步ConvNeXt-Encoder-GRU模型进行了对比,可知:分步的ConvNeXt-Encoder-GRU预测的曲线更加平滑,这是由于分步的ConvNeXt模块对每一步单独进行了特征提取,保证最后提取到的特征能按照时间步顺序排列;而不分步的ConvNeXt将样本作为一个整体直接输入,损失了时间步的信息,因此预测效果不如分步的模型效果好。

笔者将ConvNeXt-Encoder-GRU模型与ConvNeXt-GRU模型进行对比,可知:由于缺乏特征曲线的信息,ConvNeXt-GRU平滑程度较低,并且其预测效果在平稳运行阶段误差较大。这是由于不同轴承在平稳运行阶段的特征有所不同,而经过处理的特征曲线在一定程度上减少了这些差异。

笔者将ConvNeXt-Encoder-GRU模型与Encoder-GRU模型对比,可知:Encoder-GRU仅使用特征曲线信息,会在某些样本上出现较大误差,这是由于自主提取的特征具有局限性,不能体现轴承的退化特征;而ConvNeXt-Encoder-GRU模型中的ConvNeXt模块,能够自适应地提取振动信号的特征,完成特征的补充工作,并通过GRU模块进行了特征融合,兼具二者的优势。