深井超深井注入过程井筒温度场模型研究及应用

2024-04-24秦彦斌王文波李国亮

石油化工应用 2024年3期

秦彦斌，王文波，李国亮，韦亮

（1.西安石油大学机械工程学院，陕西西安 710065；2.中国石油集团西部钻探公司试油公司，新疆克拉玛依 834000）

目前绝大多数油气藏都需要进行酸化、压裂等方式进行储层改造来提高单井采收率[1]。压裂、酸化时，井筒温度的变化会影响改造液的性能[2]；低温流体的注入会使井筒温度重新分布，产生的温度效应会使管柱承受较大的附加轴向力，此轴向力会导致管柱被拉断、封隔器失封等问题[3]，为准确计算管柱因温度变化的伸缩量，进而计算出附加轴向力，合理控制油套管平衡压力，保障压裂、酸化时管柱安全，需针对深井、超深井注入过程井筒温度场模型进行分析研究。

20 世纪60 年代开始，RAMEY[4]首次提出了井筒传热的简化模型，该模型假设井筒内为稳态传热，地层为非稳态传热，认为流体温度为井深和时间的函数，并引入井筒总传热系数和无因次传热函数来简化井筒传热过程，较好的解决了注入井井筒传热问题。在此之后，部分学者修正了无因次时间函数[5]，引入松弛距离和热储存系数到井筒传热方程[6]，极大地简化了计算过程；部分学者研究了流体摩擦热[7]、注入和产出过程[8]、深水钻井过程[9]、多因素耦合过程[10]、CO2埋存过程[11]、储气库注采过程[12]、井筒蜡沉积现象[13]、超临界CO2压裂过程[14]以及井筒达到稳定温度的时间[15]对井筒温度分布的影响，极大地丰富了井筒温度场模型的应用范围。但目前主要研究的数值模型其精度受计算步长的限制，在对深井、超深井计算时，小步长会显著增加计算时间与成本，解析模型精度不受计算步长影响。此外，现有模型大都假设井筒为均匀垂直管柱或简化的井筒模型，没有考虑深井、超深井复杂井身结构对井筒换热的影响。

本文在现有模型研究的基础上，考虑深井、超深井井身结构特点及地层传热机理，建立了深井、超深井注入过程井筒温度解析模型并推导出解析解。以某超深井实际数据为基础，探究复杂井身结构及地层温度计算方法对井筒温度的影响，实现准确预测超深井注入过程全井段温度，以期为后续管柱力学分析提供数据支撑；分析注入流体温度和注入排量对井底温度分布的影响，以期为压裂方案参数优化提供理论依据。

1 井筒温度场模型的建立

1.1 模型基本假设

油气井真实井身结构一般包含表层套管、技术套管、油层套管，套管外还有水泥环和环空，酸化、压裂等注液过程中，热量在地层-井筒各区域内热量交换方式复杂，为了更简便和精确地预测井筒温度场，以垂直井为例，做如下假设：

（1）流体不可压缩，注液前井筒已与地层达到热平衡，流体注入速率恒定；（2）流体不发生相变，忽略比热容、密度等参数随温度的变化；（3）忽略井筒和地层沿井深方向上的热交换，忽略热辐射；（4）地层温度线性变化，考虑井口温度不恒定，假设井口温度等于恒温层温度，也等于当地年均气温；（5）油管、套管、水泥环为同心圆结构。

1.2 井筒温度场模型控制方程

以井口为坐标原点，流体流动方向为正方向，在油管上取一长为dz 的微段，根据能量守恒定律和热力学定律在该微元段建立平衡方程：

式（1）两边同除以dtdz 并对t 和z 取极限，可得微分方程形式：

式中：m-单位深度流体质量，kg/m；m'-单位深度井筒系统质量，kg/m；E-流体内能，J/kg；E'-井筒系统内能，J/kg；t-时间，s；z-深度，m；w-流体质量流量，kg/s；H-流体的焓，J/kg；v-流体流速，m/s；g-重力加速度，m/s2；Q-单位长度地层向流体传入的热流量，W/m。

式（2）右边第一项表示单位长度流体内能变化率，第二项表示单位长度井筒介质（油套管、水泥环）内能变化率并且引入热储存系数来表征两者之间的关系，即m'E'=CTmE。热储存系数反映的是井筒储存或释放热量的能力，为流体质量和流体热容的倍数，通常在开井时取3，关井时取2。因此，式（2）右边前两项可以改写为：

式中：Cpf-流体定压比热容，J/（kg·°C）；Tf-流体温度，°C。

式（2）右边第三项表示单元体流入或流出的能量，假设质量流量w 不随深度z 发生变化并将基本热力学公式dH=CpfdTf-CpfJdp 代入可得：

式（2）左边第一项Q 为地层损失的热量，可以表示为：

式中：Tei-对应深度的地层温度，°C；Tf-地表温度，°C；LR-松弛距离参数，m-1；Uto-井筒总传热系数，W/（m2·°C）；ke-地层导热系数，W/（m·°C）；TD-Hasan推荐的无因次时间函数；tD-无因次时间，，α 为地层热扩散系数，m2/s。

将式（3）～（5）代入到式（2），并用集总参数Φ 来表示焦耳汤普森系数和动能的影响，即可得到流体温度随时间和深度变化的线性微分方程：

1.3 井筒温度场模型控制方程求解

由式（8）可知，Tf为时间t 和井深z 的函数，为求解此方程，先假设其为稳态，消除时间项后得到关于井深的一阶线性常微分方程：

求解式（9）得到稳态温度场模型，可知温度梯度表达式为：

现有传热模型都假设入口处流体温度等于地表温度，而实际情况两者存在温差，引入ΔT=Tf-Tinj来修正模型。将式（10）代入式（8）中消除温度梯度项，得到关于时间的一阶线性常微分方程：

为简化式（11），引入系数a 和b 来代表式（11）某些复杂项并进行求解，可得注入过程井筒瞬态传热方程的解：

由式（13）可知，井筒温度由右侧第一项地层温度和第二项a、b 和LR等参数组成的复杂项两者共同决定。在计算地层温度Tei时，不同计算方法（从井口向井底计算与从井底向井口计算）存在误差；右边第二项复杂井身结构导致每一段的热物性参数都不同，这同样对井筒温度的计算结果产生影响。

2 模型验证与数据对比

2.1 算例井基础参数

为验证本模型的准确性，以现场某井实际数据进行模拟计算与分析，实现注入过程井筒温度的预测。算例井完钻井深8 866 m，地表年平均温度15.00 ℃，注入液温度20.00 ℃，原始井底温度200.00 ℃，注液排量2 m3/min，注液规模410 m3，实测酸压后井底温度为80.00 ℃，具体井身数据见表1。

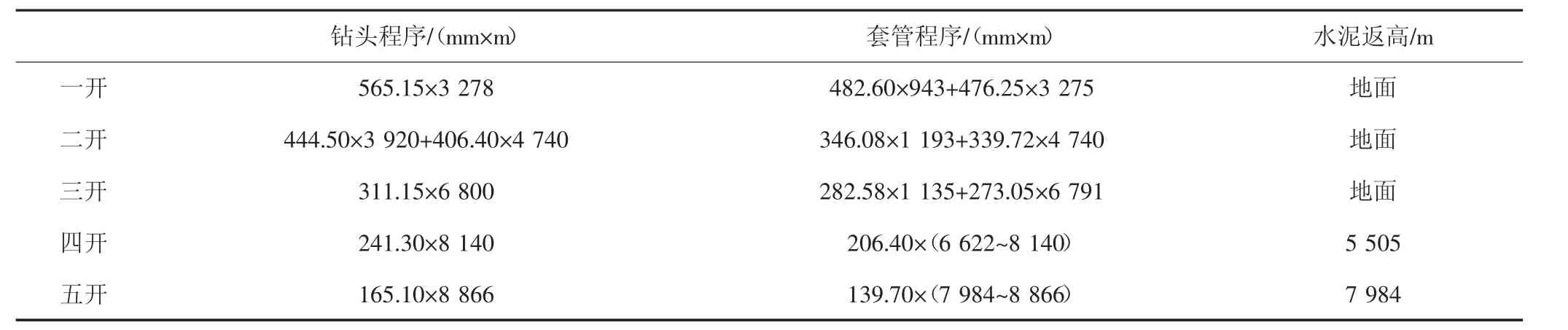
表1 算例井井身数据

2.2 复杂井身结构对井筒温度的影响

为探究复杂井身结构对井筒传热的影响，采用同种数据结构和计算方法，分别计算考虑复杂井身结构和不考虑复杂井身结构的井筒温度分布。考虑油套管内外径、水泥环及环空尺寸位置变化，对上述井例进行温度计算时将井筒分为多段并分别计算传热参数；不考虑复杂井身结构时，假设油管尺寸不变且认为油层套管外水泥环直接与地层接触。计算结果见图1 左图。

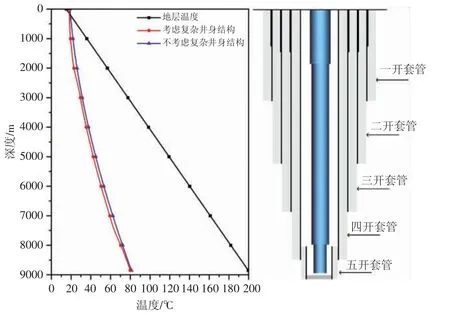
图1 复杂井身结构对井筒温度的影响

由图1 左图可知，考虑复杂井身结构时计算的井底温度为79.55 ℃，与实测值相差-0.45 ℃，绝对误差-0.56%；不考虑复杂井身结构时计算的井底温度为81.22 ℃，与实测值相差1.22 ℃，绝对误差1.52%。上述数据表明，考虑复杂井身结构时井筒温度场模型精度更高。

考虑复杂井身结构时，从井口至井底水泥环的半径逐渐减小，而水泥环的导热系数比地层的导热系数小，这意味着热量在井筒和地层之间传递的更慢，因此，考虑复杂井身结构计算的井筒温度略低于不考虑复杂井身结构时的井筒温度。对比右侧井身结构示意图可知，井身结构发生变化时，对应井深处的温度曲线也会发生波动。出现该现象的原因是井身结构的变化导致井筒流速、总传热系数和松弛距离等参数发生变化，对该位置温度计算结果产生影响。

2.3 地层温度计算方法对井筒温度的影响

地层温度的精确计算会对井筒温度分布有重要影响。已知井口温度向井底计算地层温度时，井口温度易受环境影响，需采用恒温层温度替代，并且恒温层温度近似等于当地平均气温；已知井底温度向井口计算地层温度，需已知井底温度。采用以上两种计算方法分别对井筒温度进行计算并对比，结果见图2。

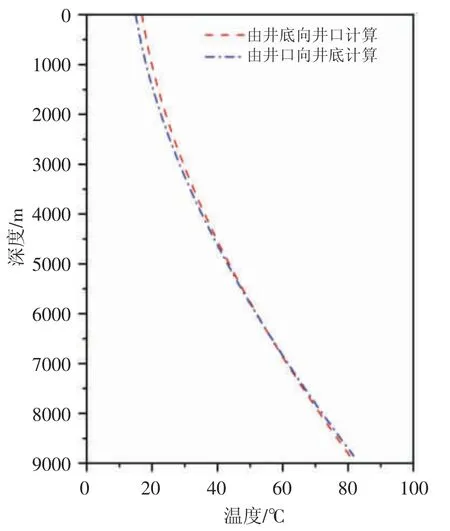
图2 地层温度计算方法对井筒温度的影响

由图2 可以看出，井口和井底处温度差值较大，井口处相差1.91 ℃，井底处相差1.16 ℃，井筒中下段两曲线结果趋于一致。导致该结果的主要原因是：井口或井底处温度值来源不同。井口温度前者由当地平均气温代替，后者由井底计算得到；井底温度前者由井口计算而来，后者井底温度为已知值，数据本身存在误差。但两方法计算的井底温度结果相差不大，均已满足现场需求，井底温度已知时，建议采用井底向井口计算井筒温度。

3 影响参数分析

3.1 注入流体温度对井底温度的影响

注入流体温度不同，井筒与地层的换热量也不同，固定注入排量2 m3/min，通过改变注入流体温度对井筒温度场进行模拟，酸压施工时间为3.5 h，注入流体温度分别为10.00、20.00、30.00 ℃时，计算结果见图3，酸压结束后井底温度分别降低至76.78、79.55、85.17 ℃。

图3 不同注入流体温度下井底温度随时间变化曲线

由图3 可知，降低注入流体温度可以有效降低井底温度，温度每降低10.00 ℃，井底温度约降低4.20 ℃。注入流体温度越高，井筒内流体与地层温差越小，换热效率越低，井筒与地层换热量也就越少。因此，可在适当的范围内选择注入流体温度来降低井底温度。

3.2 注入排量对井底温度的影响

注入排量的增加会明显加快注入流体到达井底的速度，流速的变化也会影响对流传热效率。固定注入流体温度为20.00 ℃，计算施工排量为1、3、5 m3/min 时的温度变化情况，结果见图4，酸压结束后井底温度分别降低至108.81、73.98、58.18 ℃。

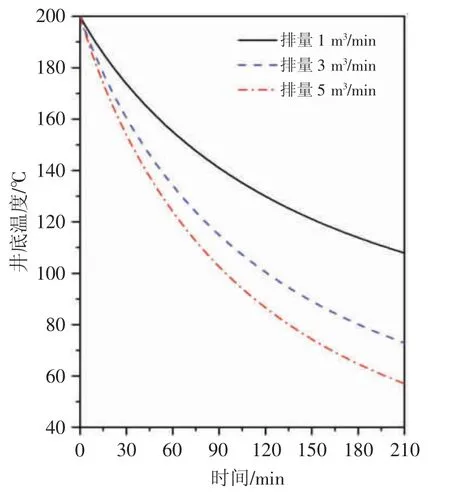
图4 不同排量下井底温度随时间变化曲线

由图4 可知，增加排量可以有效降低井底温度。排量越高，温度降低速度越快，这是因为排量增大后对流传热效率增加，换热速度加快。随着排量的增加，井底温度变化量逐渐减小，说明排量对井底温度的影响并非线性的。因此，针对深井、超深井注入过程，可在合理的范围内选择注入排量来控制流体温度，持续增加排量来降低井筒温度，成本较高且效果可能并不明显。