例谈模型意识的培养策略

倪艳

《义务教育数学课程标准（2022年版）》指出，模型意识是伴随小学数学学习的核心素养之一。笔者以“相遇问题”的教学为例，谈谈如何在数学教学中培养学生的模型意识。

一、原型转化，初步感知模型

“相遇问题”属于“行程问题”，是较难理解的数学问题，学生需要具备一定的抽象思维能力才能解决这类问题。教师可以使用具体、形象的方式演示抽象的“相遇问题”，唤醒学生已有的生活经验，让学生初步建立“相遇问题”的模型。

课堂上，教师首先引导学生玩“纸飞机”的游戏，让学生在游戏中感知速度、时间、路程、方向几个要素及它们之间的关系。接着，教师选择两名学生演示“相遇问题”的场景。模拟情境时，当学生喊出口令“预备——开始”，两名学生面对面从相对的方向出发，直到相遇后停下。有的学生发现相遇时速度快的同学走的路程长一些，速度慢的同学走的路程短一些；有的学生发现他们同时出发，同时停止运动，用时相同；有的学生发现相向而行是两人从相对的方向面对面出发；还有的学生发现他们走的总路程是一名同学走的路程与另一名同学走的路程之和。在此基础上，教师让两名学生演示相向而行但尚未相遇的情况，即喊停时两人之间还有一段距离，学生感知到在这种情况下，一名同学走的路程加另一名同学走的路程，再加未走完的路程，等于总路程。教师采用让学生演示的方式化静态知识为动态体验，让学生直观感知“相遇问题”的数学模型，轻松悟出了“相遇问题”中的要素及其基本数量关系。

二、多元体悟，经历建模过程

解决“行程问题”的前提是学生经历建模过程，多元体悟并建立模型。教师要启发学生学会审题并提取关键信息，分析题目中的数量关系，辨析题目中的变量，建构“相遇问题”的模型并应用模型。

课堂上，教师出示例题：“小米和小花分别从各自的家同时出发，相向而行。小米的速度为40米/分，小花的速度为60米/分，5分钟后两人相遇。小米家和小花家相距多少米？”教师先提示学生审题时要抓住“题眼”，提取关键的四个要素：两地、同时、相向、相遇。接着，教师启发学生从具体到抽象地展开思考，并运用数形结合的数学思想方法画出线段图（如图1），表示出运动的要素：运动地点、速度、时间、方向、距离等。这样做，题目中的条件和问题一目了然，有利于学生分析、提炼题目中数量关系的模型。通过以上学习过程，学生明晰了“相遇问题”的数量关系，比较容易地发现了解题思路：可以先求小米5分钟走了200米，再求小花5分钟走了300米，最后求出总路程500米，进而提炼出“路程部分量+路程部分量=路程总量”的数量关系模型。

实际教学中，部分教师会在学生掌握第一种解题方法的基础上，直接引导学生运用乘法分配律得出第二种解题方法，并让学生机械记忆相应的第二种思路：运用“速度和×时间=路程”的模型解题。然而，这种转化方式很难让学生真正理解这一模型。为此，教师可以通过画线段图法帮助学生抽象出该模型。学生发现：小米和小花第1分钟共同走了“40+60”米，第2分钟又共同走了“40+60”米，进而提炼出两人每分钟行“40+60”米，相遇时共走了5个“40+60”米。学生讨论发现，第二种思路仍是“速度×时间=路程”的数量关系模型，并体会到画线段图有助于更直观、深刻地理解“相遇问题”中的等量关系。

三、整体贯通，体会模型价值

在模型的应用阶段，教师要联系生活实际设计分层练习，帮助学生在解决“相遇问题”的过程中更好地理解问题的本质和解题策略，从而提高学生的高阶思维能力，使他们形成结构化的数学思维。

应用模型环节，教师可以让学生逐层体会模型的价值。基础题采用让学生自主分类编题的形式，要求学生用数学语言表达不同类型问题的数量关系、解决方法及注意要点。学生类比例题列举出生活中相向开车、相向游泳、相向跑步等常见的“相遇问题”。在学生理解并掌握“相遇问题”数学模型后，教师通过引入《九章算术》中的数学名题“今有凫（野鸭）起南海，七日至北海；雁起北海，九日至南海。今凫雁俱起，问何日相逢？”，让学生在感受中华优秀传统文化的同时，进一步建构“相遇问题”模型。

在理解并解决此问题的基础上，教师通过出示情境不同但本质相同的购物问题、打字问题、合修公路等同质问题，不断丰富模型。通过模型的演变与关联，学生整体建构了乘法数量关系的模型，剥离不同情境的“外壳”后，认识到这些问题都属于同类问题，其数学模型的实质都是“每份数×份数=总份数”，真正达到了融会贯通。这样教学，拓展了学生模型意识建构的宽度和深度，促进了学生数学知识的理解和迁移。

学生掌握基础题组后，教师可以采用先扶后放的方式，适当给出提高型变式问题，增加问题解决的思维含量。如在出示“甲、乙两车同时从相距290千米的两个地点相向而行，甲车的速度是每小时60千米，乙车的速度是每小时40千米，多少小时后两车相距110千米？”的问题后，教师巧妙地变化运动情境：“若两车相遇后继续前行，多少小时后又相距110千米？”“如果两车不是同时出发的，有一辆车先出发，怎样求相遇时间？”学生的兴趣高涨，在教师的引导下，通过独立分析、小组交流解决了上述问题。以上教学，通过行程中要素的不同组合方式，演变出千变万化的运动状态，使学生的模型意识得以深度构建，达到了一通百通地应用模型的学习效果。

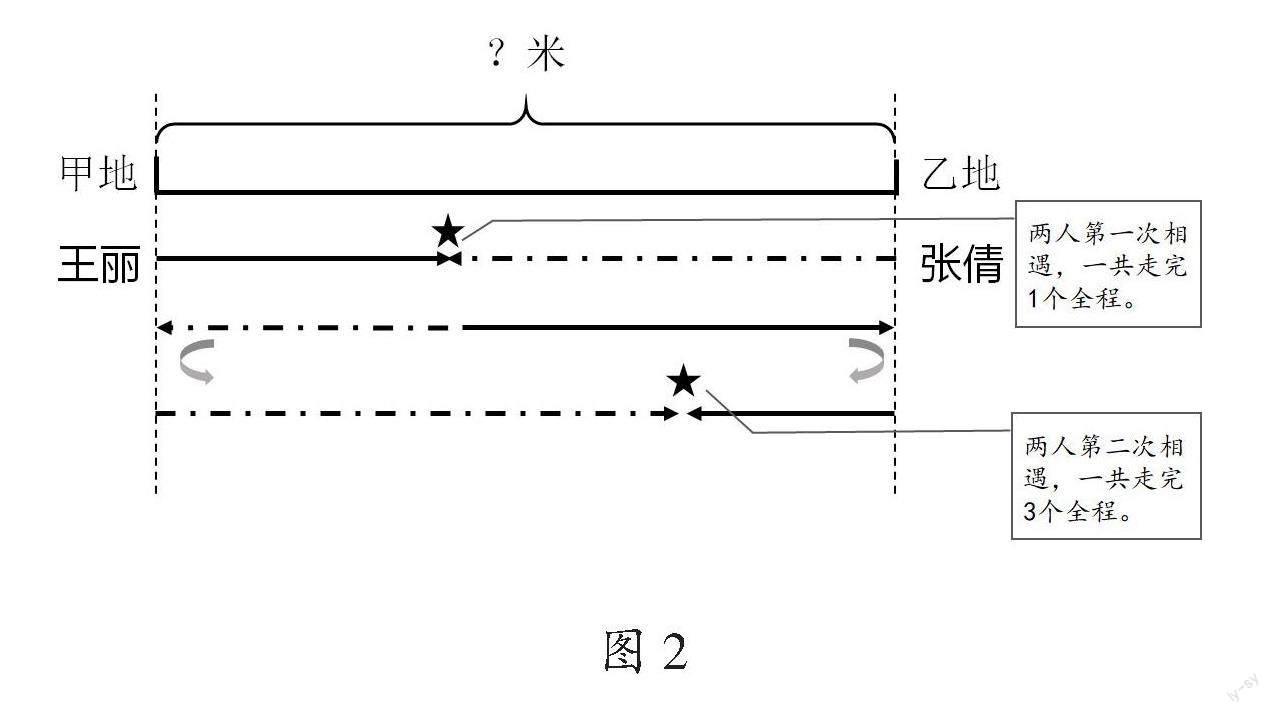
随后，教师出示复杂情况下的拓展题，利用学生的易错点强化学生的模型意识。如“王丽和张倩分别从甲、乙两地同时出发，王丽每分钟走60米，张倩每分钟走75米，经过7分钟两人第二次相遇。甲、乙两地相距多少米？”学生出现了两类看法，一类学生认为第二次相遇就是共走了2个全程，1个全程应该用“（60+75）×7÷2”来表示；另一类学生提出了反对意见，他们用线段图表示出两人的行程情况（如图2）。学生豁然开朗，并达成了共识——两人第二次相遇其实一共走了3个全程，体会到解决复杂行程问题最直接有效的方法是画线段图表示题中的信息，利用抽象出的几何模型化繁为简，帮助我们分析问题。

学生从“望题生畏”到豁然开朗的过程中，运用数形结合的方法直观理解了行程中的关键信息及其关系，发现了“数学模型”是巧解复杂行程问题的脚手架，深度体验到数学思维的乐趣，感悟到数学模型的价值。

此外，教师还可以利用思维导图或数学日记引导学生回顾、整理“相遇問题”的不同类型，分析其异同及解决问题的注意要点，反思、交流在建模过程中的困惑及解决方法，如此拓展深化模型，帮助学生形成稳固且变通的模型，发展数学核心素养。

（作者单位：江苏省泰州市大浦中心小学）

责任编辑  张敏