一种融合GA和LSTM的边坡变形预测优化网络模型及其应用

肖海平 王顺辉 陈兰兰 范永超 万俊辉

1 江西理工大学土木与测绘工程学院,江西省赣州市客家大道1958号,341000

2 江西理工大学应用科学学院,江西省赣州市客家大道156号,341000

随着工程建设的不断发展,出现越来越多的高陡边坡,在地质、降雨、人工扰动等内外因素的影响下,边坡变形、失稳以及滑坡等事故频发,造成重大的财产损失和人员伤亡。为保证边坡安全,准确分析其稳定性及变化趋势,开展边坡变形预测是边坡灾害预防和控制的重要研究内容。

目前,国内外学者就边坡变形预测进行大量研究,取得一定成绩,实现了从简单到复杂、从单一到组合、从线性到非线性模型的发展。盛建龙等[1]运用GM(1,1)模型对老鹰嘴边坡位移进行预测分析;杨振兴等[2]利用回归分析和小波变换分解边坡变形数据的趋势项和误差项;陈兰兰等[3]通过GA-BP网络模型对越堡水泥矿山边坡监测数据进行分析预测,得出该模型在边坡变形预测方面具有一定的可靠性和可行性;Sun等[4]提出一种新的机器学习方法,对安家岭露天矿进行分析表明,所建立的边坡变形模型能够较准确地预测被监测矿山的边坡变形;刘小生等[5]通过GA-SVR模型基于边坡变形监测数据进行预测和分析,得出其预测结果接近真实值;Xi等[6]对基于监测时间序列位移数据的边坡变形预测的机器学习方法进行比较研究,得出Transformer模型更适合于预测受多种因素影响的非线性滑坡位移。以上模型各有优势,但也存在一定的不足:灰色预测模型在短期预测中具有较好的精度,但在长期预测中预测精度会受到影响;回归模型的精度依赖于建模因子的选择;BP神经网络模型没有考虑到边坡监测数据的时间相关性;组合模型也存在通用性较差的问题,容易陷入局部最优解,导致精度不高。

本文考虑到BP神经网络模型忽略边坡监测数据存在的时间相关性,以及LSTM模型由于超参数选择存在主观性而导致陷入局部最优等问题,提出遗传算法-长短期记忆(genetic algorithm-long short term memory,GA-LSTM)预测模型,充分发挥遗传算法全局搜索能力和LSTM预测时序数据的优势,以提高边坡变形预测的可行性及准确性。

1 算法模型基本原理

1.1 LSTM神经网络

LSTM神经网络是一种特殊的循环神经网络(recurrent neural network,RNN)[7]。由于RNN的内部单元可以通过时间间隔进行连接,因此适用于处理序列数据。LSTM网络采用门设计,避开了梯度爆炸和长期依赖问题[8]。因为有一组门控单元来控制信息的流动,它可以处理输入之间随时间发生变化的长期依赖性(图1)。LSTM节点包含4个部分:

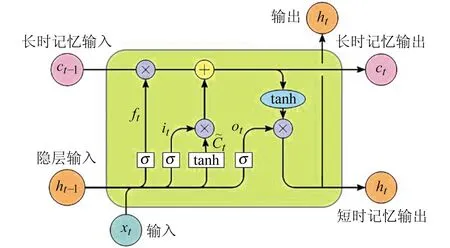
图1 LSTM神经单元Fig.1 Neural unit of LSTM

1)遗忘门:用来控制信息的保留程度。遗忘门会计算一个[0,1]之间的数值,数值的大小表示细胞状态中忘记多少信息、保留多少信息[9]。如果门值为0,则表示全部遗忘;如果门为1,则全部保留。遗忘门计算公式为:

ft=σ(Wf[ht-1,xt]+bf)

(1)

式中,σ为sigmoid激活函数,Wf为对应遗忘门的权重系数(下标表示遗忘门),bf为相应的偏置项,ft表示遗忘门输出结果,t表示神经单元所处的时间步。

2)输入门:用来控制哪些信息应该被输入到细胞状态[10]。输入门根据当前输入向量xt和上一个时刻的隐藏状态计算一个[0,1]之间的数值,该数值表示当前输入的重要程度,再将重要程度较高的信息加入到细胞状态中。输入门计算公式为:

it=σ(Wi[ht-1,xt]+bi)

(2)

(3)

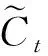
3)细胞状态:在LSTM中,细胞状态就是网络所保留的长期记忆。长期记忆计算公式为:

(4)

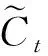
4)输出门:用于控制当前时刻细胞内部的状态并决定有多少信息输出给下一个LSTM细胞[11],计算得到当前时刻的隐藏状态ht。输出门计算公式为:

ot=σ(Wo[ht-1,xt]+bo)

(5)

ht=ot*tanh(Ct)

(6)

式中,ot表示t时间步下输出门输出的结果。式(6)中Ct表示时间步为t时的长时记忆输入,经tanh激活函数后与ot相乘得到短时记忆输出ht。

1.2 遗传算法优化LSTM模型

遗传算法(GA)是一种全局搜索算法,能较好地解决参数优化问题。在LSTM模型的参数优化方面,主要是用来优化LSTM模型的超参数组合,比如时间步大小、神经网络隐藏层层数、每层LSTM神经元个数以及优化器种类等。建立备选超参数库,经过GA算法得到最优的超参数组合,用最优超参数组合建立最终模型。具体步骤如下:

1)确定参数空间:待优化的LSTM模型参数的空间,主要包括每层LSTM的units数、隐藏单元数、激活函数种类以及优化器种类等。参数空间的确定需要根据具体问题,保证足够客观[12]。本次实验所选参数空间如表1所示,其中时间步为时间位移及模型输入,隐藏单元数为中间隐藏层LSTM单元个数。

表1 参数空间

2)初始化种群:在确定参数空间后,需要对种群进行初始化操作。在遗传算法中种群是指问题可行解的集合。在初始化种群时,不但要避免组合的重复性,还要注意初始化的随机性。

3)计算适应度:在种群经过随机初始化后,依据定义好的适应值函数计算个体的适应度。适应度是指个体适应环境的能力,也就是在解决该问题上效果更优。对于LSTM模型,使用交叉验证的方法来计算每个个体的适应度。

4)选择优秀个体:依据个体的适应度值的大小来选择优秀个体,对优秀个体进行繁殖。

5)交叉繁殖:选择优秀个体的后代,进行交叉繁殖操作。可以使用单点、多点或均匀交叉繁殖等方法进行LSTM模型的参数优化。

6)变异操作:完成交叉繁殖后,需对新生成的个体进行变异操作。在LSTM模型的参数优化中,可以使用插入、删除或替换等变异操作。

7)重复迭代:完成上述步骤后,需重复迭代上述交叉变异繁殖等步骤,在每一次迭代中不断优化超参数组合,直到达到预定的停止条件为止,比如设置好迭代次数、适应度大小或达到最优解等[13]。

2 实例分析

2.1 工程概况

选取海明矿业露天边坡为研究对象,在其北侧边坡稳定区域布设GNSS基准站1套,东边坡布设GNSS监测站6套,用于监测边坡表面位移变化量。本次实验所使用的地表位移监测设备为高精度GNSS专用接收机P5,其水平静态精度为±2.5 mm+0.5×10-6(RMS),垂直静态精度为±5 mm+0.5×10-6(RMS)。各GNSS监测设备的响应时间为1 h一次,最快为每组1 min。本次实验以GNSS49点为例,采用10 min获取1组数据的方式,数据集的时间跨度为2023-03-01～2023-03-15,共得到2 000条监测数据。图2为监测点GNSS49在边坡的具体位置,图3(a)为GNSS49点的X、Y、Z累积位移2D展示图。由于数据量较大,在图3(b)中只选取时序(指采集数据对应的时序)为0、500、1 000、1 500、2 000对应点坐标进行位移3D展示,其中dX正方向为正北方向(N),dY正方向为正东方向(E),dZ方向满足右手定则,在图中记作H。考虑到监测数据量大、版面有限,表2仅列出监测点GNSS49的部分监测数据。

表2 监测点GNSS49部分监测数据

图2 GNSS49点位分布Fig.2 Distribution of GNSS49 point

图3 GNSS49监测点位移监测原始数据变化Fig.3 Changes in raw data for displacement monitoring at GNSS49 monitoring point

2.2 GA-LSTM优化网络模型的应用

通过GA算法对LSTM模型超参数进行选择,找到全局最优解。依据最优超参数组合构建预测模型,将监测数据前80%作为训练数据集,后20%作为测试集,用划分好的训练集对模型进行训练,训练好模型后对测试集进行预测,并记录模型的损失值(loss),用均方误差(mean square error,MSE)表示。模型预测结果图(图4～6)包含监测点的X、Y、Z累积位移变化量预测,在各模型的predict_result图中横轴表示采集数据对应的时序,纵轴表示累积位移量。图中原始累积位移数据为蓝色曲线,预测结果分为训练数据集(橙色曲线)和测试数据集(绿色曲线)。

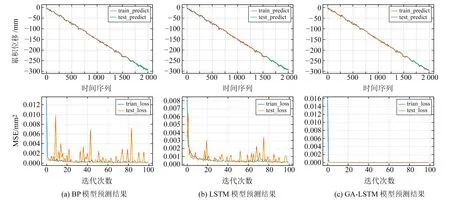
图4 GNSS49-X方向不同模型预测值Fig.4 Prediction values of different models in GNSS49-X direction

图5 GNSS49-Y方向不同模型预测值Fig.5 Predicted values of different models in GNSS49-Y direction

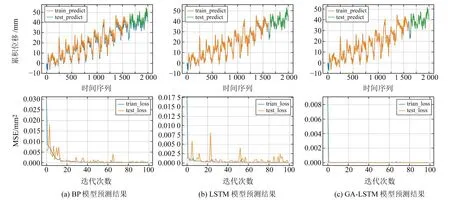
图6 GNSS49-Z方向不同模型预测值Fig.6 Predicted values of different models in GNSS49-Z direction

本次实验各模型的loss_result图中,模型训练一共需要迭代100次,其中横坐标epochs表示迭代次数,纵轴表示每次迭代后计算的MSE。程序会记录下每次迭代后训练数据集的MSE损失,以及测试数据集的MSE损失,蓝色曲线表示训练数据集的MSE损失值的变化情况,橙色曲线表示测试数据集的MSE损失值的变化情况。

在GA算法优化超参数时,个体的适应度值通过计算测试集的均方根误差(root mean square error,RMSE)获得。RMSE也作为模型精度评价指标,RMSE值越小,表明预测位移值与真实位移值之间的误差越小,预测结果越准确。其中RMSE的单位为mm,从RMSE的大小可以直观地看出模型的整体误差大小,从而确定模型对应的精度情况。

根据不同的模型研究方法,可以得到图4～6不同模型边坡变形监测预测结果及loss_result图,表3～5中包含03-13、14、15监测值(对应时序为1 709、1 853、1 997)与模型预测值对比情况以及模型迭代100次后训练集的RMSE值和测试集的RMSE值,并在相同的计算设备上比较各模型RMSE损失值小于1 mm时模型训练的时间。

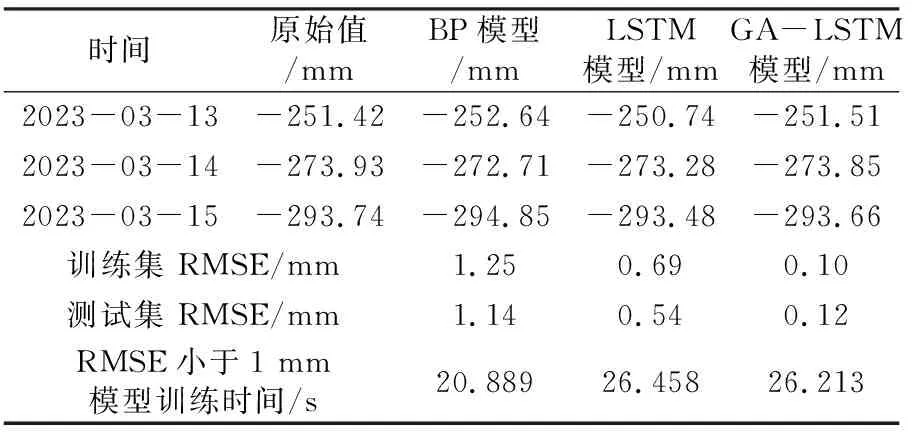
表3 GNSS49-X方向不同模型预测值对比

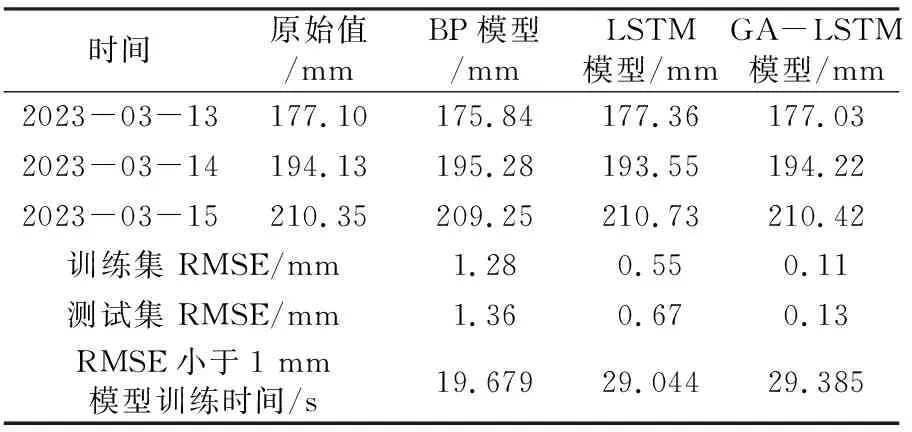
表4 不同模型预测GNSS49-Y对比

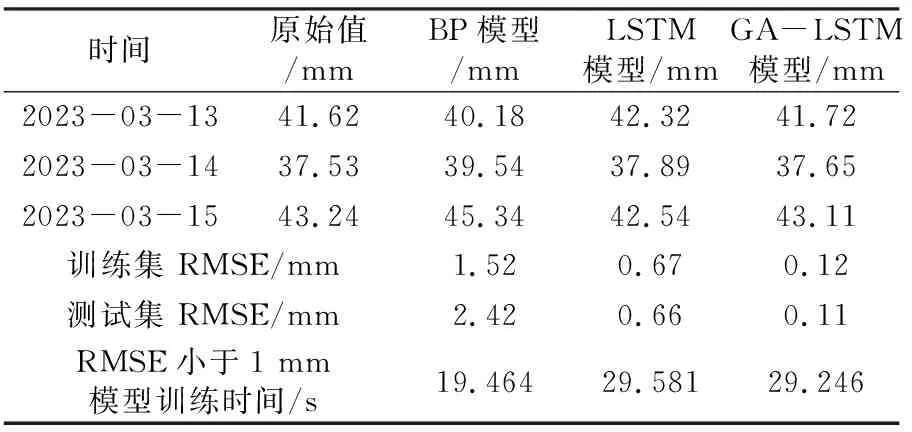
表5 不同模型预测GNSS49-Z对比

图4～6以及表3～5的研究成果表明:

1)BP神经网络模型的预测结果误差RMSE在1～3 mm,最高为2.42 mm,模型整体精度不如LSTM和GA-LSTM两个模型,模型损失达到收敛需要更多的迭代次数,预测误差不稳定,容易陷入局部最优解,没有考虑到监测数据的时间特性。但在相同的收敛条件下,3个模型训练时间相差不大,BP神经网络模型耗时较少。

2)LSTM模型的预测结果误差比BP神经网络预测要好,为0.5～1 mm。但由于在超参数选择方面存在着主观性,无法找到真正适合实际应用的最佳超参数组合。测试误差相对稳定,整体不如GA-LSTM模型的预测结果。

3)GA-LSTM模型的整体预测误差较小,在0.2 mm以下,精度高并且模型损失达到收敛只需较少的迭代次数,整体MSE损失值波动较小,模型稳定性较好,具有较好的拟合效果。

4)本文分别采用3种预测模型对变形监测点2023-03-13、14、15的变化量进行预测,实验结果表明,GA-LSTM模型预测值与实际变形原始值拟合较好,能较好地预测监测点位移变化情况。

3 结 语

本文在采用不同模型分析其MSE损失值的变化及其RMSE数值的基础上,以海明矿业露天采场边坡为研究对象,对监测点GNSS49进行预测分析,得出以下结论:

1)本文提出的GA-LSTM优化模型,解决了BP神经网络模型没有考虑边坡监测数据时序性以及LSTM模型超参数选择存在主观性而导致陷入局部最优等问题,其达到损失收敛的速度及稳定性有较大提高。

2)GA-LSTM模型预拟合准确性在0.1～0.2 mm,是LSTM神经网络模型的5～7倍,是BP神经网络模型的10～20倍。GA-LSTM模型具有较高的精度和稳定性,其预测值更接近于真实值。

3)考虑到模型运行效率,本次实验选择监测数据的时间跨度较小,未能全面反映边坡的整体变化趋势。为有效指导矿山边坡的安全生产和管理,应充分利用实际监测数据实现全域时间内边坡变形的预测,以分析其稳定性状态。