三支概念背景下属性粒化效率的度量*

2024-04-23张晓燕王佳一

计算机工程与科学 2024年4期

张晓燕,王佳一

(西南大学人工智能学院,重庆 400715)

1 引言

形式概念分析[1]是一种以形式背景为研究对象的理论,是一种以概念格相关理论为核心概念的数学工具,常用于进行数据分析。概念格展示了概念之间的偏序关系,刻画对象和属性的内在关系[2]。然而,基本的概念格因其只研究了“共同(被)具有”关系的问题,忽略了“共同不(被)具有”关系的问题而存在局限性[3,4],且这种局限性也导致该理论在实际应用中受到限制[5]。

2014年,Qi[6]提出了新的理论以弥补经典概念格理论的局限性,即三支概念分析。三支概念分析提出了对象诱导的三支概念格与属性诱导的三支概念格,2种三支概念格均同时研究了“共同(被)具有”和“共同不(被)具有”的问题。其所获得的三支概念格相较于以往经典概念格研究范围更加全面,也会使概念识别在实际应用过程中更加精确。

在三支概念正式提出后,许多学者对此进行了扩展和深入研究。Qian等[7]利用形式背景的叠置与并置,提出了三支概念格的构造方法,仿照对象诱导概念格与属性诱导概念格提出了对象诱导的三支面向对象概念格和属性诱导的三支面向属性概念格的定义,并分析4种概念之间的异同。苏新等[8]进行了基于对象和基于属性的三支概念格合并方法比较。Wei等[9]立足于三支概念格,在三支协调的意义下研究了决策背景的规则获取问题,并与强协调决策背景所获得的一般决策规则进行了详细的比较研究。

除对三支概念本身的扩展和推广,学科交叉融合研究也为丰富三支概念体系做出了极大的贡献。Li等[10]将多粒度与三支概念融合,提出了基于多粒度的三支认知概念学习。龙柄翰等[11]提出模糊三支概念分析,将模糊集理论与三支概念分析相结合,考虑模糊背景中“共同具有的程度”与“共同不具有的程度”2方面不确定的共性信息极大地提高了三支概念在生产力方面的意义。

多粒度研究方面,知识粒化[12]、属性粒化[13,14]和属性聚类[15]等概念的提出将多粒度与概念认知联系起来[16],为了缓解庞大的概念个数,在约束宽松的情况下减少工作量提供了解决方案,并且为获取数据的多层次概念知识表示与处理方法上提供了新的方法。多粒度方面的研究包括研究对象的粗化与细化,在属性粒化研究中,其主要研究方向包括属性的吸收,即粗化,以及属性的分解,即细化。在属性的粗化与细化之中,概念也会随之转化,可以获得在不同粒度上的概念分析。Belohlavek等[17]提出了给予属性粒化的形式概念分析方法,该理论中进行了属性粒化,生成不同粒度层次的形式背景的工具主要是粒度树与剪枝。

在三支概念格背景下,对属性粒化的研究尚且不足,且现在无法通过有效手段度量属性粒化效率,严重降低了概念区分与细化的速度,需要大量冗余的计算[18]。针对此种情况,本文提出以三支概念格为背景的属性粒化效率度量方法,尝试探讨对解决此类问题的方法。

2 基础知识

2.1 概念格

设有形式背景K=(G,M,I),其中,G为对象集,M为属性集,I为G和M之间的二元关系。在经典形式背景中,I的取值只有0或者1这2种可能。对于x∈G,m∈M,当I(x,m)=1时,表示对象x和属性m存在关系I;当I(x,m)=0时,表示对象x和属性m不存在关系I。

为研究对象子集和属性子集之间的关系,对于X⊆G,A⊆M,现定义如下2个分别作用于属性子集和对象子集的导出算子X*和A*:

X*={m:m∈M,∀x∈X,I(x,m)=1}

A*={x:x∈G,∀m∈A,I(x,m)=1}

特别地,当对象子集或属性子集中仅有一个元素时,记{x}*为x*,记{m}*为m*。

设有形式背景K=(G,M,I),若对于X⊆G,A⊆M,有X*=A且A*=X,则(X,A)称为一个形式概念,其中概念的外延为X,概念的内涵为A。形式背景K=(G,M,I)下的所有形式概念的集合为L(K),L(K)即为概念格[20]。

本节内容详见文献[2]中有关于概念格的理论叙述。

2.2 三支概念格

如果说概念格研究的是“共同具有”的关系,那么三支概念格就是同时研究“共同具有”和“共同不具有”2种关系。在应用中,只研究单方面往往会使研究结果具有片面性,从而在利用概念寻找对象和属性的过程中出现错误,而从正反2方面研究则会使研究结果更加精准,提高寻找结果的正确率。

为了研究“共同不具有”的关系,在这里定义2.1节导出算子的负算子。对于子集X⊆G,A⊆M,有:

显然,在负算子作用下,“共同不具有”这一关系可以被研究。但是,如果需要同时研究具有和不具有的关系,还需要定义一对算子。特别需要说明的一点是,单个对象子集在运算后会得到2个属性子集,即“共同具有的属性”和“共同不具有的属性”。同理,由于出发点不同,单个属性子集在运算后会得到2个对象子集,从而可以得出2种概念。

对于X⊆G和A,B⊆M:

若XO=(A,B)且(A,B)O=X,则(X,(A,B))为对象诱导的三支概念,简称OE概念,其中,X为OE概念的外延,(A,B)为OE概念的内涵。

对于X,Y⊆G和A⊆M:

若AA=(X,Y)且(X,Y)A=A,则((X,Y),A)为属性诱导的三支概念,简称AE概念,其中,(X,Y)为AE概念的外延,A为AE概念的内涵[21]。

本节内容详见文献[8]中有关三支概念格定义的叙述。

2.3 属性粒化

属性粒化是一种由旧的属性集构建新的属性集的方式,其构建方法是根据不同属性的内在联系,通过粒度树与剪枝的构造得到不同的属性集。相对于纯代数构造方法,通过粒度树这一工具的属性粒化显然要求属性之间存在某种关联,至少是人为规定的联系。

对于形式背景K=(G,M,I),任意属性m∈M,属性m的粒度树Tm是满足以下全部条件的含有根节点的树:

该树中的任意一个节点都代表一个属性,且都有确定且唯一的名称来标记。树的根节点为m。

对于每一个节点,此处记为z,均有一对象集合z*∈G,该对象集由具有属性z的集合构成。

剪枝C是粒度树Tm上满足如下条件的节点集:对于每一个叶节点u而言,在从u到根节点m的路径上存在唯一的节点存在于该剪枝。给定形式背景K=(G,M,I),如表1所示,其中,G={a,b,c,d,e}为对象集,M={Color, Black, Red, Blue, Light blue, Dark blue}为属性集,I为G和M之间的二元关系。

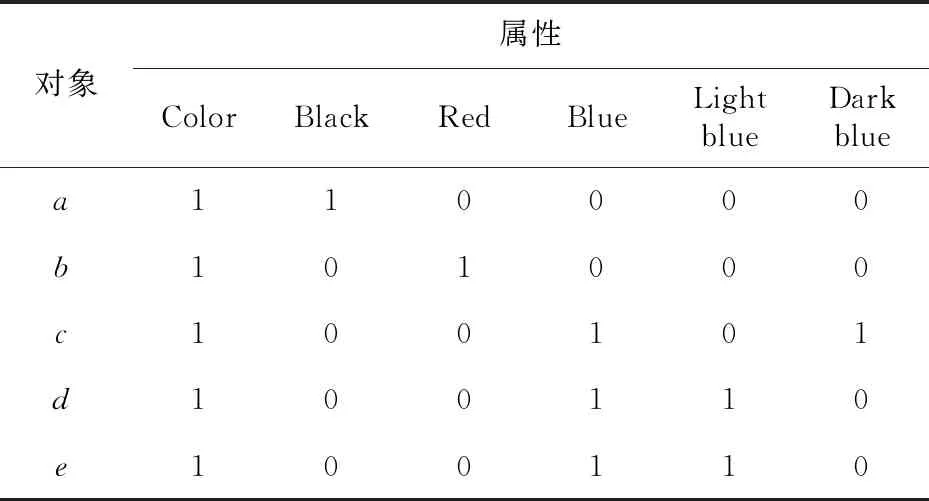
Table 1 Formal background K=(G,M,I)

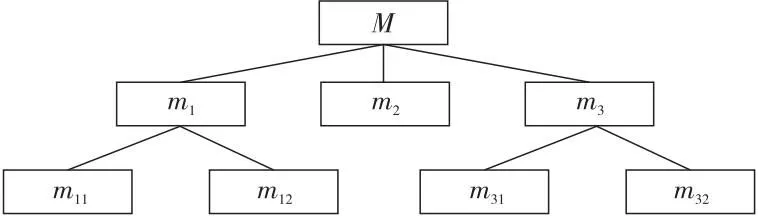
表1中基于属性集的粒度树如图1所示。

Figure 1 Granularity tree corresponding to attribute set in table 1

{Red,Light blue,Dark blue}不是剪枝,因为其到根节点Color的路径上还有Black这一子节点。{Blue,Red,Light blue,Dark blue}是剪枝。

对于X⊆G,A⊆MC,有:

X*C={m:m∈MC,∀x∈X,IC(x,m)=1}

A*C={x:x∈G,∀m∈A,IC(x,m)=1}

得到粒度树后,可以通过从粒度树上获取不同的剪枝得到不同的粒度层次,有些粒度层次之间存在偏序关系,而有些粒度层次之间不存在偏序关系。本文将对这2种情况分别进行讨论。

本节内容详见文献[15]中关于粒度树、剪枝及属性粒化的叙述。

2.4 获取概念格

引理1设K=(G,M,I)是一个形式背景,对于X,X0⊆G和A⊆M,下面性质成立:

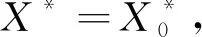
(2)若X*=A和X⊆A*,那么(A*,A)是一个概念。

引理1是Next Clousure算法的基础,利用此概念可以获得所有概念,所有的概念组成概念格L(K)。Next Clousure算法如算法1所示。

算法1 Next Clousure算法输入:形式背景K=(G,M,I)。输出:全部概念集合C。步骤1 初始化C=⌀;重命名全部对象为1:i;步骤2 令C=C∪{⌀**,⌀*};/*为对象子集和属性子集导出算子,**是*的二次运算,即复合运算*/D=sort(G,DESC);/*将对象集元素进行分类并按降序排序*/步骤3 S=⌀*; while S≠⌀**do J=D-S; foreach i in Jdo F=(S∩{1,…,i-1}∪{i})*; T=F*; U=T∩{1,…,i-1}; if i∈T-S and S∩{1,…,i-1}=U then C=C∪{T,F}; S=T; break; endif endfor endwhile步骤4 return C

利用Next Clousure算法同样可以得到反概念。反概念是相对概念而言的,反概念可以看作是原形式背景的补背景下的概念。对于一个形式背景,所有反概念组成该形式背景下的反概念格。

3 存在偏序关系的不同粒度层次

3.1 属性粒化前后三支概念

属性粒化前后,形式概念背景中的属性集也随之进行了粗细转化,在由粗属性集到细属性集的转化中,对于相同对象集,新属性可能部分出现在与之对应的属性集中,也有可能全部不出现在对应的属性集中。

现实应用中,属性粒化常用于更加精确地定义概念。例如,在将“不同种类牛仔裤”进行区分定义时,某属性可以由“蓝色”到“深蓝色”及“浅蓝色”,再到具体色号层层细化,使定义更加细化。而在属性粒化由粗到细的过程中,随着属性集向更细的方向转化,必定会有更多概念的形成。以下将对此结论进行理论证明。

为了方便说明,对于剪枝后的形式背景KC=(G,MC,IC)形成的概念格记为L(KC)。对于概念格中的概念数量,由于概念格本质上是集合,将其中元素的数目记为|L(KC)|。相似地,由这种概念格形成的面向对象三支概念格记为OEL(KC),面向属性三支概念格记为AEL(KC)。

定理1在属性粒化的过程中,随着属性粒度层次的细化,属性集中元素的增多,概念格中概念的数量不会减少。

证明在属性粒化过程中,对于任意属性分解过程a→{a1,a2,…,al},若该属性分解导致概念格中元素减少,则为在原概念格中存在概念的内涵B,a∈B的基础上,新概念格中不存在概念的内涵BC,令BC∩{a1,a2,…,al}≠∅。

对于新属性集中的元素∀ap(1≤p≤l)∈{a1,a2,…,al},设A=(M∩MC)∪{ap},则因为(A*C)*C=A*C*C,且(A*C*C)*C=A*C*C*C=A*C,因此(A*C,A*C*C)是一个概念格,因为A⊆A*C*C,所以ap∈A*C*C,则在新的概念格中存在概念内涵A*C*C∩{a1,a2,…,al}≠∅。以上假设不成立,即任意属性分解均不会造成概念格中元素减少,原定理得证。

类似地,有如下定理:

定理2在属性粒化的过程中,随着属性粒度层次的细化,属性集中元素增多,面向对象三支概念格中概念的数量不会减少。

定理3在属性粒化的过程中,随着属性粒度层次的细化,属性集中元素的增多,面向属性三支概念格中概念的数量不会减少。

3.2 细化系数

为了研究属性聚类对三支概念的影响,需要在同一对象集下,进一步建立属性聚类前后三支概念的联系。对于属性集M={m1,m2,…,m|M|},聚类后表示为MR={([m]R)1,([m]R)2,…,([m]R)k}(k≤|M|),其中,R为聚类关系,∀1≤p,q≤k,且p≠q,根据等价类与集合的性质,([m]R)p∩([m]R)q=∅。定义一般属性聚类中的算子与负算子,对于X⊆G和A⊆MR:如果在定义事物的时候,选择描述事物的关键词越多,分类越细致,对于事物的定义就会越精确。相似地,概念格在不同的属性层次移动,由粗到细的时候,概念也会由粗到细,得到更加精确的概念。概念格中概念的数量也会随之变化。根据定理1,较粗属性层次对应的概念格中的概念数量会大于或等于较细属性层次对应的概念格中概念的数量,因此可以通过比较层次移动时概念格中概念数量的变化来比较属性粒化的效果。

定义1对于属性粒化层次C1和C2,若存在偏序关系C1≤C2,即前者是后者的细化,在度量细化时,定义细化系数eLC如式(1)所示:

(1)

细化系数eLC越大,表明新的属性层次产生了越多的新概念,此次属性粒化越有效。

相似地,根据定理2和定理3,可以定义出与以上细化系数相同的面向对象细化系数和面向属性细化系数。

定义2对于属性粒化层次C1和C2,若存在偏序关系C1≤C2,即前者是后者的细化,在度量细化时,定义面向对象细化系数eOELC如式(2)所示:

(2)

定义3对于属性粒化层次C1和C2,若存在偏序关系C1≤C2,即前者是后者的细化,在度量细化时,定义面向属性细化系数eAELC如式(3)所示:

(3)

以下用示例说明2种细化系数的用法。

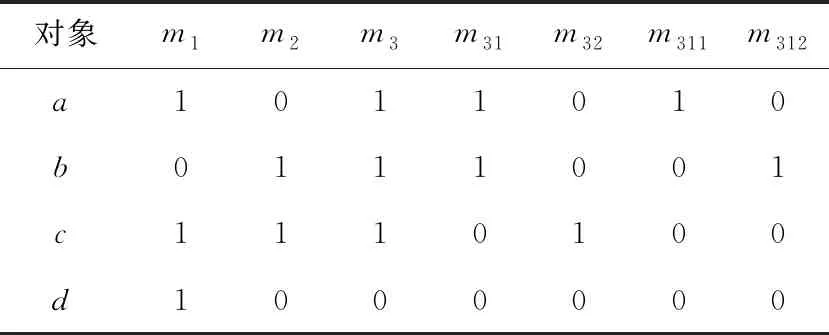
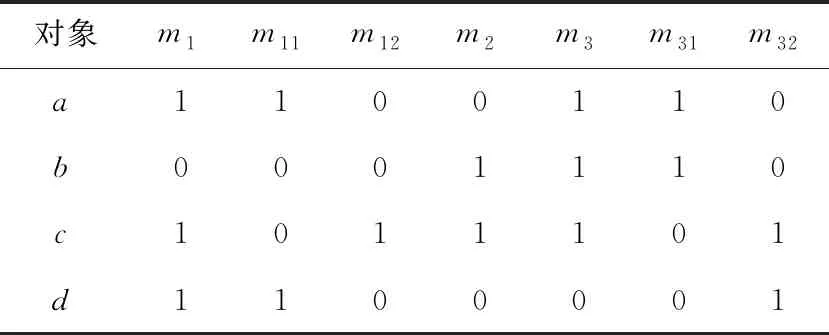
例1现有一购物网站搜索场景利用如表2所示形式背景K=(G,M,I)表示,其中,M={m1,m2,m3},MC1={m1,m2,m31,m32},MC2={m1,m2,m31,m321,m322}。对象代表4种不同的鞋品,属性代表商品的特征,m1,m2和m3分别代表网面材质、黑色和安踏品牌,且粒度树如图2所示。对于存在偏序关系C2

Figure 2 Granularity tree of table 2

Table 2 Formal background K=(G,M,I) for example 1

计算可得:

同理,|OEL(KC2)|=12,eOELC2=12/11>1;|AEL(KC2)|=15,eOELC2=3/2>1。该属性粒化在C2上存在意义。

4 不存在偏序关系的不同粒度层次

在实际应用中,经常使用属性粒化对现有概念进行细化,而属性细化方向的选择则与属性粒化的效率息息相关,细化方向选择的不同会导致属性粒化效率的差别,例如,在试图细化“牛仔裤”这个概念的时候,存在多种细化方向,显然,将“蓝色”细化为“深蓝色”和“浅蓝色”相较于将“红色”细化为“浅红色”和“深红色”更加有效。

例2现有一购物网站搜索场景利用如表3所示的形式背景K=(G,M,I)表示,其中,M={m1,m2,m3},MC1={m1,m2,m31,m32},MC3={m11,m12,m2,m3}。对象代表4种不同的鞋品,属性代表商品的特征,m1,m2和m3分别代表网面材质、黑色和安踏品牌,且粒度树如图3所示。不存在偏序关系的属性粒化层次及生成的新形式背景KC1=(G,MC1,IC1)和KC3=(G,MC3,IC3),m11和m12分别代表全网面鞋和半网面鞋,m31和m32分别代表安踏品牌休闲系列与安踏品牌运动系列。

Figure 3 Granularity tree of table 3

Table 3 Formal background K=(G,M,I) for example 2

Table 4 Formal background K=(G,M,I) for example 3

计算可得:

|OEL(KC3)|=10,eOELC3=5/4

|AEL(KC3)|=10,eAELC3=10/7=eAELC1

因此,属性粒化方向C1优于C3。

在具体的现实操作中,细化方向的选择往往更加复杂,且相较于以上实例更加抽象和不直观,因此通过细化算子来度量不存在偏序关系的不同粒度层次的优劣,以此来选择粒度层次进行进一步细化,从而避免冗余的计算和资源的浪费,是十分有必要的。

5 算法

5.1 理论依据

以下一组定理是获取面向对象三支概念格与面向属性三支概念格的理论依据。

定理4设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(X,B)是一个反概念,那么(X,(A,B))一定是一个OE概念,记由此得到的概念集合为O1。

定理5设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,B)是一个反概念,且Y为X的最小上界,X不属于FL(K)的外延集,那么(X,(A,B))一定是一个OE概念,记由此得到的概念集合为O2。

定理6设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,B)是一个反概念,且X为Y的最小上界,Y不属于L(K)的内涵集,那么(Y,(A,B))一定是一个OE概念,记由此得到的概念集合为O3。

定理7设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,B)是一个反概念,且X,Y均为X∩Y的最小上界,X不属于FL(K)的外延集,Y不属于L(K)的内涵集,那么(X∩Y,(A,B))一定是一个OE概念,记由此得到的概念集合为O4。

定理8设K=(G,M,I)是一个形式背景,则OEOL(K)=O1∪O2∪O3∪O4。

定理9设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,A)是一个反概念,那么((X,Y),A)一定是一个AE概念,记由此得到的概念集合为A1。

定理10设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,B)是一个反概念,且B为A的最小上界,A不属于FL(K)的内涵集,那么((X,Y),A)一定是一个AE概念,记由此得到的概念集合为A2。

定理11设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,B)是一个反概念,且A为B的最小上界,B不属于L(K)的内涵集,那么((X,Y),B)一定是一个AE概念,记由此得到的概念集合为A3。

定理12设K=(G,M,I)是一个形式背景,若(X,A)是一个概念且(Y,B)是一个反概念,且A,B均为A∩B的最小上界,A不属于FL(K)的内涵集,B不属于L(K)的内涵集,那么((X,Y),A∩B)一定是一个AE概念,记由此得到的概念集合为A4。

定理13设K=(G,M,I)是一个形式背景,则AEPL(K)=A1∪A2∪A3∪A4。

5.2 获取eOELC算法

根据以上理论可以获取eOELC,如算法2所示。

算法2 获取eOELC输入:概念格L(K),L(KC)与反概念格FL(K),FL(KC)。输出:参数eOELC。步骤1 初始化O1=⌀,O2=⌀,o1=0,o2=0;步骤2 令LpG∩FqG=W;if W=LpG且W=FqG then O1=O1∪(W,(LpM,FqM)); /*LpG和LpM分别表示在L(K)中概念的外延和内涵,FqG和FqM分别表示在FL(K)中反概念的外延和内涵*/else if W=LpG,W≠FqG且FqG为W最小上界 then O1=O1∪(W,(LpM,FqM)); else if W≠LpG,W=FqG且LpG为W最小上界 then W1=W1∪(W,(LpM,FqM));else if W≠LpG,W≠FqG且LpG与FqG均为W最小上界 then O1=O1∪(W,(LpM,FqM));end ifo1为O1中元素的个数;步骤3 令LpGC∩FqGC=V;if V=LpGC且V=FqGC then O2=O2∪(V,(LpMC,FqMC)); /*LpGC和LpMC分别表示在L(KC)中概念的外延和内涵,FqGC和FqMC分别表示在FL(KC)中反概念的外延和内涵*/else if V=LpGC,V≠FqGC且FqGC为V最小上界 then O2=O2∪(V,(LpMC,FqMC));else if V≠LpGC,V=FqGC且LpGC为V最小上界 then O2=O2∪(V,(LpMC,FqMC));else if V≠LpGC,V≠FqGC且LpGC与FqGC均为V最小上界 then O2=O2∪(V,(LpMC,FqMC));end if步骤4 eOELC=o2/o1;步骤5 输出eOELC

例3现某购物网站需要对搜索机制改良,对10件短袖的标签进行细分,根据最新网络关键词捕捉报告,近期“全棉”与“含棉混合面料”的区别引起消费者广泛讨论,故生成如图4所表示的粒度树。

Figure 4 Granularity tree of commodity research

根据粒度树与“商品-标签”对应关系,有如表4所示形式背景K=(G,M,I)和KC=(G,MC,I),其中,G={α,β,…,τ},M={n1,n2,n3,n4},MC={n1,n2,n3,n41,n42}。

现以此例,从准确性和效率性评估算法2(与直接计算作比较)。

利用直接计算方法,求得OEL(K)需要进行算子计算(包括正算子和负算子)544次,交集运算256次,比较运算512次,最后得出|OEL(K)|=33;求得OEL(KC)需要进行算子计算(包括正算子和负算子)2 112次,交集运算1 024次,比较运算2 048次,最后得出|OEL(KC)|=52。共计使用算子计算2 656次,交集运算1 280次,比较运算2 560次。最终计算得出eOELC=52/33。

利用本文的改进算法Next Clousure算法计算概念格与反概念格。计算K的概念格使用算子运算32次,比较运算16次;计算KC的概念格使用算子运算64次,比较运算32次。利用2个计算结果进一步计算eOELC的过程中,使用交集运算1 280次,比较运算256次,最终输出eOELC=52/33。

在实验过程中,需要尤为注意的是,算子计算的复杂度与其他计算是不可同日而语的。以本数据集为例,一次算子计算包含4～50次的运算;而一次比较计算至多只涉及5次对应计算。因此,效率性的评估以算子计算的数目为主要评价指标。

综上,在计算eOELC时,使用本文提出的算法相较直接计算方法大幅减少了正算子及负算子的计算量,极大降低了计算复杂度。2次计算输出的eOELC相等。算法2相比直接计算方法在保证准确性的前提下,极大提升了计算效率。

5.3 获取eAELC算法

根据以上理论可以获取eAELC,如算法3所示。

算法3 获取eAELC输入:概念格L(K),L(KC),与反概念格FL(K),FL(KC)。输出:参数eAELC。步骤1 初始化A1=⌀,A2=⌀,a1=0,a2=0;步骤2 令LpM∩FqM=N;if N=LpM且N=FqM then A1=A1∪((LpG,FqG),N); /*LpG和LpM分别表示在L(K)中概念的外延和内涵,FqG和FqM分别表示在FL(K)中反概念的外延和内涵*/else if N=LpM,N≠FqM且FqM为N最小上界 then A1=A1∪((LpG,FqG),N);else if N≠LpM,N=FqM且LpM为N最小上界 then A1=A1∪((LpG,FqG),N);else if N≠LpM,N≠FqM且LpM,FqM均为N最小上界 then A1=A1∪((LpG,FqG),N);end ifa1为A1中元素的个数;步骤3 令LpMC∩FqMC=Q;if Q=LpMC且Q=FqMC then A2=A2∪((LpGC,FqGC),Q);else if Q=LpMC,Q≠FqMC且FqMC为Q最小上界 then A2=A2∪((LpGC,FqGC),Q);else if Q≠LpMC,Q=FqMC 且LqMC为Q最小上界 then A2=A2∪((LpGC,FqGC),Q);else if Q≠LpMC,Q≠FqMC且LpMC,FqMC均为Q最小上界 then A2=A2∪((LpGC,FqGC),Q);end ifa2为A2中元素的个数;步骤4 eAELC=a2/a1;步骤5 输出eAELC

接例3,从准确性和效率性评估算法3(与直接计算作比较)。

利用直接计算方法,求得AEL(K)需要进行算子计算64次,交集运算16次,比较运算32次,最后得出|AEL(K)|=12;求得AEL(KC)需要进行算子计算(包括正算子和负算子)128次,交集运算32次,比较运算64次,最后得出|AEL(KC)|=17。共计使用算子计算192次,交集运算48次,比较运算96次。最终计算得出eAELC=17/12。

利用本文改进算法Next Clousure算法计算概念格与反概念格。计算K的概念格使用算子运算32次,比较运算16次;计算KC的概念格使用算子运算64次,比较运算32次。利用2个计算结果进一步计算eAELC过程中,使用交集运算1 280次,比较运算256次,最终输出eAELC=17/12。2次计算输出的eAELC相等。

综上,在计算eAELC时,使用本文提出算法相比直接计算方法减少了正算子及负算子的计算量。算法3相比直接计算方法在保证准确性的前提下,极大地提升了计算效率。