基于混合策略改进的蛇优化算法及其应用*
2024-04-23梁昔明史兰艳
梁昔明,史兰艳,龙 文
(1.北京建筑大学理学院,北京 102616;2.贵州财经大学数学与统计学院,贵州 贵阳 550025)
1 引言
近些年,越来越多的群智能优化算法被提出,比如樽海鞘优化算法[1]、灰狼优化算法[2,3]、蝴蝶优化算法[4-6]和鲸鱼优化算法WOA(Whale Optimization Algorithm)[7-10]等。这些算法通过模拟自然界中鱼群、鸟群、蜂群、狼群和细菌群等群体的行为,利用群体间的信息交流与合作,以简单有限的个体间互动来搜索优化问题的最优解。群智能优化算法相较于传统的优化算法,无需计算梯度,只需在搜索空间内不断地进行个体位置更新以求得最优解,所以群智能优化算法的适用范围更加广泛,已被应用于多个领域。蛇优化SO(Snake Optimization)算法是由Hashim等人[11]于2022年提出的一种模仿蛇特殊交配行为的新型群智能优化算法。蛇优化算法遵循蛇的交配行为:当温度较低且有食物时蛇进行交配,否则蛇只会寻找食物或吃掉现有的食物。蛇优化算法的搜索过程分为3个阶段:探索食物阶段、靠近食物阶段和战斗或交配阶段。在探索食物阶段,蛇只在当前环境中寻找食物。靠近食物阶段是指在有食物但温度很高的情况下,蛇只会专注于吃现有的食物。如果食物充足而且环境寒冷,蛇进入战斗或交配阶段,该阶段有2种模式:战斗模式或交配模式。在战斗模式中,每只雄性为了得到最好的雌性而战斗,而每只雌性则会努力选择最好的雄性;在交配模式中,如果交配成功,雌性蛇就会产卵,孵化出新的蛇。蛇优化算法与其他群智能优化算法一样也存在易陷入局部最优的不足,本文通过引入维度选择策略、选择交配策略和重新分组策略来修改蛇优化算法,提出了一种基于混合策略改进的蛇优化SSO(Supplant Snake Optimization)算法。
2 基本蛇优化算法
对于无约束优化问题:
minf(X)
其中,f(X)是D维的目标函数,蛇优化算法包含如下9个基本步骤,步骤中所涉及常数参数的取值均与文献[11]中常数参数的取值相同。
(1)初始化种群。
与所有的元启发式算法一样,蛇优化算法首先生成均匀分布的随机种群。初始种群按式(1)产生:
Xi(0)=Xmin+rand×(Xmax-Xmin)
(1)
其中,Xi(0)表示第i个个体的初始位置,i=1,2,…,N,N代表种群规模,Xmin和Xmax分别表示搜索空间的下限与上限,rand表示0到1之间的随机数。
(2)分组种群。
将种群分为雄性种群和雌性种群2组。本文假设雄性个体数量和雌性个体数量各占种群规模N的50%,雄性种群表示为:
Xm={X1(0),X2(0),…,XNm(0)}
(2)
其中,Nm=N/2表示雄性种群规模。
雌性种群表示为:
Xf={XNm+1(0),XNm+2(0),…,XN(0)}
(3)
雌性种群规模记为Nf=N-Nm。
(3)计算适应度值。
取优化问题的目标函数f(X)为适应度函数,计算种群中每个个体的适应度值,将种群中适应度值最小个体的位置记为食物的位置Xfood,将雄性种群中适应度值最小个体的位置记为Xbest,m,雌性种群中适应度值最小个体的位置记为Xbest,f。
(4)计算温度与食物数量。
蛇交配行为受温度和食物数量的影响,蛇优化算法要根据当前迭代的温度和食物数量来确定种群中每个个体的行为。当前迭代时的温度Temp和食物数量Q根据式(4)和式(5)计算:
(4)
(5)
其中,t表示当前迭代次数,T表示最大迭代次数,c1为常数,通常取0.5。
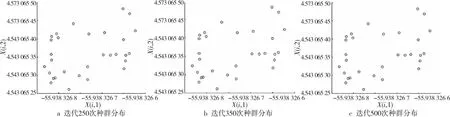
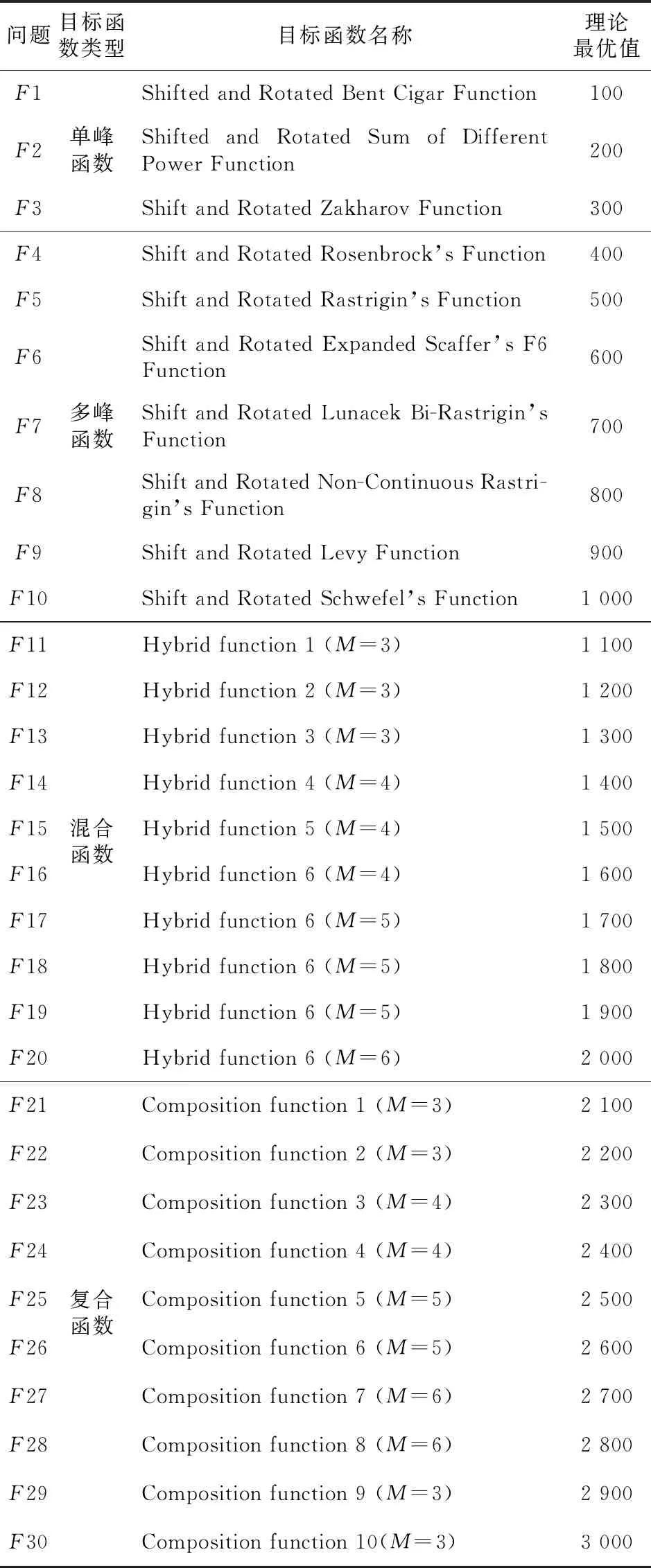
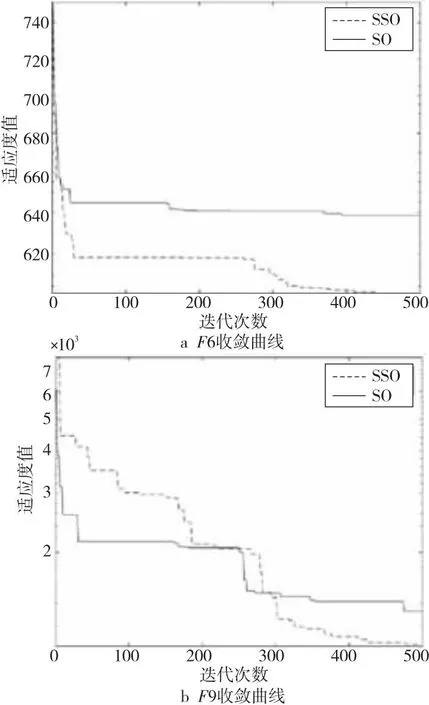
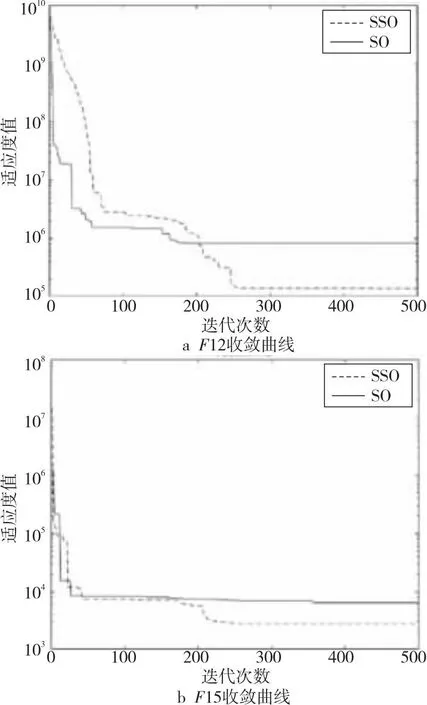
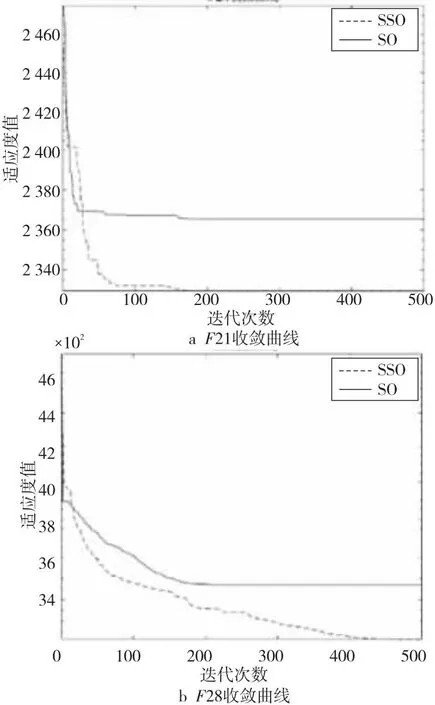
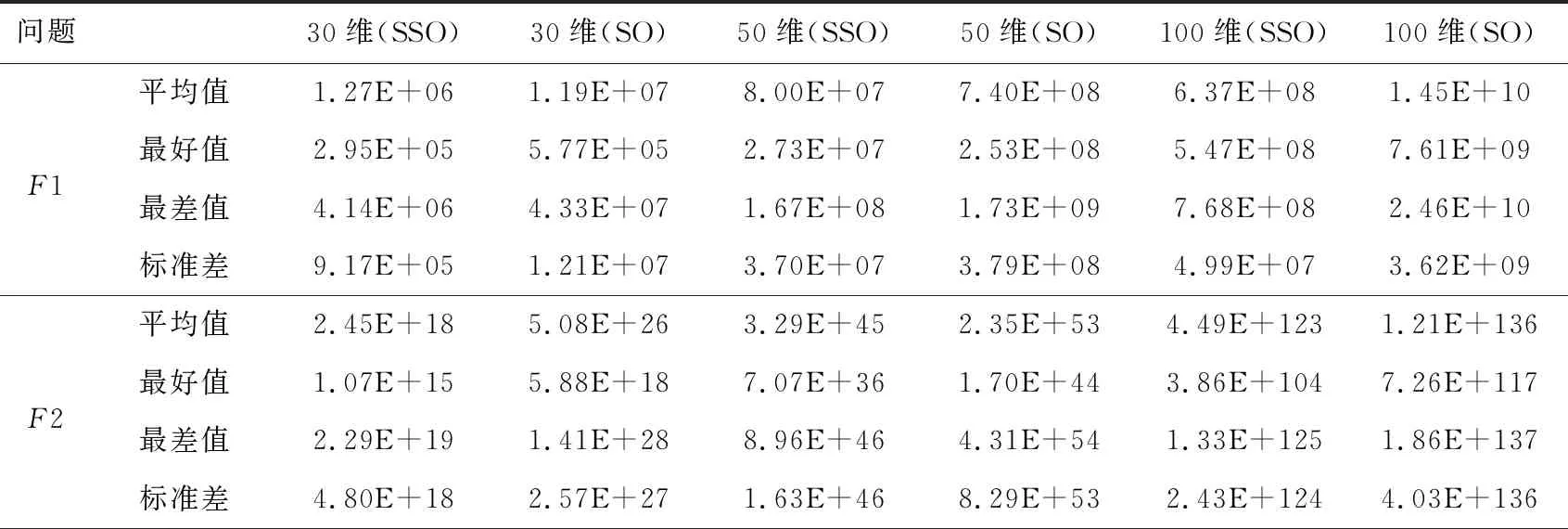
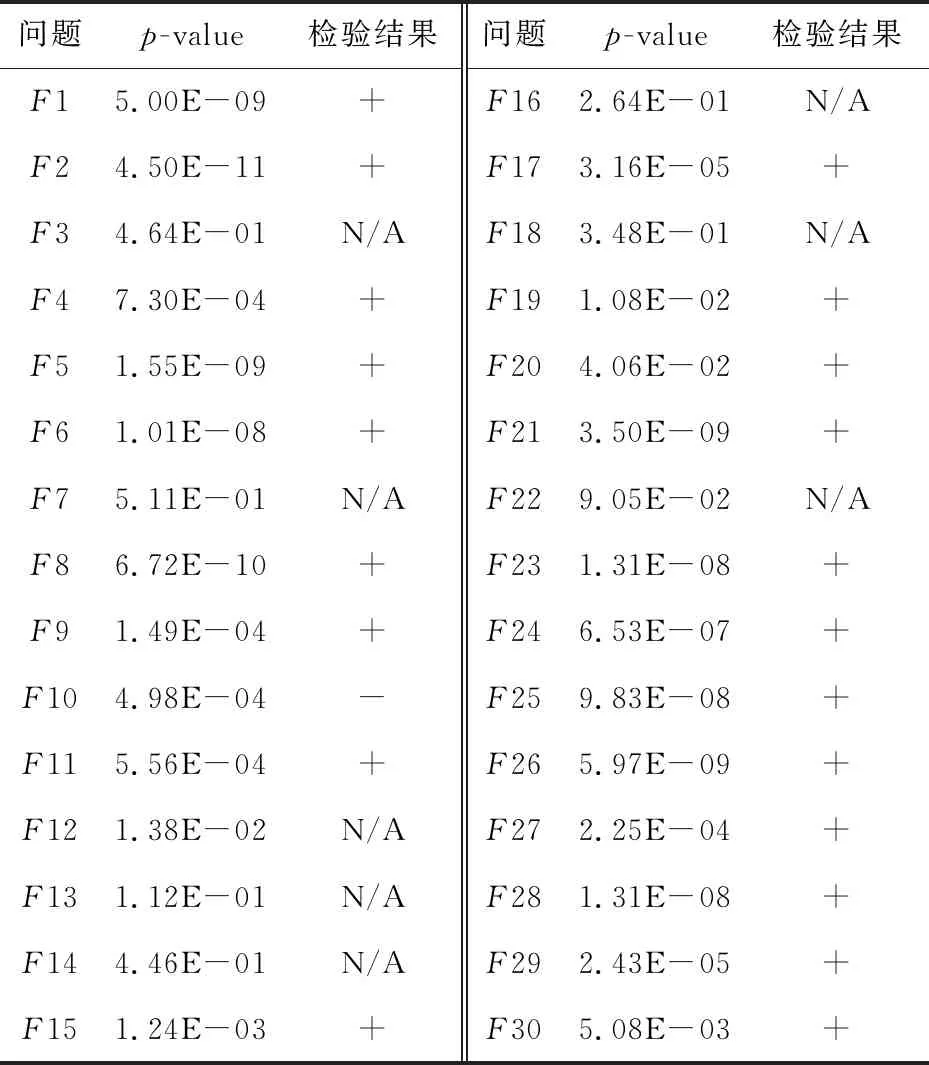
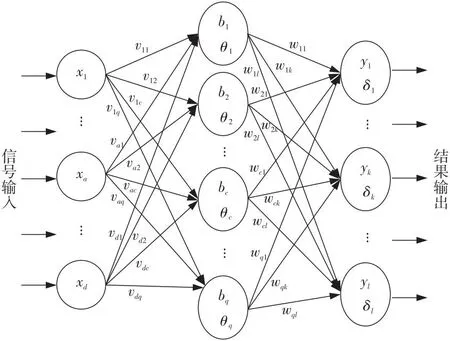
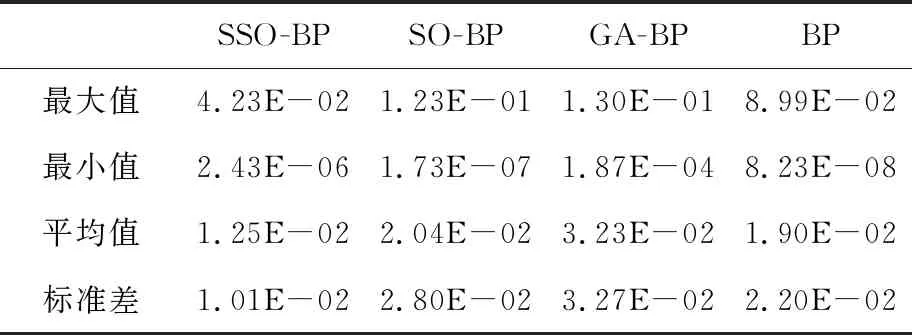
如果Q (5)探索食物。 每条蛇个体通过选择随机位置寻找食物,即按式(6)和式(7)来更新它们的位置: Xi,m(t+1)=Xrand,m(t)±c2×Am× [(Xmax-Xmin)×rand+Xmin] (6) Xi,f(t+1)=Xrand,f(t)±c2×Af× [(Xmax-Xmin)×rand+Xmin] (7) 其中,Xi,m(t)表示t次迭代第i个雄性个体的位置,Xi,f(t)表示t次迭代第i个雌性个体的位置,Xrand,f(t)与Xrand,m(t)分别表示t次迭代随机选取的雌性和雄性个体的位置,rand是0到N/2之间的随机整数,±表示随机生成的标志方向算子,也被称为多样性因子,它提供了增加或减少位置解的可能性,从而在给定搜索空间的所有可能方向上进行良好的扫描。c2为常数,通常取0.05。Am和Af分别表示雄性个体Xi,m(t)和雌性个体Xi,f(t)寻找食物的能力,由式(8)和式(9)计算得出: (8) (9) 其中,frand,m、frand,f、fi,m和fi,f分别表示Xrand,m(t)、Xrand,f(t)、Xi,m(t)和Xi,f(t)的适应度值。 (6)靠近食物。 每条蛇个体按如式(10)所示位置更新公式靠近食物: Xi,n(t+1)=Xfood(t)±c3× Temp×(Xfood(t)-Xi,j(t))×rand (10) 其中,Xi,n(t)表示t次迭代第i个个体的位置,n取m或f,分别表示雄性或雌性,Xfood(t)表示t次迭代食物的位置,c3为常数,通常取2。 (7)战斗或交配。 在该阶段,每条蛇个体根据随机生成的概率p来选择战斗模式或交配模式进行位置更新。 如果p>0.6,蛇个体选择战斗模式,即按式(11)和式(12)进行位置更新: Xi,m(t+1)=Xi,m(t)±c3×Fm× rand×(Q×Xbest,f(t)-Xi,m(t)) (11) Xi,f(t+1)=Xi,f(t)±c3×Ff× rand×(Q×Xbest,m(t)-Xi,f(t)) (12) 其中,Xbest,m(t)和Xbest,f(t)分别表示t次迭代适应度值最小雄性个体和雌性个体的位置,Fm和Ff分别表示雄性个体和雌性个体在位置Xi,m(t)和Xi,f(t)处的战斗能力,由式(13)和式(14)计算得出: (13) (14) 其中,fbest,f和fbest,m分别表示Xbest,f(t)和Xbest,m(t)的适应度值。 如果p≤0.6,蛇个体选择交配模式,即按式(15)和式(16)进行位置更新: Xi,m(t+1)=Xi,m(t)+c3× Mm×rand×(Q×Xi,f(t)-Xi,m(t)) (15) Xi,f(t+1)=Xi,f(t)+c3× Mf×rand×(Q×Xi,m(t)-Xi,f(t)) (16) 其中,Mm和Mf分别表示雄性个体和雌性个体在位置Xi,m(t)和Xi,f(t)处的交配能力,由式(17)和式(18)计算得出: (17) (18) 根据随机数egg∈{-1,1}判断交配是否成功,如果egg=1,则交配成功,对适应度值最大的雄性个体Xworst,m(t)和雌性个体Xworst,f(t)按式(19)和式(20)进行位置更新: Xworst,m(t+1)=Xmin+rand×(Xmax-Xmin) (19) Xworst,f(t+1)=Xmin+rand×(Xmax-Xmin) (20) (8)选择个体。 比较每个个体位置更新前后的适应度值,选择适应度值小的位置进入下一次迭代。 (9)检查终止条件。 判定迭代次数是否达到指定的最大迭代次数,如果达到,则终止迭代,输出Xfood以及ffood;否则,根据个体适应度值重新确定Xfood,Xbest,m(t)以及Xbest,f(t),返回步骤(4)继续迭代。 基本蛇优化算法的伪代码如算法1所示。 算法1 蛇优化算法输入:最大迭代次数T,种群规模N,搜索空间上下限Xmax、Xmin。输出:输出食物位置Xfood及其适应度值ffood。步骤1 令t=0;步骤2 利用式(1)生成初始化种群X;步骤3 利用式(2)和式(3)将种群X分为雄性种群Xm和雌性种群Xf;步骤4 计算个体的适应度值;步骤5 while t 基本蛇优化算法在迭代后期会出现勘探能力减弱、个体位置停滞等现象,算法会过早收敛或陷入局部最优。本文引入维度选择策略、选择交配策略和重新分组策略来修改基本蛇优化算法,提出一种基于混合策略改进的蛇优化算法,记为SSO。 在基本蛇优化算法中,当食物数量与温度满足蛇交配所需要的条件时,每条蛇个体就会进入战斗或交配阶段以战斗模式或交配模式进行位置更新。通过大量的数值实验观察发现,基本蛇优化算法在该阶段位置更新产生的新个体在进行选择个体时几乎都会被淘汰,即前后2次迭代的个体位置几乎相同,出现个体位置停滞现象。 图1以单峰测试问题F3为例列出当种群规模N=30、问题维度D=2、最大迭代次数T=500时基本蛇优化算法迭代250、350、500次个体位置分布情况,横坐标X(i,1)表示第i个个体第1维的位置,纵坐标X(i,2)表示第i个个体第2维的位置。从图1可以看出基本蛇优化算法在战斗或交配阶段个体位置几乎没有变化,出现个体位置停滞现象,以致于蛇优化算法在迭代后期搜索性能下降。为了克服个体位置停滞现象,本文在该阶段引入维度选择策略。 Figure 1 Population distributions of standard unconstrained optimization problems F3 obtained by the SO 维度选择策略是指每个个体在不同维度上各生成不同的随机概率p(j)(j代表维度),由概率p(j)决定该个体在该维度的位置更新模式,每个维度的概率p(j)是独立的[12]。基本蛇优化算法在战斗或交配阶段中每条蛇个体在不同维度的位置更新模式都是相同的;引入维度选择策略,每个个体在不同维度的位置更新模式可能不同,该策略能有效避免迭代后期个体位置停滞现象的发生。 战斗或交配阶段引入维度选择策略位置更新公式如式(21)和式(22)所示: (21) (22) 蛇优化算法在战斗或交配阶段进行局部搜索,蛇个体逐渐靠近当前最优雄性个体或雌性个体,算法在该阶段探索能力较弱,易陷入局部最优。为了提高蛇优化算法在战斗或交配阶段的探索能力,本文在该阶段引入选择交配策略。 选择交配策略是在战斗或交配阶段先根据适应度值的大小分别从雄性种群和雌性种群中选出适应度值小的Nm/2个和Nf/2个蛇个体,然后利用式(21)和式(22)分别更新所选出的蛇个体的位置,剩余雄性个体和雌性个体则利用探索食物阶段的位置更新式(6)和式(7)进行位置更新。因为蛇优化算法在探索食物阶段的勘探能力强,在战斗或交配阶段选择适应度值大的部分雄性个体和雌性个体利用探索食物阶段的位置更新公式进行位置更新可有效增强蛇优化算法迭代后期的勘探能力。 为了增加种群个体的多样性,提高算法寻优能力,本文引入重新分组策略,即对种群每迭代10次后重新进行分组,将整个种群随机打乱并重新分成雄性种群和雌性种群。 本文在蛇优化算法中引进上述3种改进策略,得到基于混合策略改进的蛇优化SSO算法,其迭代步骤如下: 步骤1:初始化最大迭代次数T与种群规模N,令t=0; 步骤2:按式(1)产生初始化种群; 步骤3:按式(2)和式(3)分组种群; 步骤4:根据适应度函数f(X)计算个体适应度值; 步骤5:按式(4)和式(5)计算温度Temp和食物数量Q; 步骤6:如果Q<0.25,进入步骤7;否则,进入步骤8; 步骤7:每条蛇个体按式(6)和式(7)更新它们的位置,转步骤11; 步骤8:如果Temp≥0.6,进入步骤9;否则,进入步骤10; 步骤9:每条蛇个体按式(10)更新位置,转步骤11; 步骤10:根据适应度值分别从雄性种群和雌性种群中选出适应度值小的Nm/2个和Nf/2个蛇个体,然后利用式(21)和式(22)分别更新所选出的蛇个体的位置,剩余雄性个体和雌性个体则利用探索食物阶段的位置更新式(6)和式(7)进行位置更新,转步骤11; 步骤11:比较个体位置更新前后的适应度值,保留适应度值小的个体位置,更新Xfood、Xbest,m以及Xbest,f,并令t=t+1; 步骤12:判定t≥T是否成立,若是,则终止迭代,输出Xfood以及ffood;若否,进入步骤13; 步骤13:判断t是否为10的倍数,若是,将种群随机打乱,按式(2)和式(3)重新进行分组并返回步骤5;若否,直接返回步骤5。 为了评估改进蛇优化SSO算法的有效性,本文使用文献[13]中的30个无约束标准测试问题进行测试。这30个问题涵盖4种类型的目标函数:单峰函数、多峰函数、混合函数和复合函数。 表1描述了每个标准测试问题的目标函数类型、名称及其理论最优值。 Table 1 Objective function information for standard test problems 选取的对比算法有鲸鱼优化算法WOA[7]、基本蛇优化SO算法[11]、Moth-Flame优化MFO(Moth Flame Optimization)算法[14],哈里斯鹰优化HHO(Harris Hawk Optimization)算法[15],热交换优化TEO(Thermal Exchange Optimization)算法[16,17]以及蚱蜢优化算法GOA(Grasshopper Optimization Algorithm)[18]。 数值实验中,初始参数设置与文献[11]的表1中初始参数设置相同,即设置SSO算法的最大迭代次数为500,种群规模为30,标准测试问题目标函数的维度均设为30维。为避免偶然性,SSO算法对每一个问题进行30次独立求解,并取30次求解所得问题的目标函数值的最好值、最差值、平均值和标准差,结果如表2所示,对比算法的相关数据参见文献[11]中表4。 Table 2 Results of objective function values of 30 standard test problems by SSO algorithm 由表2数据和文献[11]中表4数据对比可知,基于混合策略改进的蛇优化SSO算法对18个标准测试问题(F1、F2、F4~F6、F8、F9、F11~F13、F15、F17、F19、F21、F23~F25、F29)求解所得目标函数值的平均值、最好值、最差值和标准差都好于6种对比算法。对比7种算法所得平均目标函数值,SSO算法对25个问题(F1、F2、F4~F9、F11~F17、F19~F21、F23~F26、F28~F30)所得结果最小,对1个问题(F18)所得结果次小,对3个问题(F3、F22、F27)所得结果第三小。从7种算法所得目标函数值的标准差来看,SSO算法对21个问题(F1、F2、F4~F6、F8、F9、F11~F13、F15、F17、F19、F21、F23~F27、F29、F30)所得结果最小,对5个问题(F7、F14、F16、F20、F28)所得结果次小,对1个问题(F18)所得结果第三小。对比7种算法所得最小目标函数值,SSO算法对24个问题(F1、F2、F4~F6、F8~F17、F19~F25、F28、F29)所得结果最小,对5个问题(F3、F7、F18、F26、F30)所得结果次小,对1个问题(F27)所得结果第三小。基于混合策略改进的蛇优化SSO算法对比于基本蛇优化SO算法,有20个问题(F1、F2、F4~F6、F8、F9、F11~F15、F17、F19、F21、F23~F25、F28、F29)的目标函数值的平均值、最好值、最差值和标准差都更小,其中对问题F1、F2、F9、F12、F13所得目标函数值的平均值、最好值、最差值和标准差明显小于SO算法所得结果;对问题F1、F2、F9、F12~F15、F17、F19、F26、F29、F30所得目标函数值的平均值明显小于SO算法的相应结果;对问题F1、F2、F5、F9、F11~F15、F19、F26、F30所得目标函数值的标准差明显小于SO算法所得结果;对问题F1~F3、F9、F10、F12~F15所得目标函数值的最好值明显小于SO算法的相应结果。对于问题F3、F7、F16、F20、F26、F27、F30,SSO算法与SO算法所得目标函数值结果相近。对于问题F7、F16、F20、F26、F30,SSO算法所得目标函数值结果略大于SO算法的相应结果,但小于其他5种算法的相应结果。SSO算法所得问题F18的目标函数值结果大于SO算法的相应结果,但小于其他5种算法的相应结果。对于问题F10和F22,SSO算法所得目标函数值结果不如其他算法的相应结果好。综上,利用基于混合策略改进的蛇优化SSO算法求解30个标准无约束优化问题的结果大部分都优于对比的算法。 图2~图5给出了不同函数类型部分标准测试问题的收敛曲线,包括标准测试问题F1、F3、F6、F9、F12、F15、F21、F28。通过观察图2~图5以及文献[11]中图5~图7对应标准测试问题的收敛曲线可知,相比于SO算法等6种对比算法,SSO算法求解大部分标准测试问题具有更快的收敛速度和更高的收敛精度。 Figure 2 Convergence curves of standard unconstrained optimization problems F1 and F3 by SSO and SO algorithms Figure 3 Convergence curves of standard unconstrained optimization problems F6 and F9 by SSO and SO algorithms Figure 4 Convergence curves of standard unconstrained optimization problems F12 and F15 by SSO and SO algorithms Figure 5 Convergence curves of standard unconstrained optimization problems F21 and F28 by SSO and SO algorithms 为了比较SSO算法与SO算法对于不同维度问题的求解能力,将问题F1~F30的维度分别设置为30,50,100,利用2种算法分别对它们进行求解。2种算法的种群规模N均设置为30,最大迭代次数T均设置为500。为避免偶然性,2种算法对不同维度的每个问题分别独立求解30次,取30次独立求解所得目标函数值的最好值、最差值、平均值及标准差进行对比,相关数值结果如表3所示。 Table 3 Results of standard test problems with different dimensions by SSO and SO algorithms 从表3可以看出,对于问题F1、F2、F4、F6、F8、F12、F13、F19、F23~F28、F30,当维度分别为30,50及100时,SSO算法所得目标函数值都好于SO算法的相应结果。对于问题F1、F2,问题维度越高,算法所求得的目标函数值与理论最优值相差越明显,但SSO算法所得目标函数值明显好于SO算法的相应结果。对于问题F7、F14、F18、F29,当维度是30维时,SSO算法所得目标函数值差于SO算法的相应结果,但随着问题维度增加,SSO算法所得目标函数值好于SO算法的相应结果。对于问题F15、F17、F20,当问题维度为30时,SSO算法所得目标函数值好于SO算法的相应结果,但随着问题维度的增加,SSO算法所得目标函数值略差于SO算法的相应结果。综上,相比SO算法,SSO算法在求解大部分高维问题上占有优势。 为了从统计学上比较基于混合策略改进的蛇优化SSO算法与基本蛇优化SO算法有无明显差异,本节设置2种算法的最大迭代次数均为500,种群规模均为30,问题的维度均为30维,使用Wilcoxon秩和[19]进行了非参数检验,通过计算p-value的大小判断2种算法的差异是否明显。p-value的值越小,说明2种算法的差别越明显;若p-value大于0.05,则说明2种算法性能基本相同,不存在明显差异。计算所得的p-value数值如表4所示,其中“+”表示SSO算法的性能优于SO算法,“-”表示SSO算法的性能劣于SO算法,“N/A”表示2种算法的性能差异不明显。 Table 4 Results of Wilcoxon rank sum test 从表4可以看出,有22个问题(F1,F2、F4~F6、F8~F11、F15、F17、F19~F21、F23~F30)的p-value小于0.05,结合前面数值实验结果可知,22个问题中有17个问题(F1,F2、F4~F6、F8、F9、F11、F15、F17、F19、F21、F23~F25、F28、F29)利用SSO算法求解得到的目标函数值明显好于SO算法求解所得到的相应结果。对于问题F3、F7、F12~F14、F16、F18、F22,p-value均大于0.05,说明2种算法在求解这些问题时差异不明显。问题F26和F30的p-value都小于0.05,虽然数值实验结果表明利用SSO算法求解这2个问题所得目标函数的最好值略大于SO算法求解的相应结果,但利用SSO算法求解这2个问题所得目标函数的平均值、最差值和标准差都明显小于SO算法求解的相应结果。问题F10秩和检验结果小于0.05,SSO算法求解问题F10得到的目标函数值不如SO算法的好,说明SO算法在求解问题F10时比SSO算法有优势。综上,相比基本蛇优化SO算法,基于混合策略改进的蛇优化SSO算法在求解大部分标准测试问题上性能更好。 基本BP(Back Propagation)神经网络由输入层、隐藏层和输出层组成,如图6所示。 Figure 6 Basic BP neural network 图6中xa表示输入层输入,bc表示隐含层输入,yk表示输出层输入,vac和wck分别表示输入层到隐藏层和隐藏层到输出层的权重。θc和δk分别表示隐含层神经元的阈值与输出层神经元阈值,a=1,2,…,d,c=1,2,…q,k=1,2,…l,d表示基本BP神经网络输入层节点的个数,q表示隐含层神经元个数,l表示输出层节点的个数。基本BP神经网络包括信号的前向传播和误差的反向传播2个过程[20,21],即计算误差输出时按从输入到输出的方向进行,而调整权值和阈值则从输出到输入的方向进行。BP神经网络的学习通常使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络输出与期望输出的均方差最小。由于BP神经网络初始权值和阈值的随机性导致了训练次数增加,收敛速度较慢,且容易陷入局部最优。因此,本文将改进蛇优化算法与BP神经网络结合起来,利用蛇优化算法全局搜索性能强的优点来优化BP神经网络的初始权值和阈值。 以基于混合策略改进的蛇优化SSO算法获得BP神经网络的初始权值和阈值,然后使用BP反向传播算法训练神经网络,由此所得网络称为基于混合策略改进蛇优化算法的神经网络,记为SSO-BP神经网络。 SSO-BP神经网络分为2个部分:改进蛇优化SSO算法优化部分和BP神经网络部分。 改进蛇优化SSO算法优化部分负责产生BP神经网络的初始权值和阈值,它的目标是最小化期望输出与预测输出的均方差,具体目标函数表达式如下: (23) V=(v11,v12,…,v1q,v21,…,v2q,…,vd1,…,vdq) (24) W=(w11,w12,…,w1l,w21,…,w2l,…,wq1,…,wql) (25) θ=(θ1,θ2,…,θq),δ=(δ1,δ2,…,δl) (26) Bk=g(yk+δk) (k=1,2,…,l) (27) (28) Ac=f(bc+θc) (c=1,2,…,q) (29) (30) 其中,f(x)为隐含层激活函数,g(x)为输出层激活函数,Bk表示输出层的输出,dk表示期望输出,V和W表示权值向量,θ和δ表示阈值向量。 BP神经网络部分是以算法SSO优化得到的初始权值和阈值,利用训练数据进行训练,直至满足精度要求。 本文以红酒数据集和鲍鱼数据集为例,验证基于改进蛇优化算法的神经网络SSO-BP的性能。红酒数据集共有178组数据,每组数据由13个红酒特征与1个红酒所属类别组成,红酒所属类别是由红酒的13个特征所决定;鲍鱼数据集共有4 178组数据,每组数据由8个鲍鱼特征和1个鲍鱼年龄组成,鲍鱼的8个特征决定鲍鱼的年龄。以红酒数据集和鲍鱼数据集中前80%的数据作为训练数据分别训练SSO-BP神经网络、SO-BP神经网络、GA-BP(Genetic Algorithm-Back Propagation)神经网络以及基本BP神经网络,剩余数据作为测试数据测试4种网络的性能。4种网络的隐含层和输出层激活函数均使用Tansig函数和Purelin函数,算法SSO、SO和GA的种群规模均为30,迭代最大次数均为500,GA的交叉概率和变异概率分别为0.4和0.05,BP网络的最大训练次数均为200,学习率取0.1,训练精度为1E-5。训练完成后,比较4种网络对测试数据预测输出与期望输出的均方差以验证各种神经网络的性能。为避免偶然性,每种神经网络各自独立训练20次,并计算每次所得神经网络对测试数据预测输出与期望输出的均方差。取每种神经网络20次所得均方差的最好值、最差值、平均值及标准差进行比较,结果如表5和表6所示。 Table 5 Mean square error results of four neural networks for classifying red wine dataset Table 6 Mean square error results of four neural networks for predicting abalone dataset 由表5可知,SSO-BP神经网络对红酒进行分类的准确性和稳定性均比SO-BP神经网络、GA-BP神经网络和BP神经网络高。表6结果显示,用SSO-BP神经网络和GA-BP神经网络根据鲍鱼特征对鲍鱼年龄预测的准确性要比用SO-BP神经网络和BP神经网络预测的准确性高。综上,相比于对比的3种神经网络,基于改进蛇优化算法的BP神经网络SSO-BP具有更好的预测准确性和稳定性。 针对基本蛇优化算法容易过早收敛和陷入局部最优等不足,本文将维度选择策略、选择交配策略和重新分组策略引入基本蛇优化算法中得到了基于混合策略改进的蛇优化SSO算法。将维度选择策略引入基本蛇优化算法的战斗或交配阶段,从而有效避免算法迭代后期出现个体位置停滞现象。选择交配策略加强了迭代后期算法的探索能力,可以有效避免算法陷入局部最优。重新分组策略增加了种群多样性,提高了算法的寻优能力。30个标准测试问题的数值实验结果表明,与基本蛇优化SO算法及其他对比算法相比,基于混合策略改进的蛇优化SSO算法所得目标函数值与其理论最优值相差最小;相比基本蛇优化SO算法,SSO算法在求解高维无约束优化问题更具优势。统计学检验的结果表明,SSO算法求解大部分标准测试问题所得目标函数值明显好于SO算法所得的相应结果。仿真实验表明,相比其他3种网络,基于改进蛇优化算法的BP神经网络在分类红酒数据集和预测鲍鱼年龄时准确性和稳定性更高。但是,对于一些复杂优化问题,基于混合策略改进的蛇优化SSO算法求解所得目标函数值与理论最优值相差还是很大,未来需要进一步提高。
3 基于混合策略改进的蛇优化算法
3.1 维度选择策略
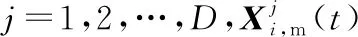
3.2 选择交配策略
3.3 重新分组策略
3.4 改进蛇优化算法的迭代步骤
4 数值实验
4.1 标准测试问题和数值结果对比


4.2 伸缩性检验
4.3 Wilcoxon秩和非参数检验
5 基于改进蛇优化算法的BP神经网络
5.1 基本BP神经网络
5.2 基于改进蛇优化算法的BP神经网络
5.3 实验结果与分析

6 结束语
