越野式伸缩臂叉装车整机稳定性理论计算方法和试验验证
2024-04-23苏宗洁党伟李海杰
苏宗洁 党伟 李海杰
摘 要:结合越野式伸缩臂叉装车国标GBT 26949.14-2016,通过受力分析及力矩平衡计算,结合稳定区域分析,得出了越野式伸缩臂叉装车稳定性计算分析的理论计算方法。通过试验验证了理论计算的可靠性,为伸缩臂叉装车的稳定性设计提供依据。在产品开发设计伊始就可以初估虚拟样机的稳定性能,降低了样机设计制造和试验的风险。
关键词:伸缩臂叉装车 稳定性 试验验证
1 引言
越野式伸缩臂叉装车是一种使用伸缩臂及安装在臂端的属具作为工作装置,集合了伸缩臂起重机、叉车、装载机等产品的特点,可进行搬运、铲装、吊载等多种作业,同时可有两轮转向、四轮转向、蟹行行驶等多种行驶模式,适应于多种地面状态的移动作业设备。
伸缩臂叉装车的整机稳定性,是指设备在行驶、作业过程中,整机抗倾覆的能力。在行驶及作业时,地面平整度及车辆状态可能会对整机稳定性有较大影响,都会影响最终产品的安全性和使用性。在设计初期就采用合适的方法对整车的倾翻稳定性情况进行计算,能最大限度的降低试验风险,而根据试验结果优化后的试验模型,也为后续的设计提供了参考依据。
2 稳定性性分析依据
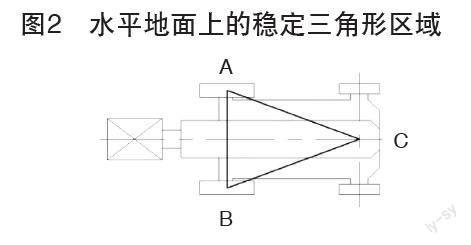
在作业时,伸缩臂叉装车可以根据不同工况需求,使用轮胎或稳定器作为接地支撑,稳定器一般布置在前桥前方,可以提高前方和侧方的作业区域。同时为了提高越野能力,后桥多采用摆动式。因此在计算稳定性时,倾翻线围成的稳定区域为图2所示的三角形ABC区域。
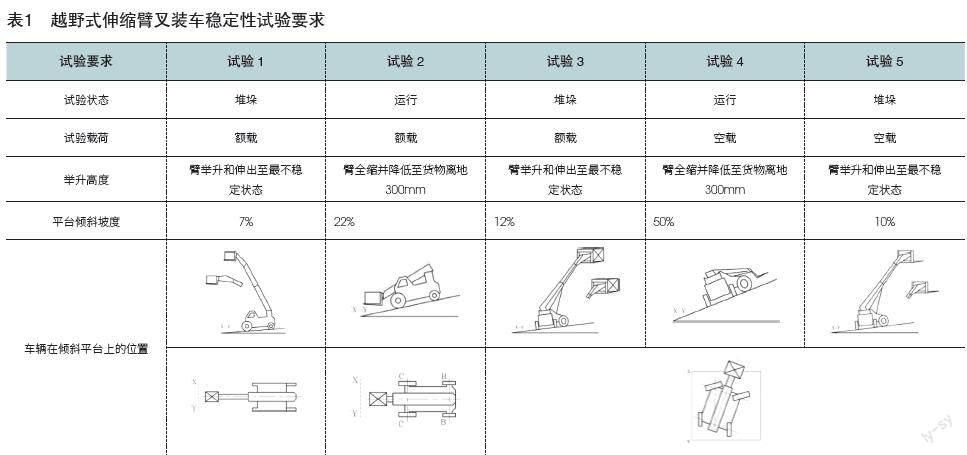
针对整车稳定性的,目前国标、ISO标准和欧洲标准及美标中都是采用模拟表1中几种典型工况的试验方式来验证。根据国标GBT 26949.14-2016要求,稳定性验证需要通过五个测试,其中,试验1主要验证在不同臂长和臂仰角的带载工况下,整机的纵向稳定性。
试验2为模拟车辆在货物放低,轮胎行驶情况下纵向倾翻稳定性极限工况。试验3为验证在不同臂长和臂仰角的带载工况下,车辆侧后方倾翻线的稳定性。试验4为验证空载、臂架收回状态下,车辆在侧后方倾翻线的整机稳定性。试验5是验证空载、臂架最大仰角下全伸到全缩状态的整车在侧后方倾翻线的稳定性,这个状态下,因为后方倾翻线围成的区域较窄,同时臂的抬升会导致重心向侧后方向移动,也容易产生整机侧后方的倾翻。
上述试验中,试验1和试验3共同决定了整机的稳定性起重量,试验2、4、5验证了典型工况下的整机稳定性能力。
目前车辆上的稳定性检测设备及方法主要有两种,一种是采用在后桥安装应变检测仪,实时检测后桥承载的变化,通过与预先设定的允许值对比,判断整机是否处于所允许的稳定工作状态。另一种方法为采用力矩限制系统,通过检测压力、臂长、臂仰角,计算出当前载荷状态,通过与设定的理论允许状态的比对,来检测是否整机处于稳定状态,第二种方法更适用于上装可以相对底盘回转作业的机型。此处设计的方法和试验是以第一种后桥采用应变检测仪的设备为例。
在各种试验工况中,由于处于倾斜的台面上,实际的倾翻线围成的区域应该是理论稳定三角形在地面的投影abc(图3)。
伸缩臂叉装车的稳定状态的性能就以在上述试验工况,后桥还有一定地面的支撑反力作为余量的前提下,整机重心保持在上述的稳定三角形投影区域范围内时设备的理论提升能力来计。整机稳定性的极限时的状态即地面对后桥的支撑反力为零,但设备和重物合计的重心仍落在稳定三角形区域内。
3 稳定性分析方法
以倾翻线为基准,根据标准要求的不同工况下,倾翻力矩和稳定性力矩平衡,计算得到叉装车的理论稳定性起重能力;
例如,试验2中正前方以前桥在地面投影为倾翻线,在水平地面状态下计算倾翻极限,可列方程如下:
Q×L2=G×L1-F×L3
Q:提升重物的质量;G:伸缩臂叉装车自重;F:后桥支撑反力;L1:伸缩臂叉装车重心到前桥轴心的水平距离;L2:提升重物的质心到前桥轴心的水平距离;L3:前后轴距;H1:提升重物的质心到地面的垂直距离;H2:伸缩臂叉装车的重心到地面的垂直距离。
如果换到倾斜面上,可列力矩平衡方程如下:
Q×(L2*cosα+H1*sinα)=G×(L1*cosα-H2*sinα)-F×L3*cosα
Q:提升重物的质量;G:伸缩臂叉装车自重;F:后桥支撑反力;L1':伸缩臂叉装车重心到前桥轴心的水平距离;L2':提升重物的质心到前桥轴心的水平距离;L3':前后轴距;H1:提升重物的质心到地面的垂直距离;H2:伸缩臂叉装车的重心到地面的垂直距离。
据此可以求得各个臂长、仰角状态下前方满足稳定性的最大起重量Q。
试验3、试验4和试验5主要为验证整机侧后方稳定性情况,因伸缩臂叉装车的后桥为摆动桥,因此整车的倾翻线为以后桥轴心和纵向中心面交点在地面的投影,与两个前轮中心在地面的投影连线做倾翻线。计算原理与试验2类似,此处不再赘述。
通过力矩平衡可以求出满足单个试验条件下整机稳定性能,同时满足试验1到试验5的前提下,即可得到整机的理论稳定性能和稳定性作业范围;
初步定义该伸缩臂叉装车的额定起重量为3吨,最大工作仰角为73°,最大起升高度為13.5米,三维设计过程中,通过三维建模估算整机的重量和重心,并进一步计算,可得到试验1和试验3整机在不同角度和臂长下的起重能力,如表2、表3。
试验2、试验4、试验5通过计算也能满足设计定义的仰角和起升高度范围。
4 试验验证及校准
在标准的要求设定的试验条件下,先在平面状态的倾翻试验台上,按理论计算的起重量和臂长、臂仰角状态停放车辆,再操作翻转试验台,确认整机稳定情况,并记录。试验过程中通过调整吊臂仰角,尽量找到整机的稳定性极限状态。试验中要做好保护,防止整机倾翻。
经对理论计算的工况进行重物提升试验,结果发现:
实测吊臂稳定性极限角度和理论对比都有范围在±5°左右的偏差,试验1中,较长的臂长和较大的起重量的工况下,理论和实侧的值偏差相对更大;
试验中测试的轮胎支撑的工况相对于支腿支撑的工况,实侧值和理论对比差距更大。在轮胎支撑时,带载后,因为重心偏离车辆的纵向或横向中心,会导致重心偏向侧的轮胎受压较大,产生更大的变形,轮胎的不同变形量导致车辆相对水平地面产生额外的倾斜角度,也会影响整机的稳定性起升性能。在后续的计算模型中,考虑了轮胎变形对整机姿态的影响,进行了计算矫正。
在大臂伸出较长的情况下,臂会产生一定的下挠量,也可能会对稳定性造成不良影响,在后续的理论计算中,增加了相关的影响系数,以减少理论计算和实际测试的差距。测试样机的调试过程中,也需采取一定的措施来控制变形量以降低对设备实际起升能力的影响。
5 结论
通过以上稳定性理论计算方法,计算出伸缩臂叉装车的理论载荷性能表,再通过试验验证和结果对比分析,对计算模型不断优化矫正,最终可以建立一套贴近实际试验工况的计算方法;可在此理论基础上结合程序设计,快速生成理论的作业载荷性能表和初步的作业载荷分布图,并对后续产品的研发提供计算依据和指导参照。
参考文献:
[1]闰洪峰.TH4013SL型伸缩臂叉装车的结构设计与试验分析[D].2008-7.
[2]曾立斌,侯忠明.伸缩臂叉装车发展概述[J].物流技术,2000(02):13-14.
[3]侯忠明,胡彝.某型伸缩臂叉车稳定性验算[J].起重运输机械,2010(02):28-30.
[4]田甜,陈宇,刘学文,郑艳超.伸缩臂叉装车作业稳定性分析[J].时代汽车,2018(08):105-106.
