采用联合算法识别人-桥耦合系统时变模态参数

方露，彭佳敏

（福建农林大学交通与土木工程学院，福州 350002）

0 引言

在人致激励下，人行桥的频率和阻尼比不可避免地会发生变化[1]，这使得其在服役过程中存在严重的安全隐患。为监控服役期间人行桥的安全状态，需对其频率和阻尼比进行识别。获得自由衰减振动信号是识别人行桥时变模态参数的首要工作。当人行桥受到近似周期性激励时，其响应信号由强迫振动分量和自由衰减振动分量两个部分构成[2]。因此，通过解析模态分解（Analytical Mode Decomposition,AMD）[3]等分解方法可以获取自由衰减振动信号[4]。然而，受测量方法和噪声的影响，自由衰减振动信号的获取结果可能存在失真情况，这导致阻尼诊断结果相对频率的识别结果而言偏差较大[5]。为此，本文引入差分自回归移动平均模型（Autoregressive Integrated Moving Average Model, ARIMA）[6]对失真处的信号进行预测。目前，基于自由衰减振动信号识别结构时变阻尼比的主要方法有连续小波变换（Continuous Wavelet Transform,CWT）[7]和同步挤压小波变换（Synchrosqueezing Wavelet Transform,SWT）[8]等。然而，CWT在低频信号的处理过程中频率分辨率较低[9]，从而降低了阻尼比识别结果的精度。虽然SWT通过同步挤压操作可以提高频率分辨率，但也会造成对数形式的SWT系数模值曲线产生不平稳现象，从而影响了阻尼比的识别效果。作为一种新的瞬时频率识别方法，多重同步提取变换（Multi-Synchrosqueezing Extracting Transform, MSSET）[10]不仅拥有较高的时频分辨率，而且具有稳定的时频系数模值。因此，本文基于AMD、ARIMA和MSSET算法提出了一种识别人-桥耦合系统时变模态参数的联合方法。通过人桥耦合数值算例和华威人行试验桥对所提方法进行了验证。研究表明：联合方法可以有效解决多种因素下自由衰减振动信号提取结果不准确的问题。此外，该方法识别的瞬时频率和时变阻尼比曲线可以清晰地表征行人空间位置变化对钢-混组合人行桥频率和阻尼比的变化趋势。

1 联合方法

联合方法结合了AMD、ARIMA和MSSET等算法。首先，通过AMD从人-桥耦合系统响应信号中分解出人行桥在人行荷载激励下被激发的模态分量信号。当人行桥作受迫振动时，AMD分解获得的模态分量信号即为自由衰减振动分量信号。然后，根据时频方法识别的瞬时频率和对数时频系数模值曲线的结果，判断并舍弃自由衰减振动信号中失真的部分。在此之后，采用ARIMA预测该失真部分的信号。最后，结合MSSET识别第一阶竖向模态振型分量信号和自由衰减振动信号的MSSET系数及瞬时频率，再将MSSET系数模值以对数的形式表示并推导瞬时频率、MSSET系数模值与阻尼比三者之间的函数关系，从而最终估算出系统的时变阻尼比。其中，有关AMD、ARIMA和MSSET的详细内容可参考文献[3]、[6]和[10]，在此不再赘述。本文主要阐述瞬时频率、MSSET系数模值与阻尼比三者之间函数关系的推导过程。

在t时刻有阻尼的单自由度振动系统的自由衰减振动幅值信号为XA（t）=Aef0 t，（f0=－ξωn），将XA（t）经过MSSET后得到的MSSET系数如式（1）所示：

式中，g赞ω（·）为紧支高斯窗函数gω（·）的傅里叶变换。

由于MSSET提取的结果为瞬时频带而非时频脊线，因此，本文引入模极大值法求取MSSET的时频脊线，如式（2）所示：

式中，k为时频图中频率轴的最大值，c为MSSET系数矩阵的维数，P（t，η）为TMSSET（t，η）的模极大值。

在得到MSSET系数和瞬时频率之后，人-桥耦合系统时变阻尼比的具体估算过程如下。

在式（1）中，当ω=f0时，g赞（ω－f0）=1。此时，可得

将式（3）左右两边先同时取绝对值，再将其结果以对数形式表示，如式（4）所示：

式（4）两边同时对时间t求导，可得时频系数、瞬时频率和阻尼比之间的函数关系，如式（5）所示：

式中，ωMSSET为人-桥耦合系统的瞬时圆频率。

2 数值算例验证

2.1 人-桥耦合有限元模型的建立

2.1.1 连续步行荷载模型

本文采用傅里叶级数表示具有近似周期性的连续步行荷载模型[11]。为符合我国国民的体质，本文行人模型的体重和步频参数根据文献[12]分别选取626.34 N和1.77 Hz。最终模拟的连续步行激励荷载曲线如图1所示。根据参考文献[11]，人行桥上所施加的连续步行激励如式（6）和图2所示。

图1 连续步行激励荷载曲线

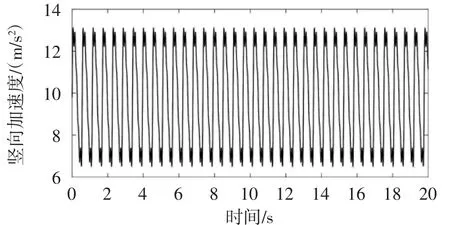
图2 连续步行激励竖向加速度曲线

式中：Fh为连续步行荷载，N；W为行人体重，N；g为重力加速度。

2.1.2 人-桥耦合模型

通过ABAQUS建立连续钢-混凝土组合人行桥模型，如图3所示。该人行桥总跨长为16 m，共两跨，每跨8 m，桥面净宽为1.6 m，板内布置双层钢筋网，布置情况均为ϕ8@200 mm。人行桥中的主梁和横梁均采用H型钢梁。钢筋和混凝土面板的弹性模量E和泊松比等材料参数如表1所示。

表1 钢筋混凝土面板材料参数

图3 钢-混组合人行桥有限元模型

通过ABAQUS计算获得人行桥的一阶和二阶竖向弯曲模态频率分别为9.816 Hz。根据规范ISO 10137，将钢-混组合人行桥模型的阻尼比设定为0.6%[13]。

在人-桥耦合系统中，行人应作为一个独立的动力系统依附在人行桥上。根据文献[14]，本文通过弹簧阻尼器连接两个不同的质量块建立SMD人体模型。行人模型的刚度设为14.11 kN/m，阻尼比为0.3[15]。将质量块与桥面之间的摩擦因数设为0。为防止行人模型行进时发生穿刺现象，将行人模型与桥面的法向属性定义为硬接触以此实现人桥耦合，如图4所示。然后，设定人体模型以1 m/s沿纵桥方向匀速行进，将隐式动力分析步中默认施加的重力加速度替换为式（6）中的竖向加速度Ah。

图4 人-桥耦合有限元模型

2.2 数值算例结果

设定分析步时间间隔为2 ms，对组合人行桥进行隐式动力分析，提取钢-混组合人行桥左侧跨中的加速度响应信号，如图5所示。从图5可以观察到行人刚进入人行桥时产生了较大的冲击，然后随着行人的行进响应逐渐增大，当行至跨中位置时达到顶峰，随后逐渐减小。对钢-混组合人行桥响应信号进行快速傅里叶变换，结果如图6所示。在图6中，0～9 Hz范围内的5个分量信号为5个强迫振动分量信号，而在9～12 Hz区域内出现的信号为人行桥一阶竖向弯曲模态振型的分量信号。根据文献[2]、[4]可知该信号也为自由衰减振动分量信号（图6中方框）。选取截止频率为9.6 Hz和13 Hz，采用AMD分解获得的自由衰减振动分量信号如图7所示。

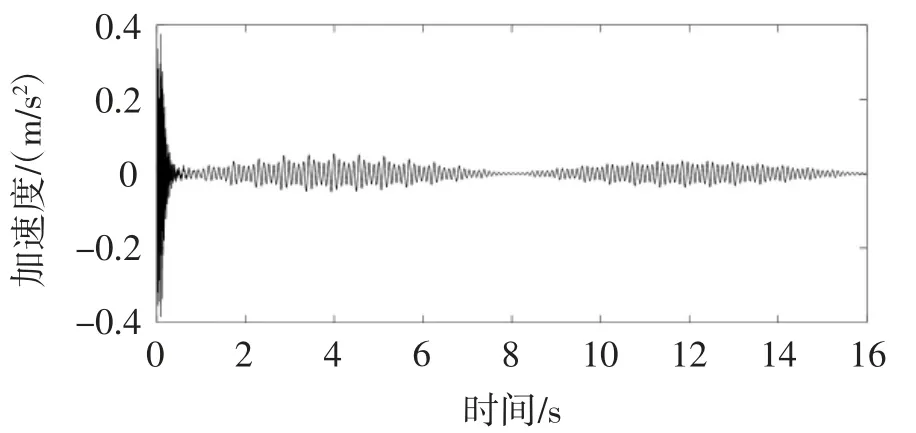
图5 钢-混组合人行桥响应信号

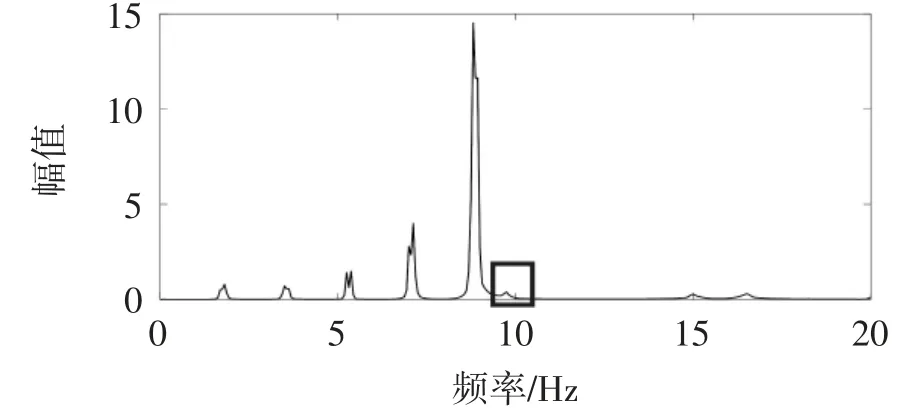
图6 钢-混组合人行桥响应信号FFT幅值图

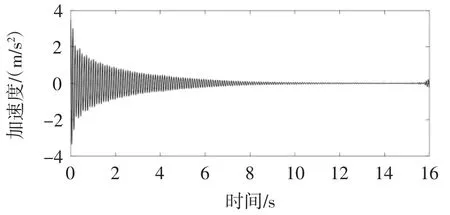
图7 AMD分解获得的自由衰减振动响应信号

通过观察图7可知：在14～16 s区域，自由衰减振动响应信号并未较好地呈现出递减的现象，其原因是受到了提取方法的限制以及结构阻尼衰减的影响。为解决此问题，本文采用ARIMA对14～16 s区域的信号进行预测，其最终得到的预测模型为ARIMA（19, 0, 0），预测的自由衰减振动分量信号如图8所示。通过对比图7和8可知：图8在14～16 s区域中信号衰减的现象更为明显。

图8 预测后钢-混组合人行桥自由衰减振动响应信号

采用附加移动质量法获得人行桥固有频率理论值[11]，设定每次移动的距离为1000 mm，最终得到图9和10中黑色实线所示的理论固有频率曲线。将AMD分解出的自由衰减振动信号和预测后的自由衰减振动信号分别进行CWT、SWT、SET和MSSET处理得到系统的瞬时频率曲线，如图9和10所示。从图9可知：CWT（十字实线）和SWT（菱形点线）识别的瞬时频率曲线无法反映人行桥在服役状态下的时变特性，而SET（菱形虚线）和MSSET（圆形虚线）识别的结果可以很好地表现出时变特性，其中MSSET的效果最佳（图9矩形框）。对比图9与10可知：图10在14～16 s区域中各算法识别的频率结果与理论值更为吻合（图10矩形框所示）。

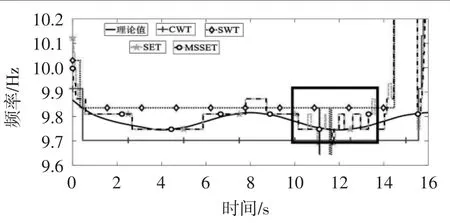
图9 预测前钢-混组合人行桥瞬时频率

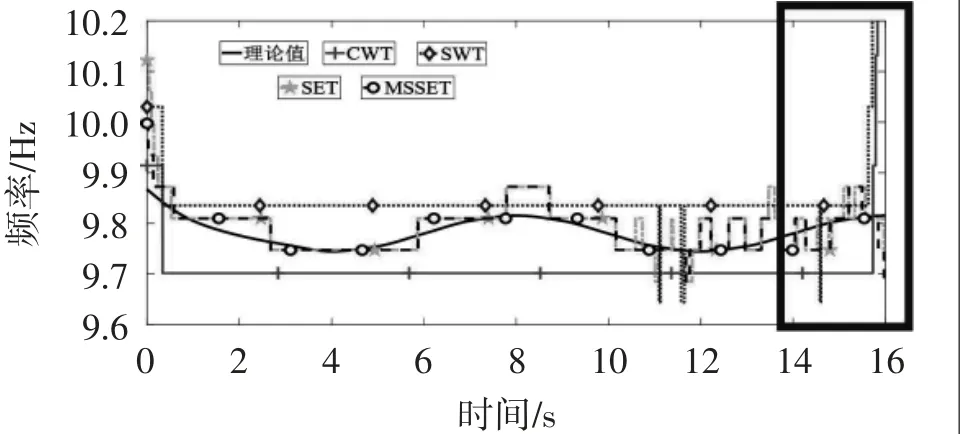
图10 预测后钢-混组合人行桥瞬时频率

对AMD分解获得的自由衰减振动信号及其预测后信号分别进行CWT、SWT、SET和MSSET处理，提取各算法时频系数模值并以对数形式表示，如图11和图12所示。在图11和图12中，除了在14～16 s区域外，相比SWT，CWT、SET和MSSET均较好地保持了对数时频系数模值的稳定性。然后，通过线性最小二乘拟合对数时频系数模值曲线，如图11和图12中虚线所示。

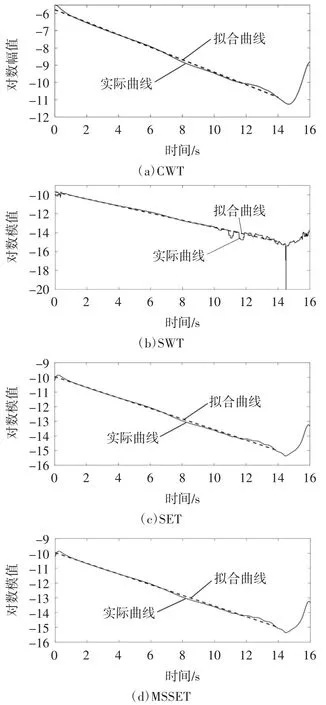
图11 预测前时频系数对数模值图及其拟合曲线

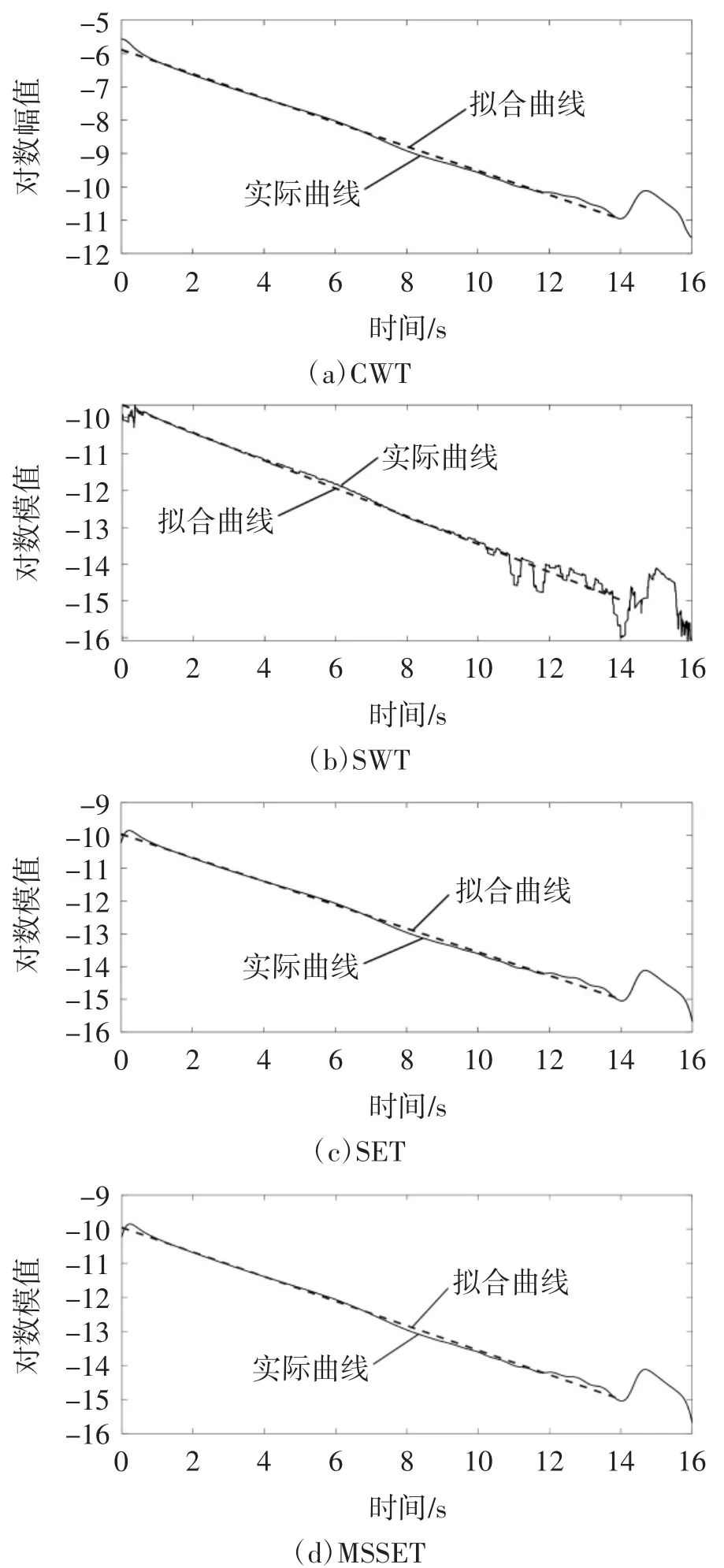
图12 预测后时频系数对数模值图及其拟合曲线

在获取各算法识别的瞬时频率和对数时频系数模值之后，根据式（5）估算人-桥耦合系统的时变阻尼比，如图13和14所示。从图13和图14可以得知：除14～16 s之外的时间范围内，MSSET和SET的识别结果精度高于CWT和SWT的识别结果，即MSSET和SET的识别结果与理论阻尼比值（理论阻尼比值为0.6%）更为接近，其中MSSET的识别结果略高于SET的识别结果（图13矩形框所示）。此外，从图13和14可以观察到：行人在行进时，阻尼比在逐渐增大。当行人行至各跨跨中时，阻尼比值达到峰值，随后又在逐渐减小。通过对比图13与图14可知：图14在14～16 s区域中各算法识别的时变阻尼比结果与理论值更为吻合（图14矩形框所示）。

图13 预测前钢-混组合人行桥时变阻尼比

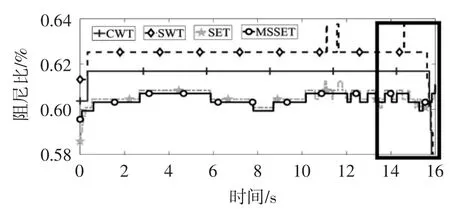
图14 预测后钢-混组合人行桥时变阻尼比

3 试验验证

在本节中，采用文献[16]提供的华威桥试验数据来证明联合方法的有效性。华威桥是单跨钢-混组合人行桥，全长19.9 m，桥体由混凝土面板和两根H型钢梁组成。该桥在一阶竖向弯曲模态振型下的频率为2.4 Hz，模态阻尼比为0.3%[16]。试验时，测试者在华威桥上近似匀速行走，使其位置随时间而变化，从而实现了人-桥耦合系统的时变特性。此次试验采用QA加速度传感器和NI9234采集卡获取步行激励下人行桥垂直方向的加速度，采样频率为100 Hz。

本文截取测试者返程时走过全桥的加速度信号，时长约为11 s，如图15所示。从图15可知：当行人逐渐行至跨中时，华威桥的响应逐渐增大并在跨中位置达至顶峰，随后逐渐减小。将其响应信号经过CWT处理得到图16所示的小波量图，其中处于2 Hz的分量信号为激励信号，2.4 Hz的分量信号为人行桥受步行激励而产生的一阶竖向弯曲模态信号。

图15 华威桥响应信号

图16 华威桥响应信号小波量图

选取AMD的截止频率分别为2.2 Hz和4.0 Hz，从华威桥响应信号中分解出图16中2.4 Hz处的分量信号。将分解出的信号经过CWT、SWT、SET和MSSET处理后得到该信号的瞬时频率，如图17所示，其中，黑色实线是根据文献[11]求得的公式值。从图17可以看出：相比于其他3种方法，MSSET不仅能够更稳定地反映出频率随行人空间位置发生的变化趋势，而且具有更高的时频分辨率。

图17 华威桥瞬时频率识别结果图

文献[16]采集的自由衰减振动信号如图18所示。类似地，分别采用CWT、SWT、SET和MSSET处理自由衰减振动信号得到各算法时频系数的对数模值，通过最小二乘拟合各对数模值曲线得到各曲线的斜率，如图19虚线所示。

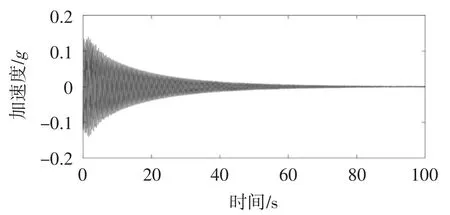
图18 预测前华威桥自由衰减振动响应信号

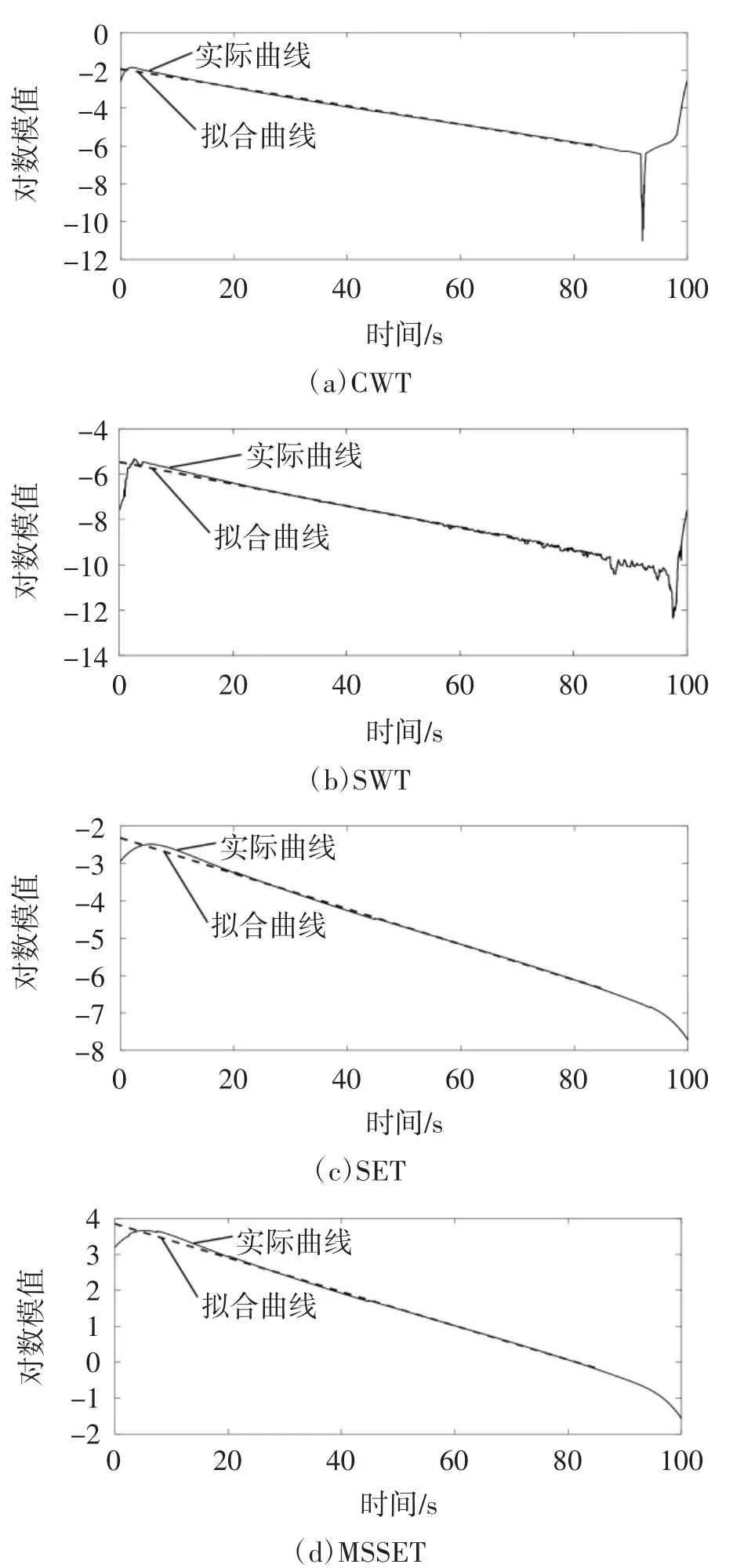
图19 预测前华威桥时频系数对数模值曲线图及其拟合曲线

由于自由衰减振动信号末端的能量相对较小，因而容易被噪声淹没并产生一定的误差，这导致CWT对数模值曲线在尾部失真。为改善此问题，通过ARIMA对85～100 s的自由衰减振动信号（如图20）进行预测，经计算，其预测模型为ARIMA（19, 0, 7），失真区域信号的预测结果如图21所示。对比图20和图21可知，经预测后的信号曲线更光滑，信号幅值递减趋势更显著。为更好地表征目标信号，图22给出了0～100 s的预测自由衰减振动信号。

图20 预测前85～100 s华威桥自由衰减振动响应信号

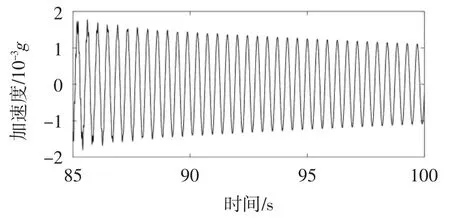
图21 预测后85～100 s华威桥自由衰减振动响应信号

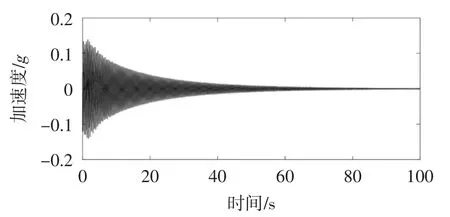
图22 预测后华威桥自由衰减振动响应信号

类似地，将预测后的信号分别进行CWT、SWT、SET和MSSET处理，得到其时频系数模值并以对数表示，结果如图23所示。通过对比图19（a）、（b）和图23（a）、（b）图可以观察到：CWT和SWT处理预测后信号所得到的时频系数对数模值曲线比未预测的结果更加理想，递减的趋势更趋于稳定。然后，通过线性最小二乘拟合得到各算法对数模值曲线的斜率值，如图23虚线所示。

图23 预测后华威桥时频系数对数模值曲线图及其拟合曲线

根据式（5）估算华威桥时变阻尼比，结果如图24和图25所示。从图24和图25可知：人行桥在服役期间，其阻尼比将随行人空间位置变化而变化；相比于其他算法，MSSET的识别结果更能清晰稳定地体现出人行桥的时变模态参数随行人空间变化而引起的变化趋势。通过对比图24和图25可知：ARIMA可以显著地改善CWT和SWT算法的阻尼比识别效果。因此，本文提出的方法不仅可以较好地解决提取自由衰减振动信号中尾部信号不够精确的问题，而且基于该方法识别的时变模态参数具有更高的精确度。

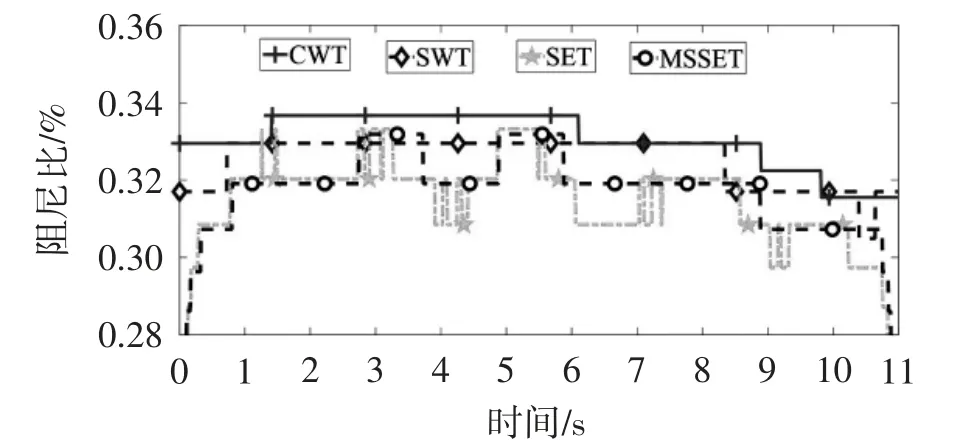
图24 预测前华威桥时变阻尼比曲线图

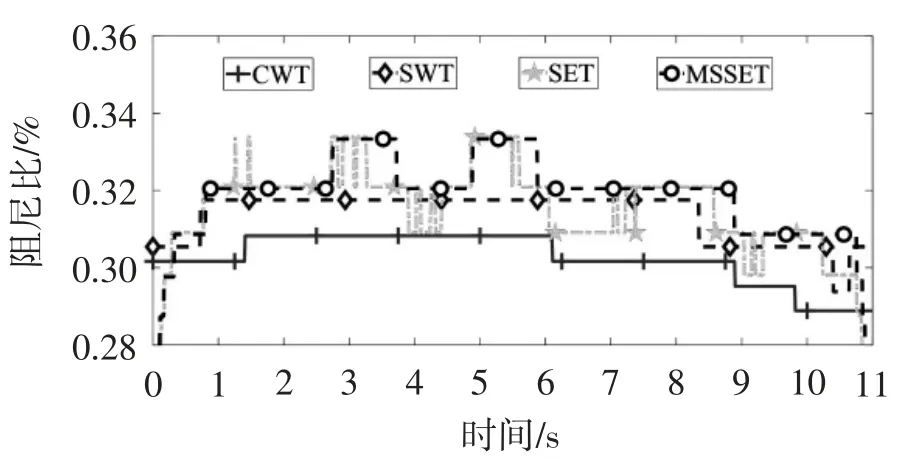
图25 预测后华威桥时变阻尼比曲线图

4 结语

为更加准确地识别服役状态下钢-混组合人行桥的时变模态参数，本文从人-结构相互作用的角度出发，提出了一种基于AMD、ARIMA和MSSET等算法的人-桥耦合系统时变模态参数联合算法。最后，通过数值算例和步行试验对文中方法的有效性和准确性进行了验证。研究结果表明：联合方法可以有效解决自由衰减振动信号提取结果不准确的问题，并且该方法识别的瞬时频率和时变阻尼比曲线可以清晰地表征行人空间位置变化对钢-混组合人行桥频率和阻尼比的变化趋势。