混合整数优化问题的差分进化算法研究

李道军，李廷锋，卢青波

（郑州职业技术学院，郑州 450121）

0 引言

在机械优化设计问题中，经常会遇到混合整数优化问题，即在数学模型中同时存在连续设计变量和整型设计变量，例如：在设计圆柱齿轮减速器时，齿轮的齿数是整型设计变量，减速箱的宽度则是连续变量。这类问题在机械工程领域非常普遍，因此对于混合整数优化问题的求解技术研究具有普遍的工程意义。

混合整数优化问题的数学模型一般表示为：

对于上述模型，当p=0时为一般的连续变量问题，当p=D时为整数规划问题，其余情况为混合整数优化问题。

针对混合离散性优化问题，陈立周[1]给出了一些颇为实用的求解方法。Appa等[2]对混合离散优化问题的求解方法进行了总结。连青惠等[3]对非均匀离散变量及连续变量的均匀离散化方法进行了说明，分析了求解混合离散变量优化问题的一般方法。轩华等[4]提出了混合离散变量优化的灰色混沌复合遗传算法。Sun等[5]基于可行规则提出了求解混合离散变量问题的改进粒子群算法。文献[6]～[11]提出了求解非线性混合整数非线性规划问题的改进差分进化算法。车林仙等[12]提出了面向工程约束优化的混合离散差分进化算法。

以上研究利用不同的方法对混合离散性优化问题的求解技术进行了研究。其中，文献[6]～[12]是基于差分进化算法的研究，这些研究采用不同方法将差分进化算法应用到混合整数非线性优化问题的求解中，但都未结合差分进化算法特点为混合整数优化问题设计通用的求解方法。本文将针对整数变量的特点，从差分进化算法的变异算子入手，研究提出能够单独处理整数变量的变异算子，使差分进化算法能够直接对整数变量进化，进而提出混合整数优化问题的差分进化算法，并与已有几种改进算法进行对比研究，验证所提出方法的有效性。

1 基本差分进化算法

差分进化算法[13]的每个个体用一个实向量来表示，初始种群采用均匀分布的随机数生成。令xi（g）代表第g代的第i个个体，则有

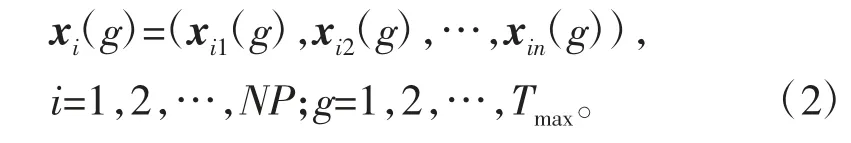
差分进化算法的进化过程如下所述。

1）初始化种群。在n维实数空间按式（3）随机产生NP个个体：

式中，rand（0，1）为［0，1］上服从均匀分布的随机数。

2）变异算子。变异算子是差分进化算法的关键步骤，其过程为从当前种群中随机选择3个不同个体xp1、xp2、xp3，且p1≠p2≠p3≠i，则有

式中，F为缩放因子。

3）交叉算子。交叉算子可增加种群的多样性，其过程如式（5）所示：

式中：CR为交叉概率，CR∈［0，1］；jrand为［1，n］的随机整数，这种交叉模式确保vij（g+1）中至少有1位来自hij（g）。

4）选择算子。差分进化算法采用的是“贪婪”选择策略，由评价函数对向量vi（g+1）和向量xi（g）进行比较，获胜者保留。计算公式为：

反复执行式（4）～式（6），直到达到算法预设的终止条件。

2 混合整数差分进化算法

差分进化算法的变异算子对候选解的产生起到至关重要的作用。对于混合整数问题，如何实现整数变量的进化成为算法求解该类问题的关键。因此，本文针对整数类型变量设计专用的变异算子，以使整数变量能够直接参与进化。

2.1 整数变量的初始化

2.2 整数变量的变异算子

对于整数变量，为保证其变异后的结果仍为整数变量，这里首先对式（4）中的F约束为随机整数RandInt（0，Fmax）。其中Fmax为最大整数取值。其次，为保证随机性，对式（4）的求解结果进行处理，具体的处理过程如表1所示。

表1 算法1的均匀离散变量变异算子伪代码

2.3 灾变策略

采用差分进化算法时，随着进化代数的增加，群体的差异度缩小，尤其是在变量取值较少的情况下，这种缩小会很快，从而使群体陷入局部最优解。为减缓这种趋势，提升算法的全局搜索能力，引入灾变因子DF，对群体中的个体进行小概率淘汰，使群体中的个体在进化中以一定的概率淘汰。这样的操作保证了群体中有新个体的加入，达到提升群体多样性的目的，从而提升算法的全局搜索能力。本文设置当个体在选择操作后，若父代个体未更新且满足rand（0，1）＜DF，则对父代个体进行重新初始化。

2.4 混合整数差分进化算法流程

结合算法1与灾变操作，提出混合整数差分进化算法（Mixed-Integer Differential Evolution，MIDE）。其算法流程如下所示。

Step 1：初始化算法参数；

Step 2：对整数变量与连续变量分别在其定义域内随机初始化；

Step 3：对每个个体执行：

Step 3.1：变异操作，整数变量按算法1进行，连续变量按标准DE算法执行；

Step 3.2：交叉操作；

Step 3.3：选择操作，若个体未进行更新且满足rand（0，1）＜DF，对该个体初始化；

Step 4：判断是否达到收敛条件，否则转Step 3继续执行；

Step 5：输出结果。

3 仿真与分析

为检测MIDE算法的性能，设置种群大小为100，将整数变量变异算子中的缩放因子设置为RandInt（0，3），即取0～3中的随机整数，将连续变量的缩放因子设置为0.5，将交叉率设置为0.1，将灾变因子设置为0.01，每个问题独立运行50次。测试环境为：Intel CoreTMi5，8 GB RAM，Win7，VS2010。

本文采用Deb提出的可行规则方法[14]处理约束条件。

1）问题1。多项式优化问题：

式中：-10≤xi≤10，且xi为整数（i=1，2，…，7）。

该问题的最优解为x*=（2，2，0，4，0，1，2），函数最优值为f1（x）min=700。

2）问题2。Himielblau约束优化问题：

其中：

式中：78≤x1≤102，33≤x2≤45，27≤x3、x4、x5≤45，且所有变量取整数。

3）问题3。混合整数优化多项式问题：

该问题的全局最优解为：x*=（1，0，0，1，0.2，1.280624，1.954483），函数最优值为f3（x）min=3.557463。

文献[12]采用问题1与问题2测试HDDESPF算法处理整数规划问题的能力。文献[7]采用问题3测试算法处理混合整数优化问题的能力。本文采用以上3个问题测试所提出的MIDE算法的性能。

表2给出了MIDE算法进化500代的求解结果与其它算法的比较。从表2数据可以看出，MIDE算法与HDDESPF及DDESPF算法都能较好地求解该问题，但本文算法平均耗时最短。从图1的收敛曲线可以看出，MIDE算法在进化约125代（函数评价次数约为12 500次）后，获得最优值。

图1 MIDE算法求解f1（x）的收敛曲线

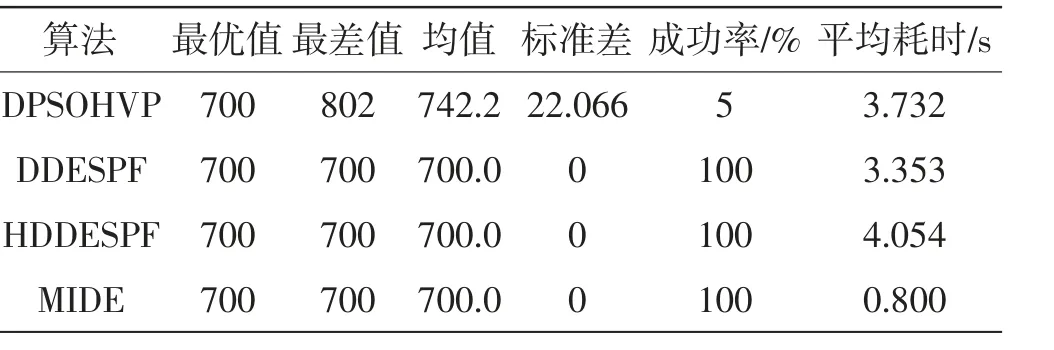
表2 4种算法求解f1（x）的统计结果比较

表3给出了4种算法求解问题2的统计结果比较。从表3中数据可以看出，MIDE算法获得了新的最优值，且能完全收敛到该新的最优解。图2为MIDE算法求解f2（x）时的收敛曲线。从图2中可以看出，MIDE算法在200代之前（即目标函数的评价次数为20 000次）获得了该问题的最优解。

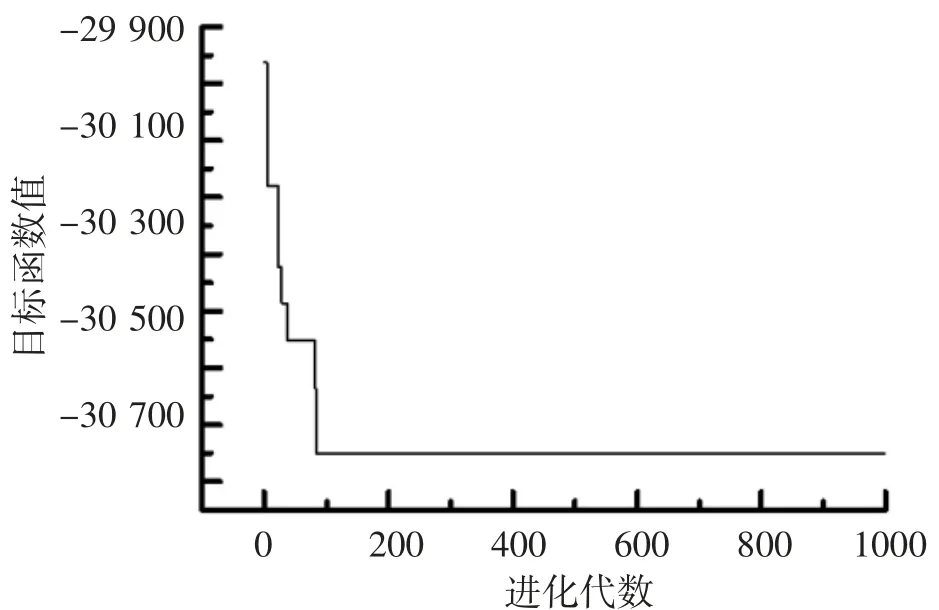
图2 MIDE算法求解f2（x）的收敛曲线

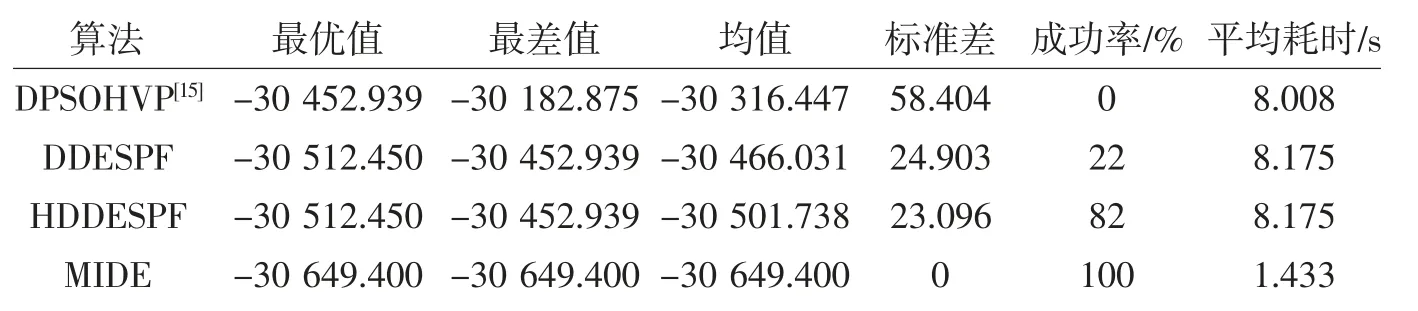
表3 4种算法求解f2（x）的统计结果比较

DDESPF与HDDESPF获得的f2（x）的最优解为：x*=（81，33，30，45，36），函数最优值为f2（x）min=-30512.45。MIDE算法进化1000代的最优解为x*=（78，33，30，45，37），函数最优值为f2（x）min=-30649.40。其中约束条件的值为：g1（x）=91.9929，g2（x）=98.8939，g3（x）=20.0333。该解为可行解。

表4给出了3种算法求解问题3的结果比较。其中，MIDE算法结果采用文献[7]中算法设置。从表4中数据可以看出，MIDE算法在相同设置下，获得的最优解要优于其余2种算法，且算法能稳定收敛。图3给出了3种算法求解f2（x）时的收敛曲线比较。从图3中可以看出，MIDE在进化400代左右收敛到最优点，其收敛速度要快于MIHDE与CLSDE算法。

图3 3种算法求解f3（x）的收敛曲线

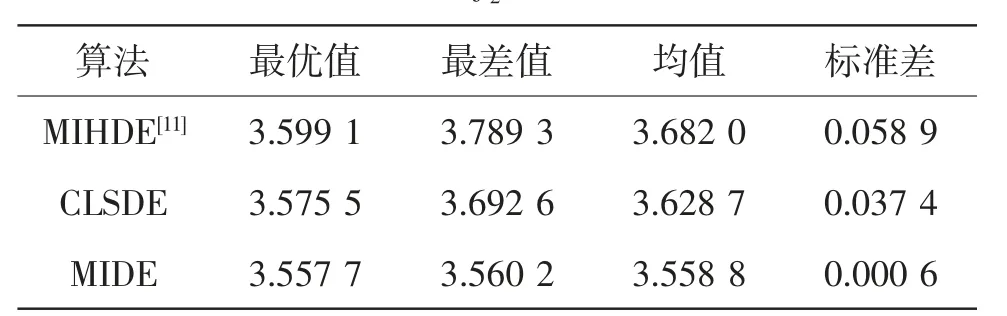
表4 3种算法求解f2（x）的统计结果比较

4 结论

本文结合混合整数优化问题的特点，为差分进化算法设计了整数变量的变异算子，进而提出了混合整数差分进化算法。与自适应罚函数混合离散差分进化算法（HDDESPF）及CLSDE算法进行了试验对比，结果表明：1）本文算法在运行时间上要优于HDDESPF算法，并在Himielblau约束优化问题上获取了比HDDESPF问题更优的最优解，且能稳定收敛到该最优解；2）在算法的收敛性及稳定性上要优于CLSDE算法；3）由于算法设计了整数变量的变异算子，使得进化直接在整数域内进行，因此比应用于整数规划优化问题求解更快，如背包问题。

MIDE的测试结果表明了其优化性能，下一步将研究其在更广泛领域（如0/1背包问题、旅行商问题、车间调度问题等）中的应用。