分解法设计计数器电路分析与仿真
2024-04-20马宏兴贾浩博刘旋丁雨恒
马宏兴,贾浩博,刘旋,丁雨恒
(北方民族大学 电气信息工程学院,宁夏银川,750021)
设计时序电路时,可以用编码器、译码器、数据选择器、加法器、计数器、寄存器等中小规模集成电路,外加门级电路如与、或、非及与非、或非等电路,完成相应功能。由于生活中需要各种计数功能,因此时序电路中最为常见的也是各种计数器的设计。
计数器是电路设计中使用最为广泛的时序逻辑电路,能够记忆脉冲个数。计数器设计原理是基于时序电路和触发器,通过触发器状态的改变实现数字的累加。计数器不但可以记数,而且还可以用于定时、分频、脉冲产生和数字运算。
1 计数器设计原理
设计计数器时,常采用现有的集成计数字电路来设计所指定的计数器。假定已有N进制计数器,需要设计M进制计数器,当设计的M进制计数器的M小于给定的N进制计数器时,只需要选取N 进制计数器中的M种状态即可;当设计的M进制计数器的M大于给定的N进制计数器的N时,须将多片N进制计数器级联,此时设计方法分为整体清零计数法和分解计数法。
(1)整体清零计数法
整体清零计数法的基本思想是先将n片计数器级联组成N n(Nn>m)进制计数器,在计满M个状态后,采用整体清零,使得计数状态在0~M- 1之间循环,从而实现M进制计数器。
(2)分解计数法
分解计数法的基本思路是指将M进制分解,即M=M1×M2×…×Mn,其中,M1,M2,…,Mn均不大于计数器最大计数N,此时用n片计数器分别组成M1,M2,…,Mn进制的计数器,然后级联构成M 进制计数器。本文主要采用分解法对72 位计数器进行设计分析。
2 分解法设计72 进制计数器
2.1 电路设计
采用分解法用74LS160N 设计七十二进制计数器时,有两种方法,分别计数9(九进制)个8(八进制)或8(八进制)个9(九进制)。在此采用高位八进制,低位九进制对电路进行设计。
电路设计时,低位计数器的状态在0001~1001,即在状态1~9 之间循环,需要利用状态1001 使计数器74LS160N 返回状态0001,在此引入一个2 引脚与非门,将1001 中为1 的高电平信号送至低位计数器的~LOAD引脚,读取预置数DCBA(0001),同时,利用低位计数器RCO 所产生的进位作为高位计数器的触发信号,接入高位计数器的CLK 引脚;同理,高位计数器的状态在0000~0111,即在状态0~7 之间循环,需利用状态0111 使高位计数器74LS160N 返回状态0000,在此引入一个3 引脚与非门,将0111 中为1 的高电平信号经与非门后送至高位计数器的引脚~LOAD 读取预置数DCBA(0000)。
需要注意的是计数器74LS160N 输入引脚D、C、B 和A 中,D 是高位,A 是低位;输出引脚QD、QC、QB 和QA中,QD 是高位,QA 是低位。
由于二进制状态不易观测,可以将二进制数变成十进制数来查看结果,此时需要接入数码管。
(2)与大豆产量挂钩的补贴政策效果不会改善政策的经济效率。根据国家发改委文件,大豆目标价格取消后会实施和玉米一样的生产者补贴政策,即实施与种植面积或产量挂钩的补贴政策。挂钩的补贴政策同样会产生扭曲,而且进口依存度越大产生的扭曲越大,政策的经济效率越低。实质上目标价格政策就是一种差价补贴,在市场环境没有发生改变的情况下,若取消目标价格政策转而实施与大豆产量挂钩的补贴政策仍不会提高政策的经济效率。
分解法设计72 进制电路如图1 所示。
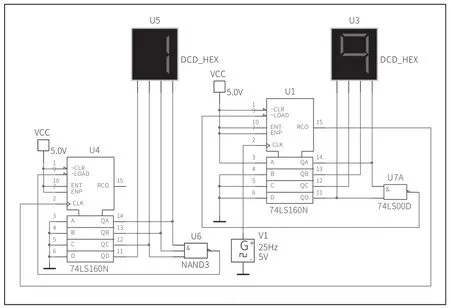
图1 72 进制计数器
在图1 中,U1 为低位计数器,其所对应的数码管U3数值变化在状态1 到状态9 之间循环,一次循环共计9 个状态,是九进制计数器;U4 为高位计数器,其所对应的数码管U5 数值变化从状态0 到状态7 之间循环,一次循环共计8 个状态,是八进制计数器。
电路运行后,U5=0,U3=1,当U3 每计1 到9 共9 个状态后,U5 会加1,一直运行到U5=7,U3=9 时,共计了8 个9,即72 种状态,是一个七十二进制计数器。此时如果电路继续运行,又会从U5=0,U3=1 这个状态开始。
在Multisim14.0 中对图1 所示电路进行仿真,电路运行后,却发现当U3 状态从1 变化到9 后,理论上U5 应该继续保持0,等到U3 变化为1 时,U5 变化到1。但电路运行后,数码管U5U3 变化为08、19、11,中间的状态09变成了状态19。如果电路继续运行,还会出现18、29、21,28、39、31……,至到68、79、71 等类似错误。
如果触发脉冲频率较高,这种错误会显得隐蔽。为便于分析错误产生原因,在此引入逻辑分析仪对高位和低位计数器的多路输出信号和触发信号进行观测。由于波形较多,为查看多引脚输出波形之间的关系,需要在电路中显示网络节点。
显示网络节点具体过程为:点击Multisim14.0 菜单Options, 选取Sheet Properties, 在选项卡Sheet visibility 中,对Net names 进行操作,选取show all,确认后即可显示电路中的各网络节点名称。网络节点名称是软件默认赋予,和电路连线顺序有关,电路中的“地”默认网络节点名为0。网络节点名可以修改,但不能重名。
用逻辑分析仪观测计数器U1、U4 的输出引脚QD、QC、QB 和QA 的输出波形,电路如图2 所示。
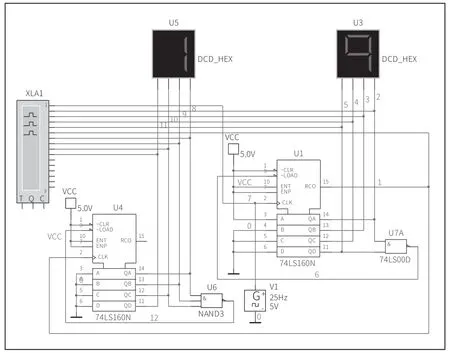
图2 72 进制计数器分析电路
在图2 中,低位计数器U1 的输出引脚QD、QC、QB和QA 所对应的网络节点名分别为5、4、3 和2,高位计数器U4 的输出引脚QD、QC、QB 和QA 所对应的网络节点名分别为11、10、9 和8,低位计数器触发信号所对应的网络节点名为7,高位计数器触发信号所对应的网络节点名为1。
运行图2 所示电路后,逻辑分析仪XLA1 的显示波形如图3 所示。
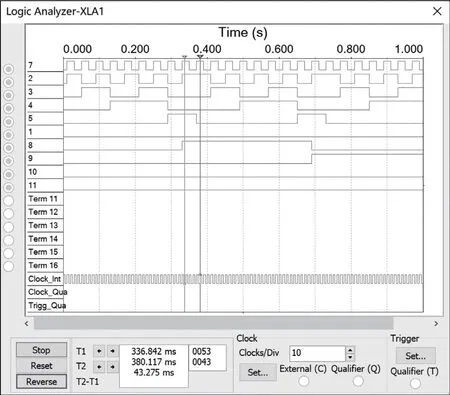
图3 逻辑分析仪输出波形图
注意,在图3 中,节点1 所对应的波形显示为0,不会发生变化,但实际上是有变化的,在节点8 由0 变化到1之前是有一个脉冲信号,该信号在示波器中可以观测到。
2.2 解决方法
为使理论与仿真实验一致,避免U5 的超前变化,可以在U1 的引脚~RCO 与U4 的引脚~CLK 之间添加与非门(非门)或延迟器对U4 的触发信号进行延迟。
2.2.1 添加与非门对高位触发信号延迟
根据与非门的传输延迟特性,在U1 的引脚~RCO 和U4 的引脚~CLK 中添加两个与非门对高位脉冲信号进行延迟,电路如图4 所示。
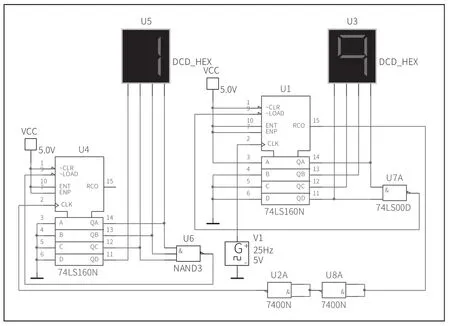
图4 与非门延迟高位触发信号电路
在图4 中选取2 个与非门7400N 进行级联,是因为要保持高位计数器U4 高电平触发。仿真逻辑分析仪XLA1 的结果与图3 波形一致,U5U3 显示时仍会出现09、19、11之类的错误。说明用与非门(非门)不好控制延迟时间,无法解决电路中存在的错误。
在实际仿真时,可用多个与非门级联,但仍不能保证低位触发信号传输速度快于高位信号传输速度,可见与非门进行信号延迟的方法不可行。
2.2.2 添加延迟器对高位触发信号延迟
在Multisim14.0 中,可以通过延迟器Delay 来模拟各种延迟情况,并对延迟时间自行设定,改变输入信号的传输速度,从而改变输出信号的时间。
在电路仿真时,可以在U1 的引脚~RCO 和U4 的引脚~CLK 之间添加一个延迟器,来延迟高位计数器的触发信号触发,使其慢于低位计数器的触发信号触发。
在计算延迟器延迟时间时,由于高位计数器的触发信号慢于低位计数器的触发信号,在设计时需要延迟。虽然延迟时间无法衡量,但延迟一个脉冲周期一定能保证高位计数器的触发信号慢于低位计数器的触发信号。
根据公式:
在已知低位计数器的时钟脉冲V1 的频率参数f=25Hz时,可以计算出T=0.04s。
即设置延迟器的延迟时间为0.04s,可以保证高位计数器的触发信号触发慢于低位计数器的触发信号。
添加延迟器对高位计数器触发信号进行延迟后,电路如图5 所示。在图5 中,A1 为延迟器,延迟时间设置为0.04s。
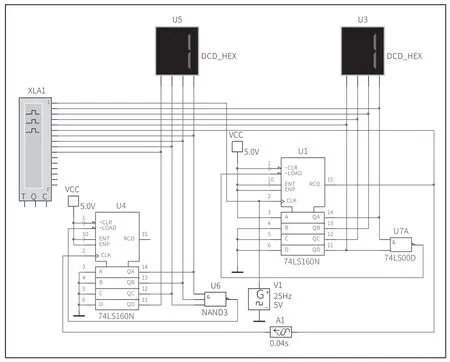
图5 延迟器延迟高位触发信号电路
运行图5 所示电路后,双击打开逻辑分析仪XLA1,运行结果如图6 所示。
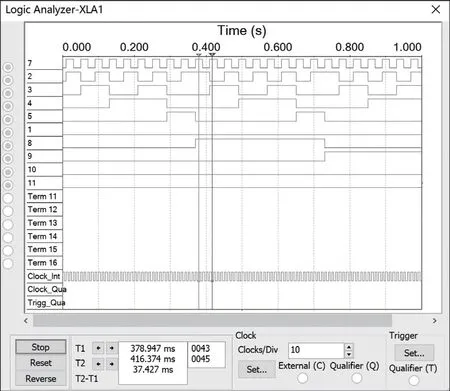
图6 逻辑分析仪输出波形图
由图6 的游标1 处可知U1 的输出(QD、QC、QB、QA) 是0001(XLA1 中显示的5、4、3、2 顺序) 时,U2 的输出QD、QC、QB、QA)是0001(XLA1 中显示为11、10、9、8 顺序),没有出现19 这种状态。此时理论与实际仿真相符。
这说明图6 所示电路可正确实现72 进制计数,低位U3 状态变化在1~9 这9 个状态之间循环,高位U5 状态在0~7 这8 个状态之间循环,计了72 个脉冲个数,实现了72进制计数。
3 结语
本文针对在用分解法设计计数器电路时,因为高位计数器接收到的触发信号传输速度快于低位计数器接收到的触发信号,导致高位计数器状态发生变化快于低位计数器状态变化,导致计数错误这一问题,在用逻辑分析仪对电路进行了深入分析,并引入与非门和延迟器对高位触发信号传输时进行延迟,使低位计数器的状态变化快于高位计数器状态的变化。但从电路仿真结果来看,与非门不能控制延迟时长,无法保证高位信号的延迟时间;而延迟器可根据低位计数器的触发脉冲频率设置延迟时间,可有效保证低位触发信号传输速度快于高位信号传输速度,从而解决用分解法设计计数器时高位计数器接收到的触发信号传输速度快于低位计数器接收到的触发信号这一问题。
