光谱共焦传感器多参数高准确度校准

杨品澒, 唐 波, 崔建军, 陈 恺, 宋佩颉, 彭 璐

(1.中国计量大学 计量测试工程学院，浙江 杭州 310018；2.中国计量科学研究院，北京 100029；3.甘肃省计量研究院，甘肃 兰州 730071；4.西藏自治区计量测试所，西藏 拉萨 850010；5.交通运输部 公路科学研究院，北京 100029)

1 引 言

光谱共焦传感器是一种基于光谱共焦成像原理[1]的非接触式单点紧凑型光学传感器,可实现高准确度的位移和厚度等的测量[2]。相对于激光干涉仪、电容式测微仪和光栅式测微仪等微位移测量仪器,光谱共焦传感器具有结构简单、抗干扰能力强、实时性高、层析特性好等优点,在微电子、医学仪器、工程材料以及航空航天等领域具有广泛的应用[3,4]。目前高准确度光谱共焦传感器的准确度已经达到了纳米级。例如,我国海伯森公司的光谱共焦传感器重复性为60 nm,深视智能公司的光谱共焦传感器重复性为12 nm,线性误差为300 nm;英国ZSY GROUP Ltd的EVCD10光谱共焦传感器在110 μm的量程内线性度为44 nm;德国MICRO-EPSILON的光谱共焦传感器在100 μm的量程内线性度为33 nm。这些日益提高的技术指标对其校准装置和校准方法在准确度上提出了更高的要求。而目前仍以测长机和激光干涉位移测量装置等通用计量设备为主,尚缺少专用的光谱共焦传感器校准装置。测长机准确度上仍然难以满足高准确度光谱共焦传感器的校准需求[5,6];而激光干涉位移测量装置虽然能够对准确度较高的光谱共焦传感器进行校准,但是由于存在周期性非线性误差[7～11],其峰峰值通常可达到6～20 nm,使得其测量准确度也难以进一步提高。对于高准确度位移校准装置而言,它的位移发生部件(如精密位移台)也往往存在几纳米甚至数十纳米的回程误差和重复性。这对于纳米级位移测量,会导致各受检点的位移标准值不完全一致,进而影响测量的准确性。

本文在传统激光干涉位移测量装置的基础上通过设计和优化测控方式等技术手段,构建了一种可满足光谱共焦传感器准确度要求的校准方法,通过提出的基于波长倍数的等间隔测量方法以及测点修正算法,减小了校准装置中激光干涉仪非线性误差和精密位移台定位准确度等对测量结果的影响,并设计了测量实验,给出了测量不确定度评定方法。

2 装置设计

2.1 光谱共焦传感器测量原理

白光源S发出的白光经过物镜L后照射在被测物体表面,多种单色光组成的白光经过物镜L,由于色散而形成不同波长的单色光,如图1所示。不同波长(λ1、λM和λ2)的单色光聚焦距离不同,各单色光中只有波长为λM的单色光能够在被测物体表面上M点处完全聚焦并被接收,而其它离焦状态的单色光不会被接收。

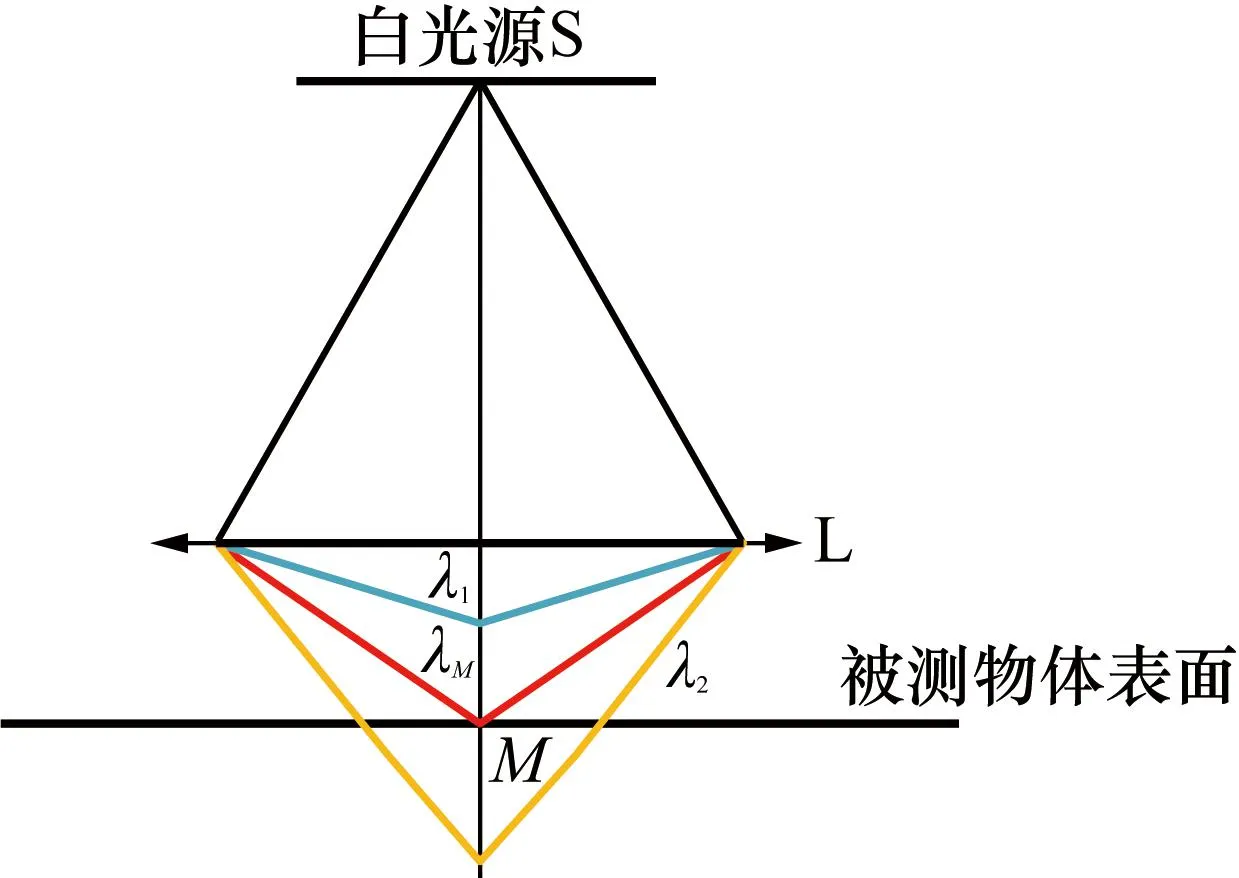
图1 光谱共焦原理图Fig.1 Color confocal principle drawing

被接收的波长为λM的聚焦光会形成峰值,通过对接收到的峰值波长进行解调计算,即可获得目标物体与物镜之间的相对距离[12]。轴向光学坐标位置与波长关系如式(1)所示:

(1)

式中:u为归一化的轴向光学坐标位置;λM为光学共焦系统的工作波长;δz为某一单色光聚焦点相对共焦焦点的实际轴坐标;a为色散物镜的孔径;f为色散物镜的焦距;kM为波数。

由光谱共焦测量原理可知,通过探测轴向光学坐标位置,可实现物体表面形貌以及位移距离等精确测量,在实际测量过程,测量结果还与被测物体表面的材质、光学反射率、粗糙度等物理属性相关[13～16],但是通过校准装置实现高准确度校准是它实现精密测量的技术前提和关键技术。

2.2 校准装置硬件设计

光谱共焦传感器校准装置(如图2所示)主要由激光干涉仪(激光器、光学组镜、环境补偿器等)、精密位移台、精密位移台控制器、反射板、测头夹具、计算机等组成。

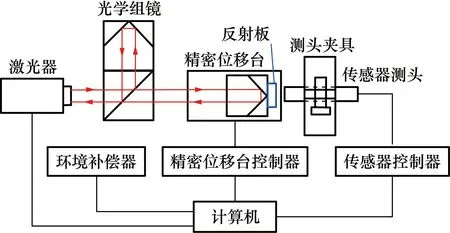
图2 光谱共焦传感器校准装置示意图Fig.2 Schematic diagram of calibration device for spectral confocal sensor

图2中,激光干涉仪的线性分辨率为0.1 nm,经检定知其测长不确定度(B类):U=5 nm+2.0×10-7L(k=2),用于提供位移标准值;精密位移台经校准知其技术指标:量程50 mm、最小步进2 nm、重复定位准确度30 nm、最大角晃动量5″,用于提供位移变化量;精密位移台控制器在计算机的指令下控制精密位移台的运动;反射板(白色陶瓷量块)固定在精密位移台上,并随精密位移台运动,且反射面垂直于运动轴线。测头夹具固定不动,用于夹持传感器测头,且保证其测量方向与精密位移台运动方向一致。环境补偿器用于对激光波长进行环境参数补偿;计算机获取激光干涉仪示值的同时,经传感器控制器实现光谱共焦传感器示值的同步采集。

2.3 校准装置软件设计

软件包括:仪器连接、位移控制、自动采集、环境补偿及数据分析模块。功能设计内容如图3所示。仪器连接模块用于实现计算机和激光干涉仪、精密位移台及被测光谱共焦传感器的数据通讯;位移控制模块内置控制算法(位移反馈控制),用于控制精密位移台的移动,同时用于设置测控过程的技术参数;自动采集模块用于采集激光干涉仪和被测光谱共焦传感器控制器的输出信号;环境补偿模块用于测量温度、气压和湿度等环境参数,计算空气折射率并对空气中的激光波长进行实时补偿;数据分析模块用于分析处理测量过程数据和解算被测光谱共焦传感器的计量特性参数。

图3 控制分析软件设计内容Fig.3 control analysis software design content drawing

软件各模块相互协作,使受检点之间的位移间隔为激光波长的整数倍,来减小激光干涉仪非线性误差对测量的影响;同时通过激光干涉仪示值反馈,实现了精密位移台定位准确度的提高。

3 关键技术

3.1 位移反馈控制

位移反馈控制的核心在于根据激光干涉仪示值调整精密位移台的位置,以显著提高校准装置的定位准确度。首先在测量前设定精密位移台的控制阈值;然后控制精密位移台按位移间隔ΔLi移动;最后计算激光干涉仪示值与ΔLi的差值,并用该差值与控制阈值进行比较。若该差值小于设定的阈值,则精密位移台按位移间隔ΔLi+1向下一个采集点进行移动。若差值大于控制阈值,则精密位移台将该差值作为位移量进行移动,移动完成后重新计算差值,并与控制阈值进行比较。反复进行上述过程,直到完成对N个受检点的采集。位移反馈控制的流程框图如图4所示。通过位移反馈控制,能够使精密位移台的位移量与设定值之间的差值不超过6 nm。

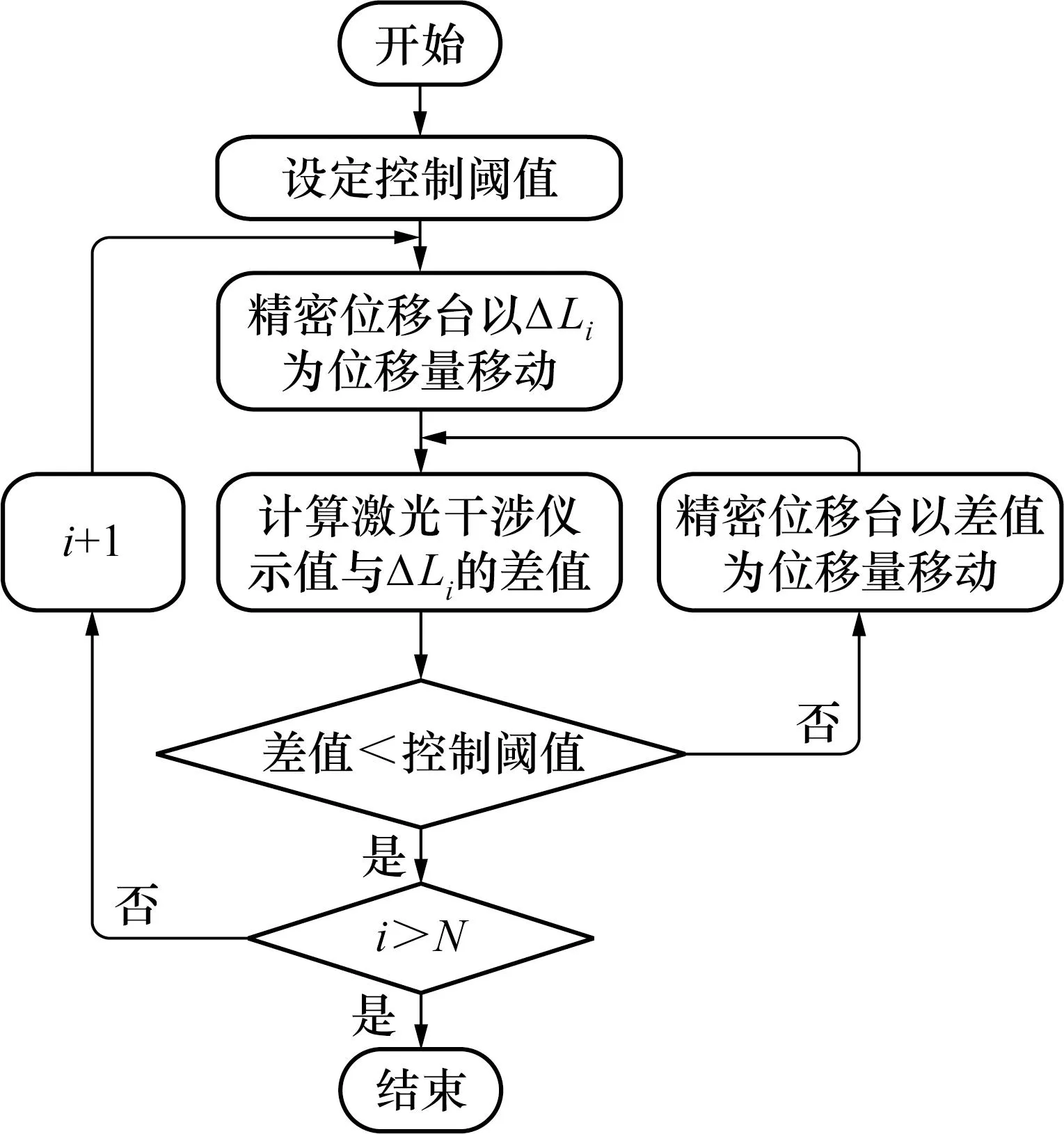
图4 位移反馈控制流程框图Fig.4 Displacement feedback control flow diagram

3.2 波长倍数间隔测量法

校准装置采用的激光干涉仪(波长λ约为633 nm),经中国计量科学院(NIM)的双频激光干涉仪标准装置测试,其存在周期为λ/2的非线性误差,其幅值的峰峰值10 nm,测试结果如图5所示。

图5 激光干涉仪非线性误差Fig.5 Nonlinear error of laser interferometer

可通过对位移间隔进行取整,使其长度为激光波长的倍数,来减小激光干涉仪非线性误差对测量结果产生的影响。通过取整运算,如式(2)所示。

(2)

式中:ΔLi为第i个受检点的位移间隔;[]表示取整;N为采集点数;λ为激光干涉仪的波长;YFS为光谱共焦传感器的标称满量程。

该方法可以使激光干涉仪非线性误差对位移测量的影响降低至2 nm甚至更小,从而提高了激光干涉仪使用时的测量准确度。

3.3 测点修正算法

由于精密位移台的定位准确度远大于激光干涉仪示值,使得在同一受检点各次测量的激光干涉仪示值不完全相同,导致被测光谱共焦传感器的重复性、回程误差和线性度等技术指标无法直接计算。故而提出了测点修正算法,其原理是:在某受检点处,被测光谱共焦传感器示值减去激光干涉仪示值,得到的差值作为某受检点处的示值误差。下面分析该算法的可行性。

设i为受检点序号,j为测量行程次序数,受检点位置为xi,Sij为激光干涉仪示值,Yij为被测光谱共焦传感器示值,Δij为二者的示值误差。则有:

Δij=Yij-Sij

(3)

激光干涉仪示值Sij与受检点位置xi的间距dij为:

dij=Sij-xi

(4)

随着受检点位置变化,被测光谱共焦传感器示值与激光干涉仪示值存在线性关系,如图6所示。

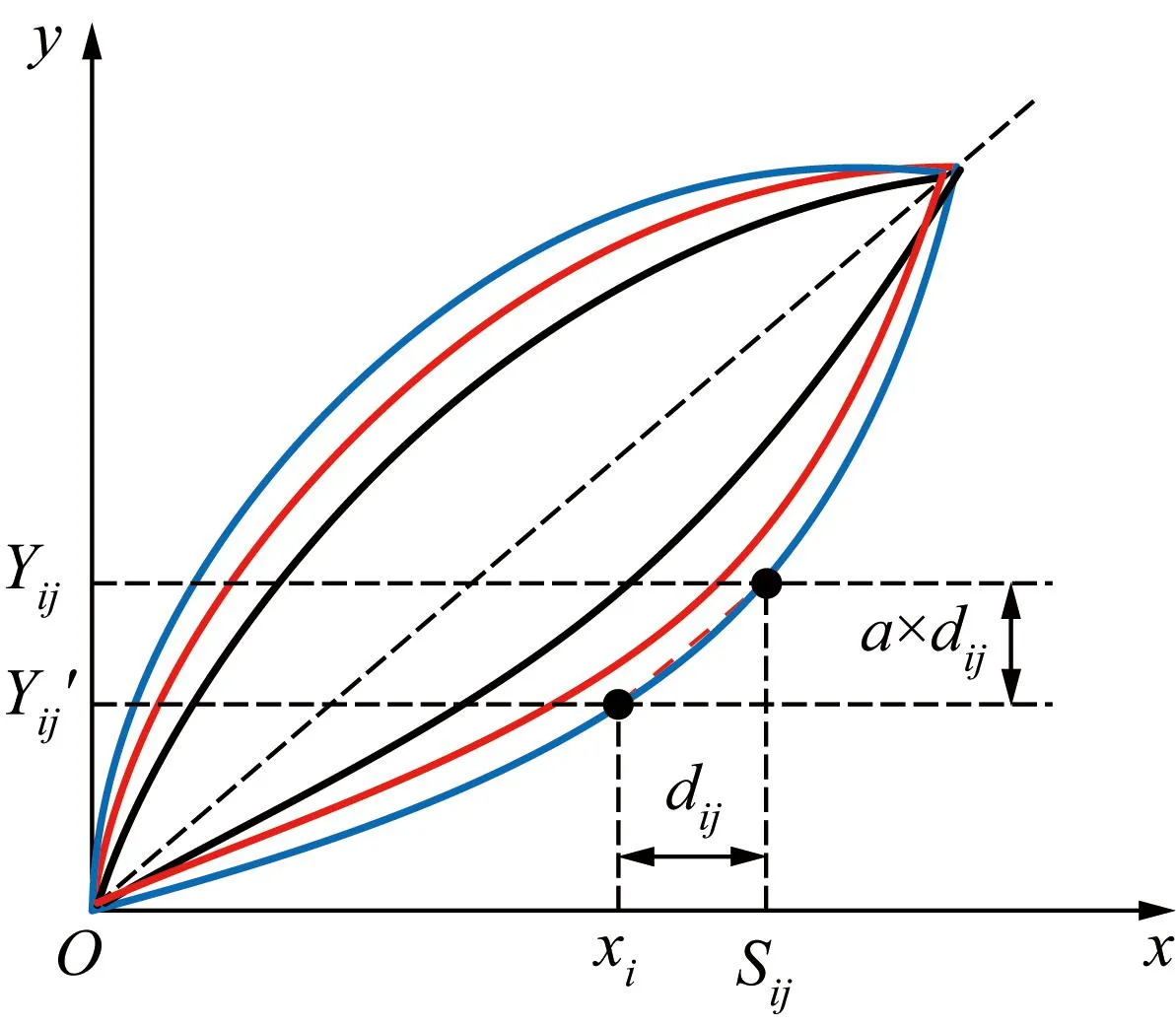
图6 示值变化线性关系图Fig.6 Linear relationship of indicated values drawing

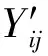
(5)

(6)

(7)

若激光干涉仪示值Sij与受检点位置xi相距较远,即dij较大时,式(7)会引入较大误差,此时的示值误差为:

(8)

不同斜率a与不同间距dij时,测点修正算法引入的偏差如表1所示。

表1 不同斜率和间距时测点修正会引入的偏差Tab.1 The bias introduced when the measurement point is corrected with different slope and spacing

4 测量实验

4.1 实验过程

对某量程为100 μm的光谱共焦传感器的示值误差和重复性进行测量。

在实验过程中,将被测光谱共焦传感器的测头固定在测头夹具上,通过光学准直技术,调整传感器测头的位置和姿态,以确保测量过程符合阿贝原则。精密位移台进行移动,计算机同步采集激光干涉仪和被测光谱共焦传感器控制器的示值,并进行分析处理。

4.2 实验结果

1) 参照JJF 1663—2017《激光测微仪校准规范》[17],各受检点的示值误差计算如式(9)所示:

(9)

式中:δi为第i个受检点的示值误差。各受检点示值误差结果如图7所示。

图7 示值误差校准曲线Fig.7 Indication error calibration curve drawing

由测量数据分析可得,在100 μm量程内,示值误差为±0.02%,用绝对数值表示,则最大的示值误差约为±23 nm。

2) 参照JJF 1305—2011《线位移传感器校准规范》[18],第i个受检点的重复性如式(10)所示:

(10)

式中:ri为第i个受检点的重复性;Δi为各点同向行程中的最大差值,μm。各受检点的重复性如图8所示。

图8 重复性校准曲线Fig.8 Repeatability calibration curve

被测光谱共焦传感器在100 μm量程内,重复性为0.005%,用绝对数值表示,则重复性为5 nm。

5 测量不确定度评定

5.1 不确定度来源

不确定度来源包括:被测光谱共焦传感器的分辨力或重复性引入的不确定度分量u1(Yij),激光干涉仪波长稳定性引起的不确定度分量u2,λ(Sij),激光干涉仪非线性引入的不确定度分量u2,e(Sij),空气折射率引起的不确定度分量u2,n(Sij),激光干涉仪光轴与精密位移台运动轴线不平行引起的不确定度分量u3,p(Sij),被测光谱共焦传感器的测量轴线与精密位移台运动轴线不平行引起的标准不确定度分量u3,s(Sij),精密位移台角晃动引起的不确定度分量u3,a(Sij)及环境温度变化引入的不确定度分量u4(Sij)。

5.2 不确定度传播公式

合成不确定度如式(12)所示:

(12)

不确定分量的传递系数如式(13)、式(14)所示:

(13)

(14)

式中:urel(Yij)为与被测光谱共焦传感器有关的不确定度分量;urel(Sij)为与校准装置有关的不确定度分量;YFS=100 μm;c(Yij)=0.01 μm-1;c(Sij)=-0.01 μm-1。

5.3 标准不确定度评定

1) 被测光谱共焦传感器的分辨力或重复性引入的不确定度分量u1(Yij)

被测光谱共焦传感器的测量分辨力为0.1 nm,可视为均匀分布,引入的不确定度分量u1(Yij1)=0.03 nm。

重复性为5.0 nm,引入的不确定度分量u1(Yij2)=2.9 nm。

该不确定度分量包含了分辨力引入的不确定度分量u1(Yij),因此选择重复性引入的不确定度c(Yij)u1(Yij)=0.0029%。

2) 激光干涉仪波长稳定性引起的标准不确定度分量u2,λ(Sij)

激光波长相对扩展不确定度(B类):Uτ(λ)=2.0×10-8(k=2),波长稳定性引入的不确定度分量u2,λ(Sij)=1.0×10-8L,c(Sij)u2,λ(Sij)=0.000 001%。

3) 激光干涉仪非线性引入的标准不确定度分量u2,e(Sij)

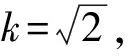
4) 空气折射率引起的标准不确定度分量u2,n(Sij)

空气折射率引入的相对扩展不确定度(B类),U2,n(Sij)=2.0×10-7(k=2),引入的不确定度分量u2,n(Sij)=1.0×10-7L,c(Sij)u2,n(Sij)=0.00001%。

5) 激光干涉仪光轴与精密位移台运动轴线不平行引起的不确定度分量u3,p(Sij)

6) 被测光谱共焦传感器的测量轴线与位移台运动轴线不平行引起的标准不确定度分量u3,s(Sij)

同理,当被测光谱共焦传感器打在反射板上的光点最大偏移量为0.07 mm时,不确定度分量u3,s(Sij)=0.2 nm,c(Sij)u3,s(Sij)=0.000 6%。

7) 精密位移台角晃动引起的不确定度分量u3,a(Sij)

8) 环境温度变化引入的不确定度分量u4(Sij)

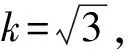
U2=k×uc=7.0 nm。

表2 标准不确定度分量分析表Tab.2 Standard uncertainty component analysis table

计算结果为u0=1.5 nm+1×10-7L,取包含因子k=2,校准装置的扩展不确定度

U1=3.0 nm+2×10-7L,

测量结果的合成标准不确定度

取包含因子k=2,扩展不确定度

6 讨 论

在校准过程中发现,换用不同材质、粗糙度的测量板,得到的校准结果会存在差异。当选择光学反射镜作为反射板时,被测光谱共焦传感器无有效信号输出;当采用白色零级陶瓷量块作为反射板时,其校准结果目前来看最佳,而采用零级钢量块时次之,金属面作为反射板时最大示值误差最大。不同反射板的测量结果如表3所示。

表3 不同反射板对测量的影响Tab.3 The influence of reflection plates of different materials on measurement

7 结束语

采用激光干涉仪实现纳米级位移测量是目前较为普遍应用的技术方法,但由于激光干涉仪非线性误差的影响,限制了测量准确度的提高。本文提出的波长倍数间隔测量法,可在不改变激光干涉仪技术性能的条件下,配合精密位移台,通过改变测量的过程和方式,来减小激光干涉仪非线性对位移测量的影响,进而提高位移测量的准确度,这为很多纳米级甚至更高准确度的位移测量提供了技术思路。针对纳米位移测量往往受限于精密位移台等位移发生部件的精度限制,也提出了测点修正算法来简化实际应用中的数据处理过程,并在理论上分析了算法对偏差的影响规律,这对简化分析过程和提高分析效率具有积极意义。采用本文提出的技术方法和研制的校准装置,不仅可解决高准确度的光谱共焦传感器的校准问题,也可为更大量程的纳米位移传感器的校准、研发和生产提供技术支持。