优化动态核主元分析的工业过程故障监测方法

杨 芳， 王亚君， 沈亚慧

（辽宁工业大学电子与信息工程学院，辽宁锦州 121001）

0 引 言

故障监测一直是研究热点。复杂工业过程往往具有非线性、动态、多模态、高维度、间歇性等特点，使得故障监测变得非常复杂。传统的故障监测方法已经无法满足故障监测的要求，需要采用更加先进的技术实现更准确地故障监测［1-3］。Scholkopf等［4］提出了核主元分析（KPCA）方法，该方法使用核函数实现某种非线性映射，解决了之前存在的线性映射无法解决的问题。Chen等［5］提出了BDPCA（batch dynamic PCA）和BDPLS（batch dynamic PLS）算法，然而扩展数据阵的有效范围受时滞长度的限制，仅能反映局部时间段内的动态特性。Wang等［6］提出了一种基于多动态核主元分析（MDKPCA）的复合降维故障监测方法。将自回归移动平均时间序列模型和KPCA 方法相结合，建立动态核主元分析（DKPCA）模型，对工业过程中的非线性和动态进行处理。

目前KPCA方法作为一种非线性主元分析方法被广泛运用，KPCA 方法的有效性依赖核函数参数的选取，因此关于核函数参数的研究一直是近几年的热点。Chapelle等［7］提出了利用梯度下降法解决核函数优化问题，但需要计算目标函数对优化参数的偏导数。如果目标函数对某个参数的偏导数不存在，或者由于计算复杂而难以求解，梯度下降法就不能有效地进行核函数优化。Zhang等［8］进行了核函数参数优化方法的比较研究，其中包括二分法、基于反向传播（BP）神经网络的重构法以及基于样本分类的重构法，并设计了一个核函数参数优化系统进行核函数参数优化，但存在计算量较大的问题。Chen 等［9］提出了一种改进的遗传算法，用于核函数优化。将核函数的类型和参数作为决策变量，并通过优化编码方案、遗传策略、适应度函数、交叉和变异算法等方法最小化均方根误差。为了确保核函数的多样性，采用二折交叉验证法对训练结果进行验证，但该方法容易陷入局部最优。

针对上述问题，提出了一种基于人工大猩猩部队优化动态核主元分析（GTO-DKPCA）的故障监测方法。首先将数据进行预处理，然后利用时间序列模型和KPCA方法建立故障监测模型，最大化人工大猩猩部队优化算法对正常数据和故障数据之间的几何距离来寻找最优参数。为了验证该方法的有效性，给出了青霉素发酵故障监测工艺案例。

1 动态核主元分析

1.1 核主元分析过程

KPCA方法主要解决非线性问题，基本思想是：使用非线性映射将原输入空间映射到一个髙维的特征空间F中，然后在该特征空间中进行主成分分析计算，从而把原始空间的非线性问题转化为高维空间的线性问题。KPCA方法在提取数据非线性主要成分的同时保留了原始数据结构，很好地解决了非线性特征变换问题，也不会损失数据的重要特征。KPCA方法如下：

设样本数据xk∈Rm（k＝1，…，N），其中N为样本点个数。令F为特征空间，将样本数据映射到特征空间：xk→F，映射后的数据为Φ（xk）。协方差矩阵计算式为

对应特征方程为

式中：λ为非零特征值；v为特征向量。式（2）等价于

存在系数αi（i ＝1，2，…，N），使得特征向量v＝结合式（2）、（3）得

为了避免特征空间计算复杂，引入核函数K，化简可以得到Nλα ＝Kα，其中K满足中心化公式INK－KIN＋INKIN，IN＝1／N。计算过程详见文献［10］。第m个KPCA的特征主元通过映射得到，计算过程为

式中：um为非线性主元；q为非零特征值个数；vm为对应的特征向量；αi，m为um对应的系数；m＝1，2，…，q。

1.2 动态核主元分析过程

为了解决生产过程中的动态特性，构造动态自回归移动平均时间序列模型［11］。当前时刻每个采样点的变化主要与时间序列的历史数据有关，利用时间序列历史相关特性在每个采样点处增加前d个历史时刻上的采样点。时间序列模型与KPCA方法相结合称为DKPCA方法。DKPCA方法可以很好地去除动态系统中输入与输出的关系，能够更好地监测故障。扩展后的数据矩阵为：

式中：Xd为扩展数据矩阵；H为每个批次建模数据矩阵的采样点；d为时滞长度。

1.3 相关统计量与控制量计算

DKPCA方法的统计量和控制量与PCA方法的统计量类似，但对于DKPCA方法，需要在特征空间中进行计算。在特征空间中平方预测误差（SPE）统计量计算方法为

假设预报误差服从χ2分布，此时特征空间中SPE统计量的控制限可由式（7）计算得到。在特征空间中，霍特林统计量T2计算方法也与PCA方法类似，具体计算方法为

式中，Λ－1为对角阵的逆矩阵。对角阵由与um相对应的主元方差构成，故特征空间中T2控制限可由式（8）计算获得。

2 基于人工大猩猩部队优化算法的核函数参数优化

2.1 核函数选取

将核函数的内积代替复杂的非线性映射来处理非线性问题。通过核函数可以将测量样本数据映射到高维特征空间，在高维特征空间中应用线性主元分析，因此核函数的选取尤为重要。由文献［12］可知，多项式核函数、径向基核函数（RBF）和Sigmoid 核函数是常用的核函数。研究表明［13-15］，径向基核函数对数据的处理更好，因此选择径向基核函数。径向基核函数表达式为

式中：c为核函数参数，表示径向基核函数的宽度。在进行非线性特征变换时，核函数参数的选取对DKPCA方法的监测性能有着重要的影响。合适的核函数可以对数据进行更精准的特征提取，有效地避免了非线性情况下数据不可分的难题，从而提高故障监测的准确性和可靠性。传统的核函数参数一般由人为主观测试或交叉验证等方法选取。人为选取用时较长，而交叉验证方法需要大量的计算。因此，提出了GTO-DKPCA方法，利用优化算法对核函数参数进行优化，得到最优参数。

2.2 人工大猩猩部队优化算法

元启发式算法在解决优化问题时起着至关重要的作用，GTO算法灵感来自大猩猩在自然界中的社会行为［16］。在GTO 算法的初始化过程中先设置相应参数，然后在探索空间中随机初始化种群。Q为种群数量，M为最大迭代次数。β 为大猩猩暴力程度公式中的参数，其值为0.3。w是开发阶段2 种机制的控制参数，其值为0.8。探索阶段模型为：

式中：G（t＋1）为大猩猩下一次迭代时的位置；Y（t）为当前大猩猩的位置；r1、r2、r3和rand 为每次迭代更新范围0 到1 的随机值；p为介于0 到1 之间的给定参数；U、L为变量的上、下限；Yr（t）和Gr（t）为随机选取大猩猩的位置；t为当前迭代次数。在每次更新位置分别计算D、B、R，计算式为：

式中：r4为迭代时更新从0 到1 的随机值；l为0 到1之间的随机数；Z为区间［－D，D］内的随机数。在探索阶段结束时，计算G（t）和Y（t）的适应度，如果G（t）适应度小于Y（t），则Y（t）被G（t）代替。因此，该阶段产生的最优个体也被视为银背大猩猩。在GTO 算法的开发阶段，模拟了大猩猩的2 种行为：跟随银背大猩猩和成年雌性竞争。这2 种行为通过D进行切换，当D≥w时，选择跟随银背大猩猩，相反则进行竞争。跟随银背大猩猩机制的表达式为：

式中：Ysilverback为最优解；Ga（t）为迭代时每只候选大猩猩的位置。成年雌性竞争机制的表达式为：

式中：I为大猩猩竞争强度；r5为0 和1 之间的随机数；A为用来模拟竞争程度的系数；O为暴力对解决方案维度的影响。rand为0 到1 之间的随机数。当rand≥0.5 时，O等于正态分布和问题维度中的随机数；反之，O等于正态分布中的随机数。人工大猩猩部队优化算法模拟如图1 所示。

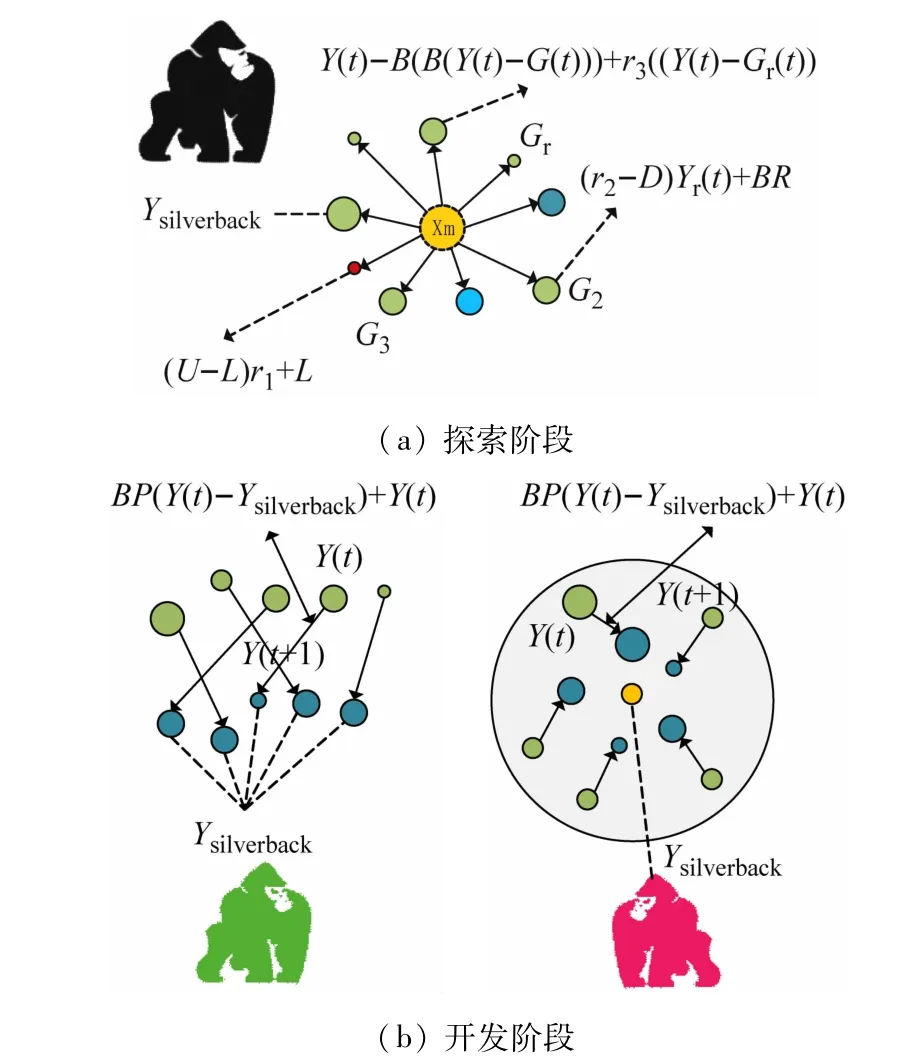
图1 人工大猩猩部队优化算法模拟

2.3 基于GTO-DKPCA故障监测方法

采用GTO方法优化径向基函数的参数c，使用自适应度函数进行故障监测。给定数据集，计算正常数据集与故障数据集之间的类间几何距离与数据点到最近类距离的比值，目标是最小化距离比值的平均值。该自适应度函数能够适用于正常数据集和故障数据集，从而提高故障监测的准确性。该适应度函数定义为

式中：Sd为数据间的散度矩阵；Sb为数据中的散度矩阵。根据正常数据与故障数据之间的关系，建立适应度函数，利用适应度函数对核函数参数寻优，更好地平衡正常数据和故障数据之间的差异，提高故障监测的准确性和可靠性。

3 实验验证

青霉素发酵生产过程是一个典型的非线性、动态性和间歇性过程。在仿真实验中对通风率、搅拌功率和底物供给速率3 种常见故障类型进行研究。青霉素发酵过程中，前2 种故障主要影响温度和溶解氧浓度，从而影响青霉素的产量和质量。正常工况下采集30批次建模数据作为训练数据。各批次的反应时间设定为400 h，进行数据采集时采样间隔为0.05 h，建模和在线监测时采样间隔为1.00 h。初始条件和设定值范围如表1 所示。

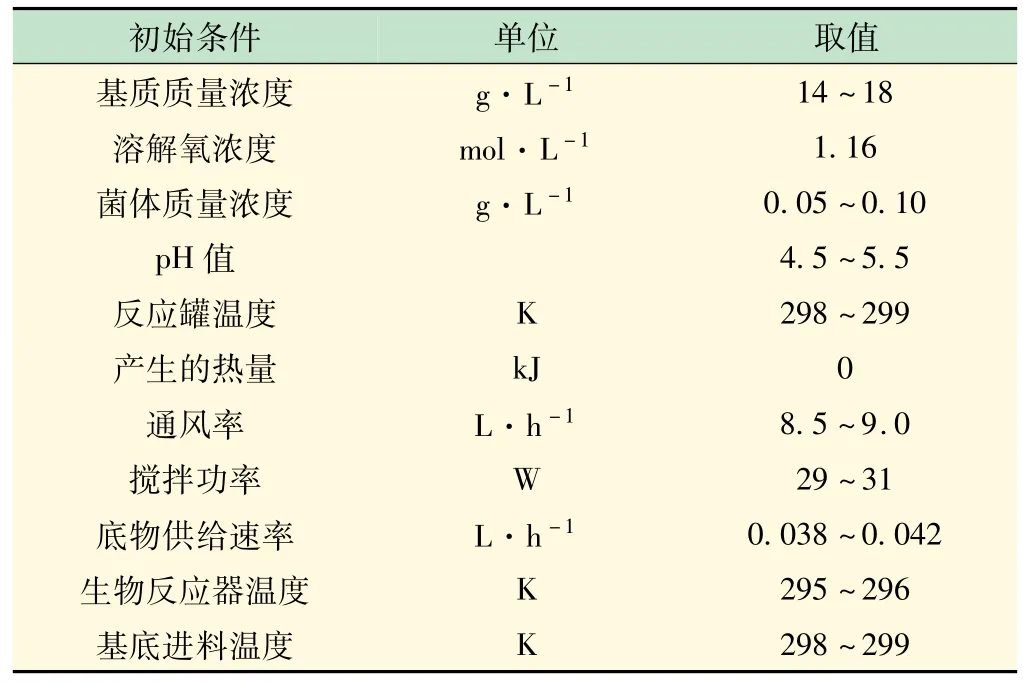
表1 发酵过程初始参数取值

在青霉素发酵过程中，30 批次的训练数据中包含10 个变量8 000 个数据，在利用GTO算法对径向基核函数参数进行优化时，对正常数据与故障数据的类间几何距离最大适应度函数寻优，最终得到优化后参数。采用GTO算法进行优化的适应度曲线如图2 所示。

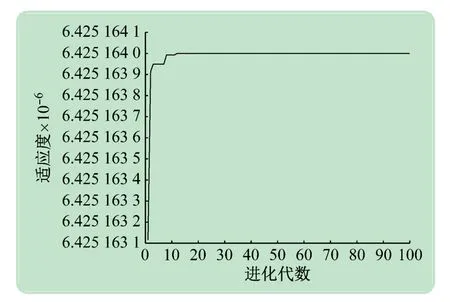
图2 适应度曲线

为了验证所提方法的有效性，在正常工况下采集30 批次建模数据，分别建立多向核主元分析（MKPCA）、BDKPCA、GTO-DKPCA 模型。采用置信水平为99%的控制线进行在线监测。表2 列出了青霉素发酵过程的3 种测试情况：搅拌功率阶跃跳变、通风率线性变化、底物供给速率线性变化。

表2 青霉素发酵过程中的3 种模拟场景

图3 为故障1 监测结果。在故障1 中，通风率在200 h时以0.05 的斜率线性降低，直至反应结束。对于MKPCA方法（见图3（a）），T2统计量在211 h时发生偏差，SPE统计量在207 h时发生显著偏差，T2统计量故障监测延迟了11 h，SPE 统计量故障监测延迟了7 h。BDKPCA方法的监测结果如图3（b）所示，SPE统计量从205 h开始监测到故障，而T2统计量从209 h开始监测到故障。GTO-DKPCA 方法能够在203 h 时监测到故障。MKPCA和BDKPCA方法不能够很明显地监测出异常情况，而GTO-DKPCA 方法能够很好地监测出异常，如图3（c）所示。当干扰在200 h 引入时，相较于MKPCA 和BDKPCA 方法，GTO-DKPCA 方法监测能力更强。

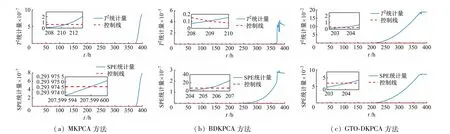
图3 故障1监测结果

由于底物供给速率的快慢会对青霉素产量产生影响，因此将底物供给速率在50 h 时增加10%至结束。如图4（a）所示，MKPCA方法进行故障监测时，SPE 和T2统计量均在50 h之前就监测出故障，将正常数据作为故障数据；如图4（b）所示，BDKPCA 方法进行故障监测时，T2统计量在62 h 监测出故障，SPE 统计量在39 h监测出故障；如图4（c）所示，GTO-DKPCA方法监测故障时，T2统计量在59 h 时监测出故障，SPE 统计量在51 h时监测出故障。相较于MKPCA与BDKPCA方法而言，GTO-DKPCA方法能够更好地监测故障。

图4 故障2监测结果

对于故障3，搅拌功率从100 h 开始阶跃增加10%直至反应结束。搅拌功率变化将直接影响总体氧气质量系数K1a，而K1a的降低导致培养基中溶氧水平降低，进而降低了生物量增长和青霉素浓度。图5（a）、（b）分别为MKPCA 和BDKPCA 方法的监测结果。MKPCA 无法有效地监测出故障，而对于BDKPCA，在101 h时SPE统计量监测出故障，但T2统计量仍不能监测出故障。GTO-DKPCA 方法能够成功地监测出故障，如图5（c）所示。

图5 故障3监测结果

4 结 语

提出了一种GTO-DKPCA 故障监测方法。首先，根据正常数据和故障数据的特点，利用GTO方法对核函数参数进行优化，使DKPCA模型的监测效果更好。通过计算特征空间中的T2和SPE统计量，有效地提取过程变量之间的非线性关系，从而实现更佳的监测性能。在青霉素发酵过程中应用GTO-DKPCA方法进行故障监测。监测结果表明，GTO-DKPCA 方法比MKPCA和BDKPCA方法更准确地监测出故障，具有更为优越的监测性能。