植被最大光能利用率的模拟方法对比评估

赵涔良，朱文泉，谢志英

1.北京师范大学 遥感科学国家重点实验室,北京 100875;

2.北京师范大学 地理科学学部 北京市陆表遥感数据产品工程技术研究中心,北京 100875

1 引言

植被总初级生产力（GPP）的定量估算有助于理解陆地生态系统碳循环及植被与气候的相互作用（方精云等，2001；袁文平等，2014；Anav等，2015）。目前已有多种估算GPP 的方法（Monteith，1972；Farquhar等，1980；Liu等，2002；朱文泉等，2007；Badgley等，2019），其中，光能利用率模型因其充分利用了遥感数据的连续观测能力及大空间覆盖范围的优势而得到了广泛应用（Monteith，1972；Potter等，1993；Xiao等，2005；Yuan等，2014）。光能利用率模型是一种具有一定生理生态过程基础和较强实用性的参数模型（Running等，2000；Yuan等，2007），光能利用率（LUE）是其核心参数。LUE 是指植物吸收单位辐射光的CO2吸收量，是一个可观测的实际生理参数（Hammer 和Wright，1994；Medlyn，1998），它通常由最大光能利用率（LUEmax）参数结合温度、水分等环境胁迫因子计算得到。

LUEmax参数对植被生产力的估算精度有着重要影响。早期的CASA 模型在计算植被净初级生产力（NPP）时将所有植被类型的LUEmax参数设置为0.389 g/MJ（以碳计）（Potter等，1993），模拟的NPP 误差较大；MODIS-LUE 之后的植被生产力估算模型则开始根据不同的植被类型采用不同的LUEmax参数值，GPP/NPP 的模拟精度有所提升（Running等，1999；Xiao等，2004；朱文泉等，2006；Yuan等，2007）；而近期的一些研究则认为LUEmax参数应随季节而变化，通过采用随季节变化的LUEmax参数，GPP/NPP 的模拟精度相较于原静态LUEmax参数有明显提升（Muramatsu等，2014；Lin等，2017；Zhou和Xin，2019）。

目前，调整LUEmax参数的方法可分为3 大类：基于植被指数的方法、基于叶面积指数（LAI）的方法和基于统计的方法。各种植被指数及其对应的参数调整算法构成了基于植被指数的LUEmax参数调整方法（Thanyapraneedkul等，2012），其中Muramatsu等通过拟合GPP和光合有效辐射（PAR）的矩形双曲线，通过对比7种植被指数发现基于叶绿素指数（CI）模拟的LUEmax参数值表现最优，并进一步对7 种植被类型（分布于日本区域的7 个通量站点）月尺度的LUEmax参数进行了模拟，发现LUEmax参数具有明显的季节性变化特征，且模拟的LUEmax参数值在7种植被类型中都低于MODIS-LUE模型的原静态LUEmax参数值（Thanyapraneedkul等，2012；Muramatsu等，2014）。多种不同的包含LAI的季节调节因子算法构成了基于叶面积指数的LUEmax参数调整方法（Kosugi等，2003；Limousin等，2010），其中多数方法仅适用于涵盖了完整生长季的LAI 时序数据，而Zhou 等（2019）基于北美区域的6个落叶阔叶林通量站点数据，通过在原模型结构上附加LAI季节调节因子使得LUEmax参数能够进行近乎实时的调整计算；其在年尺度的实验结果显示，对于北美的落叶阔叶林植被类型，调整的LUEmax参数在MODIS-LUE、VPM（Xiao等，2004）、RP（Xin等，2016）和VI（Wu等，2010）模型中，GPP 的模拟精度都优于未进行参数调整的原模型。基于统计的方法中，Lin 等（2017）使用了概率统计方法而非频数统计方法——马尔可夫链蒙特卡洛方法（MCMC），模拟了北半球中高纬度8 种植被类型的月尺度LUEmax参数（46 个站点），发现月尺度的LUEmax参数在单叶模型（MODIS-LUE）和双叶模型中均能够显著提高植被生产力模型的拟合度（R2）并降低均方根误差（RMSE），且在所有植被类型上的GPP 模拟精度都优于MODIS-LUE模型的原静态LUEmax参数。

尽管近20年来在通量观测数据的支持下已发展了许多新的光能利用率模型，但是这类模型在GPP 估算方面仍存在较大的不确定性（Chen等，2014；Dong等，2015）。使用通量观测数据修正或添加模型参数的方式仍然不能较好地反映植被GPP 的季节性变化（Hashimoto等，2013）。在模型中允许LUEmax参数随季节而变化，能够使模型更加贴合叶片对环境条件变化作出适应性反应的实际情况（Houborg等，2009）。因此，从调整LUEmax参数的角度改进模型，能够使其估算的GPP在季节变化特征上与实际观测的GPP 尽量地贴近（Muramatsu等，2014；Lin等，2017；Zhou 和Xin，2019）。然而，已有的调整LUEmax参数的相关研究大多局限于特定的植被类型或空间范围，且缺乏各动态LUEmax参数间的横向对比。因而这些动态LUEmax参数在更广泛的植被类型和区域的适用性，以及不同的动态LUEmax参数模拟方法在地域间的适用性差异等问题仍不明确，而澄清这些问题将有助于降低区域和全球范围内GPP估算的不确定性。

因此，本文从3 大类动态LUEmax参数模拟方法中各自选出最具代表性的方法——基于叶绿素遥感指数（Muramatsu等，2014）、基于LAI季节调节因子（Zhou 和Xin，2019）、马尔可夫链蒙特卡洛模拟（Lin等，2017），通过采用相同的生产力估算和评估数据集（FLUXNET 2015 数据集）及模型结构（MODIS-LUE 生产力模型结构），在相对更广的研究区域内（更多的通量站点与植被类型）对它们进行对比分析，评估模拟的动态LUEmax参数与原静态LUEmax参数在MODIS-LUE 模型框架下的GPP估算精度，以期揭示不同的动态LUEmax参数在各植被类型上的季节性变化特征及差异以及各LUEmax参数在GPP估算方面的精度差异。

2 数据与方法

2.1 数据

本文从FLUXNET 2015（https：//fluxnet.org/［2021-06-10］）下载了其下所有的通量观测数据，并依据下述原则对数据进行了筛选：（1）站点的观测年限＞2年；（2）站点对应的遥感数据质量较好（低质量标签记录占比＜10%），最终筛选出了包含12种植被类型的200个站点，共计887条站点年记录。其中，位于北半球的站点有172个，位于南半球的站点有28 个（站点植被类型缩写对应IGBP 分类系统，12 种植被类型分别为耕地、草地、湿地、郁闭灌丛、稀疏灌丛、稀树草原、多树草原、落叶阔叶林、常绿阔叶林、混交林、落叶针叶林、常绿针叶林）。FLUXNET 2015 数据集中的平均气温、最低气温、饱和水汽压差（VPD）以及短波入射辐射数据被用于计算MODIS-LUE 模型中的各项模型参数（光合有效辐射、温度胁迫系数、水分胁迫系数等），而通量观测的总初级生产力（GPP）数据则作为评估各模拟方法的依据。FLUXNET 2015 中天尺度的原始数据被整理至8 天尺度用以匹配遥感数据计算GPP。

MCD15A2H 数据集中的fPAR 数据（500 m，8 d）被用于计算8 天尺度的GPP。MOD09A1 数据集中的近红外（NIR）和绿光（Green）反射率数据（500 m，8 d）被用于计算叶绿素指数（CI）。上述数据均通过质量标签进行了筛选，每一个通量站点的对应数值是其中心坐标周围9宫格内有效像元的均值。

2.2 MODIS-LUE模型及不同的LUEmax参数设置

本文所选的3 种动态LUEmax参数模拟方法（基于叶绿素遥感指数、基于LAI 季节调节因子和马尔可夫链蒙特卡洛模拟）都是仅针对LUEmax参数进行考虑，而并非针对植被生产力模型整体结构进行改进，且其在各自的原文献中均使用了MODIS-LUE 模型结构对比评估了动态LUEmax参数的优势。因此，为了能够在相同的模型结构下对比各LUEmax参数，本文选用了MODIS-LUE 模型（Running等，1999），并结合各种LUEmax参数来计算GPP。MODIS-LUE的模型结构如下：

式中，PAR 是单位时间（例如每天或每月）的入射光合有效辐射，MJ/m2），fPAR 是表示被植被吸收的光合有效辐射（APAR）占总入射光合有效辐射的比例；Ts-Tmin是使用最低温度作为输入参数的温度胁迫因子；Ws-VPD是使用饱和水汽压差作为输入参数的水分胁迫因子；LUEmax是最大光能利用率（g/（m2·MJ），以碳计），各模拟方法有着不同的参数设置（表1），依据各自对应文献中所描述的算法进行计算。

表1 各动态LUEmax的参数设置Table 1 Parameter settings for each dynamic LUEmax

2.3 评估方法

将基于各LUEmax参数计算的GPP与通量站点观测的GPP 进行对比，GPP 的模拟效果采用拟合度（R2）和均方根误差（RMSE）进行评估（Willmott等，1985；Willmott和Matsuura，2005）。

将基于动态LUEmax参数模拟的GPP精度与基于静态LUEmax参数模拟的GPP 精度进行对比，动态LUEmax参数的改进效果采用拟合度变化值（ΔR2）和均方根误差变化值（ΔRMSE）进行评估。

组间的差异显著性检验采用单因素方差分析，P＜0.05表示差异显著。

3 结果与分析

3.1 各LUEmax参数在不同植被类型下的特征

3 种动态LUEmax参数在不同植被类型上都与MODIS-LUE 模型原静态LUEmax-BPLUT参数有着明显差异，并且具备明显的季节变化特征（图1，制图时进行了以2 为底的对数变换处理，y 轴不等间距）。可见：基于叶绿素遥感指数的LUEmax-CI参数，在落叶阔叶林、草地、常绿针叶林、混交林植被类型上的季节变化特征明显，呈现出单峰特征；而在耕地、常绿阔叶林类型上的季节变化特征则相对不明显，呈现水平波动的特征。此外，LUEmax-CI参数的数值在落叶阔叶林、落叶针叶林、混交林植被类型中全年低于MODIS-LUE 模型原静态LUEmax-BPLUT参数，而在常绿阔叶林、草地植被类型中则全年高于原静态LUEmax-BPLUT参数。基于叶面积指数的LUEmax-LAI参数在各植被类型中的季节变化特征都较为明显，在郁闭灌丛、稀树草原植被类型中呈现单峰特征；在落叶阔叶林、常绿阔叶林、常绿针叶林、多树草原植被类型中则呈现双峰特征；在耕地、落叶针叶林、混交林、稀疏灌丛、湿地植被类型中则呈现“U”型特征。另外，LUEmax-LAI参数与MODIS-LUE模型原静态LUEmax-BPLUT参数的数值差异极大，生长季的LUEmax-LAI参数数值与LUEmax-BPLUT参数数值最为接近，但是在非生长季则会明显高于LUEmax-BPLUT参数数值。基于马尔可夫链蒙特卡洛模拟方法的LUEmax-MCMC参数仅在部分植被类型上有着较为明显的季节变化特征，其在落叶阔叶林、稀疏灌丛植被类型上呈现单峰特征，在常绿针叶林、多树草原植被类型上呈现“U”型特征，而在其余的耕地、郁闭灌丛、常绿阔叶林、草地、混交林、稀树草原、湿地植被类型上则呈现水平波动特征。同时，LUEmax-MCMC参数数值在部分植被类型中与MODIS-LUE 模型原静态LUEmax-BPLUT参数数值较为接近，其在静态LUEmax-BPLUT参数附近上下波动（落叶阔叶林、稀树草原、湿地、多树草原）。不过，在其余植被类型上，LUEmax-MCMC参数数值都整体低于或高于MODIS-LUE模型原静态LUEmax-BPLUT参数数值。

图1 3种动态LUEmax参数在不同植被类型中的月变化Fig.1 Monthly variation patterns of three dynamic LUEmax parameters on different vegetation types

综上，各动态LUEmax参数与MODIS-LUE 模型原静态LUEmax-BPLUT参数在数值上有着明显差异，且不同动态LUEmax参数间也有明显的横向差异。然而，不同动态LUEmax参数间仍具有一定的一致性（例如落叶阔叶林的生长季，3 种动态LUEmax参数的年变化曲线都呈现凸型），但是在具体植被类型上的表现有着较大的差异。

3.2 各LUEmax参数下的GPP模拟精度

从模型拟合度（R2）来看，基于不同LUEmax参数计算的GPP 结果间有着明显差异（图2）。可见：不区分植被类型时，3 种动态LUEmax参数中基于LUEmax-LAI和LUEmax-MCMC的GPP估算结果相比基于原静态LUEmax-BPLUT参数的GPP 估算结果在拟合度上占优（图2（b）和（d）），而基于LUEmax-CI的GPP估算结果在总体拟合度上则不及基于LUEmax-MCMC和LUEmax-LAI参数的结果，且比基于原静态LUEmax-BPLUT参数的GPP估算结果要差（图2（a）和（c））。区分植被类型时（图3（a）），基于LUEmax-CI和LUEmax-MCMC的GPP 估算结果仅在DNF的春季相比基于原静态LUEmax-BPLUT参数的GPP 估算结果在拟合度上有明显下降（LUEmax-MCMC，除落叶针叶林以外的植被类型ΔR2=-0.02 — 0.09；LUEmax-CI，除落叶针叶林以外的植被类型ΔR2=-0.03 —0.04。图3（a）中 的LUEmax-CI参数和LUEmax-MCMC参数在落叶针叶林植被类型的春季ΔR2分别为-0.59和-0.46，且p＞0.05）；基于LUEmax-LAI参数的GPP 估算结果则差异较大（ΔR2=-0.19 — 0.27），在部分植被类型上其估算GPP 的拟合度明显低于基于原静态LUEmax参数估算GPP的拟合度（例如常绿针叶林、混交林植被类型），而在另一部分类型中则相反（例如郁闭灌丛植被类型夏秋季）。区分时段来看（图3（b）），3 种动态LUEmax参数中基于LUEmax-LAI和LUEmax-MCMC的GPP 估算结果在全年多数时段均优于基于原静态LUEmax-BPLUT参数的GPP 估算结果（LUEmax-MCMC的ΔR2为0.03 — 0.14，LUEmax-LAI的ΔR2为-0.02 — 0.15）。而基于LUEmax-CI参数的GPP 估算结果在全年都不及基于原静态LUEmax-BPLUT参数的结果（LUEmax-CI的ΔR2为-0.27 — -0.02）。

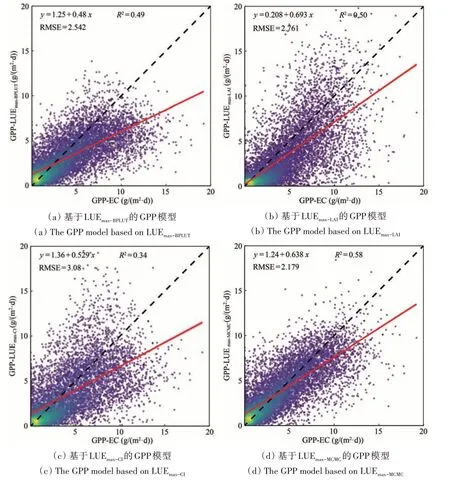
图2 基于不同LUEmax参数的模型GPP估算精度对比（GPP单位均以碳计）Fig.2 Comparisons of GPP estimation accuracy among models with different LUEmax parameters（The GPP units are showed in carbon）

图3 基于动态LUEmax参数与基于静态LUEmax参数的GPP估算效果（R2）对比Fig.3 R2 comparison of estimated GPP between dynamic and fixed LUEmax parameters

从对GPP 模拟的误差（RMSE）来看（图4），基于动态LUEmax参数计算的GPP 结果与基于静态LUEmax参数的计算结果在不同的植被类型、不同时段内均有着不一样的表现。区分植被类型来看（图4（a）），LUEmax-MCMC以碳计的ΔRMSE 为-158.0 —3.2 g/（m2·季），表现最优；LUEmax-LAI以碳计的ΔRMSE为-146.7 — 79.2 g/（m2·季），表现次之；LUEmax-CI以碳计的ΔRMSE 为-106.8 — 224.5 g/（m2·季），表现最差。区分时段来看（图4（b）），3 种动态LUEmax参数计算的GPP，仅有基于LUEmax-MCMC参数的GPP 估算结果在全年所有月份都优于基于原静态LUEmax-BPLUT参数的GPP 估算结果（LUEmax-MCMC的ΔRMSE为-17.0 — -2.3 g/（m2·月），以碳计）；基于LUEmax-LAI参数的GPP估算结果在6 — 8月劣于原静态LUEmax-BPLUT参数的GPP估算结果（LUEmax-LAI的ΔRMSE为-0.9 — 12.9 g/（m2·月），以碳计）；LUEmax-CI参数的结果则是全年各月均不及原静态LUEmax-BPLUT参数（LUEmax-CI的ΔRMSE 为 9.9 — 20.2 g/（m2·月），以碳计）。

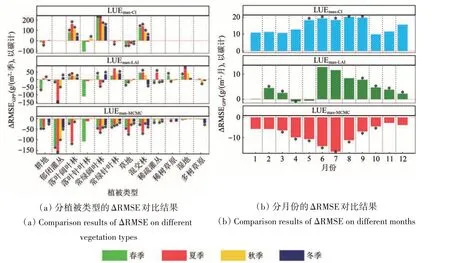
图4 基于动态LUEmax参数与基于静态LUEmax参数的GPP估算效果（RMSE）对比Fig.4 RMSE comparison of estimated GPP between dynamic and fixed LUEmax parameters

从组间差异显著性检验的结果来看，4 种LUEmax参数的GPP估算数值存在显著差异。总的来说，LUEmax-MCMC的GPP估算结果最优（相比静态参数的GPP结果，以碳计的ΔRMSE=-10.9 g/（m2·月），ΔR2=0.084），其次是LUEmax-LAI（以碳计的ΔRMSE=6.5 g/（m2·月），ΔR2=0.042），LUEmax-CI表现最差（以碳计的ΔRMSE=16.1 g/（m2·月），ΔR2=-0.15）。

4 讨论

4.1 LUEmax参数的季节性变化特征

在更广范围内对LUEmax参数的横向对比结果显示，不同动态LUEmax参数在各植被类型上的季节性变化特征有显著差异，且也与其原研究中的实验结果存在不同。例如，基于叶绿素遥感指数方法的LUEmax-CI参数在原研究区内的常绿针叶林、落叶阔叶林类型中的季节性变化特征与本研究存在一定差异：对于常绿针叶林类型，原研究在日本区域的结果呈现水平波动的季节变化特征，且数值全程低于原静态LUEmax-BPLUT参数（Muramatsu等，2014），而本文显示LUEmax-CI参数在常绿针叶林类型上有着明显的季节变化，呈现出单峰曲线特征，曲线在生长季有小幅度的凸起，并且生长季阶段的数值高于原静态LUEmax-BPLUT参数（图1）；落叶阔叶林类型上的结果也类似，其原研究的结果呈现水平波动特征，而本研究的结果则是呈现波动水平较小的单峰曲线。此外，本研究基于LUEmax-MCMC参数在部分植被类型上的结果与其原研究也存在差异。对于草地类型，原研究的LUEmax-MCMC参数呈现明显的U形特征（Lin等，2017），而本文则呈水平波动。

造成上述差异的原因，一方面可能是原研究区的季节变化特征受限于其单一的局地气候，另一方面也可能是同一植被类型下群落物种的差异所致。已有研究指出LUEmax参数的季节性变化与LAI 及冠层结构有着紧密的关系（Teh等，2000），并且其数值的变化可以通过环境温度进行解释（Medlyn等，2002；Xu 和Baldocchi，2003；Zhu等，2011）。本文在分析LUEmax参数的影响因子方面与同类研究有着类似的结论，详见图5。典范对应分析CCA（Canonical Correspondence Analysis）本质是多响应变量多元回归结果的主成分降维展示，其排序结果图中各箭头之间的角度表示相关性的大小，两箭头方向垂直则为不相关，锐角表示正相关，钝角为负相关，而散点的坐标位置则是各样本点在CCA1 和CCA2 上的投影。分析结果同时也给出了影响因子的方差，各影响因子中解释度最高的是温度胁迫系数（Ts）和LAI，其次则是饱和水汽压差（VPD）和水分胁迫系数（Ws），这一方面佐证了LUEmax参数与LAI 指数和温度的紧密联系，另一方面也暗示除温度外的其他环境因素也可能会对LUEmax参数产生影响，未来对LUEmax参数的模拟需要进一步考虑各种影响植物生理的环境参数。此外，图5 中除去LUEmax-MCMC参数和原静态LUEmax-BPLUT参数有较好的正相关性，但是总体上3 种动态LUEmax参数之间的相关性一般（图5，LUEmax-CI参数仅适用于7 种植被类型，因而12 种植被类型仅有7 种植被类型被纳入CCA 分析）。这说明不同数据基础所刻画的季节性变化特征存在明显差异，从而导致了各LUEmax参数在时序变化特征、植被类型适用性以及GPP 估算精度方面有着不同的表现。

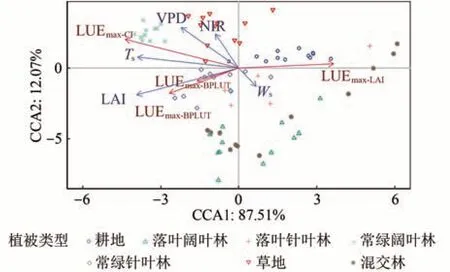
图5 LUEmax参数与环境影响因素间的相关性分析Fig.5 Correlation analysis between LUEmax parameters and environmental influencing factors

4.2 各LUEmax参数对GPP估算精度的影响

基于3 种动态LUEmax参数的光能利用率模型相比原静态LUEmax参数模型，在GPP 的估算方面有一定程度的改善，但是不同动态LUEmax参数之间差异较大，且没有同静态LUEmax参数拉开明显的差距。例如，基于LUEmax-LAI参数的光能利用率模型，虽然在郁闭灌丛、落叶针叶林以及常绿阔叶林植被类型上相比静态LUEmax参数模型有着明显的提升，但是该方法在植被覆盖较稀疏的非林地、非郁闭灌丛类型上的结果则不如静态LUEmax参数模型（图3（a）、图4（a））。总的来说，LUEmax-MCMC参数在全植被类型的所有时段，其GPP 的估算精度都不低于原静态LUEmax-BPLUT参数（以碳计的ΔRMSE=10.9 g/（m2·月），ΔR2=0.084），并且在郁闭灌丛、落叶针叶林以及常绿阔叶林植被类型上的提升效果尤为明显。同类研究对基于LUEmax-MCMC参数的GPP 计算结果在植被类型上的适用性差异给出了解释，其认为站点数量和观测样本较多的植被类型在Metropolis-Hasting 方法中会占据更多的权重，因而模拟出的LUEmax参数在不同植被类型估算精度的改善上存在差异（Lin等，2017）。但是本文在通量站点数据更为充足的条件下，使用MCMC方法对每个植被类型的LUEmax参数进行了独立的模拟，但仍旧存在类似的适应性差异，因此本文倾向于认为原静态LUEmax-BPLUT参数对一些植被类型（郁闭灌丛、落叶针叶林、常绿阔叶林）在GPP 估算上有着较其余植被类型稍大的原始系统误差，并且也已有相关研究指出静态单叶模型在常绿阔叶林植被类型上的GPP 估算精度的确不及其他植被类型（Yuan等，2014；Anav等，2015）。此外，上述结果也说明了基于不同数据基础的LUEmax模拟方法对不同的植被类型和时间段存在适用性差异，并且基于植被指数的方法会更适用于林地等植被覆盖较密的地区。

基于动态LUEmax参数的光能利用率模型对GPP 估算精度的改善程度存在季节性差异。同基于静态LUEmax参数的模型相比，基于LUEmax-LAI参数在6 — 8月之外的时段有着显著优于原静态LUEmax-BPLUT参数的结果（图3（b）、图4（b）中的符号*标记），而LUEmax-MCMC参数则是在全年各月都优于原静态LUEmax-BPLUT参数。同类研究认为这是由于各类静态LUEmax参数模型（Potter等，1993；Veroustraete等，1994；Xiao等，2004；Turner等，2006；Yuan等，2007；Mahadevan等，2008）的LUEmax参数多来自于生长季旺季的观测或是基于良好生长状态的假设（Lin等，2017；Zhou 和Xin，2019）。

4.3 评估结果的应用展望及局限性

Houborg 等（2009）认为动态LUEmax能够使模型更加贴合叶片对短期环境条件变化作出适应性反应这一实际情况，从而有利于更加准确地计算总初级生产力。然而，LUEmax参数与植被生理状态密切相关，除了温度、LAI、水分等因素外，营养元素限制、林龄、散射辐射比例等因素也会对其产生影响。但是这些因素中，除CFlux 光能利用率模型对林龄因素进行了考虑（Turner等，2006），其余因素在大部分单叶光能利用率模型中都未有对应的模型参数设计。因而在现有的模型结构中，添加影响LUEmax的相应因素的模型参数并同时对所有的模型参数进行统一率定，会有助于提高光能利用率模型的GPP估算精度。

本文研究结果主要基于FLUENET 2015通量站点，然而这些通量站点在植被类型上的数量并不均匀，且也不够充足，将来需在扩大通量观测以及结合无人机遥感、叶绿素荧光指数（SIF）、光化学反应指数（PRI）等新方法或工具的基础上进一步研究。

5 结论

本研究采用相同的生产力估算数据集（FLUXNET 2015 数据集）及模型结构（MODISLUE 生产力模型结构）在相对更广的研究区域内（更多的通量站点与植被类型）横向对比了3 种典型动态最大光能利用率参数（LUEmax）的季节性变化特征，并评估了他们在MODIS-LUE 模型框架下的GPP估算精度，得到如下两个主要结论：

（1）3 种动态LUEmax参数（基于叶绿素遥感指数、基于LAI季节调节因子、马尔可夫链蒙特卡洛模拟）之间相互差异较大，他们在各植被类型上的季节性变化特征不同，其年内变化曲线呈现单峰、“U”型及水平波动3种特征。

（2）基于动态LUEmax参数的GPP估算精度相比基于原静态LUEmax参数有着一定的提高，但高度依赖于具体的动态LUEmax参数，部分动态LUEmax参数仅在特定的植被类型与时段相比原静态LUEmax参数对GPP 估算有提升效果，而在某些植被类型与时段甚至会造成更大的估算误差（以碳计的ΔRMSE最高可达20 g/（m2·月），ΔR2最低可达-0.27）。总体而言，贝叶斯框架下的马尔科夫链蒙特卡洛（MCMC）方法对动态LUEmax参数有着较好的模拟效果（相比静态参数的GPP结果，以碳计的RMSE总体降低了10.9 g/（m2·月）），并且其GPP 的估算精度在全植被类型的所有时段都不低于原静态LUEmax参数，并且在郁闭灌丛、落叶针叶林以及常绿阔叶林上的提升效果尤为明显。