正六边形蜂窝型空腹楼盖挠度计算方法对比分析

2024-04-16刘宇杰杨晓华何嘉杰张泽良

上海建材 2024年1期

刘宇杰，杨晓华，何嘉杰，张泽良

（湖南工业大学土木工程学院，湖南株洲 412007）

0 引言

在当今社会经济建设及科学技术发展的飞快进程下，各领域对多层大跨度建筑的要求越来越高，对大跨度空间的要求也越来越高，这促使几代学者、专家对各种新型结构体系进行了深入探究[1]，以满足建筑平面造型上和空间的需要，同时达到经济技术指标和力学性能的要求。钢-混凝土组合楼盖是一种新型楼盖[2]，其来源得益于钢框架结构与混凝土梁板结构的不断发展，一般由型钢梁、混凝土板组成楼盖。将混凝土楼盖中的梁替换为型钢梁，再通过抗剪连接件将2 种构件组合，使其共同受力，发挥钢材抗拉强度高、混凝土板抗压性能好的特性[3]。

20 世纪末，贵州大学的马克俭院士提出了空腹夹层板盒式结构这一新型空间结构，在此基础之上研究出了钢空腹夹层板楼盖结构，这是一种新的空间网格结构。该结构以钢筋混凝土空腹夹层板楼盖理论为基础，通过用型钢做上下肋以及钢管（圆形或方形）做剪力键，照常使用混凝土板作为表层板。相较于传统的钢筋混凝土空腹夹层板，钢空腹夹层板具有多项优势[4]：1）施工时不需要模板，制作上下肋和剪力键时无需养护，故施工周期缩减良多；2）在约束楼盖高度的情况下，钢空腹夹层板的跨度要比传统钢筋混凝土空腹夹层板大很多；3）在大、中型公共建筑以及工业厂房中获得了良好的实用成效，与装配式结构的结合效果也很好。

近年来，空腹夹层板楼盖已成为一种备受关注的新型楼盖技术。学者们对这种能够同时减少建筑物重量并提升其刚度和强度的新型结构体系持有非常乐观的态度，众多学者对空腹夹层板楼盖的计算方法进行了广泛研究。

张华刚等[5]采用拟夹层板，假定了计算中面的存在，并建立了空腹夹层板楼盖的基本方程，引入了2个位移函数，用于表示3个广义位移，并将基本方程简化为关于位移函数的联立方程组，从而成功地解决了这一问题。为对实际工程提供设计参考，张华刚等[6]利用有限元软件观察了8节点弹性块体在竖向荷载作用下的结构反应，并分析了其变形形式和内力的分布情况，研究了空腹夹层板的承载力设计问题，还详细比较了空腹夹层板实用计算方法和有限单元法的承载力结果。肖建春等[7]基于结构等效原则，推导出折算剪切刚度的计算公式，该公式是基于空腹网架拟交叉梁系法推导的，考虑了面板的作用和上、下弦层构件不对称的影响，从而扩大了该方法的适用范围，另外还提出了一个适用于空腹夹层板的折算剪切刚度计算式，该公式除考虑了上述因素外，还考虑了剪力键的剪切变形影响，适用于I型和Ⅱ型板。试验分析表明，这些公式均具有较高的精度。赵子斌[8]提出了一种针对钢筋混凝土空腹夹层板楼盖结构的分析方法，称为等效挠度法，基于实用计算方法-等效刚度法，并对实际工程中的经济技术指标进行了分析。经过理论推导与验证，该方法表现出可靠的理论依据，验证的空腹梁模型与实腹梁模型的计算误差均在5%以内，满足了工程计算精度要求。

综上所述，当前空间结构研究的热点趋向于正六边形蜂窝型空腹夹层板楼盖，但因为该结构的设计计算比较繁杂，所以进一步确定其简化计算模型很有必要。因此，本文利用连续化方法、实用计算方法与有限单元法3 种空腹夹层板楼盖的计算方法来计算楼盖挠度，对比分析其差异，以期为相应的设计提供一些有价值的参考。

1 连续化方法分析

钢混组合的空腹夹层板楼盖结构也归类于空腹网格结构之一，其中使用的型钢梁与圆管薄壁钢剪力键都有着薄壁宽肢的特质，然而构造却跟钢筋混凝土空腹夹层板楼盖结构有所不同。但2 种楼盖结构因力学模型相似，可以采用连续化方法对其进行结构分析[9]。采用连续化方法分析时，空腹夹层板楼盖结构的抗剪刚度是有限的[10]，因此连续化方法即考虑结构剪切变形的拟夹层板法。

1.1 计算基本假设

对于配置非常繁密上下肋梁的空腹夹层板，平面网格的布设相对来说较为紧密，短跨方向板的网格数应大于4。拟夹层板的上表层是根据混凝土薄板及空腹夹层板的上肋等效而成的，故而假设拟夹层板上表层在混凝土薄板的形心处，不考虑肋与板的偏心影响。在计算中，将空腹夹层板的下肋等效为下表层夹层板，假定下表层位于下肋截面形心处，即不计上、下表层的厚度，不计横向剪力作用，仅考虑在平面内受的轴力。空腹夹层板里设置的剪力键被等效成拟夹层板的夹心层，夹心层的厚度即为剪力键的高度h，夹心层只受到横向剪力而不受轴力作用。

假设垂直于板面的直线段在变形以后仍为一条直线，在挠曲之后与板面不再互相垂直，而是在yz、xy平面内分别变化了一个角度ψx和ψy，即ψx≠∂ω/∂x,ψy≠∂ω/∂y，其中ω为挠度函数。

等效后的拟夹层板因上、下表层刚度的差别而没有了对称面；在计算时，上表面被选取为参考面,建立基本方程。基于以上假设，可根据弹性力学中横向剪切变形的非经典平板理论建立基本方程。

1.2 上、下表层刚度

在建立基本方程之前，因令拟夹层板等效替代钢网格空腹夹层板，故先求出空腹夹层板的等效平面刚度，经由连续化处理的平面交叉杆系如图1所示。

图1 肋系轴力与平面内力的关系Fig.1 Relationship between axial force and plane internal force of rib system

一般情况下的上下肋为多组交叉的肋系，针对表层的第i组杆系，其物理方程[11]如下：

式中：Ni为轴力；E为弹性模量；Ai为截面面积；εi为轴向位移。

由肋系轴力Ni可知平面内力为：

式中：li为第i向肋的间距；αi为x水平轴与xi轴的夹角。

根据弹性力学，肋系的应变εi与平面内的应变εx、εy和εxy的关系可以表示为：

将式（5）代入式（1）可得：

再将上式代入式（2）～式（4）可得

将其表示为矩阵形式：

式中：[B]L为肋等效平面刚度矩阵。

空腹网架的网格体系一般有3 种（见图2）：正交正放、正交斜放与三向网格。考虑到施工方便，其各向肋的几何尺寸均相同，对于三类网格体系，可分别写出其肋的等效平面刚度。

图2 空腹网架的网格体系Fig.2 Grid system of open web grid

由式（12）～（14）可知，三向网格是一种各向同性体，三向网格的平面刚度极其接近平板平面刚度，完全等效于厚度为δ、泊松比v= 1/3的各向同性板。

对于以上3 种网格形式，肋的等效平面刚度矩阵皆可表示为：

其中，各刚度系数分别为：

空腹夹层板楼盖结构中混凝土薄板刚度平面可表示为：

1.3 等效剪切刚度

以双向网格体系推导空腹夹层板一榀单方向空腹板架的折算剪切刚度计算公式。用拟交叉梁系法计算钢网格空腹夹层板的夹心层等效剪切刚度。在满足1.1 节的基本假定外，补充以下假定：1）剪力键截面相同；2）上下肋的反弯点在杆件中间；3）忽略扭转变形。以剪力键为中心，典型区间的网格尺寸为Δ。上肋材料弹性模量为E1，截面惯性矩为I1；下肋材料弹性模量为E2，截面惯性矩为I2；剪力键弹性模量为Ev，截面惯性矩为Iv，将此区间等效成尺寸为Δ×h、刚度相同的梁元，等效梁元原理如图3 所示。

图3 等效梁元原理示意图Fig.3 Schematic diagram of equivalent beam element principle

在此区间的剪切单元中，上、下弦构件剪力分别为V1、V2，水平力为H，剪切单元总剪力为V。由平衡原理可知：

用图乘法计算区间剪切单元的剪切变形γ0：

因为剪力键自身尺寸问题：宽度大、高度小，需计算自身剪切应变：

式中：k为剪应力不均匀系数[13]；Gv为剪力键的剪切模量；Av为剪力键截面面积。

因此，典型区间剪切单元最终剪切应γ为：

即等效钢元的剪切变形γ′为：

式中：C为折减剪切刚度。

得出第i组肋系剪力Qi为：

式中：γi为xi方向的横向剪切应变。

因此得出拟夹层板的剪力Qx与Qy，即：

由材料力学可知，任意方向的横向剪切应γi=γxcosαi+γysinαi，可得：

将其改写成矩阵形式：

其中，[C]的系数表达式分别为：

3种空腹夹层板网格形式的剪切刚度矩阵如下。

（1）正交正放网格。令i=1、2，a1=0，a2=π/2，则有：

剪切刚度矩阵为：

（2）正交斜放网格。令i=1、2，l1=l2=l，a1=π/4，a2=-π/4，C1=C2=C，则有：

剪切刚度矩阵为：

（3）三向网格。令i=1、2、3，l1=l2=l3=l，a1=0，a2=π/3，a3=-π/3，C1=C2=C3=C，则有：

剪切刚度矩阵为：

1.4 基本方程

由基本假定确立拟夹层板上表层作为计算参考面，用拟夹层板的转角ψx、ψy和挠度γ建立基本力学方程。

（1）拟夹层板的几何方程为：

式中：εa、εb为上、下表层的平面应变；χ为拟夹层板的弯曲应变，计算参考面如图4所示。

图4 计算参考面Fig.4 Calculation reference surface

（2）拟夹层板物理方程为：

式中：Na、Nb为上、下表层内力：N为整体的轴力；M为整体的弯矩；Q为横向剪力。

根据式（32）可解得εa与M：

式中：b为拟夹层板的薄膜柔度矩阵；K为拟夹层板的耦合矩阵；D为拟夹层板的抗弯刚度矩阵。

各矩阵表达式如下：

（3）平衡方程。空腹夹层板一般只承受施加在混凝土薄板的均布面荷载，拟夹层板的平衡方程为：

连续性方程为：

引入应力函数ϕ，可得：

用应力函数ϕ与转角ψx、ψy表示M、εa，可得表达式如下：

式（47）和式（48）是以应力函数ϕ与3 个广义位移ψx、ψy、ω为主未知量的基本微分方程。

2 实用计算方法分析

对空腹夹层板楼盖结构进行结构软件计算，常使用空腹夹层板楼盖结构实用计算方法，该方法以抗弯刚度等效为原则，将楼盖结构中的上下肋简化为上下表层薄板，剪力键简化为薄板之间的夹心层，如图5所示。

蜂窝型空腹夹层板楼盖高为h0，实腹H 型钢梁高为h1，可得：

设b=b1，f=f1，可得：

3 有限单元法分析

有限单元法是以结构矩阵分析为原理的数值分析方法，随着计算机技术的飞速发展，其在实际工程中的应用越来越广泛。目前有限单元法可提供各种充足的单元种类与形式，其采用结点位移与位移导数构造板、实体等单元，可基本符合实际工程的各种限制与要求。

有限单元法对于各种场景皆适用，无几何形状、边界条件、荷载布置的约束，材性亦不受制于各向同性。此外，有限单元法能结合具有行为相异和不同数学描述的分量，借助对网格的划分大小进行调整，从而对精度进行调控。有限单元法计算步骤是：先将结构离散化为若干单元，再用结点把这些单元体连接起来。赋予每个单元不同编号并求解刚度矩阵，再将不同单元的刚度矩阵综合为整体刚度矩阵。结构受力是平衡的，边界条件矩阵由整体刚度和挠度矩阵相乘所得，当边界条件及刚度矩阵已知时即可反推位移矩阵。最后，将结构的几何与物理方程相结合，得到结构的全部力学特性。

4 3种计算方法的对比分析

4.1 工程概况

以拟建设的一栋5 层钢混组合正六边形蜂窝型空腹夹层板楼盖空间盒式结构房屋为对象，该建筑为多层大跨度工业厂房，建筑内部需设置大空间，需要在建筑四周布置钢筋混凝土框架柱。该建筑结构安全设计等级为二级，建筑抗震设防为7 度，设计地震分组为第一组，场地类别为Ⅲ类。建筑底层层高6.0 m，标准层层高4.5 m。由于建筑内部不允许布置竖向框架柱，楼盖跨度较大，需采用适合大跨度的楼盖结构体系。钢混组合正六边形蜂窝型空腹夹层板空间盒式结构平面布置如图6所示。

图6 正六边形蜂窝型平面布置图（单位：mm）Fig.6 Layout plan of regular hexagon honeycomb type

钢混组合正六边形蜂窝型空腹夹层板空间盒式结构楼盖建筑平面由多个边长为2.0 m 的正六边形空间网格组成，建筑平面短跨方向尺寸为20.8 m，长跨方向尺寸为46.0 m。现浇钢筋混凝土框架柱沿建筑四周布置。在建筑短跨方向，正六边形网格楼盖与边梁组成等腰三角形，框架柱布置在边梁节点上，柱间间距为3.464 m；在建筑长跨方向，部分正六边形网格楼盖一部分即为边梁，另一部分与边梁组成梯形，框架柱布置在边梁节点上，柱间间距分别为4.0 m和2.0 m。

4.2 设计参数

空间盒式结构构件截面尺寸见表1。

表1 空间盒式结构构件截面尺寸Tab.1 Sectional dimensions of space box structure members单位：mm

4.3 有限单元法

运用大型有限元结构分析软件（ANSYS）对空间结构分析模型进行构建，主要分4 个基本环节：几何模型的建立、有限元模型的生成、加载及求解和结果的评估及分析。本节为3 种计算方法的对比分析，因此只建立底层空腹夹层板有限元模型。

采用2D 实体BEAM188 单元模拟上下肋钢梁、钢结构剪力键和建筑四周现浇混凝土框架柱；采用SHELL181 板单元模拟楼盖上表层混凝土薄板[14]。钢结构空腹夹层梁与建筑四周现浇混凝土柱的连接方式为公共节点刚接，空腹夹层板周边混凝土柱底节点施加沿3 个坐标轴位移为零和转角为零的边界条件[15]。各构件的参数见表2。结构分析模型楼面外荷载依据GB 50010—2010《建筑结构荷载规范》相关要求，建筑楼面恒荷载标准值为4.4 kN/m2，活载标准值为5.0 kN/m2；不上人屋面恒载标准值为4.4 kN/m2，活载标准值为0.5 kN/m2。有限元结构分析模型各层楼面输入均布荷载设计值为13.2 kN/m2，不上人屋面均布荷载设计值为6.5 kN/m2。

表2 空间盒式结构各构件材料参数Tab.2 Material parameters of components of space box structure

在有限元分析模型中，框架柱每层划分为一个单元；空腹夹层板楼盖六边形网格每边钢结构上肋梁、下肋梁划分为一个单元；六边形网格交点处连接上下肋梁的竖向构件剪力键划分为一个单元；上表面现浇混凝土楼板以形心为交点，沿六边形网格边划分为6 个正三角形板单元。正六边形蜂窝型空腹夹层板楼盖有限元模型如图7所示。

图7 正六边形蜂窝型空腹夹层板楼盖有限元模型Fig.7 Finite element model of hexagonal honeycomb open web sandwich panel floor

不考虑抗震墙对结构的影响，仅在结构模型第一层混凝土薄板上布置方向向下的均布面荷载13.2 kN/m2。位移云图如图8所示。

图8 正六边形蜂窝型空腹夹层板楼盖位移云图（单位：m）Fig.8 Displacement nephogram of hexagonal honeycomb openweb sandwich panel floor

4.4 实用计算方法

以抗弯刚度等效为原则将钢空腹楼盖等效为实腹H 型钢梁体系，得到蜂窝型实腹梁楼盖腹板厚度d1：

即实腹H 型钢梁的尺寸为Hh1×b1×d1×f1=1 000 mm×300 mm×11 mm×18 mm。用ANSYS 建立的等效钢实腹楼盖有限元模型及位移云图如图9 和图10 所示，其中钢实腹楼盖结构中，每个正六边形蜂窝型网格中钢实腹H 型梁划分为一个单元，上表面现浇混凝土楼板同样以形心为交点，沿六边形网格边划分为6 个正三角形板单元。楼盖模型除自重外，输入相同均布面荷载13.2 kN/m2。

图9 正六边形蜂窝型等效实腹楼盖有限元模型Fig.9 Finite element model of hexagonal honeycomb equivalent solid web floor

图10 正六边形蜂窝型等效实腹楼盖位移云图（单位：m）Fig.10 Displacement nephogram of hexagonal honeycomb equivalent solid web floor

4.5 拟夹层板法

根据第1 节式（48）编制MATLAB 计算程序，计算了各考察点挠度，考察点示意图如图11 所示。汇总了3 种方法得到的剪力键底部的挠度值，见表3。

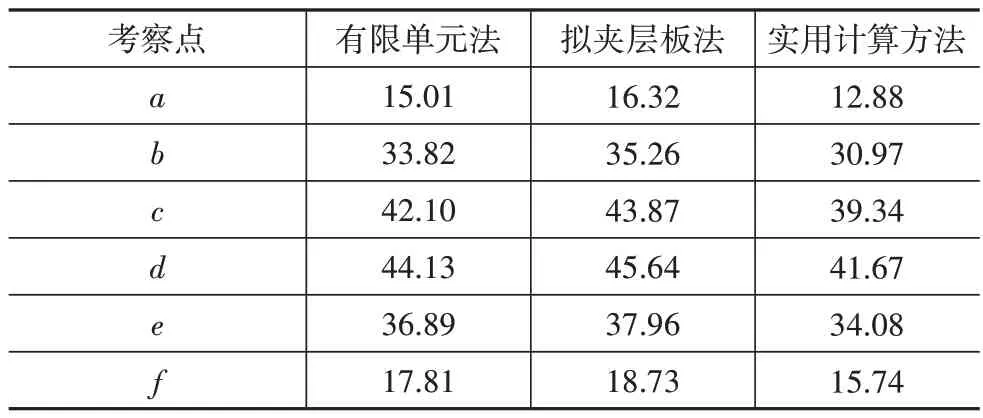
表3 工程算例楼盖挠度值Tab.3 Engineering calculation example floor deflection单位：mm

图11 正六边形蜂窝型空腹夹层板楼盖考察点示意图Fig.11 Schematic diagram of inspection points for hexagonal honeycomb open web sandwich plate floor

由图8、图10与表3可知，用有限单元法、实用计算法、拟夹层板法计算钢混组合正六边形蜂窝型空腹夹层板楼盖变形时，楼盖挠度的变化规律相同，均为中间大、两边小。对于楼盖中间测点的挠度，实用计算方法所得挠度值最小，为41.67 mm；拟夹层板法所得挠度值最大，为45.64 mm；实用计算方法与拟夹层板法在各点的挠度值最大误差为11.51%。3 种计算方法都满足工程精度的要求，因此3 种算法都可用于钢混组合正六边形蜂窝型空腹夹层板楼盖的变形计算。