面向粒子图像测速的光流金字塔插值优化方法

单良，简娟，熊俊哲，施飞杨，洪波，楼晓颖，孔明

（1 中国计量大学 信息工程学院 浙江省电磁波信息技术与计量检测重点实验室， 杭州 310018） （2 中国计量大学 计量测试工程学院，杭州 310018）

0 引言

人类的生产和生活处处离不开流场［1］。大气中的涡流以及管道、河流等地方的涡旋都是常见的流场之一。粒子图像测速法（Particle Image Velocimetry ，PIV）可以在不接触流场的情况下，对流场内的运动情况进行测量，广泛应用于图像分析和数字成像等领域。在不干扰流体运动的情况下［2］，为流体运动的定性描述以及定量研究提供相对理想的数据基础［3］。1984 年，ADRIAN R J 首次提出了粒子图像测速的概念［4］。在PIV 系统中，光流法是一种常见的算法，HORN B 和SCHUNCK B G 首次提出了光流算法［5］，其主要优点在于基于像素的差分特性，可以在每个像素（1 个矢量/1 个像素）上生成精细的速度矢量，这显著提高了流场的空间分辨率。此外，由于光流场是连续可微分的，这使得粒子在低速区域有更好的测量精度［6］。HORN B 和SCHUNCK B G 给出了光流亮度约束方程的模型方程，并使用该模型方程来构建目标函数［7］。但光流法也有一定的局限性，先前的误差分析表明，光流法的误差与像素强度的位移有关。平滑度约束决定了光流法比起大位移更适合恢复小位移的速度矢量。LIU T S 等［8］为了使光流法能在大位移上应用更广，提出了一种多尺度金字塔迭代光流法，但多尺度金字塔迭代光流法对初始估计敏感，初始估计的准确性对最终结果的影响较大。为了提升初始光流估计结果的准确性，LU J 等［9］提出了基于场分割的变分光流法，通过对光流场的全局优化，可以产生相对精确的光流估计结果。该方法对于刚性运动场景下的光流估计表现较好，但在非刚性运动和较大形变的场景中的适应性相对较弱。LIU T 等［10-11］提出了一种混合粒子图像测速法，该方法能够捕捉到非刚性运动中更准确的运动边界和细节，提供更准确的光流估计。在上述光流法中，为了准确地计算像素的运动，需要在相邻帧之间进行像素的对齐，这项工作通过图像插值技术来实现。

双线性插值法是多尺度金字塔迭代光流法中常见的插值方法，但是其重建角度精度不高且均方根误差较大。双线性插值得到的图像细节会因为斜率的不连续和平滑作用而变得模糊［12］，尤其在图像边缘附近失真和模糊会更严重。双三次插值也是一种常见的插值算法，可以在两个方向上进行三次插值，但这也意味着双三次插值具有更高的复杂性，限制了双三次算法的使用［13］。最近邻域插值法（Nearest Neighbor Interpolation，NNI）通过计算站点与不同格点之间的距离，把计算出来的最小距离格点的值赋值给站点［14］，通过在当前图像平面中搜索具有最相似梯度方向的最近像素来实现边角对应［15］。通过最近邻域插值法对图像进行扩展，可以保留原始边缘，降低图像边缘处的阶梯型失真效应和边缘模糊效应［16］。

本文在多尺度金字塔迭代光流算法的基础上，借鉴了最近邻域插值的思想，提出了一种面向粒子图像测速的光流金字塔插值优化方法。分别在单涡流、双涡流和DNS 湍流三个流场中使用本文所提算法进行仿真实验，并搭建实验所需的PIV 测量平台，最后通过实际的涡流场和射流场来验证本文算法的实际性能。

1 粒子图像测速原理与方法

1.1 PIV 原理

PIV 是一种利用粒子图像进行流体速度测量的技术，通过比较一定时间间隔内拍摄到的一对图像来计算流场中粒子的速度［17］。PIV 测量系统包括光源、准直透镜、CMOS 相机和样品池。实验系统示意图如图1所示。其实验系统原理为：白光源发出一束光，在准直透镜的作用下，该束白光变成一束平行光束，并照亮示踪粒子所在的样品池，CMOS 相机在一定时间间隔内对样品池中的粒子进行拍摄记录，将拍摄到两帧粒子图像放入PIV 系统中处理得到二维速度场矢量。

1.2 金字塔插值优化方法

光流是图像的表观运动，它传达了图像的变化［18］。光流法仅利用连续帧的相对运动信息即可获得结果，无需背景知识，不受复杂场景的影响［19］。

HORN B 和SCHUNCK B G 给出了光流亮度约束方程的模型方程

（x， y）是某一像素点的位置，I是图像亮度，该等式在时间间隔很短时适用。当dt趋于0 时，对等式左边使用一阶泰勒级数展开，展开结果如下：

式中，v和u分别代表垂直方向和水平方向的速度，Ix代表图像x方向的差分，Iy代表图像y方向的差分，It代表两幅图像的帧间差，为了更好的确定速度场，通常使用具有平滑度约束的变分公式，得到HS 变分光流法的优化目标函数，再利用Euler-Lagrange 方程求解最小化目标函数，得到光流的迭代方程［20］

假设，原始图像A的大小为R×C，缩放图像B的大小R'×C'，行缩放系数为Sr，列缩放系数为Sc。

B中的每个像素点（r'，c'），在A中的对应位置为（rf，cf），

A图像中最邻近的整数像素位置（r，c）

式中，（rˉ， cˉ）是分数像素位置，用于获得B（r'，c'）

本文共使用了两种不同的光流法，分别应用在速度场初始估计处（使用HS 光流法）和细化速度场处（DIOF 变分光流法）。算法框图如图2 所示，首先输入两帧拍摄到的粒子图像，再对两帧图像进行明暗校正，使其满足光流法的亮度一致特性，在得到初始速度场之前先对速度场使用HS 光流法进行初始估计，再对得到的初始速度场使用DIOF 光流算法进行细化，然后对细化后的速度场进行降采样，得到三层金字塔图像。在第一层金字塔图像中首先确定目标像素的位置，根据目标像素的位置来确定最邻近像素，再使用插值优化方法对金字塔图像求解的每一层速度场进行插值以得到更高分辨率的图像，从而得到更精确的速度场向量。

图2 面向粒子图像测速的光流金字塔插值优化方法Fig. 2 Basic block diagram of optical flow pyramid interpolation optimization for particle image velocimetry

2 仿真与分析

为了验证本文提出算法的正确性，在单涡流、双涡流、DNS 湍流三个流场中分别进行仿真实验。采用均方根误差（Root Mean Square Error， RMSE）和平均角度误差（Average Angular Error， AAE）对算法的性能进行评估，RMSE 和AAE 的评价指标的表达式分别如式（8）和（9）所示。

2.1 单涡流速度场重建

本文使用MATLAB 进行单涡流仿真实验。首先输入两幅时间间隔为1 s 的单涡流粒子图像，图像大小为256 pixel×256 pixel，经过HS 光流法获得初始速度场后，使用面向粒子图像测速的光流金字塔插值优化方法（以下简称OP+NNI）对图像进行插值重建，以获得精确速度场。此外，本文也对多尺度金字塔迭代光流法中常用的的双线性插值（以下简称OP+Biliner）进行了速度场重建，重建速度场结果如图3 所示。

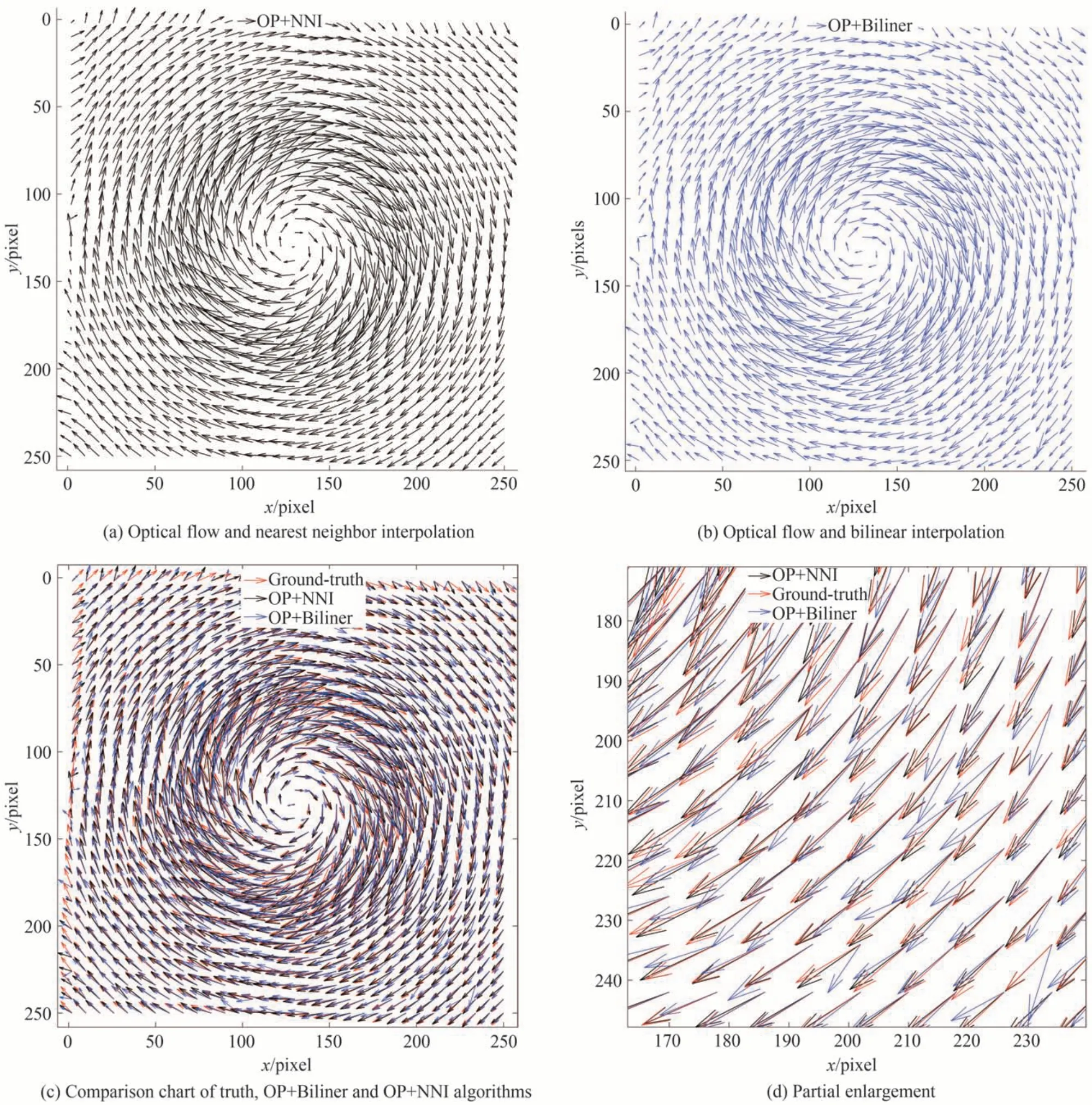
图3 单涡流速度场重建Fig. 3 Single-vortex velocity field reconstruction

其中，红色箭头为速度场真值，黑色箭头为OP+NNI 提出的方法所重建的速度矢量，蓝色箭头表示OP+Biliner 算法的重建结果。图3（d）是真值、OP+Biliner 和OP+NNI 提出方法的速度场重建局部放大对比图，从图3（d）中不难看出，在单涡流场中，本文所提算法优于OP+Biliner，尤其是在图像右下角边缘部分，本文提出算法的重建角度误差更小。

OP+Biliner 和OP+NNI 的重建误差如表1 所示。经计算得，OP+NNI 的均方根误差比OP+Biliner 降低了15.96%，平均角度误差比OP+Biliner 降低了19.87%。

表1 单涡流场的重建精度Table 1 The reconstruction accuracy of single vortex

2.2 双涡流速度场重建

为了进一步验证本文提出算法的正确性，本文进行了双涡流仿真实验。首先输入两幅双涡流图片，涡旋中心直径为60 pixel，涡旋1 的中心坐标为（80，100），涡旋2 的中心坐标为（150，100）。然后分别对OP+NNI、OP+Biliner 进行速度场重建，重建结果如图4 所示。

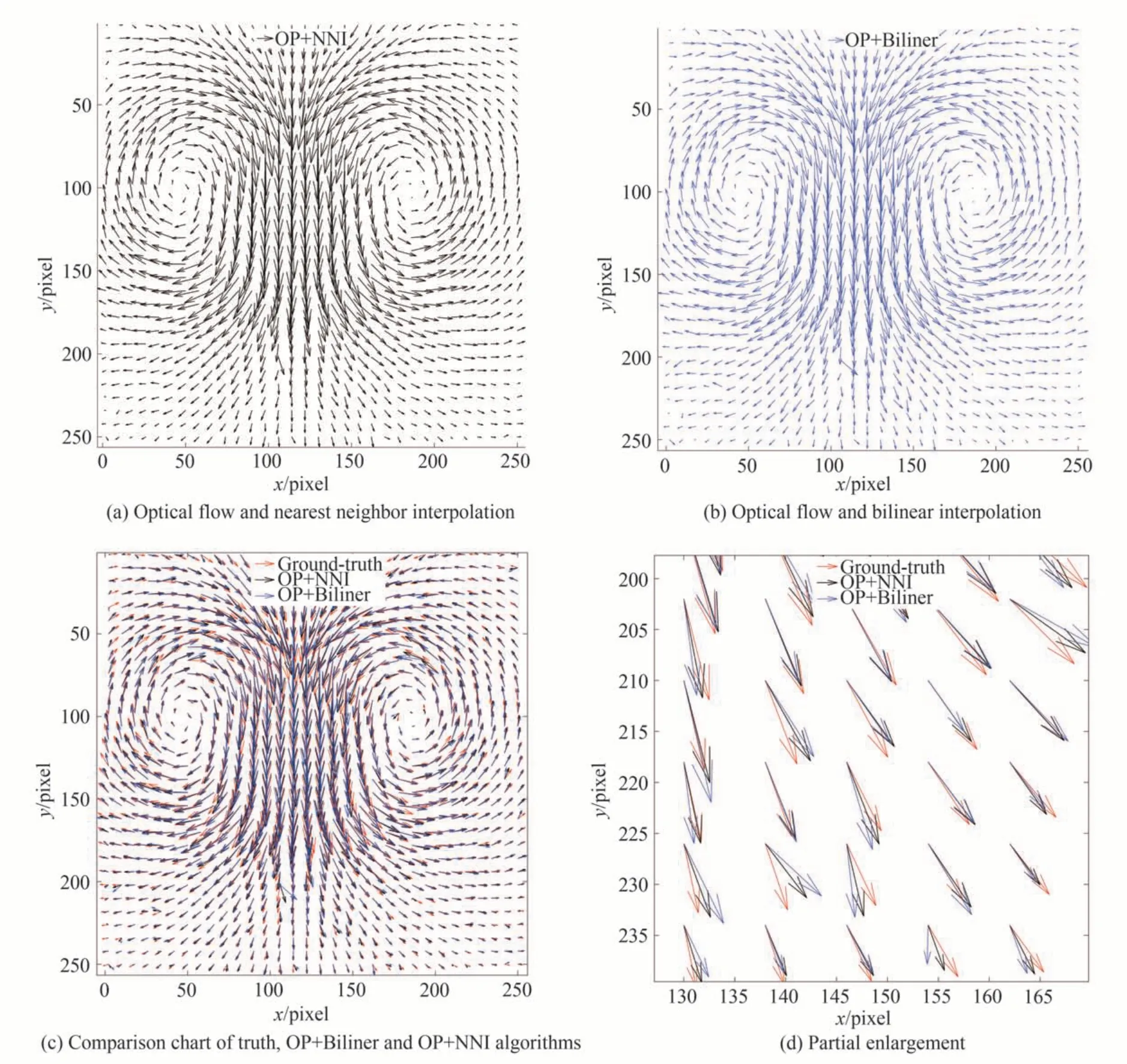
图4 双涡流速度场重建Fig. 4 Pair vortex velocity field reconstruction

其中，红色箭头为速度场真值，黑色箭头为OP+NNI 重建的速度矢量，蓝色箭头表示OP+Biliner 算法的重建结果。图4（d）是真值、OP+Biliner 和OP+NNI 的速度场重建局部放大对比图，从图中可以直观地看出，在双涡流场中，OP+NNI 重建的速度场与真值更接近，尤其是在图像下边缘中间部分，本文提出算法的重建角度误差更小。

OP+Biliner 和OP+NNI 的重建误差如表2 所示。经计算得，OP+NNI 的均方根误差比OP+Biliner 降低了15.03%，平均角度误差比OP+Biliner 降低了19.56%。

表2 双涡流场的重建精度Table 2 The reconstruction accuracy of pair vortex

2.3 DNS 湍流速度场重建

除了涡流场，本文还进行了DNS 湍流仿真实验。输入两幅256 pixel×256 pixel 的DNS 湍流图像，分别对OP+NNI、OP+Biliner 进行速度场重建，重建结果如图5 所示。

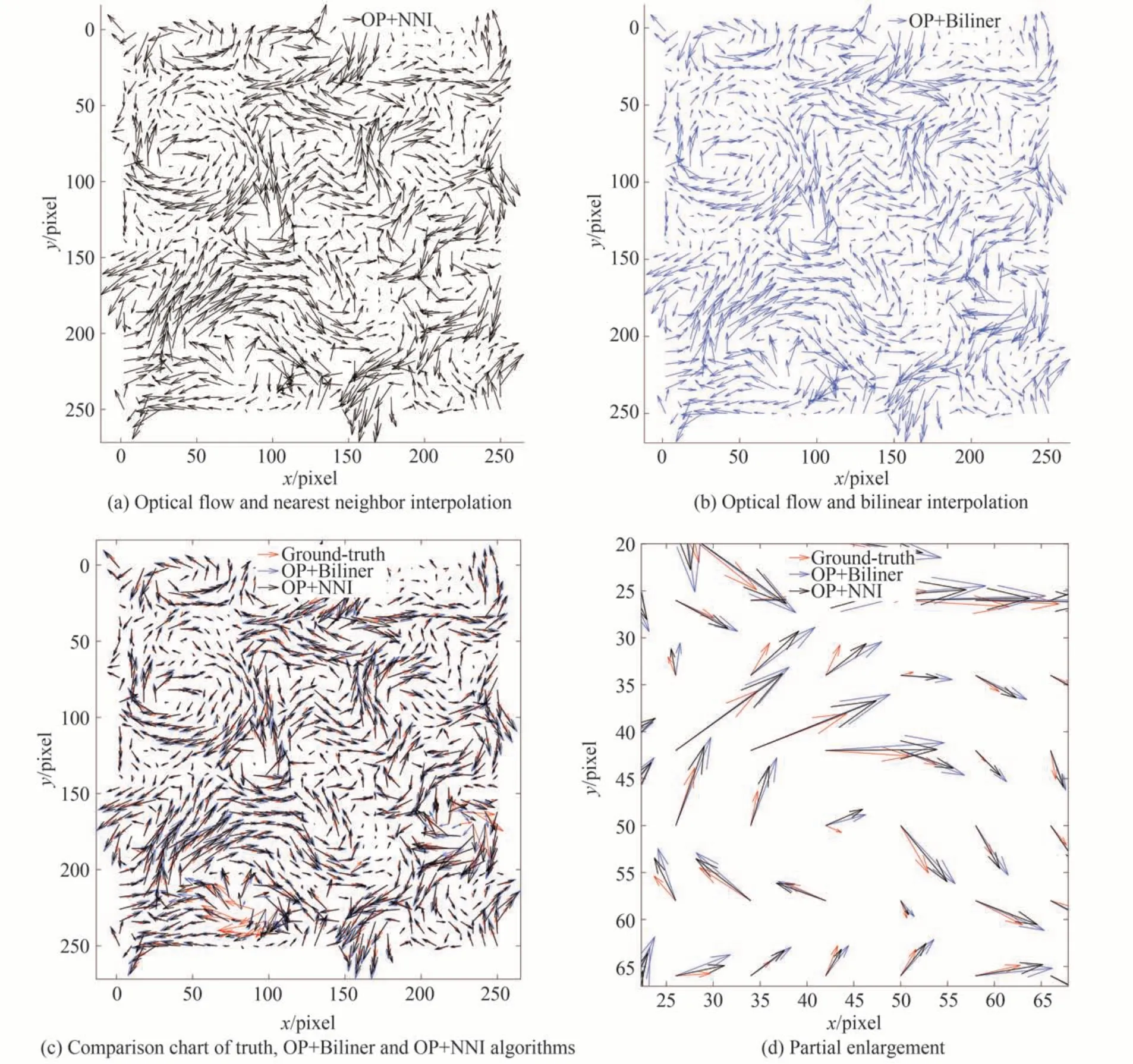
图5 DNS 速度场重建Fig. 5 DNS turbulence velocity field reconstruction

其中，红色箭头为速度场真值，黑色箭头为OP+NNI 所重建的速度矢量，蓝色箭头表示OP+Biliner 算法的重建结果。在图5（c）中，我们观察到在x 轴50 到100 区间内，OP+Biliner 和OP+NNI 的误差都比较大，这是因为此时粒子处于不稳定的对流状态下，而粒子在不稳定的对流状态下会产生相对较高的误差［21］。图5（d）是真值、OP+Biliner 和OP+NNI 的速度场重建局部放大对比图，从图中可以直观地看出，在DNS 湍流场中，OP+NNI 重建的速度场与真值更接近，尤其是在图像左上角边缘部分，本文提出算法的重建角度误差更小。

OP+Biliner 和OP+NNI 的重建误差如表3 所示。经计算得，OP+NNI 的均方根误差比OP+Biliner 降低了14.09%，平均角度误差比OP+Biliner 降低了17.37%。

表3 DNS 湍流的重建精度Table 3 The reconstruction accuracy of DNS turbulence

2.4 位移参数对重建结果的影响

在PIV 测量系统中，速度场精度会受一些因素的影响，其中包括示踪粒子的粒径和示踪粒子在流场中运动的位移。可以在仿真实验中调整这两个参数的大小，以便系统的评估这两个参数对重建结果的影响。

首先对示踪粒子在流场中运动的位移大小进行调整。在MATLAB 里的PIVLab 工具包中，生成一个256 px×256 px 的平面，并在该平面内随机生成5×104个示踪粒子，示踪粒子的粒径设为4 px，并将流场的（128，128）处设为流场中心，由于实验中不可避免的会有噪声的存在，因此，本文还设置了1×10-3的随机噪声，粒子位移分别取1～7 px，位移小于等于5 px 为小位移，位移大于5 px 为大位移。将两种算法得到的速度场重建结果进行对比，如图6 所示。

图6 位移大小对精度的影响Fig. 6 Influence of displacement on accuracy

图6 表示了两种算法在经过400 次迭代后示踪粒子的位移与均方根误差和平均角度误差之间的关系，其中横轴为最大位移，图6（a）纵轴为均方根误差大小，图6（b）纵轴为平均角度误差大小。

图6 表明：1）由图6（a）可以看出，粒子运动位移越大，三种流场的均方根误差也越大。但OP+NNI 的算法始终优于OP+Biliner。在小位移情况下，RMSE 精度最高可以提高18%左右，当粒子位移较大时，本文算法的RMSE 精度最高仍比OP+Biliner 提高15%左右。2）随着粒子运动最大位移的增大，本文提出算法的AAE 始终比OP+Biliner 更低，且OP+NNI 的角度误差精度可以比OP+Biliner 提高20%左右。且由图6（b）可以看出，5 px 处是位移大小与平均角度误差关系曲线的拐点，此后两种算法的角度误差均逐渐变大，这是因为光流法更适合粒子的小位移运动，当粒子移动的位移较大时，光流法便不再适用。但本文算法的重建精度依然优于OP+Biliner。

2.5 粒径参数对重建结果的影响

其次对示踪粒子粒径大小进行调整。依然在MATLAB 里的PIVLab 工具包中，生成一个256 px×256 px的平面，并在该平面内随机生成5×104个示踪粒子，并模拟了1～7 px 七种不同粒径下的三种流场，将两种算法得到的速度场重建结果进行对比，如图7 所示。

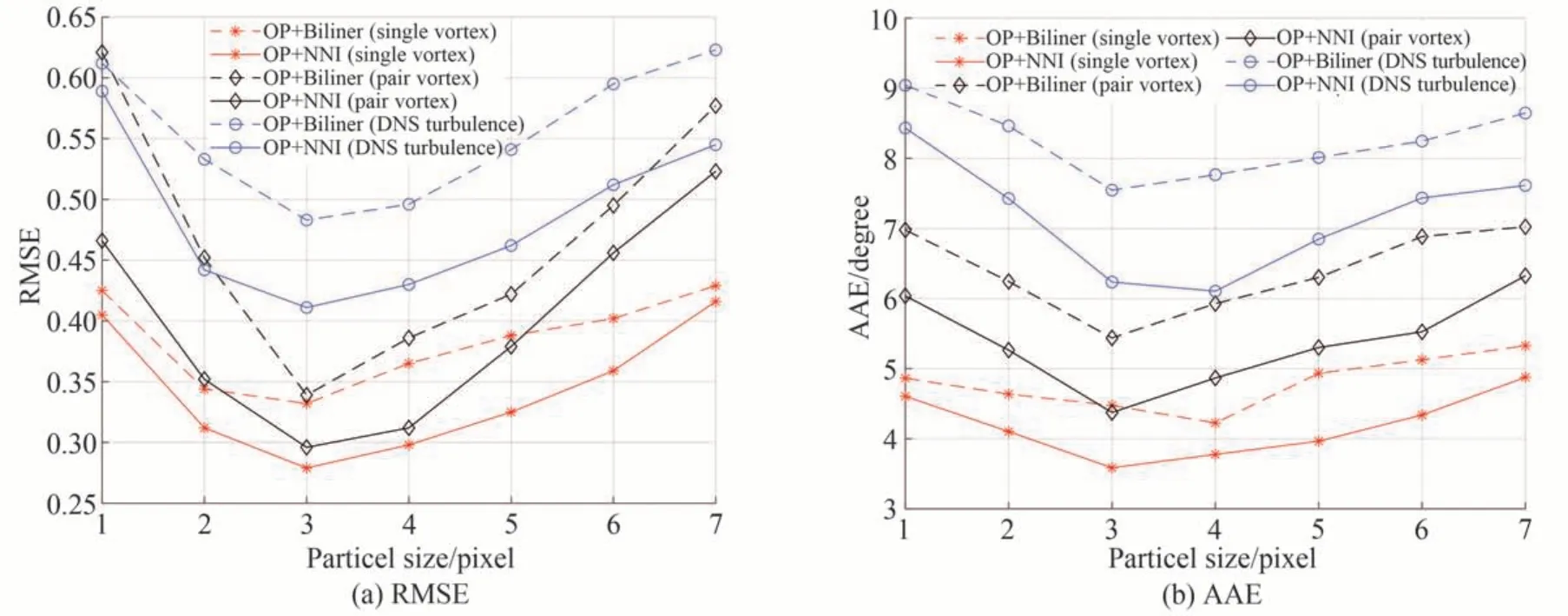
图7 粒径对重建误差的影响Fig. 7 Influence of particle size on reconstruction error

图7 表示了两种算法在经过400 次迭代后示踪粒子的位移与均方根误差和平均角度误差之间的关系，其中横轴为粒径大小，图7（a）纵轴为均方根误差大小，图7（b）图纵轴为平均角度误差大小。

结果显示，在粒径大小为1～7 pixel 的情况下，OP+NNI 的RMSE 和AAE 均优于OP+Biliner，从图7（a）、图7（b）中可以看出，当粒子粒径为3px 时，两种误差都达到最小，此后两种误差均开始增加，这是因为当粒径过大时，粒子可能会在平面内产生重叠，导致误差变大。总体来看，本文提出的方法相对于OP+Biliner 对速度场重建的效果更好。

3 实验与分析

本文搭建的PIV 实验系统如图8 所示。首先将二甲基硅油加入在85 mm×85 mm×50 mm 的石英样品池中，并里面加入一定量的示踪粒子作为待测流场。然后保证实验在黑暗环境下进行，其中白光源SLS301发出非相干白光，光阑将白光控制在适合待测流场的范围内，再通过电动滑台来控制样品池的平移或旋转，来模拟仿真实验中的平流场或涡流场，使用FLR Blackfly 的BFS-U3-51S5 型号的CMOS 相机来拍摄待测流场，在将拍摄到的粒子图像送入PC 进行处理，最终得到二维PIV 速度场。

图8 PIV 测量实验平台Fig. 8 PIV measurement experimental platform

使用电动滑台分别对待测流场进行旋转来模拟涡流场、人为的对待测流场注水来模拟射流场，并对实验数据进行验证。

3.1 旋转实验

由于二甲基硅油粘度高、稳定性强，在实验中能更好的反映示踪粒子的运动轨迹，故本实验选择在样品池中加入二甲基硅油来作为待测流场的试剂，并在样品池中加入100 μm 的PSP 粒子。实际实验中的旋转流场通过电动滑台的旋转来实现，将CMOS 相机置于样品池正上方，在1 s 时间间隔内连续拍摄两帧粒子图像，为了避免由于反光造成的干扰，我们选择了相机视场中心256 px×256 px 区域的粒子进行速度场重建，采集到的两帧粒子图像如图9 所示。

图9 旋转实验采集的粒子图像Fig. 9 Particle images collected by rotation experiment

两个时刻内重建的速度场图像如图10 所示，其中图10（a）为OP+Biliner 重建结果，图10（b）为本文提出算法重建结果。

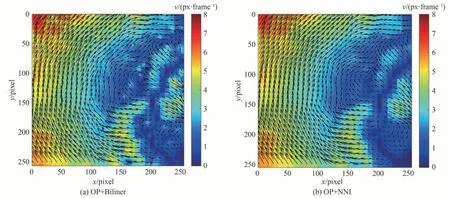
图10 旋转实验的估计速度场Fig. 10 The estimated velocity field of rotation experiment

两种算法重建的速度场矢量在流形表现形式上基本相似，为了更好地看出差别，我们计算了流场内所有点的角度误差，并在x轴随机选取一列像素点（本文选取的是60 px 处对应的256 个像素点），并画出这256 个像素点对应的平均角度误差，绘制折线图如图11 所示。

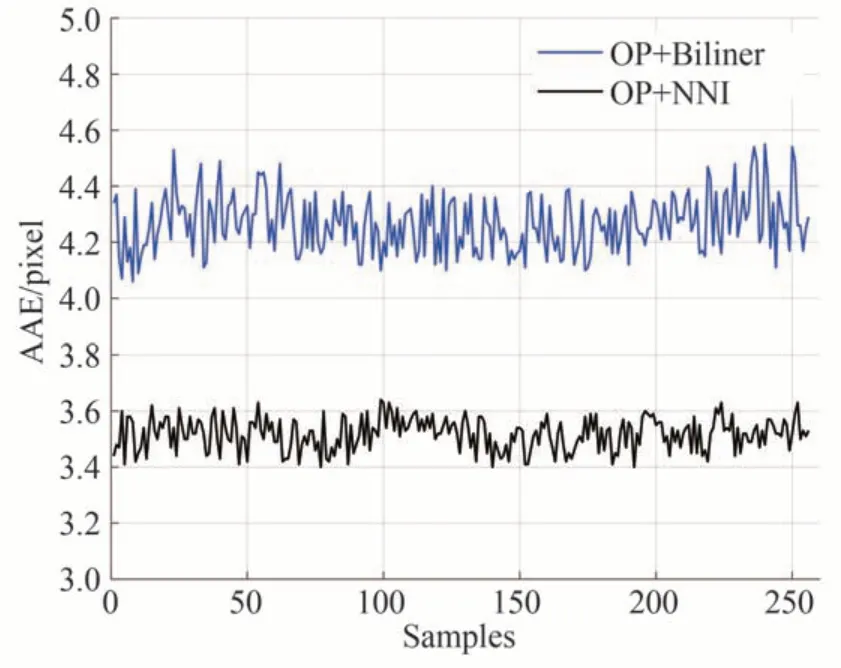
图11 旋转实验任意一像素点的重建角度误差分布Fig. 11 Distribution of reconstruction angle error for any pixel point of the rotation experiment

从图11 可以看出，本文提出的算法计算得到的平均角度误差基本集中在3.4～3.6 pixel 之间，比OP+Biliner 算法降低了约25%，且误差振幅小，算法更稳定。

3.2 注水实验

为了更好地验证所提算法的实用性，除了旋转实验，本节还进行了注水实验。与旋转流场不同的是，注水实验中我们选择注射器来注水，并将CMOS 相机置于样品池右侧来拍摄待测流场，时间间隔仍为1 s，拍摄的两帧粒子图像如图12 所示。

图12 注水实验采集的粒子图像Fig. 12 Particle image captured by water injection experiment

两个时刻内重建的速度场图像如图13 所示。其中图13（a）为OP+Biliner 重建结果，图13（b）为本文提出算法重建结果。

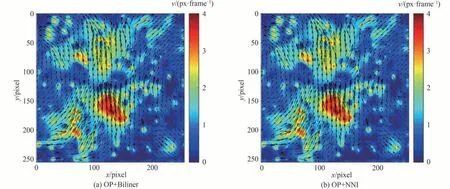
图13 注水实验的估计速度场Fig. 13 The estimated velocity field of water injection experiment

两种算法重建的速度场矢量在流形表现形式上基本相似，为了更好地看出差别，我们再次计算了流场内所有点的角度误差，并在x轴随机选取一列像素点（本文选取的是60 pixel 处对应的256 个像素点），并画出这256 个像素点对应的平均角度误差，绘制折线图如图14 所示。

图14 注水实验任意一像素点的重建角度误差分布Fig. 14 Distribution of reconstruction angle errors for any pixel point of the water injection experiment

从图中可以看出，本文提出的算法计算得到的平均角度误差基本集中在4.1～4.4 pixel 之间，比OP+Biliner 算法降低了约20%，且误差振幅小，算法更稳定。

综合以上两个实验，可以验证本文提出算法的正确性，也说明本文算法在复杂流场中具有一定的实用性。

4 结论

本文提出了一种面向粒子图像测速的光流金字塔插值优化方法，用于减小重建误差，提升速度场精度。分别进行了单涡流、双涡流、DNS 湍流仿真实验，并与OP+Biliner 算法的重建结果进行对比，结果显示本文所提算法的RMSE 和AAE 至少比OP+Biliner 算法降低了15.96%和19.87%。此外，为了更好地探究速度场重建结果的影响因素，本文分别分析了示踪粒子的粒径大小和示踪粒子运动的最大位移对重建精度的影响，分析表明，无论在哪种粒径、哪种位移情况下，本文算法均优于OP+Biliner 算法，具体表现为RMSE 精度提高了18%左右，AAE 精度提高20%左右。在真实实验中，本文搭建了实验所需平台，且在该平台上进行了旋转实验和注水实验来验证本文算法的正确性和实用性，实验表明，两种算法重建的速度场流形基本一致，这表明了本文算法的正确性，以及在真实实验中具有一定的实用性。