基于机器学习和遗传算法的非局部晶体塑性模型参数识别1)
2024-04-15熊宇凯储节磊阚前华康国政
周 瑞 熊宇凯 储节磊 阚前华 康国政 张 旭 ,2)
* (西南交通大学力学与航空航天学院,应用力学与结构安全四川省重点实验室,成都 610031)
† (西南交通大学计算机与人工智能学院,成都 610031)
引言
晶体塑性有限元方法基于材料在离散滑移系的塑性滑移来研究单晶和多晶材料的塑性变形行为[1].由于在微米尺度下,材料非均匀变形相关的应变梯度效应不可忽略,需要建立可描述几何必需位错(geometrically necessary dislocations,GND)对力学行为的影响的非局部晶体塑性本构模型[2-5].非局部晶体塑性模型考虑的位错机制较多,描述位错行为的本构模型参数较多.合适的材料参数是晶体塑性模型拥有良好预测能力的先决条件,如何准确确定非局部晶体塑性本构模型的参数极具挑战.
传统的本构模型参数的确定方法采用的是“试错法”,即通过调整材料参数,直至模拟结果与实验结果或参考数据相匹配[6-7].在参数较少且参数影响较为明显的情况下,通过试错法是易于得到晶体塑性参数的.但是对于具有大量参数,且参数间可能会存在非线性作用的复杂本构模型,通过“试错法”调控参数极为困难.基于梯度的优化方法常常用于求解逆问题,已有学者借助优化算法确定本构模型参数[8-9].Mahnken 等[10]基于梯度的优化方法识别黏塑性材料本构模型的参数,但整个优化过程的收敛性和收敛速度极大地依赖于初始点的选取,仍无法避免不断的试错.相比之下,遗传算法(genetic algorithm,GA)采用了进化程序和交叉重组算法,并不需要有关目标函数的梯度信息.因此,有的学者考虑通过遗传算法确定本构模型参数[11-13].Savage 等[14]基于遗传算法,结合了微观结构数据与应力数据,成功识别了本构模型参数.Frydrych 等[15]基于压痕实验数据,通过将遗传算法的结果带入有限元方法中进行模拟,识别了晶体塑性模型的参数.然而遗传算法每次迭代都需要执行一次有限元模拟,提取输出结果,并通过与实验数据比较计算出适应度.晶体塑性有限元的模拟计算成本过高,会导致整个优化流程效率低下.因此,遗传算法是一种更为稳健的优化算法[16],可成功用于参数的识别,但是这种收敛的稳定性是以牺牲效率为代价的[17].
这里本文引入了机器学习方法来避免实际模拟计算成本过高的问题.机器学习模型的计算速度,远快于有限元的模拟过程,并且将机器学习模型用于替代模型的技术已经比较成熟,许多学者将其用于替代本构模型[18-19],用于建立参数到应力响应的映射.此外,已有学者将机器学习算法与本构模型计算过程相结合,通过机器学习算法加速有限元的计算.Heider 等[20]在回退-映射算法中加入了机器学习模型,加速了各向异性与非弹性材料响应的本构模型的计算过程.Wen 等[19]使用梯度提升树建立模型,当输入等效应力、等效应变、温度和等效应变率时,可以直接预测出塑性应变率和应变硬化模量.他们将这个模型加入有限元计算过程中,实现了计算的加速.其次,已有学者将机器学习方法用于识别晶体塑性模型的参数[21].例如,Veasna 等[22]结合Pareto最优点和机器学习方法,建立了多目标的优化模型,该模型能够有效确定晶体塑性本构参数.然而,结合机器学习和遗传算法进行非局部晶体塑性本构模型参数确定的研究还未见报道.
本文基于非局部晶体塑性本构模型,借助DAMASK平台[23]生成镍基高温合金的含孔洞模型单轴拉伸模拟数据,进而建立从参数到应力响应的机器学习模型.在此基础上,将机器学习模型与遗传算法进行耦合,通过已有实验数据,确定镍基高温合金的非局部晶体塑性模型参数.最后通过SHAP 工具,分析参数变化的影响.
1 模型与方法
对于简单的本构模型,可以通过机器学习从应力-应变曲线得到参数.但复杂的本构模型不满足一一对应关系,一条应力-应变曲线可能对应多组参数,所以难以直接确定本构参数.因此,本文采用了一种新颖的耦合机器学习模型的遗传算法进行参数优化,能够有效地规避上述问题.本文采用的算法流程分为3 个阶段:第1 阶段调控非局部晶体塑性模型的参数,通过晶体塑性有限元模拟生成大量数据;第2 阶段是根据已生成的数据,建立3 种不同的机器学习模型;第3 阶段是将机器学习模型与遗传算法相结合,通过不断的优化迭代获取最优参数.整个优化过程的流程图如图1 所示.

图1 参数确定优化过程流程图Fig.1 Flowchart of the optimization procedure for constitutive parameters
1.1 非局部晶体塑性本构模型
本文所采用的本构模型为基于位错机制的非局部晶体塑性模型,该模型考虑了金属材料变形过程中多种位错的力学行为.在有限变形框架下,变形梯度F可以通过乘法分解为弹性变形梯度Fe和塑性变形梯度Fp
式中,Fe描述晶格弹性变形,而Fp则描述由位错滑移引起的塑性变形.塑性变形梯度的演化率可以表示为
式中,Lp是位错运动引起的塑性速度梯度,可以表示为
位错运动时会遇到障碍,其平均速度vα可表示为
其中,cat为原子浓度,vT为黏滞速度,其可以表示为,η为黏滞系数,tS和tP分别表示位错克服Peierls 障碍和固溶原子障碍需要的时间.位错在障碍前的等待时间与位错尝试跨越障碍的频率和其成功跨越障碍的概率相关[25],可以表达为
其中,f为位错尝试跨越障碍的频率,幂指数项为位错成功跨越障碍的概率,kB为玻尔兹曼常数,τS和τP分别为固溶原子障碍和Peierls 障碍的强度,dobst为固溶原子直径,wk为双扭折宽度,p和q为描述障碍能垒的系数,τeff为滑移面上的有效分切应力,其可以表示为 α 滑移系上驱动力 τα与位错运动需要克服的林位错交互作用力 τcr之差
位错之间的相互作用力 τcr可以表示为
其中,G是剪切模量,为滑移系之间位错的相互作用强度系数.
位错的增殖、湮灭以及位错极性(单个位错与位错偶)的转变对材料的力学行为有重要的影响.假定不同类型位错的增殖率相同,则位错增殖率可以描述为
位错偶的湮灭类型有两种:其一为攀移造成的刃型位错偶湮灭,刃型位错偶的演化率可以表示为
对于非局部模型,关键在于考虑了位错流动,即位错信息在材料点之间的交换.滑移系 α 上的位错流量可以定义为可动位错密度和其运动速度的乘积,即fα=ραvα.由材料点的位错信息交换,可以给出位错密度的演化[25]
位错的流动通过穿透因子χ控制.使用有限体积离散的方法,位错流入邻近体积单元可以表示为
其中,V是体元体积,an为对应的面法向矢量,An为编号为n的面元面积.
1.2 遗传算法模型
遗传算法作为一种直接搜索方法,其优化结果通常会得到全局的最优值而不是局部最优值[26].遗传算法中的部分概念定义如下:
(1) 基因是评价公式中的可调参数,即所选取的非局部晶体塑性模型参数.
(2) 染色体表示个体的所有基因集合,即多个本构参数的集合.染色体代表单独个体,即一组本构参数.
(3) 种群表示染色体的集合,即多组非局部晶体塑性模型参数的集合.
(4) 适应度是对应于评价公式得到的数值,适应度越大表明染色体对应的评价结果越优.
(5) 选择阶段是根据适应度得到染色体被保留的概率,然后淘汰适应度低的个体.
(6) 交叉遗传表示种群中两个染色体间有概率发生基因互换.
(7) 变异表示染色体的基因可能发生随机变化.
本文将应力-应变曲线中的屈服应力和最终应力作为评价指标,通过确定二者的值即可确定应力-应变曲线.本文最大模拟应变为0.1,最终应力表示的是应变为0.1 时的应力.二者的值可以通过机器学习模型得到.本文依据常用的L2范数[27],建立了对应的评价公式评估适应度
其中,Dobj为评价值,和 σN分别对应机器学习计算和实验得到的应变为0.1 处的应力值,和 σ0分别对应机器学习计算得到的屈服应力和实验得到的屈服应力.评价值描述了屈服应力和最终应力与实验值的最大差值,当评价值最小时说明计算结果与实验值最为接近.个体的适应度为Fobj=Dm-Dobj,其中Dm表示每代中Dobj的最大值,此时适应度越大,对应的评价值越小.
本文采用的遗传算法程序流程主要包含两个阶段,第1 个阶段是确定非局部晶体塑性模型参数并且随机生成种群染色体,即随机化初始参数.第2 阶段主要是种群演化过程,首先通过机器学习模型计算种群中每个染色体对应的评价值,然后根据评价值得到适应度.此时种群中的最优值若是满足精度要求即可停止演化,若不满足则进入选择阶段.选择阶段将根据适应度淘汰部分个体,并将剩余个体依次进行交叉遗传和变异,最终得到新一代种群.然后计算新种群的适应度,反复迭代直至满足要求,如图2所示.
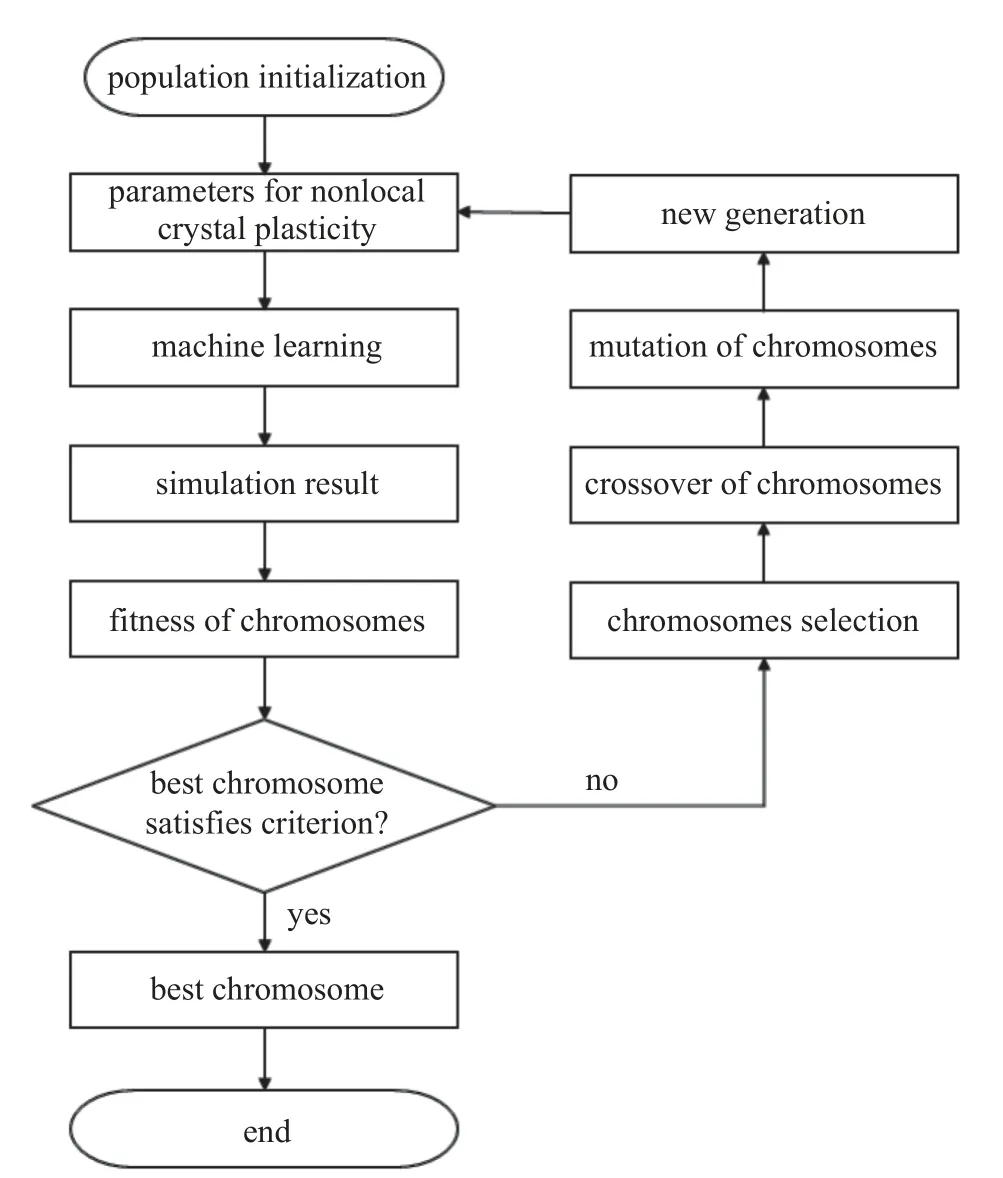
图2 非局部晶体塑性本构模型参数确定的遗传算法流程示意图Fig.2 Flowchart of genetic algorithm for determing the parameters of nonlocal crystal plasticity model
1.3 可解释机器学习模型SHAP
本文采用的可解释的机器学习模型来自Lundberg等[28]提出的SHAP 模型.SHAP 源于博弈论,是一种解释机器学习模型预测的方法.SHAP 是一种加性特征属性方法,即其模型的输出是输入变量的线性叠加[29].每个特征的贡献通过Shapley 值[30]表示,因此可解释模型g(x′) 可以表示为
其中,x′是从原始数据集x简化得到的输入特征,M是数据集中的特征数量,φ0是一个常数,φi是每个特征i对应的权重.
2 参数优化过程
2.1 非局部晶体塑性模型参数选择
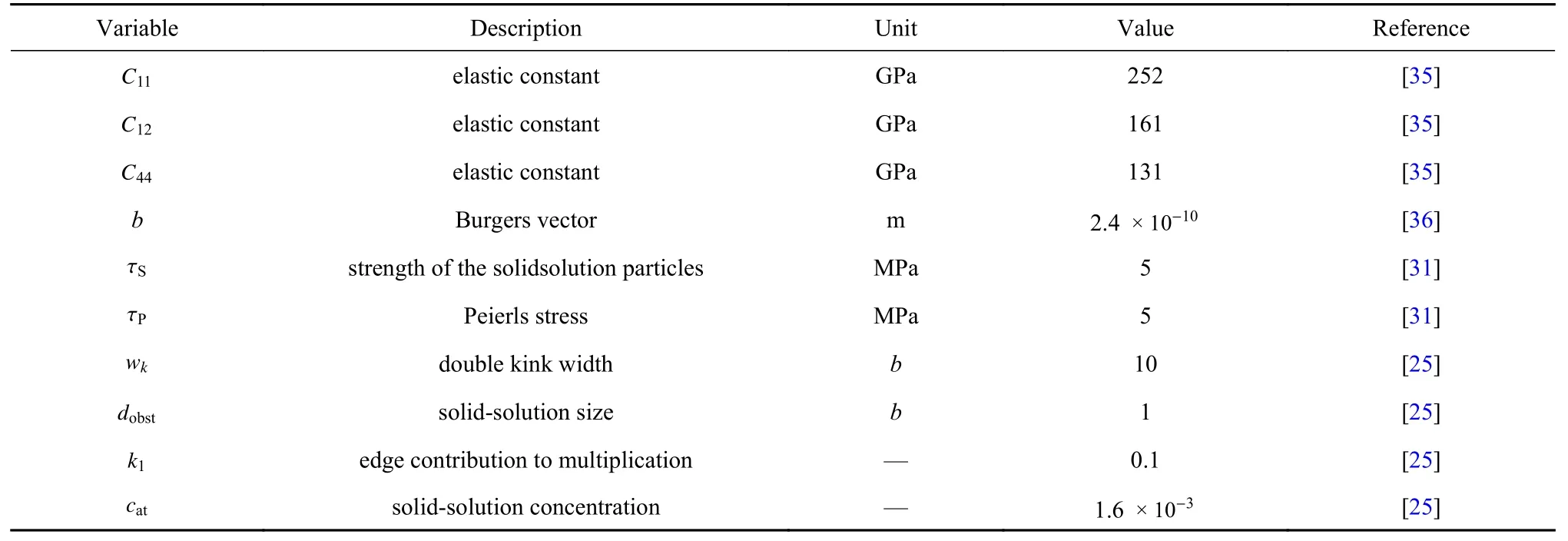
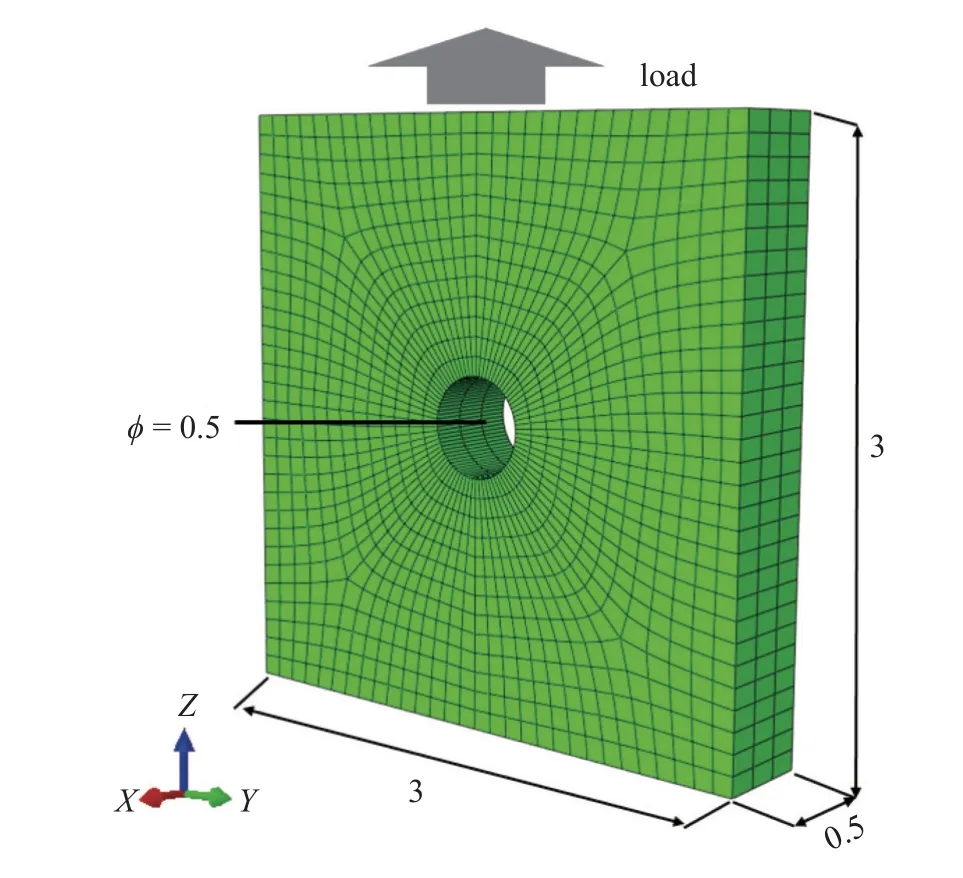
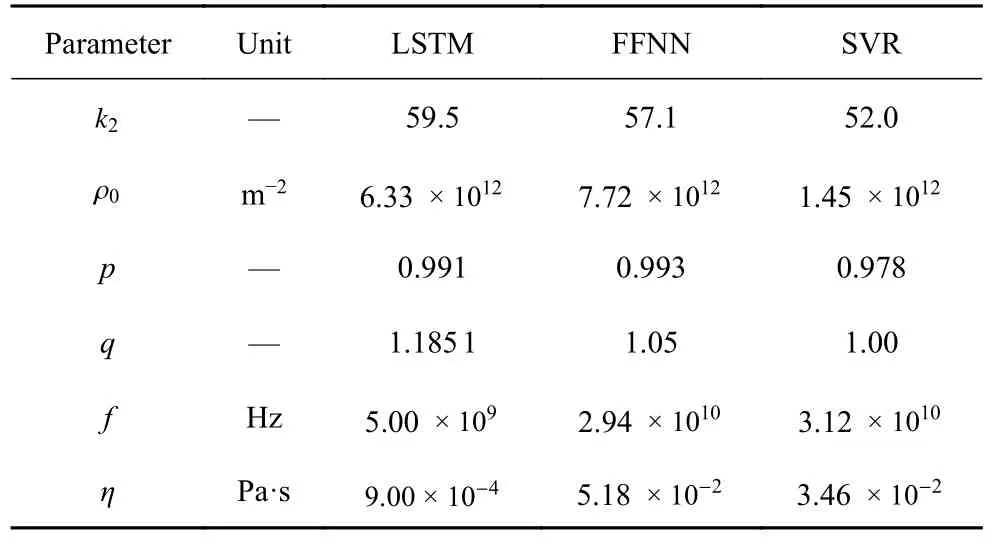
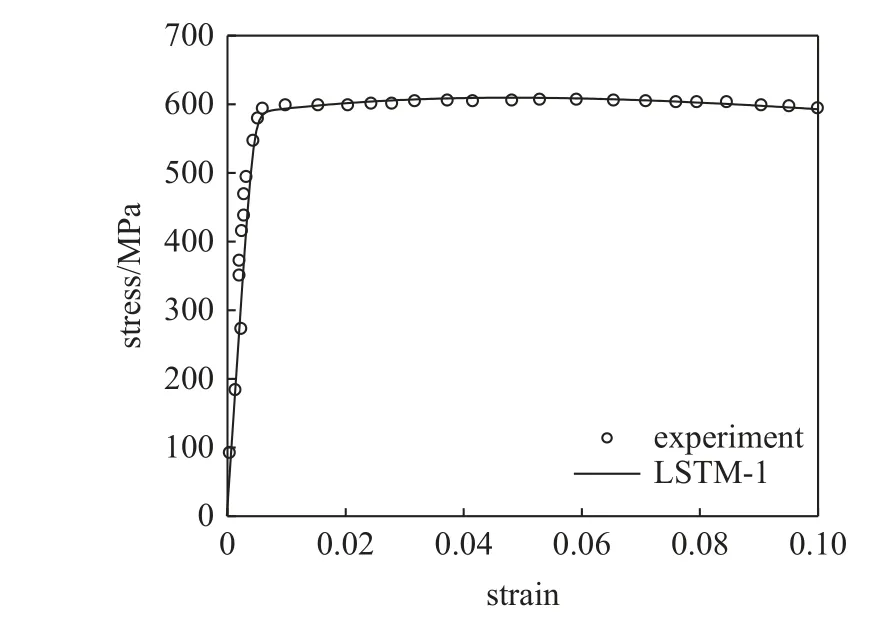
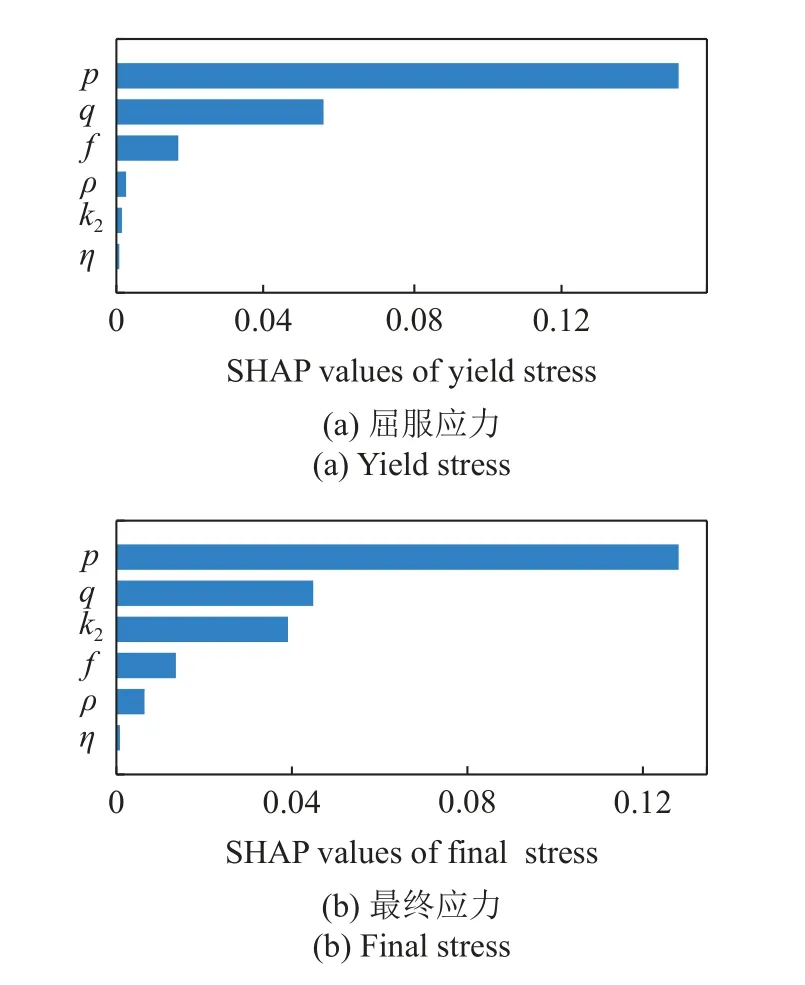
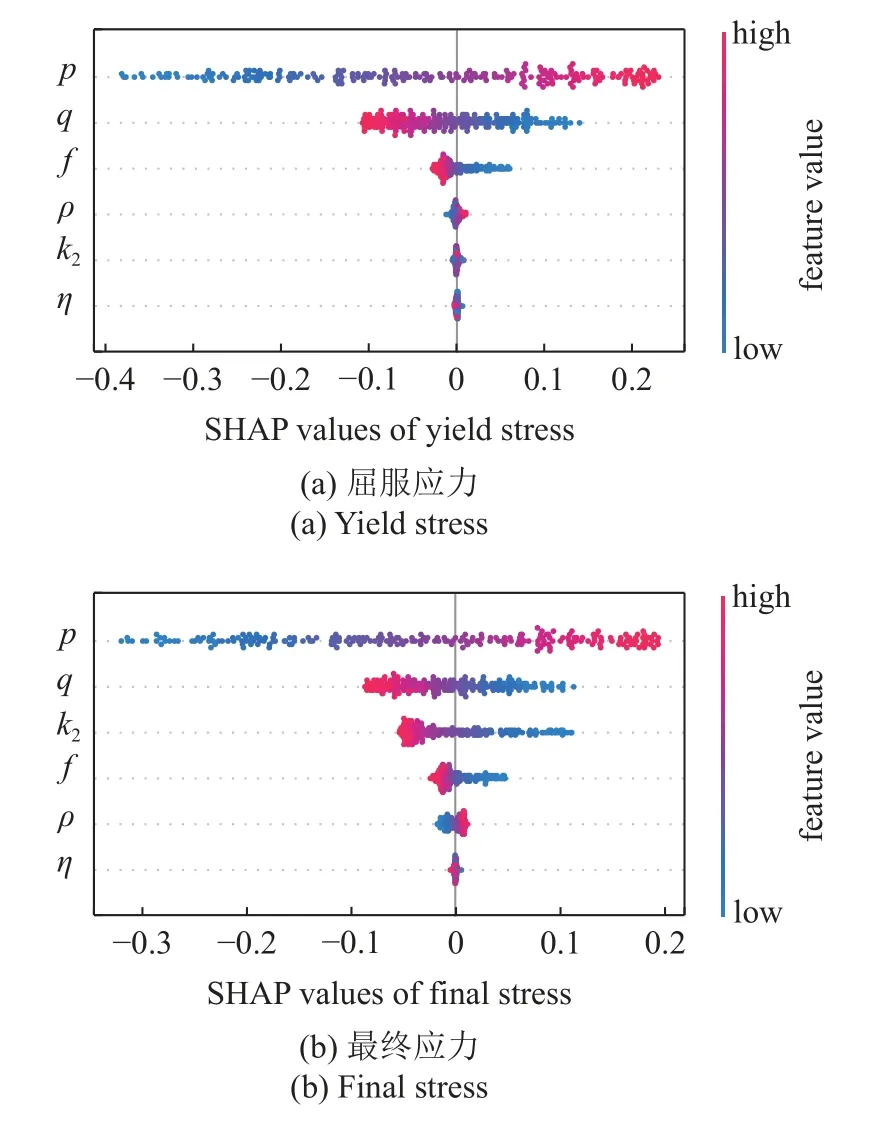
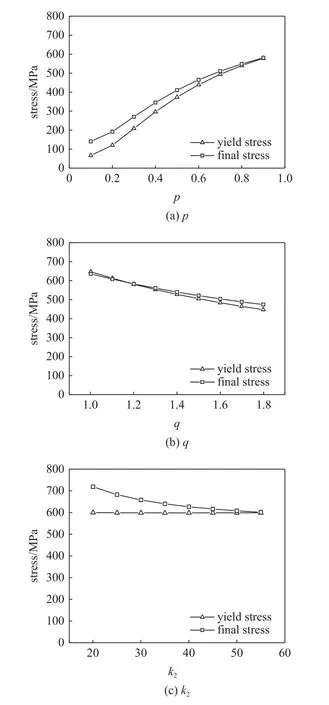
本文以镍基高温单晶合金作为研究材料.非局部晶体塑性模型中参数众多,大部分参数可以通过实验曲线或者材料本征的物理特性来确定,如弹性模型、泊松比以及位错Burgers 矢量大小等.因此,仅仅与塑性变形相关的本构参数,特别是与位错密度演化有关的模型参数被选为待拟合参数.待拟合参数会在一定范围内变化,它们的大小变化和组合在很大程度上影响了位错演化和塑性屈服与流动行为.参数的范围参考了文献中给出的镍基高温合金参数取值[31-33].其次在选择上下限时需满足相应理论要求,如p和q的取值需分别满足 0 表1 待拟合的晶体塑性模型参数Table 1 Unfit crystal plasticity parameter 表2 镍基高温合金的非局部晶体塑性模型参数Table 2 Nonlocal crystal plasticity parameter for Ni-based superalloys 本文的优化过程以镍基高温合金实验应力-应变曲线的屈服应力和最终应力作为目标结果,其数据源于参考文献[37].为体现非局部晶体塑性本构的特点,选取了含孔洞模型进行单轴拉伸模拟.在训练机器学习模型前,需获得足够的数据.因此,本文依据实验中的试样尺寸,建立了大小为0.5 mm×3 mm×3 mm 的晶体塑性模型,其包含有直径为0.5 mm 的穿透孔.模型以晶粒取向[001]作为拉伸方向,单元数量为2880,单元类型为C3D8R,如图3 所示.模型约束了x-y平面x和y方向的位移,并在x-y面施加沿z轴的应变控制载荷,应变率为1.0×10-4s-1,拉伸位移为0.3,因此最终应变为10%.根据建立的晶体塑性模型,在已确定的参数范围内,随机调整参数,并提交计算.最后进行后处理,每组数据取200 个应力-应变点组成应力-应变曲线,并提取相应的屈服应力和最终应力.将以上过程重复多次,完成数据生成,共生成1200 组数据. 图3 镍基合金有限元模型示意图(单位:mm)Fig.3 Finite element model of Ni-based alloy (unit:mm) 本文建立了3 种机器学习模型,分别是支持向量回归模型(support vector regression,SVR)、长短期记忆神经网络(long short-term memory,LSTM)和前馈神经网络(feed forward neural network,FFNN).在SVR 模型和FFNN 模型中,将选定的6 个非局部晶体塑性模型参数作为输入参数,屈服应力和最终应力作为输出参数.而在LSTM模型中,输入参数为6 个非局部晶体塑性模型参数和应变,每个参数序列长度均设置为200,输出结果为应力.在SVR 模型中采用多项式核函数,其多项式次数为3.在神经网络中,使用均方误差(mean squared error,MSE)作为损失函数,其可以表示为 其中,n为样本数量,yi为样本标签,为机器学习的预测值.同时使用决定系数R2来描述机器学习的回归效果,其表示为 图4 最终应力的(a)训练集和(b)测试集的数据分布;屈服应力的(c)训练集和(d)测试集的数据分布Fig.4 The data distribution of final stress in (a) the train dataset and(b) the test dataset;The data distribution of yield stress in (c) the train dataset and (d) the test dataset 基于以上数据,按照上述模型设置分别对3 个机器学习模型进行训练.并依据MSE对模型的训练结果进行评估,经过机器学习模型参数调整后,完成模型的训练,其模型最终性能可以通过MSE和决定系数R2表示,如表3 所示.与其他模型相比,LSTM的MSE最小,表明其模型性能最好.这表示了LSTM能够较好地预测应力-应变响应过程,且具有良好的泛化能力.这是因为LSTM 能够有效地学习数据的时序特征,该特点与输入数据更为契合.因此,在3 种模型的复杂程度相差不大的情况下,其MSE最小.而LSTM 对应的R2也最小,但是考虑到R2更适合用于评价线性回归结果,而LSTM 计算的标签是非线性的应力-应变曲线,因此R2难以反映出LSTM 的性能.SVR 和FFNN 使用的标签符合线性回归,其R2也反映了二者能够对屈服应力和最终应力进行准确的预测. 表3 不同机器学习模型的性能表现Table 3 Performance of different machine learning model 基于训练完成的机器学习模型,通过前文叙述的遗传算法模型进行本构模型参数确定.将遗传算法的迭代次数设置为500,种群大小为1000,交叉率和变异率分别为65%和10%.以评价公式的结果作为误差,用以求解非局部晶体塑性模型参数.在算法运算过程中,每代种群中最优个体的误差变化过程如图5 所示,最终的误差值见表4.评价值越小,表明其结果与实验结果越接近.从图中可得,使用了不同机器学习模型的遗传算法模型均可收敛,并且最终的误差均较小.遗传算法模型在迭代100 次左右时已接近收敛,而使用FFNN 的遗传算法模型收敛速度最快,且其最终精度最高. 表4 遗传算法的最终误差Table 4 The final error of genetic algorithm 图5 遗传算法中每代误差变化Fig.5 The variation of the error in every generation of genetic algorithm 遗传算法得到的晶体塑性模型参数见表5.不同机器学习模型的遗传算法优化结果有一定差异,主要有两个原因:一是不同模型的精度影响了收敛区域的大小;二是同一条应力-应变曲线可能对应多组晶体塑性模型参数,导致了多解现象,且每个解的收敛区域也不相同.其次,部分参数在使用不同机器学习模型的情况下取值范围比较接近,例如参数k2在设定最大值为60 的情况下,各个模型下取值都超过50;参数p和参数q的取值都接近1.为了验证这3 个参数的分布情况,本文采用FFNN 作为机器学习模型,用遗传算法进行了50 次求解,其参数取值分布如图6 所示.这3 个参数的数值分布比较集中,其中参数p和参数q的平均值都接近1.参数分布的稳定性说明它们对屈服应力和最终应力有较大的影响,因此模型求解得到的参数接近. 表5 根据不同机器学习模型得到的晶体塑性模型参数Table 5 Crystal plasticity parameter obtained by different machine learning model 图6 遗传算法得到的参数最优解分布图Fig.6 The distribution of the optimal parameters obtained by the genetic algorithm model 将遗传算法模型得到的参数代入已建立的有限元模型中进行计算,并将计算结果与实验结果进行对比.如图7 所示,3 种模型得到的应力-应变曲线整体上均与实验曲线接近,并且二者的曲线趋势一致,只有硬化阶段存在较小差异.由于评价公式主要关注屈服点和应变最大处的应力,而由遗传算法计算得到的最终误差值均不超过0.02,如表4 所示,因此在这两点处模拟结果与实验曲线重合程度高.该模型得到的参数能够满足要求,参数对应的应力-应变曲线符合实验趋势. 图7 基于优化程序得到参数的晶体塑性有限元模拟结果与实验结果的对比Fig.7 The crystal plasticity results of finite element simulation with the parameters obtained by the optimization program are compared with the experimental results 注意到模拟结果与实验结果在塑性阶段存在一定偏差.考虑到大多数金属的应变硬化行为,可以用指数曲线来描述:.其中 σT和 εT分别表示真应力和真应变,K表示强度系数,n表示应变硬化指数.硬化指数n可以描述金属的应变硬化程度,因此可以将其作为评价指标之一,引入到式(14) 中.LSTM 可以输出应力-曲线从而计算曲线的硬化指数,故选择使用LSTM 作为机器学习模型.在遗传算法中引入硬化指数n作为评价指标,并使用LSTM作为机器学习模型,此新模型记作LSTM-1. 将优化求解得到的参数代入有限元模型中进行计算,结果如图8 所示.本文使用了应力-应变曲线下面积差值的绝对值作为指标来评价曲线与实验数据的拟合情况,各个模型结果在表6 中列出.机器学习模型的性能越好,其应力-应变曲线拟合越好,LSTM,FFNN 和SVR 3 个模型得到的曲线均能够很好地与实验数据吻合.在引入硬化指数作为评价指标后,拟合效果得到了明显的提升.这表明,本文引入的硬化指数能够有效地反映出实验数据的特征,从而提高了优化模型的准确性. 表6 不同模型得到的应力-应变曲线与实验数据的拟合情况Table 6 Fitting results of stress-strain curves obtained by different models and experimental data 图8 引入硬化指数n 后,有限元模拟结果与实验结果的对比Fig.8 Comparison of the finite element simulation results and experimental results after introducing the hardening index n 本文借助SHAP 工具,基于Shapley 值的原理对机器学习模型进行解释.通过机器学习模型计算得到了晶体塑性模型参数在屈服应力和最终应力下的Shapley 值,并根据大小进行了排序,如图9 所示.Shapley 值的大小表示了参数对结果的边际效应影响,发现p和q对屈服应力和最终应力均有较大的影响.值得注意的是,k2对屈服应力影响较小,而对最终应力影响较大. 图9 对结果影响最大的特征Fig.9 The most important features affect 为了更加明确地表示各个特征取值变化对结果的影响和作用,我们通过SHAP 工具,基于数据集的数据分布,绘制了特征取值对屈服应力和最终应力的影响,如图10 所示.图中一个点代表一个样本,颜色越红说明特征本身数值越大,颜色越蓝说明特征本身数值越小.这里根据数据集来说明参数数值变化时对屈服应力和最终应力造成的影响.在屈服应力图中,p越大,q和f越小,屈服应力越大;而在最终应力图中,p越大,q和k2越小,最终应力越大. 图10 特征的取值产生的影响Fig.10 Effects of features’ values 我们将相应的参数在范围内变化,并带入有限元模型中进行验证,结果如图11 所示.由图可知,当p值增大时,屈服应力和最终应力均增加;当q增大时,二者均减小;当k2增大时,屈服应力仅发生微小的变化,最终应力出现下降的趋势.有限元计算结果与预测结果一致,证明了Shapley 值能够有效地说明特征变化产生的影响. 图11 基于有限元模拟,参数(a) p,(b) q,(c) k2 增大时最终应力和屈服应力的变化Fig.11 Based on finite element simulation,the changes of final stress and yield stress when parameters (a) p,(b) q,and (c) k2 increase 关于该现象可以从非局部晶体塑性本构模型中得到解释.p和q主要是通过式(6)影响位错速度vα,进而影响 α 滑移系上的塑性滑移率,因此当p增大或q减小时,对应的 α 滑移系上的塑性滑移率减小,最终应力值也会增大.由于选取的屈服点是根据应力-应变曲线进行选取的,在该点状态下实际上已经出现了部分滑移系的开动,因此p和q对屈服应力的影响趋势与最终应力一致.参数k2用于调控位错运动的平均自由程的大小,所以当k2变大时,位错运动的平均自由程变大,意味着位错运动遇到的障碍强度变弱,因此最终应力会减小.因此,根据SHAP 分析得到参数变化产生的影响结果与理论一致,这表明其能够有效地展示参数变化导致的影响. 本文将镍基高温合金材料的晶体塑性有限元数据用于训练机器学习模型,并在遗传算法中耦合了机器学习模型,确定了镍基高温合金的晶体塑性模型参数,得到主要结论如下. (1) 本文建立耦合机器学习的遗传算法本构模型参数求解模型,该方法可以根据应力-应变曲线确定对应的非局部晶体塑性模型参数,并在精度上满足要求. (2) 通过计算Shapley 值,可以得到各个参数对屈服应力和最终应力的边际影响相对大小.根据Shapley 值的变化,可以从数据分布中得出特征变化对结果产生的影响:p增大或q减小时,屈服应力和最终应力均增加;而k2增大时,屈服应力仅出现微小变化,最终应力出现下降趋势. (3) 基于SHAP 框架得到本构参数变化影响的分析结果可以通过晶体塑性本构理论和有限元模拟进行验证,并且其变化趋势与有限元模拟和理论分析一致.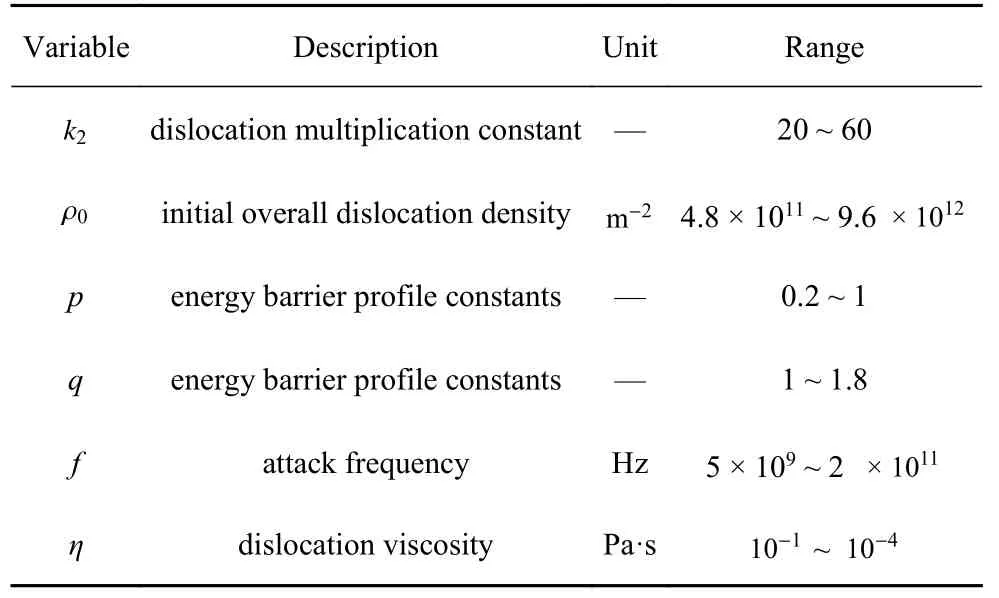
2.2 数据生成

3 结果与讨论
3.1 遗传算法计算结果






3.2 基于SHAP 的机器学习模型分析
4 结论
