Finite-time Prescribed Performance Time-Varying Formation Control for Second-Order Multi-Agent Systems With Non-Strict Feedback Based on a Neural Network Observer

Chi Ma ,,, and Dianbiao Dong ,,

Abstract—This paper studies the problem of time-varying formation control with finite-time prescribed performance for nonstrict feedback second-order multi-agent systems with unmeasured states and unknown nonlinearities.To eliminate nonlinearities, neural networks are applied to approximate the inherent dynamics of the system.In addition, due to the limitations of the actual working conditions, each follower agent can only obtain the locally measurable partial state information of the leader agent.To address this problem, a neural network state observer based on the leader state information is designed.Then, a finite-time prescribed performance adaptive output feedback control strategy is proposed by restricting the sliding mode surface to a prescribed region, which ensures that the closed-loop system has practical finite-time stability and that formation errors of the multi-agent systems converge to the prescribed performance bound in finite time.Finally, a numerical simulation is provided to demonstrate the practicality and effectiveness of the developed algorithm.

I.INTRODUCTION

DUE to the characteristics of interactivity, coordination,targeting, adaptability, and intelligence, multi-agent systems (MASs) such as (unmanned aerial vehicles (UAVs) [1],formation satellites [2], robots [3], etc., are widely studied and have become a research hotspot for intelligent control.In recent years, a challenging issue in the realm of MASs control has been time-varying formation control with unknown nonlinearities.With the rise of sliding mode control (SMC),applications of fuzzy logic systems (FLSs), and neural networks (NNs) with nonlinear function approximation capabilities for time-varying formation control of unknown nonlinear MASs, MASs control theory has achieved excellent research results, see [4]–[11].The authors in [7] studied the time-varying formation problem, consensus tracking problem, and target encirclement problem for linear MASs with multi-leaders and followers, categorizing them as partially informative good or unknown.Reference [8] proposes an optimally adaptive formation control scheme for unknown robots by using NN based recognizers to approximate formation dynamics.References [9] and [10] proposed adaptive formation control for MASs by approximating unknown nonlinear functions through NNs and FLSs, respectively.Reference [11] demonstrated a discontinuous SMC tracking algorithm that provides a control framework for adaptive coherent tracking of secondorder nonlinear MASs in disturbance and actuator fault environments.

It is worth noting that the premise of the above research is that the state information of the controlled system is known.However, in practical applications, limitations in system sensors and cost control lead to feedback of only part of the state or only the output.The study of system output feedback control has significant theoretical scientific value in this setting,as well as providing useful practical advice, see [12]–[20].The authors of [13] and [14] designed a distributed observerbased distributed control technique for linear MASs.Based on observers, [15] and [16] built distributed adaptive controllers for linear MASs and heterogeneous MASs, respectively.References [17] and [18] used observers to estimate external disturbances and unknown states of nonlinear systems, respectively, and realize tracking control of nonlinear MASs.By using neural network (NN) state observers, [19] presented a time-varying optimal control for unknown nonlinear MASs.Reference [20] proposed a nonfragile tracking control protocol considering communication delays for the robust tracking problem of linear MASs by an intermediate estimator withstanding random faults.

The issue of finite time controllability cannot be resolved by any of the aforementioned studies.The convergence speed,however, is a crucial sign of the effectiveness of the system control in real-world settings.By building a sliding mode protocol, [21] presented the finite-time consensus control of MASs in a perturbed environment.For distributed secondorder MASs, [22] examined finite-time tracking control and formation control using observer-based control techniques.Based on the general sliding model, [23] designed a fast distributed finite-time consensus control framework for MASs under disturbance environment.

Prescribed performance control (PPC) has undergone extensive research since it was first proposed in [24], ensuring the steady-state and transient performance of the system.By imposing performance constraints, [25] and [26] investigated the issue of decentralized formation control.Combined with directed topology, [27] and [28] achieved time-varying formation control of MASs with prescribed performance.

Furthermore, some scholars have also made some achievements in finite time prescribed performance control (FTPPC).For the tracking problem of nonlinear systems with non-strict feedback, [29] studied FTPPC.Using NN approximation uncertainty and a finite-time performance function (FTPF),[30] investigated the FTPPC issue for unmodeled stochastic nonlinear systems.Reference [31] implemented adaptive fuzzy control of FTPF for a strict feedback system that generates actuator faults in disturbance environments.On this foundation, another group of scholars introduced output feedback.By applying FLSs observers, [32]–[34] examined finite-time adaptive fuzzy PPC for nonlinear systems.Reference [35]proposed an FTPPC strategy with output feedback to study finite-time adaptive fuzzy PPC for quadrotor UAVs by using a NN observer for output feedback.

From the above perspective, it can be found that there is a paucity of studies considering both FTPPC and output feedback.However, to our best knowledge, there are no studies of FTPPC for the time-varying formation of MASs with output feedback.Therefore, a finite-time prescribed performance time-varying formation control technique based on NN observers for a class of non-strict feedback second-order MASs with unmeasured states and nonlinear uncertainties, is proposed in this study.The primary innovations are as follows:

1) For the time-varying formation problem of non-strict feedback MASs, a finite-time prescribed performance timevarying formation control algorithm is proposed in this paper.By restricting the estimated sliding mode surface to a prescribed performance region, a new swarm controller is designed.

2) Compared with the existing FTPPC methods for MASs[36]–[38], this paper considers the information unmeasured state or partial feedback information of the system and designs the NN state observers for MASs, which not only ensures the transient and steady-state characteristics during time-varying formation control of MASs, but also addresses the unknowability and unmeasurability of the system.

3) Although [32]–[34], [39], [40] have conducted studies of FTPPC with output feedback, these studies are focused on single nonlinear systems.In contrast, this paper extends the research object from the single nonlinear system to the MASs by establishing communication topology relations.

II.PRELIMINARIES

A. Graph Theory

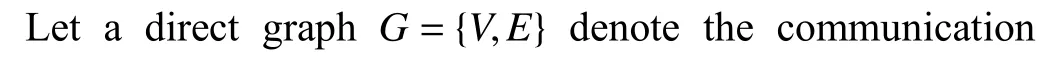
B. Finite-Time Stability Theory

Firstly, the finite-time stability theory and associated fundamental lemmas are presented.

Definition 1[29],[41]: Consider the following system:

where the state vector is determined byxandf(t,x) represents a continuous nonlinear function.System (1) is semiglobal practical finite-time (SGPF) stable when there is a stable timeT(x0) such that //x(t)//≤∆,t≥T, and Δ is a normal number.

Lemma 1[42]: If there are positive constants ν1and ν2,ν1>0 and 0<ν2<1 for a positive smooth definite functionV(x), then there are the following:

Then, the system converges in finite convergence time.The initial statex0determines the finite-time, which can be given by

Lemma 2[43]: For τ1≥0, τ2≥0, τ3≥0 , τ¯ ≥0 , τ≥0 and π ≥0, there is the following:

Lemma 3: The Young’s inequality is defined as

wherex,y∈R,p>1,q>1,ϑis a positive number, and(p-1)(q-1)=1.

C. Prescribed Performance Control

Definition 2: When the performance function ρe(t) is: 1)positive, 2) smooth, 3) strictly decreasing, it is the prescribed performance function.The performance function introduces prescribed bounds.

According to Definition 2, the FTPF (proposed in [29]) can be given as

where ρe0is a constant, ρeT f=limt→T fρe(t) is the steady-state error bound,Tfdenotes the setting time.

D. Neural Networks

Nonlinear functions can be efficiently approximated by NNs.Consider an unknown functionf(x): Rℓ→R, there is the following:

III.PROBLEM STATEMENT AND CONTROL STRATEGY

A. Problem Descriptions

There is a class of MASs with non-strict feedback withNagents, which has unknown nonlinearities and unmeasured states.Thei-th follower’s states are characterized by

Remark 3: In swarm control, the distance between individuals is always time-varying due to different formation configurations, such as various attitudes and tracking ranges.The control formation maintains control under the condition thatℓiis a non-zero constant vector.Once ℓi=0, (10) changes into tracking control with leader-follower consensus.As a result,time-varying formation control has specific cases known as formation maintainance control and consensus control.

Therefore, the formation tracking error is given by

whereei,0andei,1are formation tracking errors.

Control Objective:Applying the finite-time prescribed performance time-varying formation strategy to a class of nonstrict feedback second-order MASs with unmeasured states and unknown nonlinearities (5) and (6), i) It is possible to obtain (10) with unknown dynamics and locally unmeasured states by using an adaptive NN state observer; ii) A time-varying formation control with prescribed performance can be achieved in a finite amount of time by using SMC and FTPF.

B. State Observer Design of Neural Networks

NN state observers are designed to estimate unmeasured states of systems with unknown dynamics, as follows:

wheregˆi,j(·) is the estimate ofgi,j(·) in (7) and are approximated by NN

In addition, the NN approximation errors are given by

C. Control Strategy

The NN state observers in (12) and the adaptive law (18)will play a significant role in FTPPC for the MASs in (5) and(6).Firstly, we define the time-varying estimation errors as

The dynamics of the time-varying estimation errors are deduced from (24)

Then, the time-varying MASs formation control estimation error is denoted as

Then, (26) is given by

Let

We can infer that

where

The designed sliding mode function isS=λε0+ε1, taking

where

Taking the derivative of (30), we have

Then, it can be inferred that

wherel2>0.Basedontheabovetheory, the sliding mode errorSˆandεˆτareSGPFwhen satisfied

Remark 6: Compared with the existing FTC results (see Lemma 1), the Lyapunov function used in this paper is more direct and less restrictive, avoiding the ambiguity problem.

IV.DIGITAL ANALOG SIMULATION

In this section, we design a systematic case to evaluate the proposed method.The errors of all signals in non-strict feedback second-order MASs with unmeasured states and unknown nonlinearities converge within the prescribed performance range in a finite amount of time when the designed controller is applied to the designed system case, effectively realizing the time-varying formation control.

Assuming the MASs have six agents, the states of the following agent are provided by:

The communication matrix is

The FTPF is given by

The critical simulation results are depicted in Figs.1-13,which prove the effectiveness of the presented control strategy.Figs.1 and 2 show the position and velocity states of MASs in time-varying formation control, respectively, where the intrinsic nonlinear functions of the second-order MASs are unknown.The behavior of the followers is affected by the leader reference signalg0,0.There is no information synergy between the position and velocity data of agents because of the time-varying formation functions.The performance of the NN state observers based time-varying formation control for leader-followers is shown in Figs.3 and 4, and it is evident that the location and velocity errors of the second-order MASs are contained within a prescribed area and stable until the setting timeTf.The effects of the NN state observer under timevarying formations and the approximate effects on the unmeasurable velocity states are depicted in Figs.5 and 6, respectively.Fig.6 shows that the velocity states can be observed well, demonstrating the efficiency of the observer setup.Fig.7 shows the sliding mode errors of the 4th agent at different settling timesTf.It is obvious that the sliding mode errors work as expected regardless of the setting timeTf.Fig.8 shows the comparison of sliding mode error of the 4th agent with FTPPC and PPC time-varying formation control.The PPC uses the exponential performance function from the literature [28]ve(t)=(νe0-νe∞)e-lt+νe∞where νe0=4.9, νe∞=0.1,l=0.4.It is clear from the figure that finite time convergence of the sliding mode error cannot be achieved when using the exponential performance function approach in [28].And when FTPPC is used, the convergence time of the sliding mode error of the 4th agent can be accelerated.Fig.9 shows the comparison results of the time-varying formation tracking error of the 4th agent of FTC and FTPPC.It is obvious that the proposed strategy can accelerate convergence time compared to [4] using the terminal sliding mode to realize FTC.Fig.10 shows that the weight parametrizations of NNs are bounded.Fig.11 gives the control input information of the second-order MASs.From these plots, we can find that the time-varying formation performance of the MASs is acceptable when the proposed method is applied, despite the presence of unknown nonlinear functions and unmeasured state information.

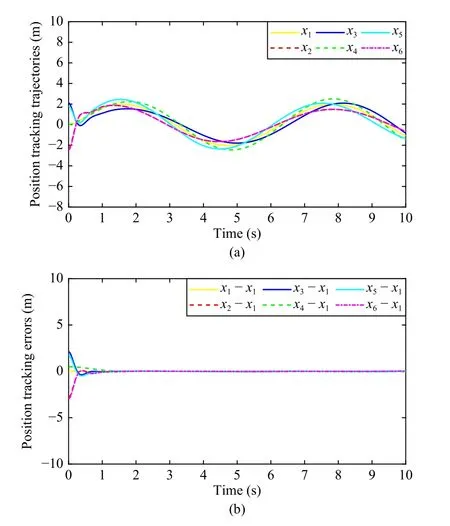
Fig.1.The position states of MASs under time-varying control.(a) Position behaviors; (b) Position tracking errors.Let xi represent position behavior under time-varying formation of the i-th agent.The position tracking errors under time-varying formation control among MASs are within the error tolerance.

Fig.2.The velocity states of MASs under time-varying formation control.(a) Velocity behaviors; (b) Velocity tracking errors.Let vi represent velocity behavior under time-varying formation control of the i-th agent.The timevarying formation of velocity errors among MASs are within the error tolerance.

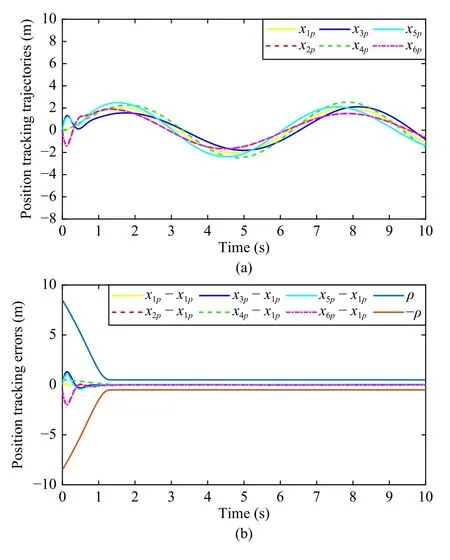
Fig.3.The NN observers based position states of MASs under time-varying formation control.(a) The NN state observers based position tracking trajectories; (b) The NN state observers based position tracking errors.Let xip and ρ represent the NN observer based position behavior under time-varying formation of the i-th agent and the FTPF, respectively.The position tracking errors are restricted to a prescribed region and have stabilized until settling time T f =2 s.

Fig.5.The position behavior of MASs.(a)–(f) represent the comparison of the 1st to 6th agents in the position behavior and the NN observer based position behavior, respectively.

Fig.6.The velocity behavior of MASs.(a)-(f) represent the comparison of the 1st to 6th agents in the velocity behavior and the NN observer based velocity behavior, respectively.This result shows that unmeasured velocity information can be well obtained by NN observers.

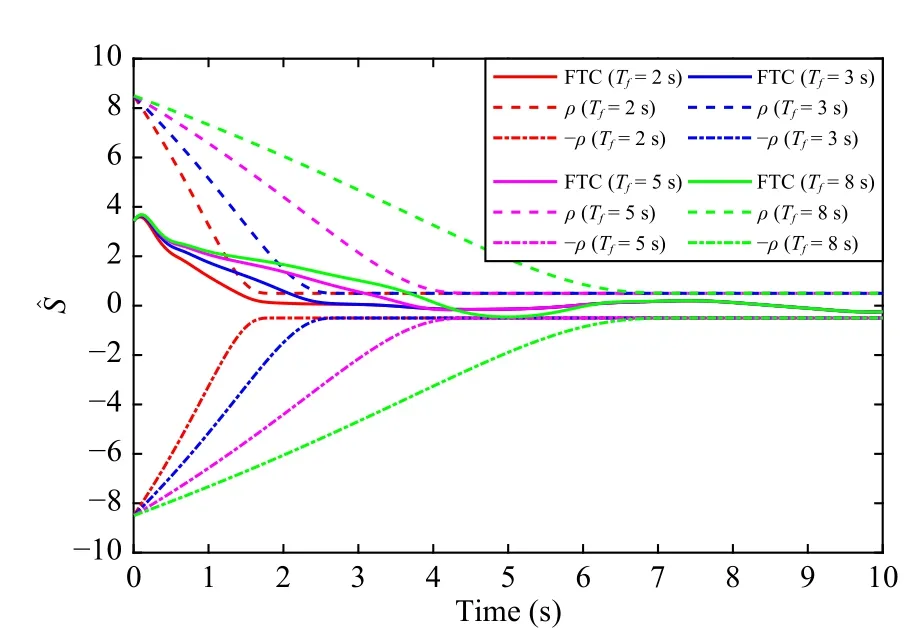
Fig.7.Sliding mode errors of the 4th agent with time-varying formation control on the various settling times Tf.When the set time Tf changes, the sliding model error S of the 4th agent is always limited to a prescribed region.

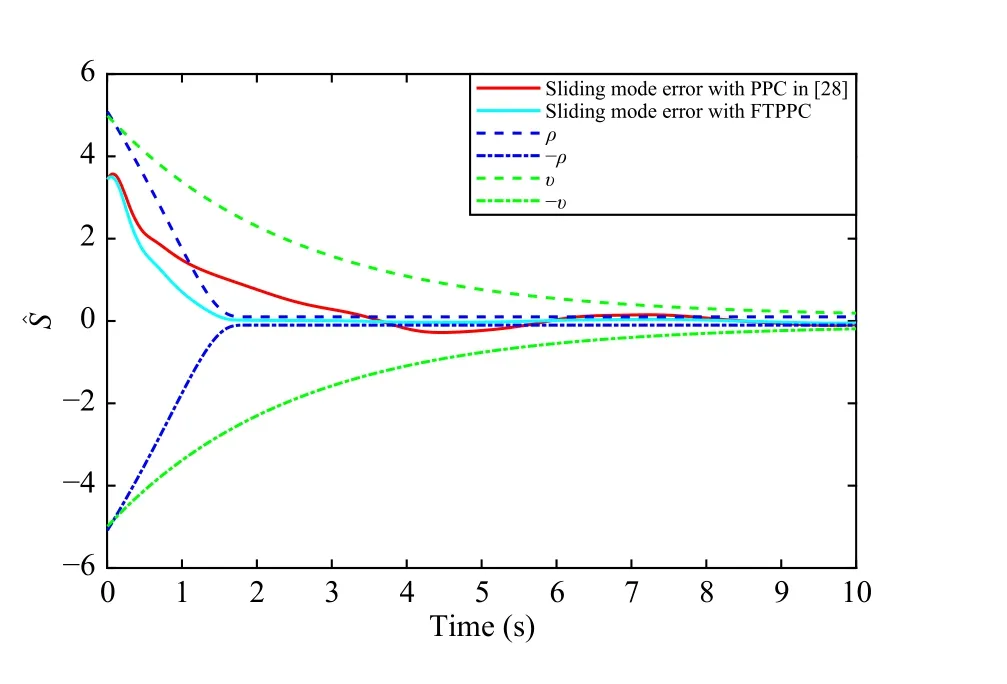
Fig.8.Comparison of the sliding mode error of the 4th agent of PPC and FTPPC.Compared with the sliding mode error of the 4th agent in [28], the convergence time of the sliding mode error of the 4th agent can be accelerated when FTPPC is used.

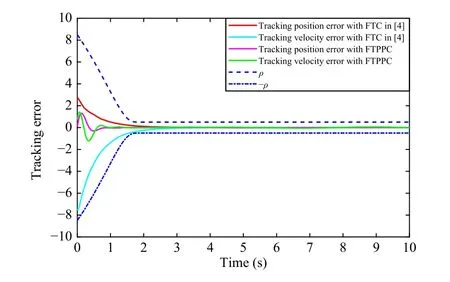
Fig.9.The comparison results of the time-varying formation tracking error of the 4th agent of FTC and FTPPC.The tracking errors of the 4th agent of FTPPC time-varying formation control are limited to a prescribed region.Compared with [4] using the terminal sliding mode to realize FTC, the proposed strategy can accelerate the convergence time.

The position and velocity consensus errors (ℓi=0) for MASs with and without the FTPF restriction are depicted in Figs.12 and 13, respectively.The corresponding controllers are designed as

Fig.10.Norm trajectories of NN weights //ω//.(a) Weight norm ;(b) Weight norm ■■

Fig.11.Control inputs for MASs.

whereαis the adjustment gain, after which we let α=1.6.As depicted in Figs.12 and 13, the position and velocity error of the 3rd agent can reach convergence faster with the FTPF compared to without the FTPF.Different convergence speeds can be obtained by changing the setting timeTf.

V.CONCLUSION

This paper addresses the finite-time prescribed performance time-varying formation control problem for non-strict feedback second-order MASs with unmeasured states and unknown nonlinearities.The unknown nonlinear dynamics of the system are learned by NN, based on which NN state observers are designed to solve the unmeasured state information of the system.In addition, an adaptive NN output feedback control scheme is developed by restricting the sliding mode surface to a prescribed region.With rigorous theoretical analysis, the finite-time stability of the closed-loop system is illustrated, and formation errors of the MASs converge to the prescribed performance bound in finite time.Finally, simulation results demonstrate the practicality and effectiveness of the developed control algorithm.

Fig.12.Position tracking errors of the 3rd agent on different settling times Tfwith consensus control.The position consensus error of the 3rd agent is restricted to a prescribed region when the setting time Tf varies.When FTPF is introduced, the convergence time of the 3rd agent position consensus error can be accelerated to be faster than without FTPF.

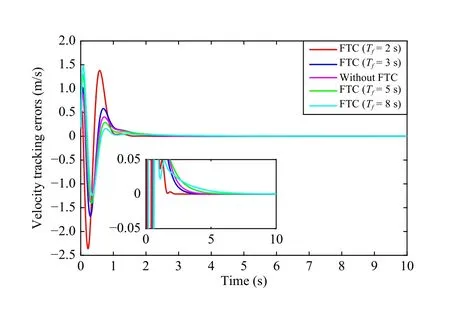
Fig.13.Velocity tracking errors of the 3rd agent on different settling times Tfwith consensus control.The velocity consensus error of the 3rd agent is restricted to a prescribed region when the setting time Tf varies.When FTPF is introduced, the convergence time of the 3rd agent velocity consensus error can be accelerated to be faster than without FTPF.