Computational Experiments for Complex Social Systems: Experiment Design and Generative Explanation

Xiao Xue ,,, Deyu Zhou , Graduate Student,, Xiangning Yu ,Graduate Student,, Gang Wang , Juanjuan Li ,,,Xia Xie , Lizhen Cui ,,, and Fei-Yue Wang ,,

Abstract—Powered by advanced information technology, more and more complex systems are exhibiting characteristics of the cyber-physical-social systems (CPSS).In this context, computational experiments method has emerged as a novel approach for the design, analysis, management, control, and integration of CPSS, which can realize the causal analysis of complex systems by means of “algorithmization” of “counterfactuals”.However,because CPSS involve human and social factors (e.g., autonomy,initiative, and sociality), it is difficult for traditional design of experiment (DOE) methods to achieve the generative explanation of system emergence.To address this challenge, this paper proposes an integrated approach to the design of computational experiments, incorporating three key modules: 1) Descriptive module: Determining the influencing factors and response variables of the system by means of the modeling of an artificial society; 2) Interpretative module: Selecting factorial experimental design solution to identify the relationship between influencing factors and macro phenomena; 3) Predictive module: Building a meta-model that is equivalent to artificial society to explore its operating laws.Finally, a case study of crowd-sourcing platforms is presented to illustrate the application process and effectiveness of the proposed approach, which can reveal the social impact of algorithmic behavior on “rider race”.

I.INTRODUCTION

POWERED by the rapid development of Internet, the penetration of the Internet of Things, the emergence of big data, and the rise of social media, more and more complex systems are exhibiting the characteristics of social, physical,and information fusion, commonly referred to as cyber-physical-social systems (CPSS) [1], [2].As a result, the social, economic, political, and cultural activities of billions of people have effectively been digitized, and the big data analysis has become a mainstream technology in computational social science.But, it encounters significant challenges: 1) In many instances, big data serves as a form of sampling and is often noisier and less “designed” in comparison to traditional social surveys and laboratory experiments.2) The behavioral patterns derived from big data, whether from individuals or groups, may not necessarily align with real-life behaviors.3) Big data can be distorted due to various factors, such as news viewing data being influenced by recommendation algorithms.

The integration of experiments into research allows scholars to move beyond correlations in naturally occurring data,which provides a more reliable means to address cause-andeffect questions.Currently, numerous social experiments are conducted through online platforms, resulting in so-called virtual laboratories.The crowd-sourcing platforms like Amazon’s Mechanical Turk can be considered as virtual experiments.However, the challenges faced by the virtual laboratories research are largely similar to those encountered in big data analytics, as both involve analyzing data related to human behavior.The intricate nature of human behavior and experience, characterized by their high diversity, subjectivity, and unpredictability, presents a significant hurdle.This complexity leads to a lack of the systematic experiment design methods that are capable of generating robust data for causal inference, particularly in understanding the emergence and dynamics of complex social systems.In this context, computational experiments provide a new way to explain, illustrate, guide and reshape complex phenomena in the real world, which can realize the quantitative analysis of complex systems by means of “algorithmization” of “counterfactuals” [3].In the realm of computational experiments, the capability to set up multiple controlled experiments concurrently is a key advantage.This allows for intentional alterations in the parameters of artificial societies or the application of specific intervention measures.By comparing the outcomes of these experiments and, where necessary, conducting large-scale repetitive simulations,researchers can effectively unearth the underlying causes of complex phenomena.

The basic setting of computational experiments is to recognize the inherent uncertainty in both the future outcomes of a system and the pathways of achieving those outcomes.As shown in Fig.1, computational experiments method offers a distinctive path for “generative explanation”.This approach relies on data and domain knowledge to simulate and analyze real-world scenarios.Data plays a pivotal role in three main areas: initializing the model, verifying the model, and extracting agent rules.In this setup, agents act as containers for applying knowledge.The knowledge library is comprehensive, encompassing various elements such as the structural prototype of an agent, behavioral rules, learning rules, environmental update rules, and other relevant domain knowledge.In the output module, the results from these experiments can be displayed in a variety of visual media formats, including two-dimensional scene, three-dimensional scene, image, text and others.Utilizing the data obtained from these experiments, the decision analysis model can evaluate the influence of various parameters on the evolution of the system.The process of “generative explanation” through computational experiments method is characterized by two key aspects: generative deduction and generative experiments [4].As shown in the middle of Fig.1, the details of the two aspects are presented as follows:

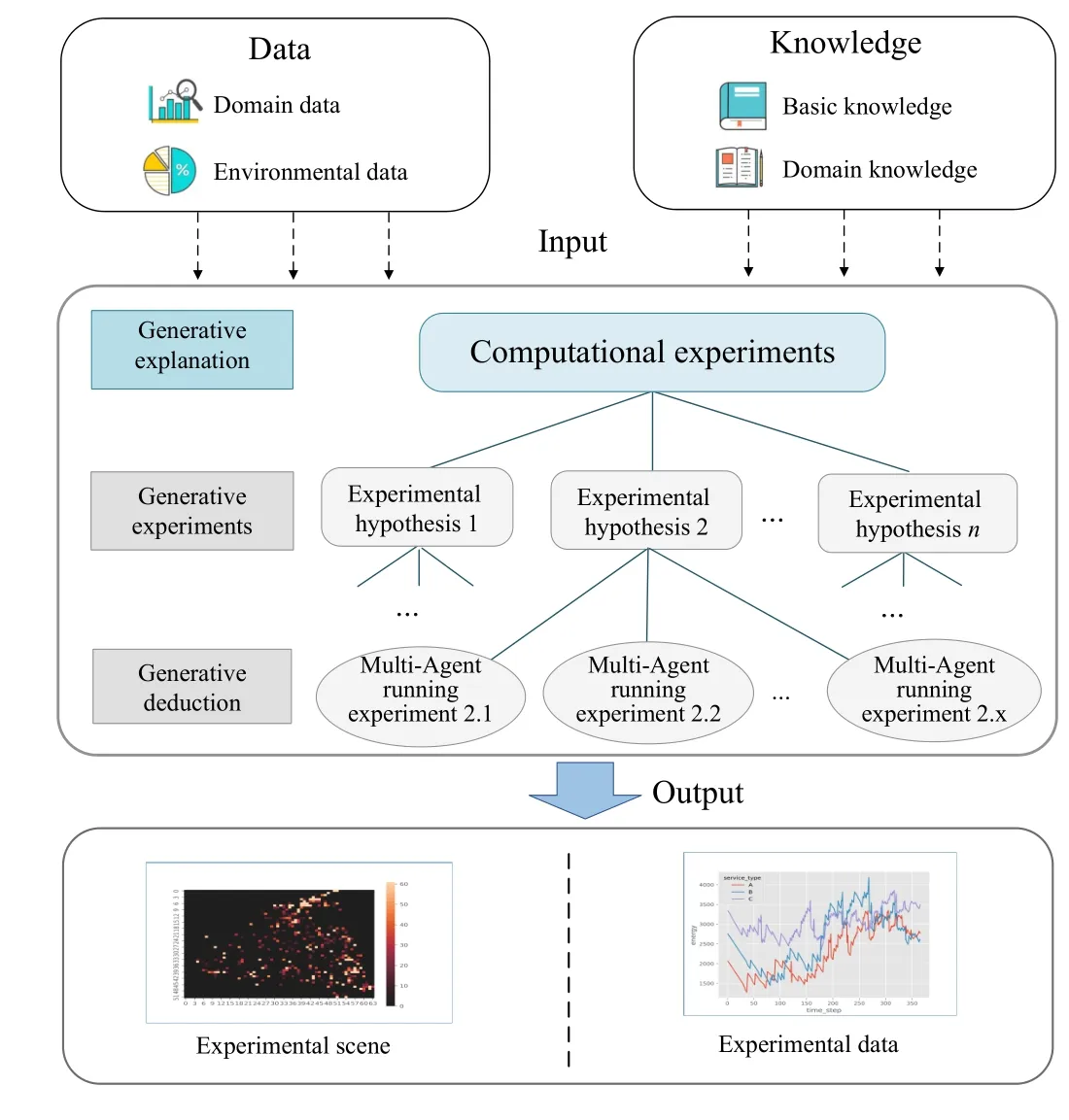
Fig.1.The principle diagram of computational experiments.

1)Generative Experiments: are used to validate certain theories or hypotheses by introducing artificial interventions into artificial societies, generating data that is highly suitable for investigating causal relationships [5].By modifying the rules,parameters, and external intervention of experiment system,various combinations of these experimental elements can be carried out repeatedly within a cultivated “artificial laboratory”.

2)Generative Deduction: employs deductive simulation to replicate real-world settings or phenomena, or construct and observe potential alternative worlds.With the continuous interaction of a vast number of agents, the entire artificial society generates new content and influences the future decisions of agents, thus achieving a dynamic equilibrium and self-sustaining ecosystem, ultimately resulting in the emergence of various story-lines [6].It allows for the observation and identification of the causal factors (independent variables)responsible for the observed changes in the output response(dependent variables).

As the complexity of the system increases, the number of combinations of impact factors grows exponentially.This leads to the successful application of computational experiments mainly depending on the design of experiment, which involves determining the experimental subjects, objectives,and intervention methods.For instance, the experiment may focus on variance or treatment effects, the experimental population may be homogeneous or heterogeneous, and the factors under investigation may be single or multiple.Furthermore,these human and social factors encompass elements of randomness and initiative, contributing to the resulting complexity (Table I).These straightforward application of traditional design of experiment (DOE) methods may prove insufficient in addressing the unique and complex challenges inherent in computational experiments.Consequently, how to design computational experiments reasonably to achieve the target is the research issue in the filed.

Against the background, this paper proposes an integrated method for the design computational experiments: i) Based on descriptive modeling of artificial society, the influencing factors and response variables of the system are determined; ii)Based on interpretative characteristics of experimental design,the factorial experimental methods of determinism and randomness are described; iii) Based on the data relating to the artificial society inputs and outputs, a meta-model is developed to provide predictive insights into the system dynamics.

The remaining parts of this paper are organized as follows.Section II introduces the research background and our research motivation.Section III presents the design framework of computational experiments, comprising three primary components: descriptive modeling of artificial society,interpretative modeling of experiment design, and predictive modeling of meta models.Sections IV-VI discuss the details of the three steps respectively.Section VII presents a case study to validate the effectiveness of the experiment design framework.Section VIII concludes the paper.

II.BACKGROUND AND MOTIVATION

In 2009, David Lazer and a group of distinguished scholars published a seminal article inSciencetitled “Computational Social Science” [7].This publication marked the birth of an interdisciplinary research field known as “computational social sciences”, which has gained significant attention from scholars across multiple disciplines, such as social science and computer science.As our capacity to collect and analyze extensive datasets continues to advance, the field of computational sociology is rapidly growing, driven by data-driven approaches.

Traditionally, social scientists prioritize providing satisfactory explanations for the behavior of social systems, often relying on causal mechanisms from entity theories.In contrast, computer scientists traditionally focus more on developing accurate predictive models, regardless of whether they conform to causal mechanisms or even if they can provide explanations.Table II presents four quadrants to depict varying degrees of emphasis on explanation and prediction,including descriptive modeling, explanatory modeling, predictive modeling, and integrative modeling [8].

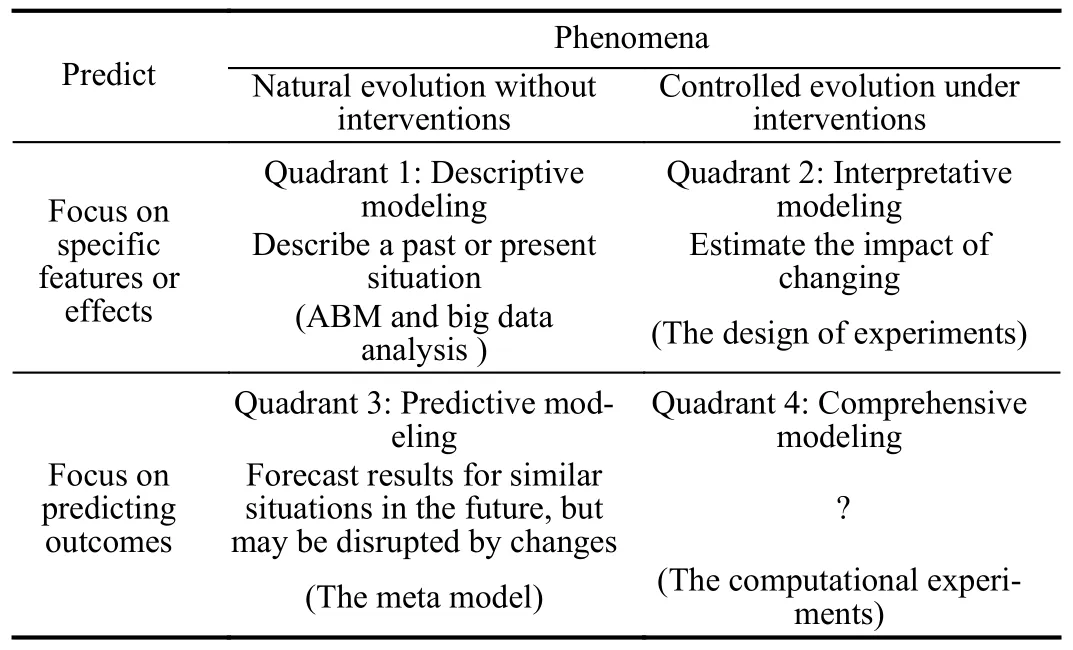
TABLE II RESEARCH METHOD CLASSIFICATION OF COMPUTATIONAL SOCIAL SCIENCES

Descriptive modeling (Quadrant 1) tends to prioritize simplicity, focusing on a limited number of properties that may influence the desired outcome.It argues that excessive emphasis on unnecessary details can compromise the model’s effectiveness in theoretical research.ABM treats social simulation as a virtual laboratory, enabling researchers to explore diverse social phenomena [9].ABM is highly valuable for understanding individual causal relationships, developing theoretical models, and even guiding policy-making.Through modeling, researchers can gain deep insights into the underlying mechanisms of social phenomena.However, the validity of such social modeling studies has faced widespread scrutiny.Once the model deviates reality as a reference, it can potentially produce any desired result, granting it excessive flexibility [10].This observation alone is insufficient to draw independent research conclusions or establish a basis; it requires further validation in combination with other research methods.

Interpretative modeling (Quadrant 2) considers the model as a simulation of reality and pursues the model as close to reality as possible.However, it is important to note that achieving a close resemblance to reality involves incorporating relevant parameters in the model that reflect potential real-world influences on the studied process, rather than aiming for an exact replication of the real world.This is because society is an open system, and even external factors unrelated to the process of interest can impact the phenomena being explained[7].The main challenge in such research is that as we strive for a close resemblance between the model and reality, the model becomes highly complex, making it difficult to discern the specific mechanisms responsible for the studied phenomena, thereby defeating the purpose of modeling.

Predictive modeling (Quadrant 3) involves combining ABM models with other techniques such as time series modeling,prediction contests, and supervised machine learning to comprehend and predict the behavior of complex social systems[11].This approach focuses on generating predictions that generalize well to future.By studying such models, we can gain new insights into social phenomena and provide support for decision-making.From a policy perspective, it is helpful to make high-quality predictions about future events, even if those predictions are not causal in nature.However, these methods often assume that the data used for training and testing the model originates from the same data generation process, as if making predictions in a static (albeit potentially noisy) world.Nonetheless, they may not perform well in settings where features or inputs are actively manipulated (e.g.,controlled experiments or policy changes) or when they fluctuate due to other uncontrolled factors.

While traditional and computational social science research has extensively covered quadrants 1, 2, and 3, quadrant 4 remains relatively unexplored.Developing models that effectively integrate the interactions among relevant factors to produce high-quality predictions about future outcomes is inherently more challenging than developing models focused solely on isolated explanations or predictive capabilities.Computational experiments method is an approach for modeling and analyzing complex social systems, presenting a potential technical avenue for integrating descriptive, interpretative, and predictive functions [12].In this paper, experiment design is used as the clue to construct the comprehensive modeling framework of complex social systems: the artificial society is used as descriptive modeling, the factor experiment design is used to realize interpretative modeling, and the meta model is adopted as the tool of predictive modeling.

Fig.2.The comprehensive modeling framework based on the design of computational experiments.

III.THE COMPREHENSIVE MODELING FRAMEWORK BASED ON COMPUTATIONAL EXPERIMENTS DESIGN

CPSS is generally composed of a diverse range and large number of intelligent agents, including various biological entities (such as humans, organizations, institutions, etc.), as well as machines (such as intelligent terminals, devices, and software agents).In the context of human-machine fusion, numerous intelligent agents collaborate and allocate tasks to achieve a common objective.As the number of intelligent agents participating in collaboration increases, so does the probability of random deviations, resulting in the emergence of system eruption.Without establishing the comprehensive modeling of CPSS, these emergent processes remain implicit, hindering its continuous governance and improvement.

Compared to traditional research paths, computational experiments method offers a unique avenue for integrating descriptive modeling, interpretative modeling, and predictive modeling by means of generative deduction and generative experiments [13].Its core idea is not to explain social phenomena through universal social laws or identify statistically related factors, but to explore the mechanisms that demonstrate how social phenomena are generated.As shown in Fig.2, the comprehensive modeling framework based on computational experiments design consists of three modules:1) The descriptive module (the top of Fig.2), which needs to identify the influencing factors and response variables of system dynamic operation.2) The interpretative module (two sides of Fig.2), through factorial experiment design, observes the behavior of artificial society in the presence of interventions (e.g., new strategy, parameter changes) [14].3) The predictive module (bottom of Fig.2) builds a meta-model that provides insightful understanding of artificial society evolution.The details are as follows:

A. Module 1: Descriptive Module-Determine the Influencing Factors and Response Variables

Computational experiments utilize computer simulation technology to address the generative explanation of complex social system: How do distributed local interactions of heterogeneous agents generate given (macro) rules from the bottom up ? Generative questions are “how” rather than “why”, and their answers lie in transforming the generative process into an artificial society based on agents.In this process, the key is whether the interesting macro-level results can be generated from artificial society.If they cannot be generated, they cannot be explained.The generative sufficiency is a necessary condition for explaining how macro-level results emerge.

Artificial society provides a holistic description of complex systems in reality, following the principle of “simple consistency” [15], [16].Artificial society is essentially a formal logic model that examines the relationship between a small number of variables by controlling for other variables.As more and more variables are considered, accurately depicting the operation of artificial society becomes challenging.On the one hand, the development of an event is often the result of multiple factors working together; On the other hand, due to the complexity and uncertainty of various factors, it becomes difficult to depict their relationships.To better navigate the following interpretive modeling and predictive modeling, it is essential to follow these steps: 1) Identify influencing factors:Which factors affect the state and behavior of the system? 2)Analyze the path and manner of impact: How do these factors affect the system? 3) Explore deeper factors: What influences these factors?

B. Module 2: Interpretative Module-Factorial Experiment Design

As shown in Fig.2, experimental processes can often be visualized as a transforms process: from a combination of multiple inputs into an output with one or more observable response variables.Wherein,x1,x2,...,xmare the input of artificial society system;y1,y2,...,ynare the output of artificial society system;u1,u2,...,upare controllable factors or decisions;v1,v2,...,vqare uncontrollable factors or events.The purposes of experiment design are: 1) To determine the factor collection that influences the system output through the computational experiment; 2) To determine the most effective controllable factoruithrough computational experiments to make the output result closer to ideal level; 3) To determine the collection of controllable factoruithrough computational experiments to minimize the impact of in-controllable factors or eventsvion the system.

The most basic method to reveal the rules between the inputs and outputs is manual model exploration guided by analysts or experts.While this exploration process is the most direct and does not require advanced technical expertise, it tends to be biased and may leave some unexplored parts of the“interesting” input space.So, a more systematic approach to discover the relationship between inputs and outputs needs to be explored: 1) For physical systems with determinism elements and limited value ranges, the classic experimental design methods (e.g., random sampling, full factorial and fractional factorial designs, and central composite designs) and modern experimental design methods (e.g., Group Screening Design, Space Filling Design) are often adopted as tools [17].2) For complex social systems with numerous uncertain elements and the random value space, the Monte Carlo method and the resampling methods play the important roles.

C. Module 3: Predictive Module-Meta Model of Artificial Society

Upon gathering the input and output data, an in-depth analysis can be performed to extract the underlying rules governing these relationships.The primary objective of this analysis is to enhance our ability to predict and control these relationships more effectively.To overcome the limitations of manual exploration and experimental design-based techniques, the field of machine learning offers a wide range of tools to build a nonlinear mapping from the input to the output of artificial society.The learned (potentially nonlinear) function (i.e., the meta-model ) can be thought of as an approximate representation of the input-output relationship of the original simulation model [18].

The meta-model approach attempts to directly predict the outcome of interest, but does not explicitly focus on the activity of identifying causality.Traditional prediction models focus on out-of-sample data that still adheres to the same statistical distribution.The emphasis here is to enhance the applicability of the prediction model in various environments, such as uncontrollable factors or intentional interventions.It also encompasses more extreme scenarios in entirely new situations, where input features are set to completely novel values that have never been encountered before.By comparing the predictions of the meta-model against the observed patterns in the artificial society evolution, the accuracy and reliability of the predicted outcomes can be effectively validated.Furthermore, by combining optimization techniques (such as exact or heuristic methods) with meta-modeling techniques, it provides a possible path to find the input parameter combination that maximizes or minimizes a specific feature of the output of the original simulation model.

IV.DESCRIPTIVE MODELING: IDENTIFICATION OF INFLUENCING FACTORS AND RESPONSE VARIABLES

In computational experiments, artificial society plays the role of descriptive modeling, which is the foundation for interpreting modeling and predicting modeling, used to define,measure, collect, and describe the relationships between variables of interest.This section mainly addresses two crucial questions: 1) How can real data be effectively utilized to create concise and realistic artificial society models, achieving a generative deduction process from data to models and then from models to data? 2) How to identify the influencing factors and response variables, especially when it involves the intelligent characteristics of the agents themselves?

A. The Self-Evolving Artificial Society: From Model to Data

The assumptions about complex social systems in traditional artificial society modeling are mainly based on expert knowledge.To verify these hypotheses, questionnaires can be designed, collection and statistics to provide data support for the model.With the emergence of new technologies such as social media, the Internet of Things (IoT), cloud computing,and particularly big data, we now have convenient access to various data related to social systems.Based on the results of these empirical studies, we can embed the domain model into the design of the artificial society model, so as to realize various human-like characteristics of agents.The data generated by artificial society mainly comes from the adaptive changes of agents, which are concretely reflected in three aspects:decision-making, learning behavior, and interaction.The details are as follows:

1)Decision and Behavior Data: The heterogeneity among agents encompasses variations in their attributes and decisionmaking mechanisms.Heterogeneity allows for the simulation of unsolvable multi-agent dynamic game processes, where each agent may adapt or change over time.In order to depict the human-like characteristics of agent behavior, agent modeling needs to consider the cognitive, emotional, and social factors of agents from the perspectives of psychology and behavioral science (Fig.3) [19].Prospect theory studies how people make decisions under uncertainty.It elucidates the possible decision criteria employed by the majority of bounded rational decision-makers and offers valuable theoretical support for modeling agents’ bounded rationality [20].These modeling mechanisms make agent behavior data more realistic.

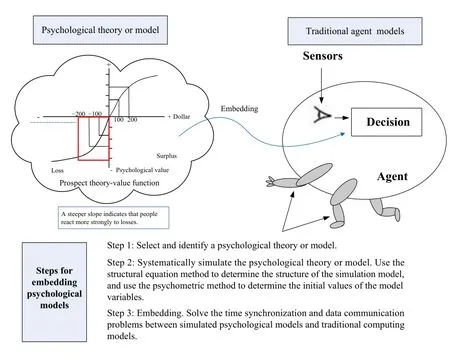
Fig.3.Psychological models embedding in ABM.

2)Learning and Evolution Data: In artificial society, there is no “top-down” or centralized control over individual behavior.The macro phenomena at timet+1 emerge endogenously through interactions among agents at timetor earlier.In the process, the learning ability of agents may need to be considered carefully.This typically involves characterizing agents’beliefs about environmental regularities, that is their “utility”functions, which guide their evaluation of the “expected” benefits associated with various behavior options.However,agents’ utility functions are not fixed but continuously adjusted based on action feedback through mechanisms like evolutionary learning, imitative learning, and reinforcement learning [21].The learning and evolution data of agents can exhibit the macro evolution trajectory of the system over an extended time scale, which can help to explain how a “complex system” is converted into a “complex adaptive system”.

3)Agent Interaction Data: The system modeling combining agent-based modeling with social networks is more flexible and can depict richer interaction rules between agents,which can be local, global, or a combination of both.The data obtained from generative deduction mainly includes three aspects:

i)Agent-centered data: The network plays an important role in the interaction among agents, but by changing input parameters unrelated to the network itself (such as agent states or policies), different model data can be obtained.

ii)Network-centered data: Agent remains its states unchanged, and the focus is on the impact of modifications at the network level on model data, such as changing the initial network density or size.

iii)Structural explicit data: Model data not only depends on agent or network attributes but also on the position of specific agents in the network, such as highly connected or loosely connected.

The traditional social data analysis only provides statistical depictions and is difficult to reveal internal process changes or the interaction of influencing factors.It remains limited to the induction of historical data and faces challenges in dynamically predicting intervention measures.In the past, individuals had to exert considerable effort to envision the outcomes of experiments conducted under different conditions, in diverse locations, or with varying participants.After the construction of artificial society models, researchers can directly use computational experiments to simulate and deduce these possibilities, achieving the transformation from models to data.

B. Determine the Influencing Factors and Response Variables

Computational experiments serve as simulated data generators, capable of deducing scenarios that may not have occurred in reality, and generating a mass of simulated data for specific problems [22].The state and behavior of a system are influenced by multiple factors and continuously undergo dynamic changes.Pareto’s principle (i.e., the 2-8 rules) [23]suggests that only a small number of factors are truly important.To comprehensively understand the problem being studied and reduce the simulation workload, it is essential to identify the key influencing factors and response variables before experiment design.The “multi-factor analysis method” is the commonly-used tool, which analyzes the impact of each factor by using the pattern “if a certain factor changes, how will the system’s state and behavior be affected”.This approach aids in gaining insights into the relationships and structures of complex problems, enabling better adaptation to uncertainty and change.

The whole analysis process is shown in Fig.4.In the top half of Fig.4, the structural equation model is frequently employed as a tool for organizing influencing factors and response variables [24].This model, in accordance with business logic, establishes logical connections among influencing factors, detailing their interrelationships and respective weights.In the lower half of Fig.4, the diagram adopts a fishbone-like structure.Here, the effects or response variables of interest are drawn along the central “spine”, while potential causes or design factors are arrayed along the “ribs”, aligning with the insights provided by the structural equation model.Furthermore, the process of selecting an experimental design is also depicted.This includes decisions on defining the purpose of the experiment, determining the number of repetitions,deciding the sequence of the experiments, considering whether to split the experiment into groups, and evaluating any other randomization constraints or factors that might be involved in the experimental setup.The key steps involved in determining influencing factors and response variables are as follows:

1)What Factors Affect the State And Behavior of the System?

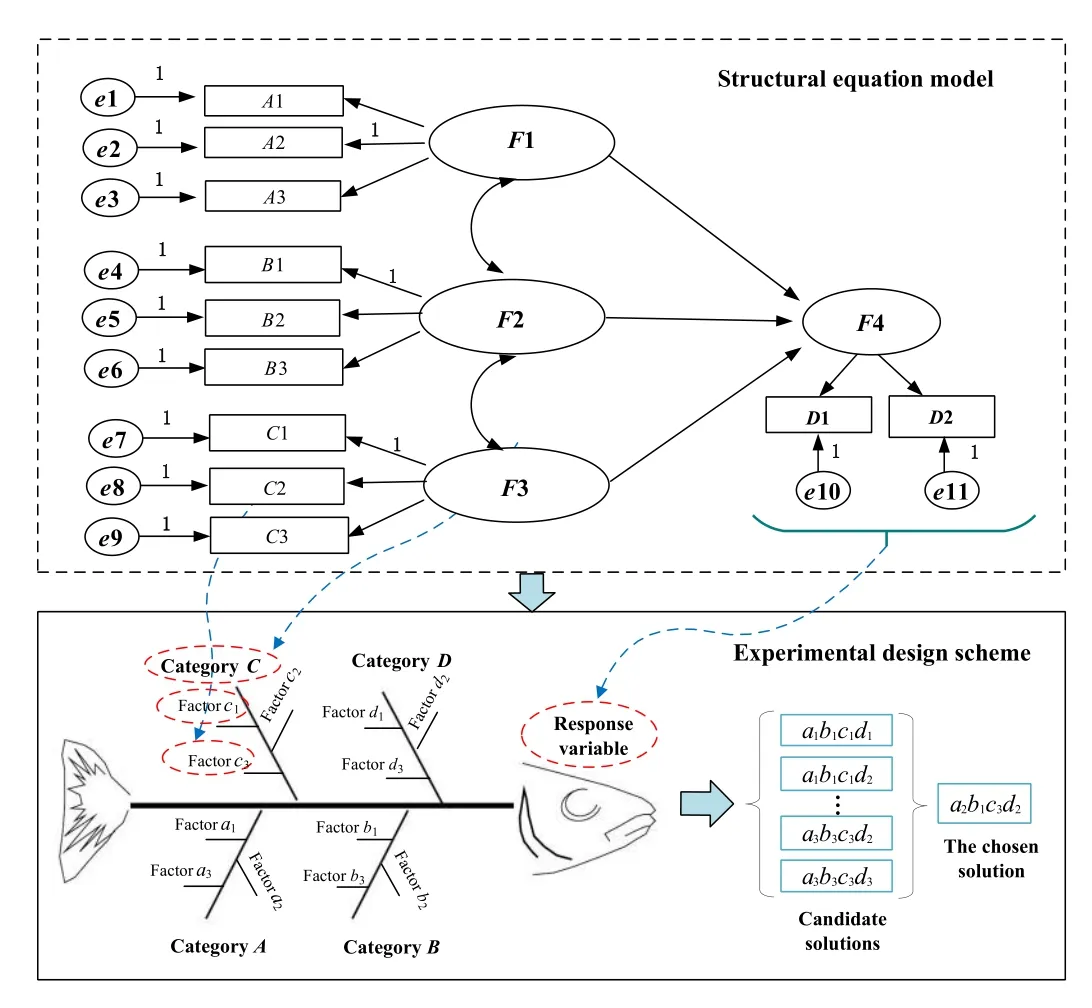
Fig.4.Selection of computational experiments design scheme.

The identification of factors influencing a system is a complex and crucial analytical process that requires deep thinking and comprehensive consideration of multiple aspects.The key is to comprehensively list the factors that may influence the state and behavior of the system.During this process, there may be interrelationships among different factors, where some factors have direct impacts while others have indirect impacts.The change in one factor can trigger a chain reaction, leading to changes in the system’s state.Additionally, influencing factors can intertwine to form a complex network of influences.Identifying influencing factors also requires considering their weights and priorities.Some factors may have more influence than others, so it is necessary to concentrate on the most critical factors.At the same time, we should also recognize that some factors are difficult to predict and control, such as the intelligence level of individuals or external regulatory strategies, but they can have significant impacts on problem-solving.

2)How to Design Appropriate Response Variables to Evaluate the Operating Status of the System?

The design of response variables needs to consider the following three factors: a) The inherent bias of measurements.Social systems are complex and multifaceted, and measurements are abstract and quantitative indicators taken to describe and compare system performance.In a sense, the results of measurements are bound to be partial and can only reflect partial facts.b) The tendency for local thinking in the measurement process.Response variables are designed to achieve system goals, but in practice, the selection of indicators for response variables often conflicts with goal optimization.c)The data interpretation of response variable must be based on the context.The same measurement data can lead to completely different results through different interpretations,which can be highly misleading.

3) How do These Factors Affect the State and Behavior of the System?

Understanding how each factor affects the system involves analyzing the pathways of influence (direct or indirect), the nature of the influence (positive or negative correlation), the degree of influence (how much impact it will have), feedback loops (the relationships between factors that can lead to complex feedback loops), and time delays (some factors may not have an immediate impact but take time to manifest).This helps to gain a deeper understanding of the mechanisms by which each factor operates.By conducting a more in-depth analysis, the focus of analysis can be traced back to further links in the chain of influence.In other words, it is important to consider not only the direct influencing factors but also the factors that influence those factors, and what influences those factors, and so on.By extending the chain of influence, it is possible to identify related or underlying factors that contribute to changes in influencing factors, helping to reveal the underlying causes of system changes.

V.INTERPRETATIVE MODELING: FACTORIAL EXPERIMENT DESIGN

By exploring the model’s response to changes in factors and the robustness of the model’s output to parameter uncertainties, we can gain a better understanding of the behavior and structure of the model.Factorial experiment analysis can be divided into two different methods: local analysis and global analysis.Local analysis involves changing the value of a single input variable and observing the changes in the model’s output.This helps understand the model’s response to individual parameters and determine which parameters have the greatest impact on the model’s output, known as the main effects of factors.Global analysis helps us understand the model’s response to multiple parameters, determining which combinations of parameters have the greatest impact on the model’s output.It also considers the interactions between different parameters, known as the interaction effects of factors[25].In computational experiments, the experiment design methods can be classified into two types: deterministic factorial experiment design and randomized factorial experiment design [26].

A. Deterministic Factorial Experiment Design Methods

Deterministic factorial experiment design refers to experiments where the factors and factor levels are known and can be controlled by adjusting the key factors.In a completely deterministic factorial experiment design, the factor levels are discrete, meaning that the values of experiment factors are divided into several segments.For example, a parameter can take on discrete values such asa1,a2,a3, and so on.Continuous factor levels, on the other hand, refer to experiment factors that have continuous values, such as [b1,b2].This is considered a special case of discrete multi-level research objects,allowing for more precise experiment analysis of the factors.However, it also involves a significant computational burden.

As shown in Fig.5, deterministic experiment design methods can be classified into the two types depending on the complexity of the research object: 1) Classical design methods:This method applies to cases where the experimental object consists of a few factors with limited levels.The input-output data of simulation experiments are typically analyzed using linear regression models represented by low-order polynomials.2) Modern design methods: The category of experimental objects include discrete multi-factor and multi-level, multifactor and low-level, low-factor and multi-level, and continuous factor level.These types of influencing factors are often more complex, resulting in combination explosion, which cannot be realized through simple combination and partial analysis design.

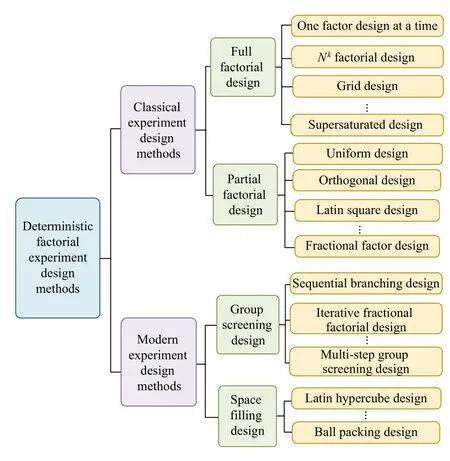
Fig.5.Selection of computational experiments design scheme.

The classical design method is further divided into partial factorial experiment design and full factorial experiment design according to whether all possible levels of all factors are analyzed.Details as shown in Table III.

Modern design methods have two categories: group screening design and space filling design.Group screening design was carried out by sequential experiment, that is, the selection of experimental factor levels was determined according to previous level selection and corresponding output.Space filling design is suitable for experimental situations where there is no random error, but the system bias is emphasized.When the concern of random error is much less than the model itself, the systematic bias, that is, the difference between the approximate model and the real mathematical function, should be of concern.The goal of space filling design is to limit system bias, and its test scheme can obtain ideal coverage, so as to lay a foundation for obtaining ideal experimental results data to provide decision support.The details are shown in Table IV.

B. Randomized Factorial Experiment Design Methods

When the input of an experiment system involves numerous uncertainties, the deterministic analysis methods may not be effective in finding a solution.In such cases, it becomes necessary to gain statistical insights into the experimental system by running the experiment repeatedly.Probabilistic sampling plays a crucial role in addressing the output response of experimental systems.Common random inputs are used to characterize the stochastic properties of artificial society.In scenarios with multiple completely random factors, the simulated dataset is also employed as output to observe the difference in system response.Determining the random data generation strategy that produces a dataset closest to the real situation becomes a key problem to be solved.Ideally, the data generation strategy should possess strong generalization capabilities, ensuring that the results of the computational experiment not only perform well in test scenarios but also provide reliable predictions for unknown scenarios.

When the distribution of factor levels is known, the Monte Carlo method is commonly employed to generate new datasets that follow the known distribution.Monte Carlo randomly extracts new (unobserved) datasets from the estimated population or data generation process, rather than from the observed dataset (like bootstrap).Monte Carlo method utilizes the probability density distribution of the scene parameters for sampling, generating randomized scenario test cases that closely resemble the true probability of occurrence.The basic steps of the Monte Carlo method are as follows: 1) Randomizing the problem of constructing or describing the probability of scene occurrence and representing the scene parameters as probability distributions.2) After constructing the probability model of scene parameters based on real scene data, sampling is performed from the known probability distribution, including importance sampling accept-reject sampling,Markov Monte Carlo sampling, and other complex distribution sampling methods.3) After sampling the known probability distribution, simulation is carried out to establish the scene parameter estimators.

Fig.6 gives a Monte Carlo simulation process of artificial society.In the upper half part of Fig.6, the scene is defined by three parameters: ParameterAfollows a triangular distribution, ParameterBfollows a normal distribution, and ParameterCis uniformly distributed.When utilizing the Monte Carlo method, random values are assigned to parametersA,B, andC, denoted as {ai},{bj},{ck} respectively.After that, countless simulation iterations are conducted, calculating the target response value as {ai+bj+ck}.By performing theNth simulation, the resulting distribution of possible scenarios can be obtained [27].

In the lower part of Fig.6, Event E occurs in a specific environment at the initial time pointr0.At the subsequent time pointr1, individual agents can decide their adaptive change according to restricted rationality to meet the challenges of the current environment, i.e., eventDadjusted byai.If they do not make a change (i.e., event ～D), the result isE, and so forth.Under the sequential logic model, the occurrence of the resultCis explained as one branching process that experiences multiple games and resolutions in the sample space Ω,i.e., one of the possible results.The emergence of resultCdepends on the simultaneous occurrence of necessary conditions (eventsD,A,Ware connected via AND), which has a significantly low probability.The occurrence probability of other results (failE,E∗, andE∗∗) is relatively high.

In reality, the distribution of parameter levels is often unknown.Such simulations inherently possess stochastic characteristics.For example, queuing problem is a typical random case, where the randomness of arrival or service times plays a significant role.In similar discrete event dynamic simulations, resampling methods are often used to generate datasets for experiments based on statistical patterns observedin historical data.If historical data is available for a specific time period, we can employ resampling techniques to generate new, unobserved datasets by repeatedly sampling from the observed data.Resampling can be either deterministic or random, depending on the specific method used.Deterministic resampling methods include jackknife (leave-one-out) and cross-validation (one-fold-out), while random resampling methods include sub-sampling (random sampling without replacement) and bootstrap (random sampling with replacement).Sub-sampling relies on weaker assumptions, however,it is impractical when the observed dataset has a limited size.Bootstrap can generate samples as large as the observed dataset, by drawing individual observations or blocks of them(hence preserving the serial dependence of the observations).The effectiveness of a bootstrap depends on the independence of the random samples, a requirement inherited from the central limit theorem.To make the random draws as independent as possible, the sequential bootstrap adjusts online the probability of drawing observations similar to those already sampled [28].

TABLE III CLASSICAL EXPERIMENT DESIGN METHODS

VI.PREDICTIVE MODELING: META-MODEL AND LAWS MINING

An essential objective of computational experiments is to uncover underlying patterns and laws within a system to realize its prediction and control.Once a combination of input parameters is obtained using sampling techniques in the design of the experiment, they are fed into the artificial society model, generating corresponding outputs.Through identifying of correlations among inputs and outputs of the system,the inherent patterns in the system are discovered, assisting decision-makers with valuable insights to solve practical problems.Contemporary data analysis tools, including data mining and regression analysis, offer powerful means to achieve law mining of complex social systems.

A. The Laws Mining Based on Meta-Model

A meta-model is a mathematical abstraction of the artificial society, which is used to describe the operation rules between input factors and response variables.Fig.7 illustrates how the simulation process of an artificial society is employed as a means of building meta-models.Firstly, various parameter combinations are inputted into the artificial society model,which then generates corresponding outputs through generative deduction.Within a defined experimental range, simulations at specific sample points are conducted, followed by the use of a simplified analytical expression (meta-model) to fit these results.Secondely, this meta-model is then subjected to a fitting validation, that is, the comparison of the extreme points.If the fitting validation is successful, the results derived from the analytical expression are considered equivalent to the results obtained from the simulation.Conversely, if the fitting validation fails, the corrective measures are taken,such as increasing the number of experimental points or narrowing the fitting range.

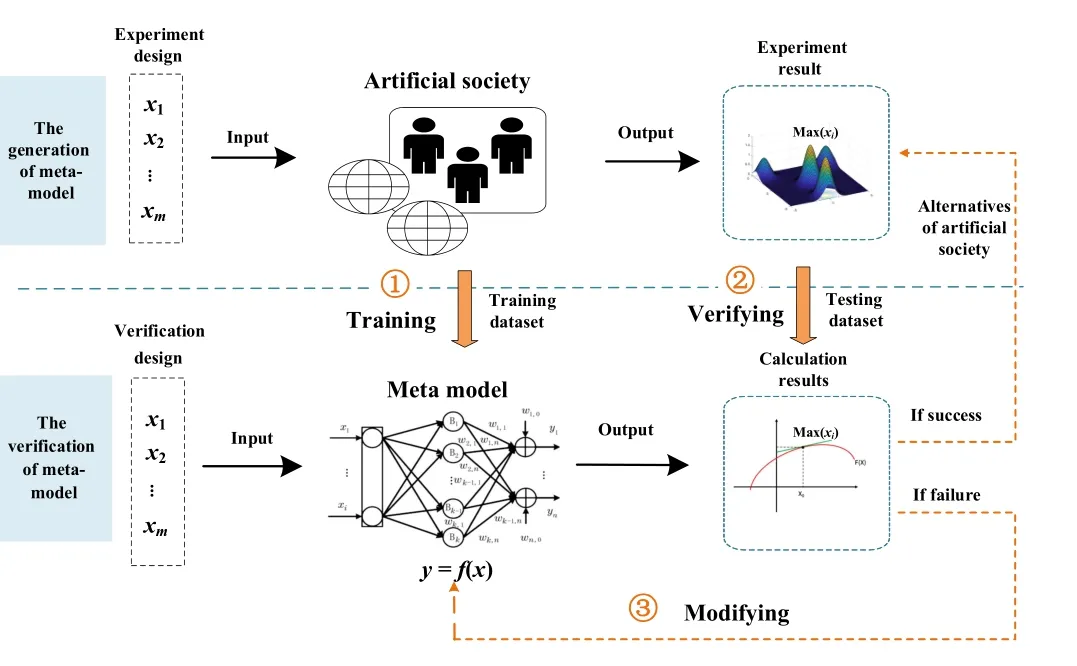
Fig.7.The verification and adjustment process of meta-model.

This process involves iterative cycles of simulation, fitting,and adjustment to achieve a satisfactory analytical expression.The reliability of the extreme points from the analytical expression hinges on the validity of certain assumptions.These include low-order interactions among model input parameters, low-order relationships between input parameters and output, and the residuals following a normal distribution.However, in the artificial society models, these assumptions are frequently challenged due to the highly nonlinear emergent behaviors, such as critical points, path dependence, and regime shifts.Therefore, careful examination is necessary to ensure these assumptions have not been violated when implementing this method [29].

With the increasing complexity of artificial society models,meta-model needs higher mathematical representation ability.Spatial statistical models and machine learning methods can be applied to learn functional relationships from the input to output of the simulated model, such as artificial neural networks, Kriging methods, support vector regression, random forests, multivariate adaptive regression splines, radial basis functions, and linear regression models, and so on [30], [31].Some common forms of meta-models are given as follows to represent the operating rules of the extracted system.

1) Statistical Model

The Kriging method [32], [33], also known as spatial correlation modeling, can be used to handle complex response surface structures.This model assumes that there is some spatial correlation among points in the multidimensional input space,and exploits these correlations to make predictions.The basic Kriging model can be expressed as follows:

where µ is the mean in the entire experimental area and δ (d) is the additional noise, which constitutes a covariance stationary process with mean 0.The main disadvantage of Kriging model is that the huge computational amount of parameter acquisition and the assumed spatial correlation is difficult to verify.

The parameter-free regression model does not rely on specific data distribution assumptions and is suitable for situations where the data distribution is unknown [34].The formal representation of the one-dimensional parameter-free regression model is as follows:

where ε is a random error,m(X)=E(Y|X) is called the regression function, here only assume that the function is a continuous function without introducing other parameters,compared to polynomial regression, the advantage of parameter-free regression model lies in its continuity.

2) Machine Learning Model

Compared with statistical methods, machine learning methods have higher requirements on data.Take the support vactor regression (SVR) [35] as an example.The goal of SVR is to find a hyperplane by constructing a regression model to fit the training sample as much as possible and try to avoid overfitting while keeping the prediction error minimal.The model function can be expressed as follows:

where ω=(ω1, ω2,...,ωd) is the weight vector of the input feature;bis the bias term.An “interval zone”ris created on both sides of the linear function, with a distance of ε ( i.e., the tolerance setting), which is usually determined through crossvalidation, and no loss is calculated for all samples that fall into the interval zone.The original problem of the SVR optimization target is not only to maximize the interval bandr, but also to minimize the loss to determine the parametersw,b.That is shown as follows:

whereξiand ξˆiare relaxation variables used to handle cases where data points fall within the boundary interval;Cis the penalty parameter used to control the weight of the error term;nis the number of samples.

By transforming the original problem with a constrained optimization into a Lagrangian unconstrained optimization function, the dual problem of the original problem is solved,and the final SVR model can be expressed as

Considering the nonlinear mapping ϕ(x), SVR uses the kernel function to map the input data to a high-dimensional feature space, which can easily get the dual form of the nonlinear support vector regression

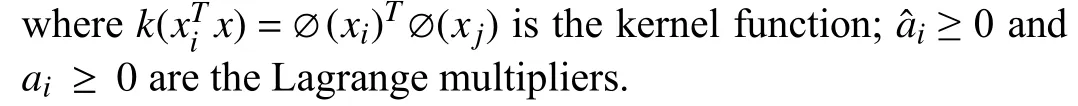
B. The Selection Method of Meta-Models

Statistical models are adept at identifying correlations between variables and are particularly beneficial in scenarios characterized by: 1) low levels of uncertainties, as they generally meet model assumptions like confidence intervals and hypothesis tests during their construction; 2) moderately sized datasets, excelling with fewer attributes but ample observations; 3) focusing on isolating the influence of a limited number of variables; 4) scenarios where a marginal error level in forecasts is acceptable; 5) situations with minimal interactions between independent variables that can be predetermined, and 6) contexts where explainability is prioritized over predictive accuracy.Commonly, statistical models implement parametric methods like linear and logistic regression.

Conversely, the primary aim of machine learning is to cultivate models that deliver consistent predictions, often at the expense of interpretability.These models require substantial data, including a vast array of attributes and observations, and are particularly suitable for: 1) outcomes with low randomness; 2) extensive training on numerous exact repetitions; 3)contexts where interpretability is secondary to achieving precise results, treating the model as a “black box,” and 4) scenarios without the need to isolate specific variable influences.Machine learning predominantly uses non-parametric methods such as K-nearest neighbors, decision trees, random forests, gradient boosting methods, and support vector machines (SVM).

Several studies have compared different performances of these techniques based on criteria such as accuracy, robustness, transparency (i.e., interpretability), and efficiency (i.e.,runtime) [36], [37].These studies indicated that support vector regression often yields the most accurate meta-models.Additionally, Villa-Vialaneixet al.[38] found random forests to produce more interpretable meta-models than support vector regression.

Support vector regression is favored for building meta-models due to its proficiency in representing nonlinear systems.Although it employs kernel functions to approximate highly nonlinear systems and generate accurate meta-models, this reduces the interpretability of the prediction function, rendering SVM a “black box” technique [39].The prediction function, while precise for unlabeled instances, does not offer direct interpretability.To enhance transparency, techniques that extract understandable rules, like IF-THEN rules, from prediction functions are available.However, rule extraction adds an abstraction layer, potentially leading to information loss.

Random forest (RF) is another viable technique for modeling input-output relationships in artificial societies.It is an ensemble model composed of numerous decision trees, represented as IF-THEN rules, and grown using the CART algorithm [40].Its training involves different bootstrap sets and a random subset of features for splitting at each node.These attributes reduce variance, making RF competitive in classification and regression [41].Rule selection algorithms in RF capture accurate and comprehensive rule sets directly, without additional abstraction, maintaining interpretability despite the model’s complexity.

When the output of artificial society models exhibits a unimodal distribution, the previously mentioned methods are generally suitable.However, in instances where the model’s output displays a multimodal distribution, particularly at critical points within the behavior space, the scenario changes significantly.Under these circumstances, meta-models that provide continuous estimates may not perform effectively.Metamodeling methods yielding classification outputs are more adept at accurately capturing the discrete jumps evident in the simulated model output.Consequently, it is imperative for analysts to initially ascertain whether the distribution of the simulated model’s output is unimodal or multimodal.This determination is crucial to fully leveraging the advantages offered by meta-modeling techniques.

VII.CASE STUDY: EXPERIMENT ANALYSIS OF DIGITAL DELIVERY PLATFORM

Currently, the scale of employment on internet platforms is unprecedented.Taking “Ele.me” and “Meituan.com” as examples, the number of registered delivery riders reaches millions.Internet platforms collect and analyze rider data, utilizing the findings to manage and organize labor within a digital system.While digital control significantly enhances labor efficiency, it also gives rise to social challenges such as “the balance between rider rights and platform efficiency”.In this section,computational experiments method is employed to study the social effects of algorithmic behavior causing “rider race”.This case demonstrates how to use the experiment design process proposed in this article and verify its validity.

A. The Description of Experiment Scene

Compared to the industrial era, workers on internet platform seem to have more “freedom” and “autonomy”.Platform workers have the flexibility to determine their own working hours, locations, breaks, and even the extent of their labor supply and wage levels, granting them a sense of work autonomy [42].In reality, as data-driven internet platform companies, they manage delivery rider teams by recording various details of rider’s activities.This new employment model and the platform’s control strategies rely on three core mechanisms: work autonomy mechanism, payment and incentive mechanism, and star rating mechanism.

On one hand, the platform system improves overall delivery efficiency by quickly assigning orders to riders, calculating estimated delivery times, planning delivery routes to guide riders, and providing various technological assistance during the delivery process (such as order heat-maps and estimated cooking times).On the other hand, the platform system precisely measures and calculates various aspects of the labor process, including rider location, ratings, acceptance rate,rejection rate, trip duration, and performance compared to other riders, enabling high-level control and accurate predictions of riders.

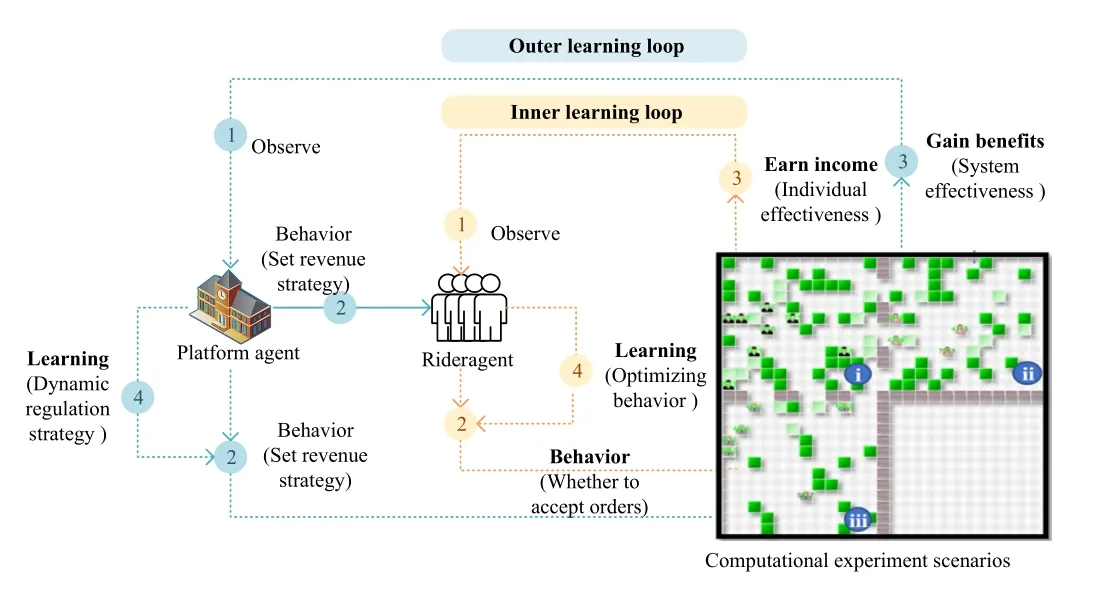
Fig.8.Experiment operation mechanism of internet delivery platform.

Fig.8 illustrates the operation mechanism of experiment system, which consists of the game between delivery riders and the platform algorithm.In this experiment system, the rider is an autonomous agent with learning ability, adjusting their behavior by learning to maximize their utility.The platform algorithm acts as a regulator, optimizing the overall system service utility by setting incentive mechanisms that consider both rider rights and platform efficiency.Table V provides the mapping relationship between the specific delivery scenario and the computational experiments system.

B. Experiment Target and Experiment Design

Based on the continuous game between the platform strategy and individual agents, the system operation may exhibit two tendencies.Firstly, the intensified competition may lead to severe harm to individual interests, rendering the system unsustainable.Alternatively, lacking of effective competition among individuals, resulting in poor overall system performance.Striving for a dynamic balance between individual interests and system performance, it becomes crucial to study the effects of different regulatory strategies on the system.In the comprehensive approach to design computational experiments outlined in this paper, the experiment design is structured around three key modules:

1)Descriptive Modeling

Illustrated in Fig.9, this module recognizes that various factors impact the effectiveness of platform strategies.These factors include the intelligence level of rider agents, the regulatory strategies implemented by platform agents, and the patterns of order occurrence, which constitute the environmental model.The primary response variables in focus are individual utility and system utility.

2) Interpretative Modeling

The design of the experiment involves configuring parameters for different combinations of influencing factors, relevant to the research questions.Distinct parameter combinations will yield varied experimental outcomes.This experiment,employing “one factor at a time” factorial experiment design methods, primarily investigates the effects of different platform incentive strategies on system utility.The platform’s reward strategy for rider agents encompasses “basic income”and “performance rewards”, with varying incentive strategies formulated by adjusting their ratio.

The experiment includes three experimental conditions:Free mode (Reward only), Equity mode (Income only), and Balanced mode (0.5 Income + 0.5 Reward).The Free mode acts as the control group, while the Equity and Balanced modes are experimental groups.The order sequence is gener-ated using Monte Carlo simulation, and repeated experiments are conducted to derive a mean value for data analysis.The study evaluates the impact of different regulatory strategies on the system using metrics such as the cost incurred by riders,rider’s revenue, and the number of orders completed.

TABLE V THE MAPPING RELATIONS BETWEEN REAL WORLD AND COMPUTATIONAL EXPERIMENT SYSTEM

Fig.9.The experimental design scheme of the case study.

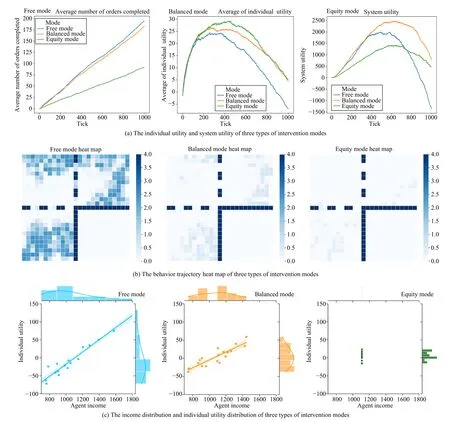
Fig.10.Experimental results of the scene.

3)Predictive Modeling

In this module, a linear regression model is employed as a meta-model for predicting system behavior, based on the input and output data from the artificial societies.The regression line’s slope indicates the relationship between rider agent’s income and utility.A strong correlation between these variables suggests increased competition within the system.Using the fitted meta-model, it becomes possible to forecast future competition intensity in the system.

C. The Analysis of Platform Strategies

According to the experiment design framework proposed in this paper, the experiment analysis is conducted from three aspects: description, interpretation and prediction.The experiment results are shown in Fig.10.

1)Descriptive Analysis: According to Fig.10(a), in terms of the number of tasks completed, Free mode > Balanced mode >Equity mode.In terms of individual utility, Equity mode >Balanced mode > Free mode.In terms of system utility, the balanced mode performs the best, as it can relieve over-competition between the riders while ensuring the continuous and rapid development of the platform system.In the first half of the experiment operation, the performance of the freed mode is better than equity mode.However, in the second half of the experiment operation, the performance of the equal mode exceeds the freedom mode.The result is caused by the significant decline in the individual utility of free mode.

2)Interpretative Analysis:As shown in Fig.10(b), in the free mode, the trajectory heat map of the rider agents shows the highest clustering effect.It indicates that the free mode can fully stimulate the rider agents to follow orders with higher earnings, reduce random exploration, and capture tasks purposefully and timely.Therefore, the movement trajectories show a high degree of overlap.In the balanced mode, the rider agents also exhibit a clustering effect.Except for a few blocks with darker colors, the other colors are lighter, indicating that the movement of the rider agents has both a certain degree of following and randomness.In the equity mode, the colors of the squares in the heat map are lighter, and there is no excessive overlap in the movement trajectories.This indicates that the agent’s movement has a certain degree of exploration and randomness, which also leads to a smaller number of tasks processed.

3)Predictive Analysis: As shown in Fig.10(c), in the free mode, the regression line has a larger slope, indicating a stronger correlation between agent income and utility.With the same increase in income, the increase in utility is relatively large.Therefore, the agent tends to pursue a higher income, leading to a high degree of competition.As a result,most rider agents concentrate in the lower left corner (low income and low utility).In the balanced mode, the slope of the regression line obtained is smaller, indicating a weaker correlation between agent income and utility.With the same increase in income, the increase in utility is not significant.Therefore, the proportion of agents pursuing income improvement is not as high, and the degree of competition is weakened, resulting in a more even distribution in various income intervals.In the equity mode, all agent income values are the same and have no correlation with utility.The utility value mainly depends on the agent’s own cost.Hence, the proportion of agents pursuing income improvement is very small,and the degree of competition is weak, mainly distributed in the interval where utility is greater than zero.

VIII.CONCLUSION

Computational experiments method provides a unique interpretative approach for analyzing complex social system,which includes generative inference and generative experiment.Generative inference, which is deductive, involves deducing macro rules from the initial configuration of agents.Generative experiment follows the principles of experiment methodology, including testing and selecting the initial set of rules.However, there is currently no systematic method for implementing abductive analysis for human and social factors in CPSS.This paper presents an integrated method for the design of computational experiments, which involves: 1) Determining the influencing factors and response variables of the system based on descriptive modeling of an artificial society;2) Identifying the relationship between influencing factors and macro phenomena by means of the factorial experimental design; 3) Building a meta-model that is equivalent to artificial society to explore its operating laws.

Although significant progress in relevant research, there are still many problems and challenges in the development of computational experiments method.For instance, while metamodels, as abstract structures generated from predictive models, can provide effective support for model analysis and processing, they face two problems.On the one hand, the discoveries generated by meta-models may lack replicability, and practical applicability.On the other hand, meta-models may be criticized for their limited generalizability, interpretability,and potential biases.By focusing on the potential power of causal inference, we may bridge the gap between the descriptive modeling (data analysis) and predictive modeling (meta model).Currently, although some scattered efforts have been made, there is still no systematic and mature method for causal inference based on computational experiments.Therefore, we will continue to conduct research in these areas, hoping to pave the way for advancements in computational experiments.