Adaptive Trajectory Tracking Control for Nonholonomic Wheeled Mobile Robots:A Barrier Function Sliding Mode Approach

Yunjun Zheng , Jinchuan Zheng ,,, Ke Shao ,,, Han Zhao ,Hao Xie , and Hai Wang ,,

Abstract—The trajectory tracking control performance of nonholonomic wheeled mobile robots (NWMRs) is subject to nonholonomic constraints, system uncertainties, and external disturbances.This paper proposes a barrier function-based adaptive sliding mode control (BFASMC) method to provide high-precision, fast-response performance and robustness for NWMRs.Compared with the conventional adaptive sliding mode control,the proposed control strategy can guarantee that the sliding mode variables converge to a predefined neighborhood of origin with a predefined reaching time independent of the prior knowledge of the uncertainties and disturbances bounds.Another advantage of the proposed algorithm is that the control gains can be adaptively adjusted to follow the disturbances amplitudes thanks to the barrier function.The benefit is that the overestimation of control gain can be eliminated, resulting in chattering reduction.Moreover, a modified barrier function-like control gain is employed to prevent the input saturation problem due to the physical limit of the actuator.The stability analysis and comparative experiments demonstrate that the proposed BFASMC can ensure the prespecified convergence performance of the NWMR system output variables and strong robustness against uncertainties/disturbances.

I.INTRODUCTION

IN recent decades, the control design of high-order nonlinear multiple input multiple output (MIMO) system has attracted much attention due to their wide applications in many fields, such as autonomous vehicles, unmanned aerial vehicles and intelligent robots [1].As typical high-order nonlinear MIMO systems, the nonholonomic wheeled mobile robots (NWMRs) play a vital role in environment exploration,industrial transportation and intelligent inspection and other fields owing to the characteristics of fast speed, high energy utilization, high interactivity and integration [2].However, the control performance of NWMRs may be considerably affected by time-varying uncertainties, such as parameter variation,external disturbance, and unmodeled dynamics.Besides,another main challenge faced by the NWMRs control design is the inevitable nonholonomic constraint which is not integrable and can not be eliminated in the mathematical model.Fortunately, in recent years, researchers have designed a variety of robust or adaptive control methods for NWMRs to deal with the time-varying uncertainties and nonholonomic constraint, such as sliding mode control (SMC) [3], [4], backstepping control [5], [6], model predictive control [7], [8], fuzzy control [9], learning control [10], [11] and adaptive control[12], [13], etc.Although these control methods achieve some outstanding performance for NWMRs, for instance, fast convergence rate, high accuracy, and robustness against uncertainties, they also have some drawbacks.For example, only asymptotic stability is guaranteed; estimating the finite time of error convergence is complicated; prior knowledge of uncertainties is employed, and a tremendous amount of computing is required.

Due to the excellent robustness, fast response and good transient performance, the SMC is considered as an effective tool for nonlinear controller design, which has been widely used in robot systems, such as robotic manipulators [14], actuated exoskeletons [15], bioinspired robots [16], and mobile robots [17].However, the SMC is not flawless.Once a more considerable switching gain is selected to suppress the unknown uncertainties and disturbances, the severe control chattering will emerge, even leading to the actuator saturation and energy loss.Furthermore, if uncertainties and disturbances increase to some extent that exceeds the ability of the selected switching gain, then the sliding mode will be lost, and errors will increase accordingly.The control chattering in mechatronic systems may cause severe deterioration resulting in undesired overshoots, oscillations, and instabilities.To alleviate the control chattering, several techniques have been developed, such as boundary layer technique (BLT) [18], filter technique [19], high-order sliding mode control (HSMC)[20], and adaptive SMC (ASMC) [21].The BLT is a classic approach to eliminate chattering by adopting a boundary layer around the switching surface, yet it compromises performance and chattering.Besides, a prior knowledge of the uncertainties bounds is still needed to ensure the stability of SMC.The filter technique alleviates the control chattering by softening the discontinuous control input and generating a continuous equivalent control input [22].However, similarly to BLT, it also requires the information of uncertainties bounds, and the control performance is sensitive to filter time constants.The HSMC solves the chattering problem by redesigning the sliding mode surface.In [23], a fast nonsingular terminal sliding mode (FNTSM) is proposed to achieve the tracking control of a linear motor with a finite-time zero-convergence property.In FNTSM, the switching element is replaced by a continuous function, which makes the FNTSM control (FNTSMC) chattering-free in nature [24].However,the converging neighborhood size relies on the prior knowledge of the uncertainties bounds.In ASMC, an adaptive control algorithm (ACA) is introduced to adapt the switching gains with respect to uncertainties and disturbances.Hence,the relatively small control gains are generated to suppress uncertainties and disturbances, which ensures the SMC with little control chattering.Nevertheless, the overestimation issue may occur when ACA estimates the unknown uncertainties and disturbances.

Since the ASMC method combines the attractive properties of both SMC and ACA, it has attracted a great deal of researchers’ attention recently, and some interesting research results have been applied to the trajectory-tracking control of NWMRs.For example, an extended state observer-based ASMC is proposed in [25] to estimate the aggregate uncertainty of NWMRs online with a PID-type sliding surface.Nevertheless, it can only guarantee asymptotic trajectory convergence for NWMRs as time tends to infinity.In [26], a fuzzy integral ASMC is employed to compensate for the lumped uncertainty of NWMRs with fuzzy logic.However,the complicated structure using membership functions and rules must be evaluated, resulting in a higher computational load for execution.A neural dynamic model-based ASMC for NWMRs is proposed in [27] to ensure the global asymptotic stability of the tracking errors without the prior knowledge of uncertainties bounds.Although the neural network scheme significantly alleviates the control chattering in SMC, the complexity issue of the controller and learning algorithm severely limits its practical application.In [28], an adaptive FNTSMC is developed to achieve the finite-time stabilization of the trajectory tracking errors for NWMRs.However, the tracking errors under this method can only be guaranteed with uniformly ultimate boundedness.The ASMCs mentioned above share the idea of using ACA to estimate the lumped uncertainty and applying SMC to counteract time-varying uncertainties and disturbances.Furthermore, some things could be improved for these controllers in reality.First, the ACAs in these controllers are designed in a gain-increasing form.More specifically, the control gains increase monotonically to be sufficient for solving the reaching phase and are locked at fixed values.When the amplitudes of uncertainties and disturbances become small, the control gains can not follow the variations.Thus, the control gains may be overestimated, which results in larger chattering and control magnitude.Second, the settling time and convergence domain are unpredictable, though some methods theoretically guarantee finite-time zero-convergence of the tracking errors.Moreover,the convergence properties rely on the initial conditions and the knowledge of the lumped uncertainty, which is unknown in reality.

Several solutions have already been proposed to solve the overestimation problem in ASMC with the first/second order sliding mode.Talebet al.[29], [30] and Utkin and APoznyak[31] have designed the first/second-order ASMC for the uncertain MIMO nonlinear systems with time-varying control gains defined in piecewise function form.The piecewise function-based ASMC (PFASMC) algorithms allow control gains to increase (or decrease) versus the variations of the uncertainties and disturbances without overestimating the switching gain and with guaranteeing the finite-time convergence of sliding mode variables to a neighborhood of zero.However,these approaches could be further enhanced.The adaptive schemes of these controllers have only been applied to the first/second order sliding mode, namely, no results of the adaptive scheme for high-order sliding mode.Besides, the size of the convergence domain and time rely on the bounds of the uncertainties and perturbations.Recently, the barrier function(BF) has been applied for the first-order SMC as a novel modality of adapting control gains [32], [33].In [33], a BFbased ACA makes the control gains follow the absolute values of uncertainties and drives the sliding mode variables to reach a prescribed neighborhood of zero in a finite time.Nevertheless, it is also imperfect that when the sliding mode variables approach the zone boundary (i.e., the vertical asymptote of BF), the control inputs step to infinity, leading to an actuator saturation problem.

Motivated by [29], [33], we propose a BF-based ASMC(BFASMC) strategy for the trajectory tracking control of NWMRs subject to uncertainties and perturbations.By adopting the BFASMC, the chattering and overestimation problem can be effectively mitigated without compromising the control performance, and the actuator saturation problem can also be avoided.The comparative experiments are conducted on a real NWMR platform between the BFASMC and compared controllers, i.e., FNTSMC, PFASMC and adaptive sliding mode dynamic control (ASMDC) [34].The experimental results demonstrate the superior performance of the proposed BFASMC in terms of faster convergence rate, higher tracking accuracy and better robustness.The main contributions of this paper are as follows:

1) The dynamic model of the NWMR formulated with uncertainties and disturbances is presented with novel error dynamics to serve the BFASMC design.Owing to the advantages of the novel error dynamics, the under-actuated problem and singularity problem are solved for the NWMR control system.

2) A BFASMC is presented to ensure that the NWMR tracking errors fast converge to a predefined neighborhood of zero with a predefined reaching time despite uncertainties and disturbances.Thanks to the advantages of BF, the requirements for the uncertainties and disturbances bounds and the overestimation of control gain are eliminated during the reaching phase and adaptive phase.

3) A modified BF-like control gain is designed to prevent the actuator saturation problem and retain the specified transient and steady-state performance, i.e., predefined reaching time and error bound, for the NWMR.

Notations: Fors,f∈Rm,|s| d enotes [|s1|,...,|sm|]T,s>f(ors≤f) denotes all elements ofsare greater than (less than or equal to) those off.For the sake of brevity, the arguments of system functions may be omitted in the following sections.

II.PLANT MODELING

A typical NWMR platform applied in our experiment is shown in Fig.1(a).The simplified model of the NWMR platform is shown in Fig.1(b).In this model, suppose the mass center coordinate of the NWMR is located at the mid-point of the connection between the driving wheels, i.e.,Oxy.The position of the NWMR in the reference coordinateOXYis defined as χ=[x,y,θ]T, whereθis the angle between the forward direction andX-axis.vandwdenote the forward velocity and angular velocity of NWMR, respectively.τland τrdenote the torques of the left and right driving wheels generated by DC motors, respectively.Besides, 2bdenotes the distance between two driving wheels, andris the radius of the driving wheel.In this work, the anti-clockwise direction is defined as the positive direction.The kinematic model and dynamic model of NWMR are given by [35]

Due to the pure rolling and non-slipping assumptions of NWMR, a nonholonomic constraint is imposed on it, i.e.,Aχ˙=0.Taking the time derivative of (1), it yields

Substituting (3) into the dynamic model (2), we obtain

Multiplying both sides of (4) byHTyields

Obviously, theHsatisfies the following equations:

By (5) and (6), the dynamic model (2) can be rewritten as

III.TRAJECTORY ERROR DYNAMICS

To formulate the trajectory tracking control problem, a reference trajectory for the NWMR is defined as follows:

Remark 1: The novelties of new error dynamics (17) are that it translates the under-actuated original dynamical model(14) into a fully-actuated one to facilitate the controller design, and avoids the singularity problem of the controller law which will be discussed in Remark 5.

Assumption 1: Suppose the lumped uncertaintydis timevarying and unknown, but the bound ofdexists under the following property:

IV.BFASMC DESIGN

This section proposes a BFASMC strategy for the uncertain NWMR system to achieve accurate position tracking with predefined reaching time and prescribed precision.

A. Preliminaries of BF

Fig.2.Schematic diagram of BF.

B. Controller Design

First, design a nonsingular terminal sliding manifold(NTSM) [23] as

C. Time Scale Transformation

D. Stability Analysis

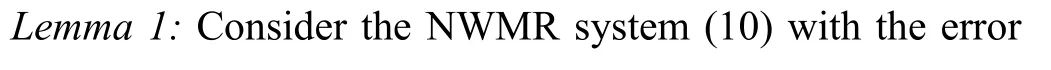
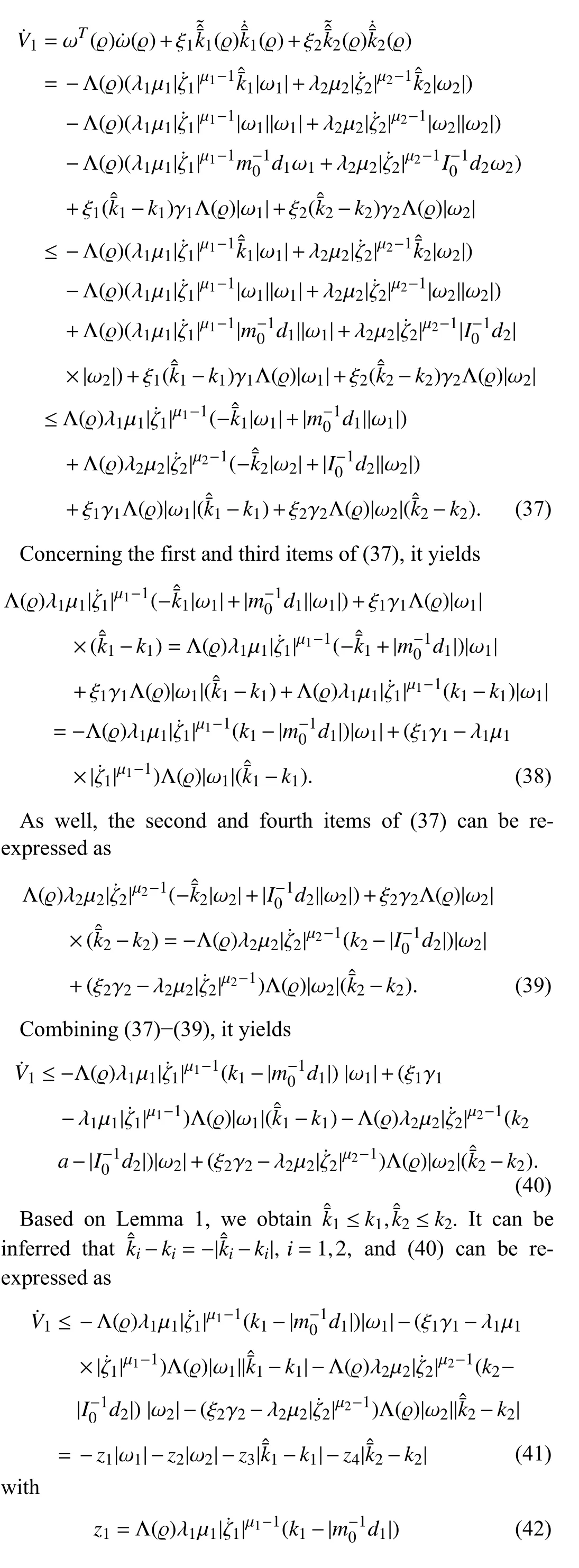
Remark 8: The results of Theorem 1 introduce two features of the proposed controller.First, the designed control gain matrix ϕAguarantees the finite-time stability of the sliding dynamics and error dynamics.It ensures the system trajectory converges to a predefined region with a prescribed reaching time, which suits many mobile systems that demand specified tracking accuracy and settling time.This feature makes the BFASMC different from the control method of [39], which only guarantees the time-varying bound of system trajectory with indistinct reaching time.

V.MODIFICATION AND IMPROVEMENT OF BFASMC

Based on Assumption 3, it can be inferred that σ1,2satisfy the finite-time stabilization condition [38].Hence, theσ1,2will converge to the region (-hi,hi) in a finite time.Furthermore, it can be obtained that

Remark 9: The foregoing discussion indicates that the BFASMC (27) with the ϕA(22) and the modified ϕB(64) possesses the capability of enforcing the σ1,2and ζ1,2to converge to region {|σ1,2|≤ρ1,2<η} and {|ζ1,2|≤2ρ1,2<2η},respectively.Even if σ1,2leave the region { |σ1,2|≤ρ1,2} due to severe disturbances, the modified BF-like control gain ϕBican still guarantee the finite time stability and prevent the actuator saturation problem.

Remark 10: From the above analysis, the designed control scheme (27) with the adaptive strategy (22)-(26) and the modified BF-like control gain (64) has the following advantages: i) removal of the requirement for uncertainties and disturbances bounds during the control design, ii) elimination of overestimation of adaptive control gain leading to less control chattering and vibrations, iii) explicitly predefined bounds for the tracking error and reaching time, and iv) prevention of the input actuator saturation.

Furthermore, the designed control scheme is worthy of going into further development.For example, the convergence time and tracking accuracy can be further optimized using the heuristic optimization approach [41]; the undesirable chattering in control input could be alleviated by integrating fuzzy control scheme.

VI.PARAMETERS DESIGN OF BFASMC

The anticipated control performance in the practical application involves accuracy, response speed, robustness, signal chattering, and control effort.In order to acquire a more balanced system performance, this paper provides a design guideline of the BFASMC parameters, which also facilitates the usage of this control method.

1)Selections ofλ1,λ2andµ1,µ2: From the sliding mode function (19), we know that λ1,2and µ1,2critically dominate the sliding mode dynamics performance, such as convergence rate, tracking accuracy and control chattering.The smallerλ1,2and larger µ1,2lead to a faster convergence rate and higher tracking accuracy ofebut at the cost of amplifying the measurement noise and control chattering.In experiment,λ1=4.1, λ2=4.2, µ1=1.9, µ2=1.9.

VII.EXPERIMENTAL RESEARCH

To demonstrate the capability of the proposed BFASMC,we implement the verification experiments on a real NWMR test platform displayed in Figs.1(a) and 4.The NWMR system contains a main body supported by two driving wheels,two auxiliary wheels and some essential electrical devices,including a real-time microcontroller, a Li-polymer battery,two motor drivers (Maxon ESCON-36/2), and two DC motors(Maxon 118391) (equipped with encoder to measure the rotary angle) driving wheels to achieve autonomous motion.The controller (27) is first programmed in MATLAB 2021a environment to verify the validity with the numerical simulation of the NWMR system.Afterward, the proposed controller is programmed in the LabVIEW software and implemented on a real-time NI microcontroller with a sampling time of 10 ms to drive the real NWMR.The system inputs,i.e., the posture signals of the NWMR, are calculated using a posture estimator with the motor encoder signals.The nominal parameters of the NWMR arem0= 45 kg,I0=0.56 kg·m2,b=0.188m,r=0.042m.Since the payload is the main parameter uncertainty for the NWMR system, a3 kg payload is fixed at the NWMR platform to test the robustness against parameter uncertainty.The recently presented control methods, i.e., FNTSMC [23], PFASMC [30], and a widely adopted NWMR control strategy, i.e., ASMDC [34], are also carried out as the compared controllers.

A. Comparative Controllers

Fig.4.Test platform.

For a fair comparison, the sliding manifolds for PFASMC and FNTSMC are the same as that in BFASMC (27), which results in the equivalent control inputs of PFASMC and FNTSMC are consistent with the τ0(20).This subsection introduces only the reaching control inputs of PFASMC and FNTSMC.All parameter values of the compared controllers are carefully tuned to achieve the ideal tracking performance for the NWMR system.

1)PFASMC: The reaching control of PFASMC is

B. Experimental Results and Analyses

To illustrate the performance metrics of the proposed BFASMC for NWMRs, we conduct two experiments with respective scenarios, i.e., with initial position offset and external shock disturbance.Besides, the NWMR platform is mounted with a 3 kg payload for all experiments.A circular reference trajectory for the NWMR is designed as follows:

namely, the radius is 0.6 m and angular speed is 0.7 r ad/s.The initial posture is set asx(0)=-0.1,y(0)=-0.1, θ(0)=0,which makes the initial conditions of σ1,2satisfy|σ1,2(0)|≥η/2 , and experiment duration is set as 20 s.In order to analyze the experimental results more accurately, it is important to define some nomenclatures, such as the root-mean-square of error (RMSe) , the maximum value of error (MAXe) and accumulative error (Ae).The mathematical forms of these nomenclatures are as follows:

wherendenotes the sample number,eidenotes theith sampled error and ∆tis the sampling period.The statistical results ofRMSe,MAXe, andAeare summarized by Table I in which some superior values are highlighted in boldface.

1)Trajectory Tracking Control With Initial Position Offset:This experiment verifies the tracking performance and robustness of the controllers with an initial position offset and payload.In Fig.5, it can be found that the outputs of the sliding mode variables σ1,2under BFASMC meet the desired tracking performance illustrated in Theorem 1.Specifically, the σ1,2converge to the set {|σ1,2(t)|<0.025} before the time upper boundTp=1.5 s, and the trajectories of σ1,2are contained in the set {|σ1,2(t)|<0.05} for all future timet≥1.5 s.The tracking results of position profiles and tracking errors under the three controllers are shown in Figs.6 and 7.It can be found that the BFASMC has the fastest convergence rate,and the settling times of tracking errors under BFASMC are 0.95 s, 1.19 s and 1.35 s which are 185.2%,583.3%,551.3%;213.7%,712.4%,541.2% and 375.7%,273.9%,167.4% faster than those of FNTSMC, PFASMC and ASMDC, respectively.The rapid convergence rate of BFASMC can be attributed to the sliding mode function (19), the time-varying gain φ (t) (25)and the proportional termkˆ with the adaptive laws (24).Besides, the steady-state errors (SSEs) under BFASMC are bounded in 0.0045 m, 0.0015 m, and 0.006 rad, which are smaller than those of FNTSMC, PFASMC and ASMDC.This is because the adaptive algorithm in BFASMC can estimate the uncertainties and disturbances bounds and avoid overestimating based on the BF structure.A similar conclusion can also be observed in Table I.TheRMSe,MAXeandAevalues of BFASMC are smaller than those of FNTSMC, PFASMC and ASMDC.Fig.8 illustrates the voltage inputs of driving wheels, which reveal the control input levels of the NWMR under the four controllers.It can be observed that the PFASMC and ASMDC have severe chattering instead of the less chattering in BFASMC and FNTSMC.The reason lies in the switching elements in the adaptive laws and reaching controls of PFASMC and ASMDC.In addition, the chattering of FNTSMC is smaller than that of BFASMC.This is because the usage of continuous function makes the FNTSMC chattering-free theoretically; however, the chattering due to noise is inevitable in experiment.

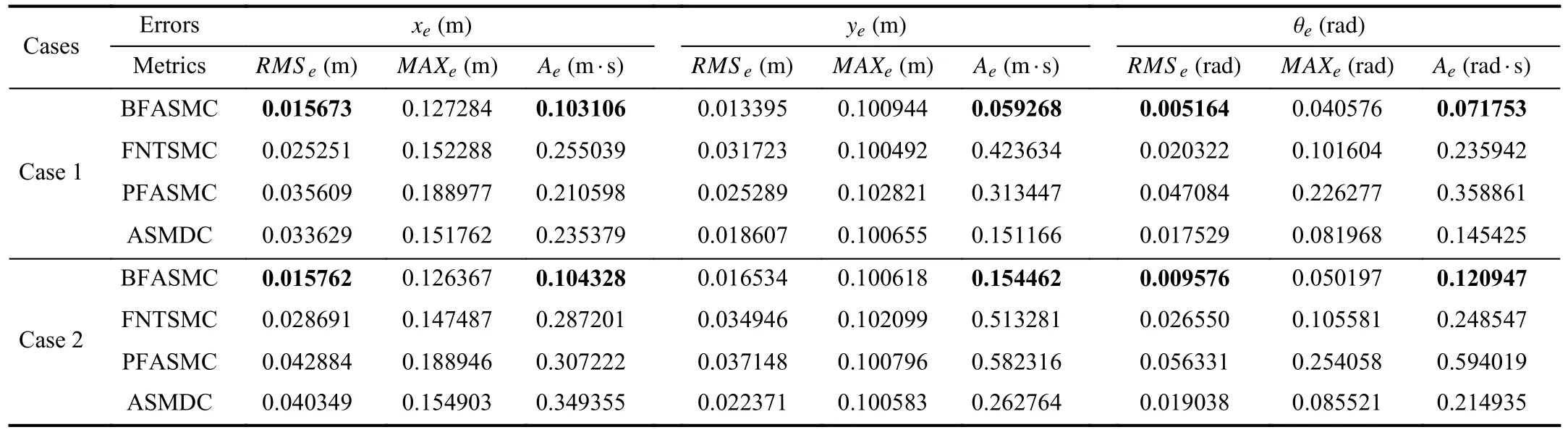
TABLE I TRACKING PERFORMANCE EVALUATION OF THE TWO EXPERIMENTS

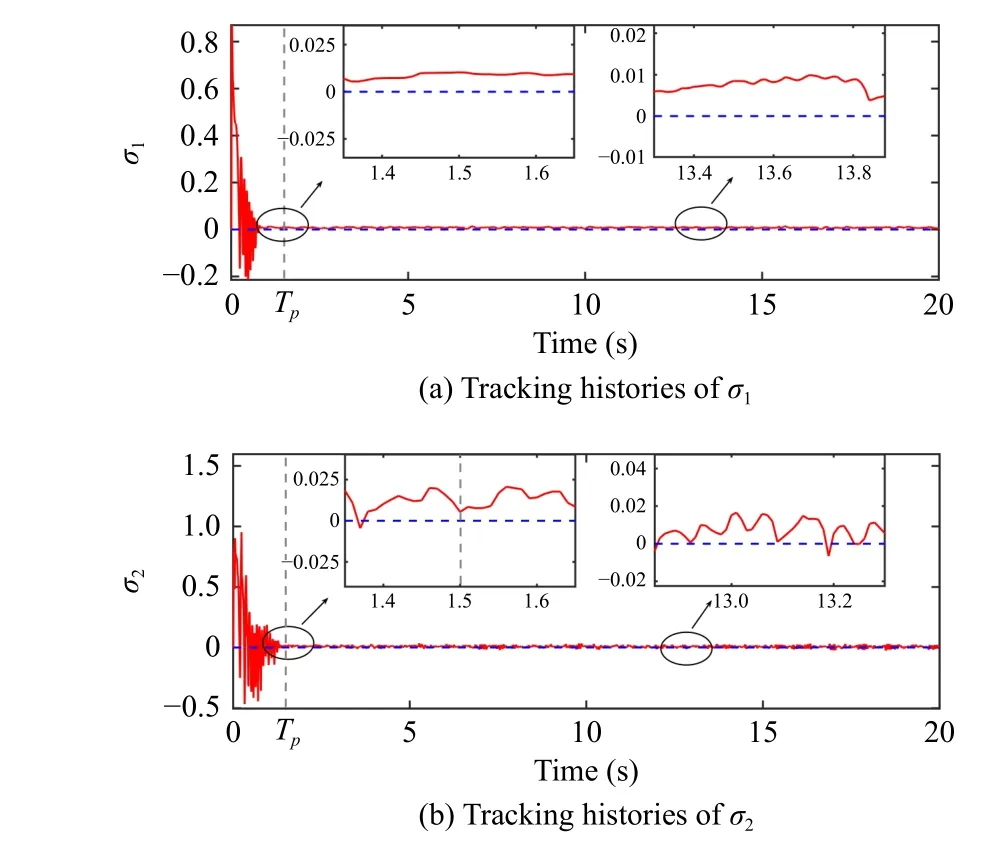
Fig.5.The trajectories of the sliding mode variables σ1,2 under BFASMC with an initial position offset.

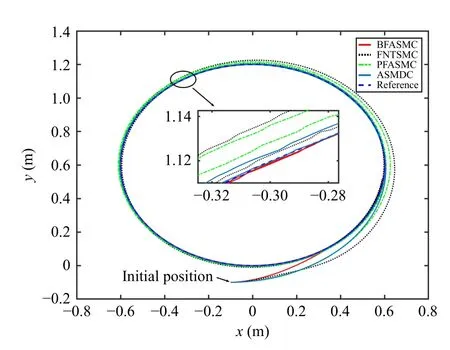
Fig.6.Comparative results of the trajectory tracking with an initial position offset.

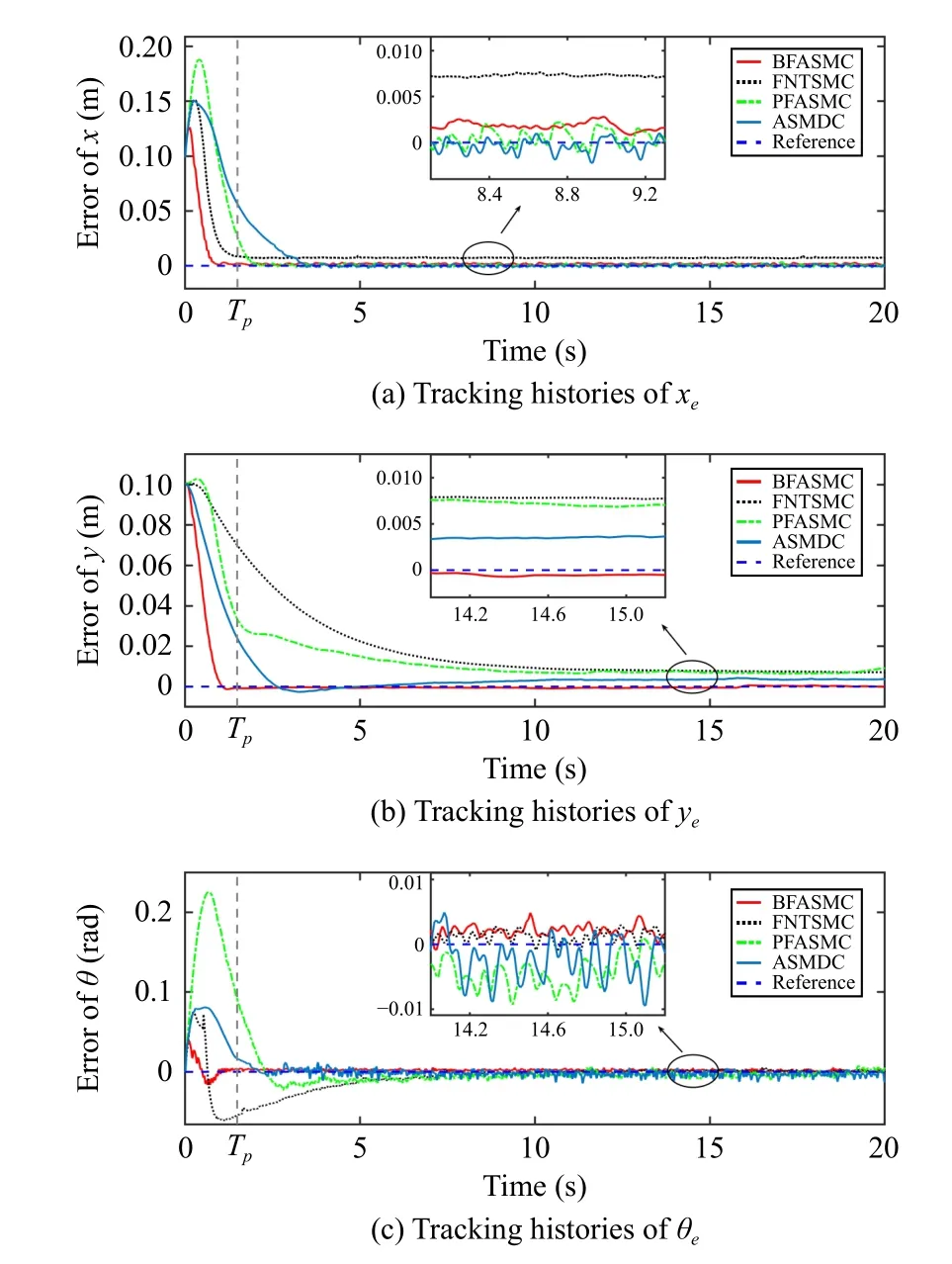
Fig.7.Comparative results of the tracking error e with an initial position offset.

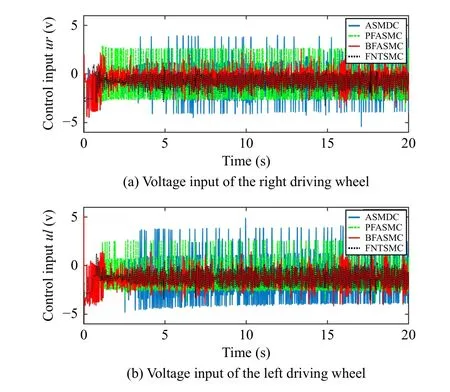
Fig.8.Comparative results of the control input with an initial position offset.

2)Trajectory Tracking Control With External Shock Disturbance: To verify the robustness performance of the proposed controller against the external disturbance, two half-sine waveform electronic disturbances δ1=δ2=5|sin(2πt)| are imposed in the control inputτ.The disturbances duration is 0.5 s, occurring at the 12th s when the NWMR system is stable.The trajectories of the sliding mode variables σ1,2under BFASMC are shown in Fig.9.It can be seen that the tracking responses of σ1,2escape from the steady state when the external shock disturbances occur.Since the control gain matrixΦ has been switched to the BF-based term ϕB, the control inputs increase rapidly to pull back the σ1,2to the origin due to the characteristics of BF.After the |σ1,2| decrease, the control inputs decrease accordingly to avoid overestimating control gains.This phenomenon verifies the performance features of the design adaptive mechanism and BF.From Figs.10 and 11,it can be found that the BFASMC takes a shorter time to make the NWMR return to steady state operation and retains the tracking errors in a desired level, i.e.,±0.0045 m,±0.0015 m,±0.006rad.Nevertheless, FNTSMC, PFASMC and ASMDC all have a significant degradation of the trajectory tracking and error tracking.The statistical results in Table I also confirm the effectiveness of the BFASMC to counteract the external shock disturbance.For instance, the increment ofRMSeunder BFASMC in this experimental case is smaller than those of the other controllers.The control signals illustrated in Fig.12 also verify the feature of BF, i.e., rapidly changing with respect to the external shock disturbance.In addition, it can be seen that the peak values of the control inputs after the shock disturbance under BFASMC are 3.17977 V and 3.17996V, which are 7 7.4%,75.9%; 7 4.6%,76.8% and85.6%,81.6%smaller than those of FNTSMC, PFASMC and ASMDC, respectively.This phenomenon demonstrates that the modified BF-like control gain can effectively prevent the actuator saturation; meanwhile, the specified tracking precision is guaranteed.

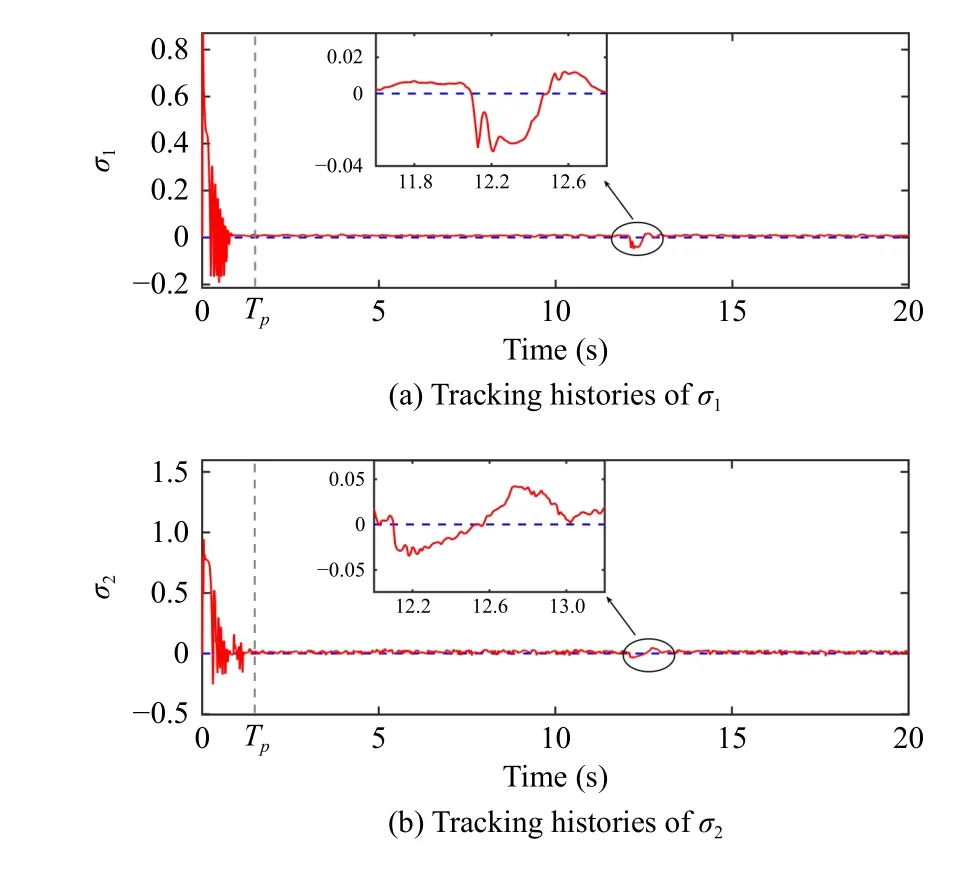
Fig.9.The trajectories of the sliding mode variables σ1,2 under BFASMC with external shock disturbance.

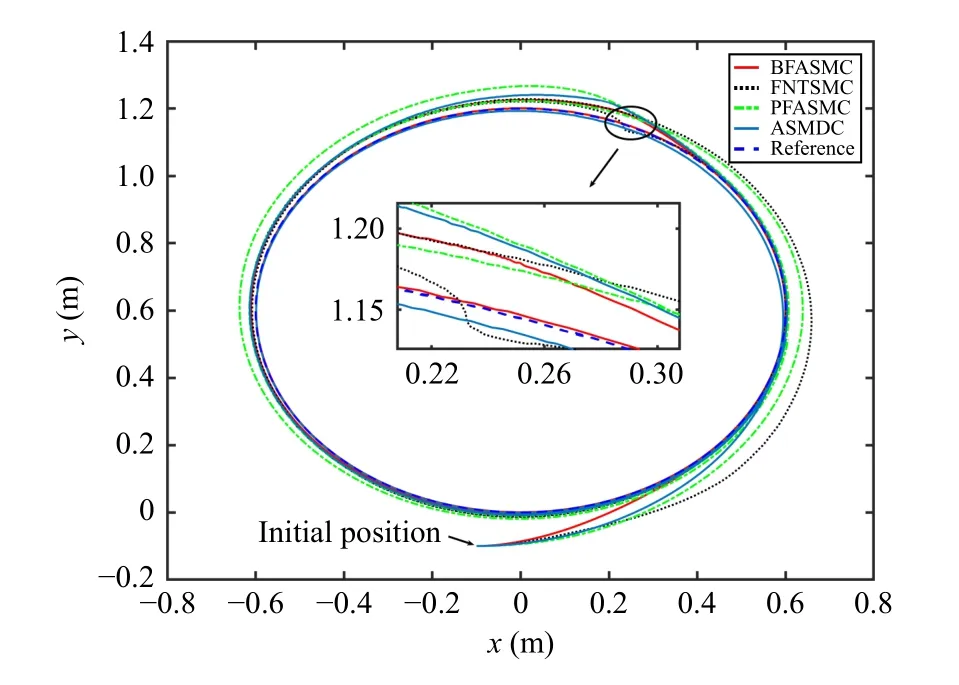
Fig.10.Comparative results of the trajectory tracking with external shock disturbance.

Fig.11.Comparative results of the tracking error e with external shock disturbance.

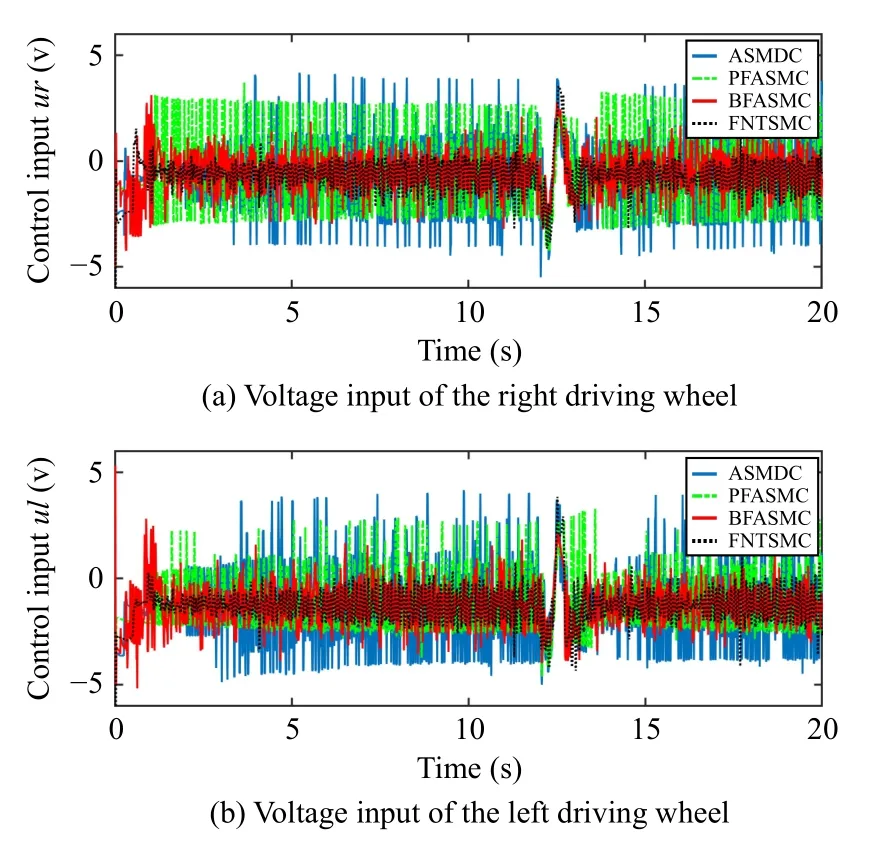
Fig.12.Comparative results of the control input with external shock disturbance.

VIII.CONCLUSION

This paper developed a BFASMC strategy for the trajectory tracking control of NWMRs in situations of external disturbances and parameter uncertainties.The proposed approach differs from the existing ASMC methods, which apply the monotonically increasing adaptive mechanism to suppress uncertainties and disturbances.The usage of BF in the BFASMC guarantees that the control gains can be adaptively adjusted to follow the change of disturbances, i.e., control gains increase (decrease) as disturbances increase (decrease),resulting in the elimination of gain overestimation.On the other hand, the suggested approach ensures that the sliding mode variables converge to a prescribed neighborhood of zero in a predefined time, independent of the initial condition and uncertainties bound.As a result, the NWMR system output variables, i.e., tracking errors, can converge to a prescribed region near zero with a shorter settling time.Besides, the developed modified BF-like control gain resolves the actuator saturation problem for the existing BF-based control methods.Finally, the comparative experimental results on the NWMR platform confirm the superior properties of the developed BFASMC.

The future work of our research will include further improving the control performance of the proposed BFASMC by integrating with the heuristic optimization approach; integrating the proposed BFASMC with fuzzy control scheme to alleviate the chattering in control input.

APPENDIX A

APPENDIX B