Path-Following Control With Obstacle Avoidance of Autonomous Surface Vehicles Subject to Actuator Faults

Li-Ying Hao ,,, Gege Dong , Tieshan Li , Senior,, and Zhouhua Peng , Senior,

Abstract—This paper investigates the path-following control problem with obstacle avoidance of autonomous surface vehicles in the presence of actuator faults, uncertainty and external disturbances.Autonomous surface vehicles inevitably suffer from actuator faults in complex sea environments, which may cause existing obstacle avoidance strategies to fail.To reduce the influence of actuator faults, an improved artificial potential function is constructed by introducing the lower bound of actuator efficiency factors.The nonlinear state observer, which only depends on measurable position information of the autonomous surface vehicle, is used to address uncertainties and external disturbances.By using a backstepping technique and adaptive mechanism, a path-following control strategy with obstacle avoidance and fault tolerance is designed which can ensure that the tracking errors converge to a small neighborhood of zero.Compared with existing results, the proposed control strategy has the capability of obstacle avoidance and fault tolerance simultaneously.Finally, the comparison results through simulations are given to verify the effectiveness of the proposed method.

I.INTRODUCTION

WITH the expansion of applications in military actions,fishing, marine environmental monitoring, search and rescue, maritime safety and so on [1]–[3], autonomous surface vehicles (ASVs) have attracted intensive research [4]–[6].There are some control techniques being studied including trajectory tracking [7], dynamic positioning [8], path following[9], etc.

Path following is a common motion control problem[10]–[13].In [14], an algebraic implicit path was introduced to design a path-following controller, which is divided into speed control and heading control.Reference [15] adopted a parametric path to design an output feedback path-following controller.ASVs usually sail in challenging sea environments,and the occurrence of actuator faults is practically unavoidable.Actuator fault is one of the challenging issues associated with the path following control of ASVs, which may result in terrible performance or the cancellation of tasks [16]–[19].Hence, it is essential for ASVs to have certain fault-tolerant abilities, which has motivated researchers to investigate this problem [20]–[22].Control allocation is an effective approach for achieving fault tolerance against actuator faults.In [23],the actuator fault was modeled as a change of constraint input matrix.Reference [24] designed a fault-tolerant control scheme to compensate for offshore vessels system.Considering partial faults, a fault-tolerant model predictive control strategy [25] was proposed.However, only a few type of faults such as the partial loss of effectiveness and bias fault are considered in the above works.As a matter of fact, multiple types of actuator faults may occur in the meantime for ASVs.There exist marine plant twisters in complex marine environments, and the occurrence of the stuck fault is inevitable.Therefore, it is essential to consider a more general actuator fault model including the stuck fault for ASVs.References [26], [27] constructed a general fault model to solve the fault-tolerant control problem for dynamic positioning of a ship.However, the above fault-tolerant control was proposed based on the linearized model of the ship, and the problem becomes more complex when the nonlinear model of ASVs is taken into account.To enhance the ability of fault tolerance for ASV, dealing with more general types of actuator faults is valuable.Hence, designing a path-following control strategy of ASV in the framework of a more general actuator fault model including a stuck fault is the first motivation of this paper.

In complex marine environments, there exist various obstacles which will affect normal operation and even threaten the safety of ASVs.Therefore, obstacle avoidance capabilities are of primary concern for the safe sailing of ASVs.Determining how to achieve obstacle avoidance has resulted in significant research [28]–[31].Many efficient obstacle avoidance methods have been proposed including prescribed performance techniques [32], artificial potential function methods [33],fuzzy logic methods [34] and so on.The advantages of artificial potential function methods include having a simple structure, less adjustment parameters and real-time collision avoidance.Thus, it is widely used in practice [35]–[37].A mobile robot can bypass obstacles by using an artificial potential function method [35].The issue of unmanned aerial vehicles collision avoidance in [36] was solved using the potential function method.Considering the movement of obstacles, [37]constructed a positive potential function for unmanned aerial vehicles capable of obstacle avoidance.In addition, the artificial potential function was often used to design formation control for ASVs [38]–[40] employed the repulsive potentials to avoid collisions with obstacles.Note that all the aforementioned results were developed without considering the occurrence of actuator faults.When taking actuator faults into consideration, the current obstacle avoidance strategy may become ineffective.Hence, determining how to develop a path-following controller that can compensate for actuator faults and has the capability of obstacle avoidance is another motivation of this paper.

In view of the above discussions, this paper aims to develop a path-following controller with obstacle avoidance and fault tolerance for ASV subject to model uncertainty, external disturbances.The following main contributions are concluded.

1) Considering actuator faults and obstacle avoidance simultaneously, the path-following control scheme with obstacle avoidance and fault tolerance is developed which can ensure the uniform ultimate boundedness of tracking errors.

2) The actuator fault effect on existing obstacle avoidance strategy is revealed.As the lower bound of actuator efficiency factors decreases, the safe obstacle avoidance distance becomes smaller.In other words, the occurrence of actuator faults leads to the conservativeness of the traditional obstacle avoidance strategy.

3) To compensate for actuator faults, an improved artificial potential function is constructed by introducing the lower bound of actuator efficiency factors.The proposed obstacle avoidance strategy can be reduced to an existing one in [38] in the absence of actuator faults.

In this paper, the sections are summarized as follows.Section II presents description and problem statement.Section III provides the path-following controller design and stability analysis.Comparison simulation results are shown in Section IV.Section V is the conclusion of this paper.

There are some notations below.//·// represents thel2-norm of a vector.λmax(·) and λmin(·) are the maximal eigenvalue and minimal eigenvalue of symmetric matrix, respectively.

II.DESCRIPTION AND PROBLEM STATEMENT

A. ASV Model

Considering the ASV equipping with actuators, the dynamics of ASV is described as [41]

whereη(t)=[x(t)y(t)ψ(t)]T∈R3represents the position and

R(ψ)∈R3×3heading of ASV.is expressed as

Remark 1: Compared with the parametric path in (4), a nonparametric path [14] can ensure the invariance of the path.However, this paper considers fault-tolerant control for the fully actuated ASV in the framework of control allocation,which does not need to control speed and heading separately.Therefore, the parametric path to design path following control strategy is adopted in this paper.

B. Actuator Fault Model

In complex marine environments, actuator faults inevitably occur.We consider the actuator fault model [42] as follows:

whereu(t)∈Rmdenotes the control input signal, andϕis defined as ϕ=diag{ϕ1,...,ϕi,...,ϕm} whereϕis a semi-positive-define weighting matrix, and its elements satisfy

whereχ is an unknown positive constant.

Assumption 2:rank (Gϕ) = rank (G) holds for allϕ ∈∆ϕj,j=1,2,...,j=1,2,...,L.

Remark 2: It is natural to assume that the stuck fault or bias fault is bounded.Assumption 2 indicates that actuators are redundant, which is significant in compensating for stuck faults.

C. Problem Formulation

To develop the path-following control strategy with obstacle avoidance and fault tolerance, the following tasks should be satisfied.

1)Geometric Task: The ASV moves along a predefined path.A small positive constantp1exists such that

2)Dynamic Task: The update velocity of the path variableϑconverges to expected path update speedvs(t), that is

wherep2∈R is a small positive constant.

3)Obstacle Avoidance Task: In the presence of obstacles,ASV can avoid collision and maintain sailing safely

wherep(t) andpk(t) denote the position of the ASV and thekth obstacle, respectively.∈R is the smallest safe obstacle avoidance distance.

III.PATH-FOLLOWING CONTROLLER DESIGN AND STABILITY ANALYSIS

A. Improved Artificial Potential Function

Considering that the actuator faults and obstacle avoidance occur simultaneously, we construct a new artificial potential function as follows:

Remark 3:Compared with the existing artificial potential function in [38], we improve the artificial potential function by intro ducing actuator information φk.When there is no actuator fault, φk=1, i.e., the artificial potential function can be reduced to the existing result [38] in the fault-free case.The proposed artificial potential function considers the occurrence of actuator faults, and is capable of obstacle avoidance in this case.

B. Nonlinear State Observer Design

The nonlinear state observer is employed in this part to estimate the model uncertainty and disturbances.And the ASV dynamics (1), (2) can be rewritten as follows:

where ζ(t)=M-1[-C(ν)ν(t)-D(ν)ν(t)-g(ν,η)+ω(t)] represents model uncertainty and external disturbances.In addition,the nonlinear state observer requires the following assumption.

˙ζ(t)

Assumption 3:is bounded, that is

where ζ∗is a positive constant.

In Assumption 3, ζ (t) is a vector as the function of velocity.Moreover, the control inputs and the energy of external disturbance are bounded, so it is reasonable to make the above assumption.

The following nonlinear state observer is designed for estimating the model uncertainty and external disturbances:

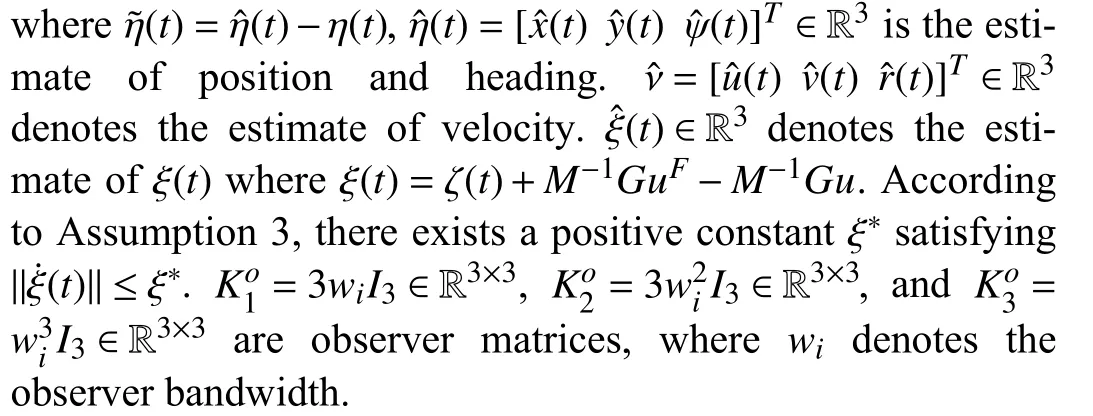
The observer error dynamics can be obtained as follows:

where

Based on the above nonlinear state observer, the stability analysis of the error dynamics (17) is shown as follows.

Lemma 1: In the case that Assumption 1 holds, the observer error dynamics (17) is input-to-state stable, and the error signals satisfy the following inequalities:

and

where γ1=([ϖ(1-ρ)]/[λmax(Q)]) and 0 <ρ<1 provided that

C. Path-Following Controller Design and Stability Analysis

The controller is designed so that obstacle avoidance and fault tolerance can be achieved.To facilitate the controller design, our previous result in the subsequent lemma [42] is introduced, which is shown here to guarantee the completeness of the results.To simplify the representation, the state variabletis omitted from the relevant functions in this section.

Lemma 2:Assuming Assumption 1 is true, a known positive constant φ exists such that the following inequality is satisfied:

where it holds for all ϕ ∈∆ϕj,j=1,2,...,j=1,2,...,L.

The position error vector is defined as follows:

whereR=R(ψ) , η ∈R3is the position of the ASV.

From (1) and (2), the derivative ofz1is given by

Letvs-δ(t)= ϑ˙(t), then we have

Step 1: To design the path-following controller with obstacle avoidance and fault tolerance, we design a kinematic control law νcas follows:

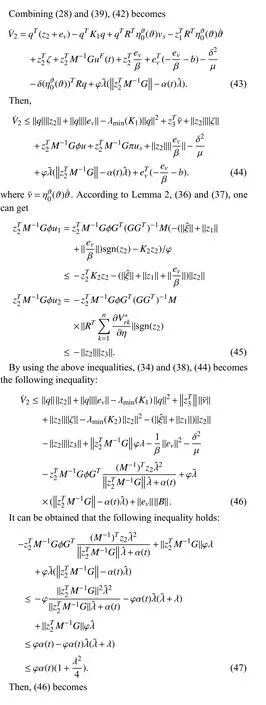
Next, the stability of the cascade system made up of the nonlinear state observer error subsystem and path following control error subsystem is described.

Theorem 1: Under the precondition of Assumptions 1 and 3,the path following control strategy with obstacle avoidance and fault tolerance can be designed.Besides, the all error signals in the cascade system are uniformly ultimately bounded.Take into account the ASV dynamics in (1), (2), as well as the nonlinear state observer (14), the proposed controller (28),(35)-(38) and the path update law (32), we can obtain the above conclusion.

Proof: Firstly, outside the obstacle avoidance range, we verify the stability of the cascade system.By applying Lemmas 1,3 and [46, Lemma 1], we obtain that the cascade system is input-to-state stable.||ζ||-||ξ||, ξ˙ and //B// are bounded.There exists a positive constant ϵ satisfying ||ζ||-||ξ||≤ϵ.So we can obtain that | |E1|| is uniformly ultimately bounded satisfying

IV.SIMULATION RESULTS

To verify the effectiveness of the proposed control strategy with obstacle avoidance and fault tolerance, Cybership II is used to simulate the scenario in this section.The corresponding parameters of Cybership II and the equipment of the actuator can be obtained in [47].G∈R3×5is an actuator configuration matrix of ASV and its parameters are given in [41].Then the actuator configuration matrix is

Fig.1 shows that the ASV moves along a parametric path,and the proposed control strategy is capable of obstacle avoidance and has fault tolerance.Fig.2 demonstrates that the surge, sway, yaw velocities of ASV can be estimated precisely.Fig.3 shows that uncertainty and external disturbances are estimated by using the nonlinear state observer.From these figures, we can observe that the nonlinear state observer can accurately address the model uncertainty and external disturbances where only measurable position information of ASV is used.To illustrate the effectiveness of the proposed strategy, this paper compares the existing results without considering actuator faults.Figs.4 and 5 illustrate the comparison results through simulations.The comparison velocities of ASV system are drawn in Fig.4.Fig.5 depicts the comparisons responses curves of tracking error.We can see that the proposed control strategy can not only compensate for actuator faults and ensure obstacle avoidance but also accomplish the tasks in (7)-(9), when obstacle avoidance and actuator faults occur simultaneously.

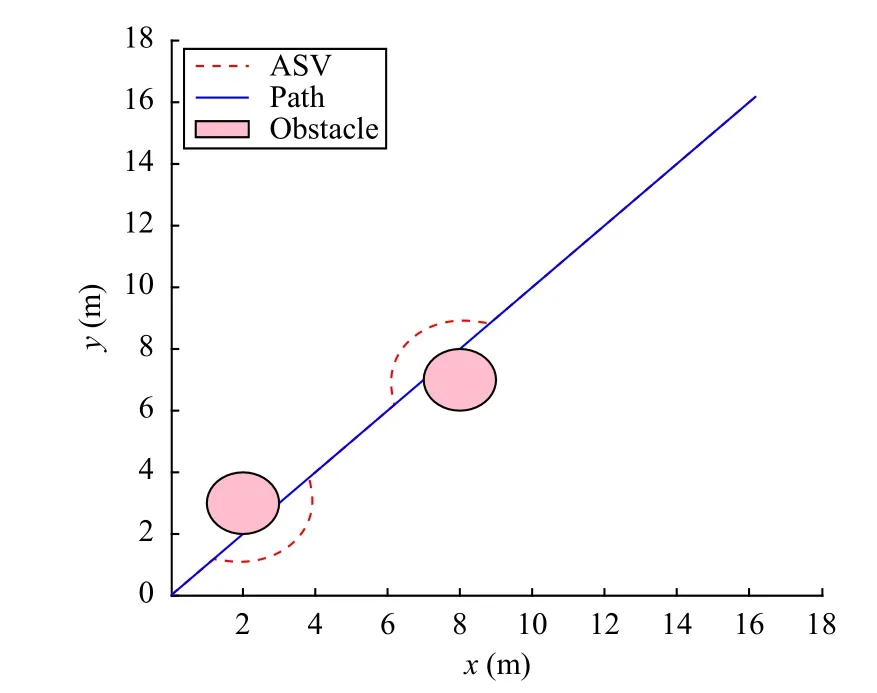
Fig.1.The effect of path following control strategy with obstacle avoidance and fault tolerance.

V.CONCLUSION

This paper presents the path-following control strategy with fault tolerance and obstacle avoidance for ASV.First, the nonlinear state observer is utilized to address model uncertainties and external disturbances, which only depends on measurable position information of ASV.Considering the occurrence of actuator faults, an improved artificial potential function is constructed by introducing the lower bound of actuator efficiency factors.Furthermore, the upper bound of the stuck fault is estimated using an adaptive mechanism.Then, based on the backstepping technique, a path-following controller with obstacle avoidance and fault tolerance is designed to compensate for actuator faults, and ensure the tracking performance and suppress uncertainty and external disturbances.It is verified that all signals are bounded.Finally, the efficacy of the proposed control strategy is shown through simulation.

Fig.2.The estimation of velocities using the nonlinear state observer.

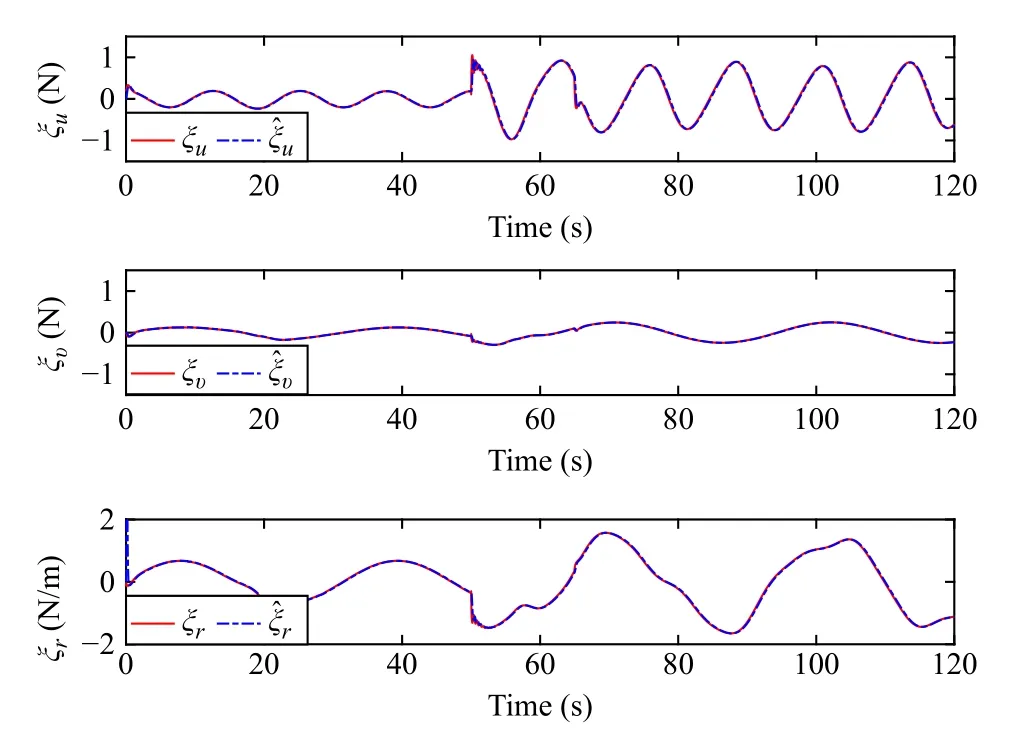
Fig.3.The estimations of disturbances using the nonlinear state observer.

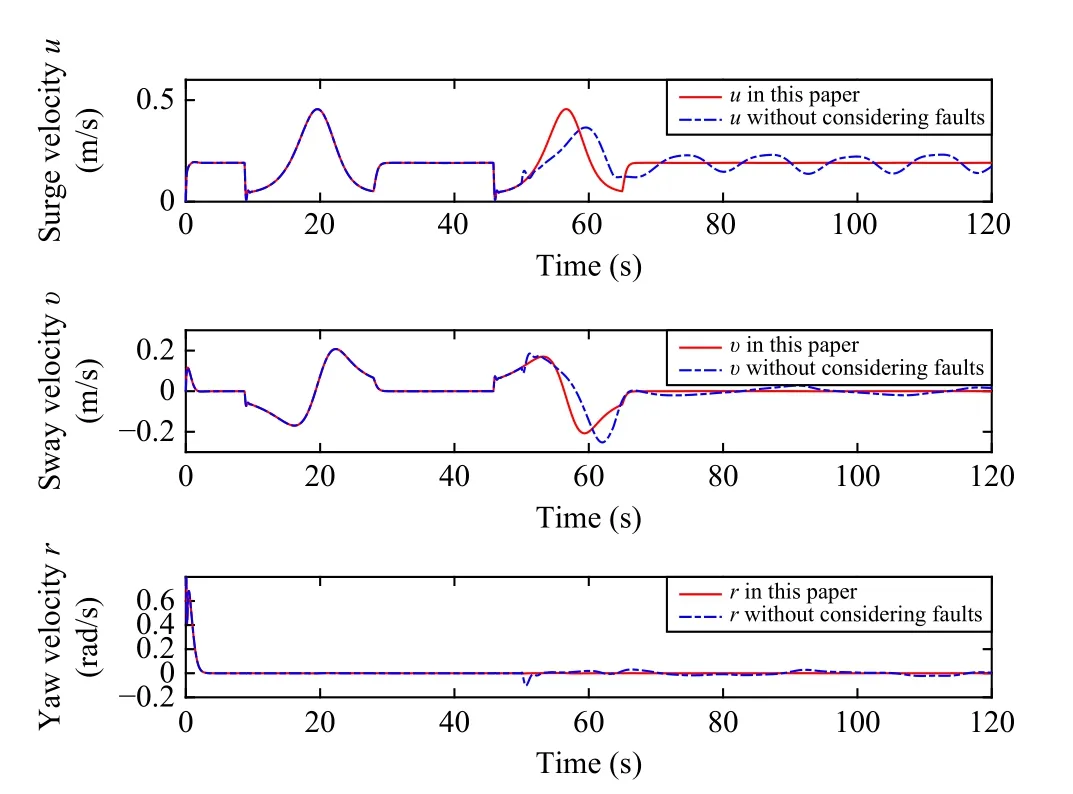
Fig.4.The velocity comparisons of the ASV.

Fig.5.The tracking error comparisons.