Quantization and Event-Triggered Policy Design for Encrypted Networked Control
2024-04-15YongxiaShiandEhsanNekouei
Yongxia Shi and Ehsan Nekouei
Abstract—This paper proposes a novel event-driven encrypted control framework for linear networked control systems (NCSs),which relies on two modified uniform quantization policies, the Paillier cryptosystem, and an event-triggered strategy.Due to the fact that only integers can work in the Pailler cryptosystem, both the real-valued control gain and system state need to be first quantized before encryption.This is dramatically different from the existing quantized control methods, where only the quantization of a single value, e.g., the control input or the system state, is considered.To handle this issue, static and dynamic quantization policies are presented, which achieve the desired integer conversions and guarantee asymptotic convergence of the quantized system state to the equilibrium.Then, the quantized system state is encrypted and sent to the controller when the triggering condition, specified by a state-based event-triggered strategy, is satisfied.By doing so, not only the security and confidentiality of data transmitted over the communication network are protected, but also the ciphertext expansion phenomenon can be relieved.Additionally, by tactfully designing the quantization sensitivities and triggering error, the proposed event-driven encrypted control framework ensures the asymptotic stability of the overall closedloop system.Finally, a simulation example of the secure motion control for an inverted pendulum cart system is presented to evaluate the effectiveness of the theoretical results.
I.INTRODUCTION
A. Motivation
NETWORKED control systems (NCSs) are ever-present in our societies by enabling critical systems and services such as intelligent transportation and smart grid systems.NCSs heavily rely on information and communication technologies for their operations [1].However, the widespread usage of communication networks and untrusted computing entities, e.g., cloud-based controllers, makes NCSs more vulnerable to cyber-attacks [2].For example, an adversary with access to sensor measurements of an NCS can easily extract sensitive information about the system.Therefore, it is crucial to address the security vulnerabilities of NCSs.
The homomorphic encryption (HE) technique [3] provides a promising solution for the security of NCSs as it permits computations using encrypted sensor measurements without access to the actual measurements.Using HE, the sensor measurements of an NCS can be shared with untrusted computing entities over communication networks.In this case, even if the transmitted data, including sensor signals and control input,are eavesdropped by a malicious adversary, their actual values still remain unknown to the adversary.
However, the common HE cryptosystems, such as ElGammal, Rivest-Shamir-Adleman (RSA), and Paillier, can only encrypt positive integers.Thus, any data required for computing the control law in an NCS must be quantized before encryption.However, quantization results in strong nonlinearity in the system, yielding system performance degradation and even instability.Moreover, HE methods suffer from ciphertext expansion, which undoubtedly increases the size of data transmitted over communication networks.Cyphertext expansion is a great challenge for NCSs due to their inherent resource limitations in terms of computation, communication,and storage [4].For instance, the high data rate requirement of HE cryptosystems might result in heavy channel congestion,thereby resulting in delays and packet dropouts.
B. Contributions
In this paper, we develop quantization and event-triggered policies to address the quantization and ciphertext expansion challenges of HE-based encrypted NCSs.The main contributions are three-fold:
1) A novel dynamic quantization policy with a state-dependent sensitivity is presented.Different from traditional uniform quantizers with fixed sensitivity, which only ensure that the system state converges to a neighborhood of the equilibrium, the proposed quantization policy ensures asymptotic convergence of the system state.Besides, unlike uniform quantizers with time-varying sensitivity, the proposed dynamic quantization policy does not require an extra time sequence to update the sensitivity, which circumvents potential conflicts between sensitivity updating and triggering communication.
2) By defining a quantization-related measurement error, the adverse effect of quantization errors is implicitly considered in the event-triggered strategy, which contributes to a rigorous analysis of the inter-event time interval.Moreover, an adjustable factor is introduced into the triggering condition,ensuring the validation and availability of the event-triggered strategy.
3) An event-driven encrypted control framework is proposed using the Paillier cryptosystem, modified static and dynamic quantization policies, and the quantization-related event-triggered strategy.The strong nonlinearities caused by quantization and event triggering, including two coupled errors, are tactfully compensated by selecting proper parameters.It is shown that under the proposed event-triggered encrypted controller, the closed-loop system is secure and asymptotically stable.
C. Related Work
HE-based encrypted control of NCSs has been studied in[5]–[10].A pioneering encrypted control scheme was proposed in [5] to enhance the security of NCSs, based on multiplicative HE of RSA and EIGamal.Different problems related to HE-based encrypted control of NCSs have been studied in the literature, e.g., quantizer design and stability analysis [6],[7], observer-based encryption[8], and overflow/underflow of encrypted data [10].In particular, the quantizer design problem was first addressed in [6] and then was extended in [7], in which a stability-guaranteed dynamic ElGamal cryptosystem was developed.Furthermore, using the additively HE method,an encrypted distributed state observer was presented in [8], to enhance the privacy of the measurement data and estimated state.Kimet al.[9] provided a practice implementation over homomorphically encrypted data in an infinite time horizon using a dynamic feedback controller.To eliminate the overflow/underflow issue due to encryption, a secure and private control approach was proposed in [10], wherein the controller is reset periodically.
The event-triggered control (ETC) method has been widely used to address the security of capacity-limited NCSs, such as faulty accommodation [11], anti-DoS attacks, deception attacks, sparse attacks [12]–[14], and privacy-preserving control [15].Moreover, the ETC scheme with quantized measurements has been extensively studied, especially using a uniform quantizer [16]–[19].For instance, by combining uniform quantization and the ETC strategy, the leader-following consensus problems for linear and Lipschitz nonlinear multiagent systems were addressed in [17].Taking external disturbances into account, two high-gain control laws with quantized relative states were designed in [18] to ensure the bounded consensus using event-triggered quantized communication protocols.Xuet al.[19] studied a unified distributed control method for linear networked systems with various quantizers, where the uniform quantization effect was analyzed in detail.However, due to the fixed quantization sensitivity in [16]–[19], only uniformly ultimately bounded stability of the system was ensured even without the external disturbance.
What’s more, although a few researchers have studied event-based secure control issue of NCSs (like [11]–[15]), it is still rare to use encrypted networked control with the HE and ETC method, as it is in its infancy stage.Kishida [20] proposed a Paillier-type encrypted control scheme for the NCS using a uniform quantizer with a time-varying quantization sensitivity.Then, the proposed encrypted control law was extended to an event-triggered communication case.Later, the same event-triggered encrypted control problem was addressed in [21] using the ElGamal cryptosystem.Nevertheless,it should be pointed out that several deficiencies still exist in the existing event-based secure control schemes of NCSs, e.g.,potential conflicts between the quantizer and event-trigger updating and the nonzero phenomenon of the measurement error at the triggering time instant.
Inspired by the aforementioned discussions, we develop a novel event-driven encrypted control framework for NCSs,including two modified uniform quantization policies, the Paillier cryptosystem, and an event-triggered strategy.Remarkably, to construct the HE-based encrypted control law,we need to quantize the system state and the control gain simultaneously.If two uniform quantizers (e.g., [16]–[19]) are directly used to quantize them, the control performance of closed-loop system will be severely deteriorated due to strong nonlinearities stemming from coupled quantization errors.In particular, such an adverse impact on the system performance would be further aggravated in the triggering communication scenario.Therefore, these research results in [16]–[19] can not be directly applicable to the HE-based encrypted control framework.To address this challenge, we propose static and dynamic quantization policies for the control gain and system states, respectively.By carefully selecting the quantization sensitivities, the proposed quantization policies not only achieve the desired integer conversions, but also guarantee the asymptotic convergence of the quantized system state to the equilibrium.On the other hand, in contrast to the time-varying quantization policy in [20], our dynamic quantization policy does not require additional time instances to update the quantizer’s sensitivity.This is particularly important for practical implementations as it avoids potential conflicts between triggering communications and sensitivity updating.Additionally, we use the quantized system state to define the measurement error in the event-triggered strategy, which ensures the measurement error can be set to zero when specific events occur.Different from the event-triggered policy in [20], [21],the adverse effects caused by quantization errors are implicitly considered in the triggering condition, and a more rigorous analysis of the inter-event time interval is provided in our work.
D. Organization
The rest of this paper is organized as follows.Section II provides the preliminary technical background and formulates the encrypted control problem.Section III discusses the event-driven encrypted control algorithm, including the design of quantization and event-trigger policies.The simulation results are provided in Section IV.Finally, concluding remarks are given in Section V.
E. Notations
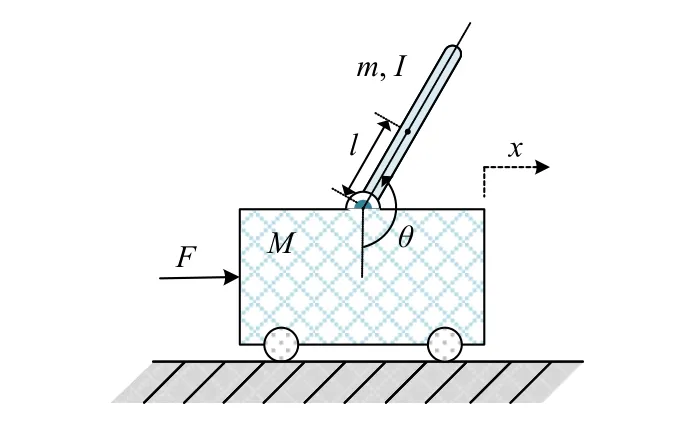
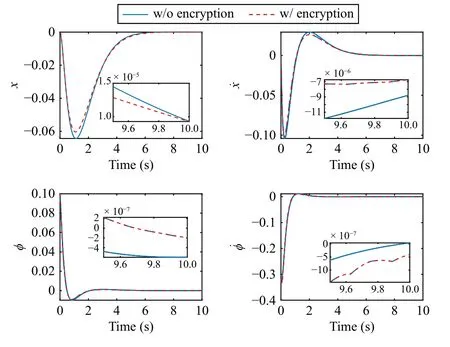
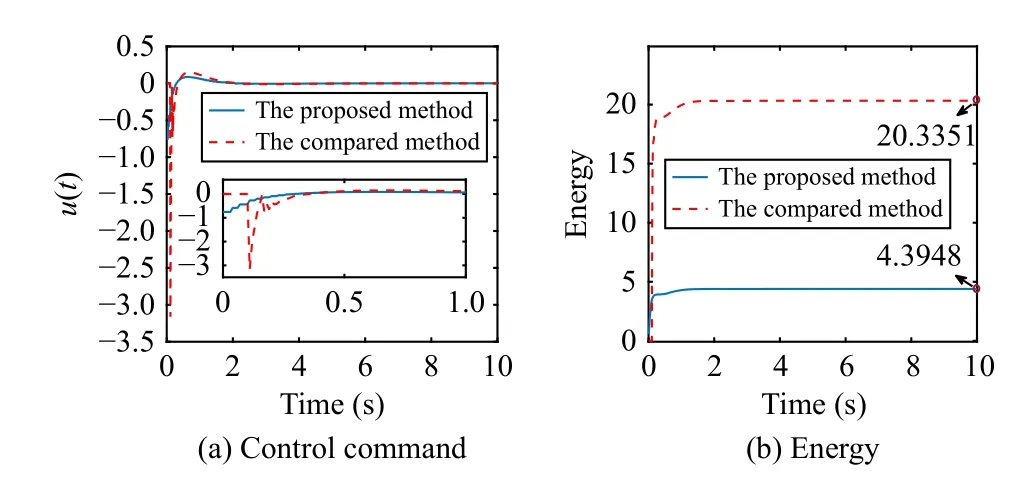
Let R, Z, and Z+be sets of the real numbers, integers, and non-negative integers, respectively.Denote Rnand Rn×mas sets of then-dimension column vector andn×mreal matrix.Let Z+n:={z∈Z:0 ≤z In this section, we first revisit the Paillier cryptosystem and the uniform quantizer.Then, the encrypted networked control problem is formulated. The Paillier encryption includes three steps, i.e., key generation (Gen), encryption (Enc), and decryption (Dec).The detailed operations are as follows [20]: 1)Gen a) Choose two large prime numberspandqrandomly such that gcd(pq,(p-1)(q-1)) = 1, where gcd(a,b) stands for the greatest common divisor of any positive integersaandb; b) Generate the public key (N,g), whereN=pqandg∈is a random integer; c) Generate the private key (λ,µ), whereλ=lcm(p-1,q-1), µ=λ-1modN, lcm(a,b) is the least common multiple of any positive integersaandb, and mod is the modulo operation. 2)Enc a) Select randomr∈Z∗N:={x∈Z+N|gcd(x,N)=1}; b) Given a plaintext messagem∈Z+N, construct its ciphertext asc=Enc(m)=gm·rNmodN2. Since the data related to the practical NCSs, such as the sensor measurements and control gain, are usually real numbers,they must be quantized before encryption.For any real numberx∈R , a uniform quantizerqu(x):R →Z is defined as [22] Similarly, the quantization error of vectorv(i.e.,v˜=v-∆qu(v) ) and the quantization error of matrixS(i.e.,S˜ =S-∆qu(S)) can be upper bounded as Consider the linear networked control system wheret∈Z+is the time index,x(t)∈Rnis the system state,u(t)∈Rmdenotes the control input,A∈Rn×nandB∈Rn×mare the constant matrices.If the matrix pair (A,B) is controllable,the system (6) can be stabilized by implementing the statefeedback control law whereK∈Rm×nis the control gain matrix.As illustrated in Fig.1, the control input signal (7) is computed by a networked controller according to the state measurements.A malicious adversary can directly obtain sensitive state measurements by eavesdropping the communication channels.Moreover, the controller may be implemented using an untrusted computing entity, e.g., a cloud-based controller.Since valuable information can be inferred from the state measurements or the control input signal, the security and privacy of the system may be compromised.Hence, this paper focuses on the secure control problem of NCSs, stated as Problem 1. Fig.1.The NCSs subject to possible eavesdropping attacks. Problem 1: Develop an encrypted control framework for the linear networked system (6), including a static quantization policy for the control gainKand a state-based dynamic quantization policy for the system statex(t), and an event-triggered policy to achieve the following objectives: 1) Ensuring the asymptotic stability of the closed-loop system; 2) Preserving the security of the data shared through the communication network; 3) Reducing data transmissions over the communication network between the plant and the controller. Lemma 2[23]: Consider the linear networked system (6)with the state-feedback control law (7).If the matrix pair(A,B)is controllable, for any given symmetric and positivedefinite matrixQ∈Rn×n, there existsP=PT∈Rn×n>0 satisfying Assumption 1: For the networked control system (6) with state-feedback control law (7), (A,B) is controllable. Remark 1: Given that the Paillier cryptosystem only operates positive integers, all data used for computing the networked control law necessitate integer conversions.Hence,the purpose of employing uniform quantizers in this paper is to map the real-valued system state and control gain into proper integer values.Although the uniform quantizer itself distorts the original signal, protecting data only through quantization seems impracticable as the variation trend of the original signal remains unchanged after quantization.Thus, the security enhancement of the NCS still relies on the usage of the Paillier cryptosystem. In this section, a novel encrypted networked control framework is proposed, as shown in Fig.2.First, we design the static and dynamic quantization policies to quantize the control gainKand the system statex(t), respectively.Remarkably, the main purpose of the quantization is to convert the real-valued control gain and system state into integers since only integers can be encrypted in the Paillier cryptosystem.Then, a state-based event-triggered strategy is developed for scheduling the transmission of the quantized system state before encryption.Based on this, an encrypted networked controller is constructed.Finally, the inter-event time interval under the proposed event-triggered policy is analyzed.The detailed design and analysis procedures are introduced below. Fig.2.The proposed encrypted networked control scheme, where (E (u+) is the encrypted control law computed by the networked controller, u + is the decrypted result of E (u+) , and u (t) is actual control command executed on the actuator. 1)Quantization for the Control Gain Matrix Based on the description in Section II,Kis the control gain matrix in (7) and satisfies (8).Letqu(K) be a uniform quantizer ofKwith the sensitivity ∆K>0.Then, the static quantization policy for the uniform quantizerqu(K) is designed such that ∆Ksatisfies wherePandQare positive-define matrices in (8). which directly implies In summary, as long as ∆Kis determined by (9), it is straightforward to infer from (13) that the linear networked system (6) is asymptotic stable. Additionally, based on Theorem 1, there exists symmetric positive-define matricesP¯ andQ¯ such that which is a discrete Lyapunov equation and will be used in the design of the quantization policy for the system state. 2)Quantization for the System State Letqu(x) denote a uniform quantizer of the system statexwith the sensitivity ∆x>0.Then, the state-dependent dynamic quantization policy is designed such that with Fig.3.Comparison of quantization errors. where inf(·) is the infimum operation, the initial triggering instant ist1=0, andF(t) is the triggering function given by with an adjustable factor where ε>0 is a position constant.Note that the proposed event-triggered strategy (22) is Zeno-free, thus it is executable.The detailed analysis of the inter-event time interval of (22) is provided in the later part of this section. The detailed implementation of the proposed encrypted control scheme is summarized in Algorithm 1, where Dp(·) is the Paillier-based decryption operation. Algorithm 1 The Implementation of the Proposed Encrypted Control Scheme With Static and Dynamic Quantizers and the Event-Triggered Policy p,q,g,rk,K,Q, ¯Q, ¯Qx Initialize: choose Ensure:1: /*Parameter computation*/2: Compute P according to (8)3: /*Static quantization*/∆K u(t)4: Select so that (9) holds qu(K) ¯K 5: Compute and¯P 6: Compute according to (14)7: /*Dynamic quantization*/8: Compute σ and select such that (15) holds qu(x)∆x 9: Obtain¯Px 10: Compute according to (21)11: /*Event trigger*/12: Compute β based on (24)t=tk+i,i=1,...13: for do F(t)14: Calculate using (23)F(t)≥0 15: if then 16: Determine by (22)tk=tk+1 tk+1 17:18:e(t)=0 19: Update 20: end if 21: end for 22: /*Encryption*/qu(K) rk qu(x(tk))23: Encrypt using a random positive integer qu(x(tk))24: Encrypt using Paillier encryption Erk(qu(K)) EP(qu(x(tk)))25: Transmit and to the controller node 26: /*Controller*/E(u+)27: Compute the encrypted controller as per (25)E(u+)28: Transmit to the plant node 30: Compute 29: /*Decryption*/u+ = -Dp(Drk(E(u+)))= -Drk(Erk(qu(K))qu(x(tk))) =-qu(K)qu(x(tk))31: /*Scaling*/u(t)=-¯K¯x(tk)32: Obtain and implement Theorem 3: Consider the linear networked system (6) and suppose that there is no saturation occurrence in the uniform quantizer.Implementing the encrypted control law (25) with the event-triggered strategy (22) following Algorithm 1, the control objectives stated in Problem 1 are achieved. Proof: Benefiting from the homomorphic property of Paillier encryption, we haveu(t)=∆K∆xu+.Thus, the actual control commandu(t) executed on the actuator is represented by Therefore, the linear networked system (6) now becomes Therefore, the closed-loop control system under the proposed encrypted control scheme is asymptotically stable.Moreover, under the event-triggered policy, the system state is encrypted and transmitted only when the specific triggering condition is fulfilled, which contributes to communication load reduction.Furthermore, the data security during network transmissions is clarified by Remark 2.■ Remark 2: According to Fig.2 and Algorithm 1, all data transmitted over the communication network, i.e., the system state, control gain, and control input signal, have been encrypted before transmission.Since the private key is exclusively known by the plant, no sensitive information, particularly the system state and controller signal, can be leaked even in the presence of network eavesdroppers and malicious adversities, which ensures the security and confidentiality of data shared through the communication channel. Remark 3: Considering the design process of the encrypted networked control scheme, we present the static, dynamic quantization policies, the event-triggered strategy, and the encrypted control law successively.Combining the proof of each theorem, it is easily observed that Theorem 2 is obtained based on the premise of a discrete Lyapunov equation (14)generated from Theorem 1.Similarly, the discrete Lyapunov equation (21) generated by Theorem 2 is used to construct the event-triggered strategy (22), which drives the encrypted control law (25).Hence, Theorem 1 is a prerequisite for Theorem 2,and Theorem 2 is a prerequisite for Theorem 3. In this section, the encrypted control of an inverted pendulum cart system shown in Fig.4 is considered as an example to validate the efficiency of the proposed event-driven encrypted control framework.The motion equation of the inverted pendulum cart system is described by [25] Fig.4.The schematic of an inverted pendulum cart system. Figs.5 and 6 show the state trajectories and the actual control commands for the encrypted control law (25) (denoted as“w/ encryption”) and unencrypted control law (7) (denoted as“w/o encryption”), respectively.These two figures confirm that the asymptotic stability and control performance of the encrypted control system are similar to those of the unencrypted control system.The triggering release instants and the inter-event triggering intervals under the proposed event-triggered strategy (22) are plotted in Fig.7, where the triggering number, minimum, and maximum triggering intervals, are 165, 2 and 15, respectively. Fig.5.State trajectories under the encrypted and unencrypted control systems. Fig.6.Control command under the encrypted and unencrypted control systems. Fig.7.The triggering instant and inter-event interval. Fig.8.Comparison of the energy consumption between the encrypted and unencrypted control systems. Fig.9.Comparison of the communication size between the encrypted and unencrypted control systems. Fig.8 depicts the energy consumption of the encrypted and unencrypted control systems.In Fig.9, we show the communication size for the unencrypted control system (denoted as“w/o encryption”), the proposed event-driven encrypted control system (denoted as “w/ encryption”), and the encrypted control system without an event-triggered policy (denoted as“w/ encryption w/o trigger”).The unencrypted control system only requires 4-byte to communicate each variable or parameter, while the Paillier encryption scheme requires 8-byte to communicate each variable.In this case, the sizes of data transmitted over the communication network under the proposed encrypted control law (25) and unencrypted control law(7) are 6616 bytes and 20 016 bytes, respectively.Without consideration of the event-triggered policy (“w/ encryption w/o trigger”), the system requires 40 016 bytes to transmit the encrypted data.Therefore, the total size of data transmitted over the communication network is significantly reduced under the proposed event-triggered encrypted control scheme.Moreover, combining Fig.8 with Fig.9, the proposed encrypted control scheme increases the energy consumption by nearly 3.34%, while reducing the communication size by 66.95%compared with those under the unencrypted control law, which indicates it is still resource-efficient. The encrypted system states and control law are depicted in Figs.10 and 11, respectively.As can be seen, there is no correlation exists between the original/actual data (Figs.5 and 6)and the encrypted data (Figs.10 and 11).Therefore, the sensitive state measurements and the control input signal transmitted over the communication network are well protected. Fig.10.The encrypted system states of the system. Fig.11.The encrypted control law of the system. It is worth noting that [20] addressed the same event-triggered encrypted control problem of NCSs as our work.Specifically, the Paillier cryptosystem, uniform quantizer, and eventtriggered control method were utilized to construct the encrypted controller.Hence, the encrypted control scheme in[20] is simulated as a comparative example, named “The compared method”.To ensure a fair comparison, the system parameters and control-related matrices remain unchanged with subsection A.However, in order to maintain the scaling factor Ω ∈(0,1) as specified in [20], the saturation value of the uniform quantizer for the system state is increased to 50 000.Due to space limitations, we have omitted the encrypted system states and control law. Fig.12 shows the state trajectories under these two encrypted control schemes.It is evident from Fig.12 that both schemes ensure the asymptotic stability of the system.However, the proposed method in this paper exhibits a better transient control performance, contributing to smoother control command and less energy consumption, as depicted in Fig.13.In Fig.14, the updating time instant and interval of the timevarying quantizer in [20] are plotted, with a total of 89 updates.It is important to note that the event-triggered condition in [20] heavily relies on a parameter Θ used in the timevarying quantizer, and the triggering error can not be reset to zero at every triggering instant.In our simulation setting, we have Θ ≈400.In this case, the event-triggered condition in[20] can be always satisfied.As a result, although the updating number of the time-varying quantizer is reduced, it results in a large number of triggering instances, which implies that the size of data transmitted over the communication work in[20] amounts to 40 016 bytes.Overall, in contrast to the encrypted control scheme in [20], the encrypted control scheme proposed in this paper reduces the energy consumption by 7 8.39% and reduces communication size by 8 3.47%. Fig.12.State trajectories under two encrypted control schemes. In this paper, a novel event-driven encrypted control framework of NCSs was proposed using semi-homomorphic encryption.By designing the quantization policies with the static and dynamic sensitivities, the bounded quantization error inherent in the traditional fixed-sensitivity uniform quantizer was tactfully compensated, contributing to the system state’s asymptotic convergence.Moreover, an event-triggered strategy was developed to reduce the communication consumption of NCSs and relieve ciphertext expansion.With the aid of static/dynamic quantization policies, event-triggered strategy, and Paillier encryption, the asymptotic stability and the data security of NCSs are ensured simultaneously.Finally,the validity of the proposed encrypted control framework was investigated through a numerical example of motion control of an inverted pendulum cart system.Future work will focus on the secure control problem of NCSs subject to more practical constraints, such as parameter uncertainties and exogenous disturbances. Fig.13.Comparisons of control command and energy under two encrypted control schemes. Fig.14.The updating instant and updating interval of time-varying quantizer in [20].II.PRELIMINARIES AND PROBLEM FORMULATION
A. Paillier Cryptosystem
3) Dec

B. Uniform Quantizer


C. Problem Formulation

III.MAIN RESULTS

A. Quantization Policy Design




B. Event-Triggered Strategy

C. Encrypted Control Law


D. Inter-Event Time Interval Analysis

IV.SIMULATION EXAMPLE



A. Effectiveness Verification




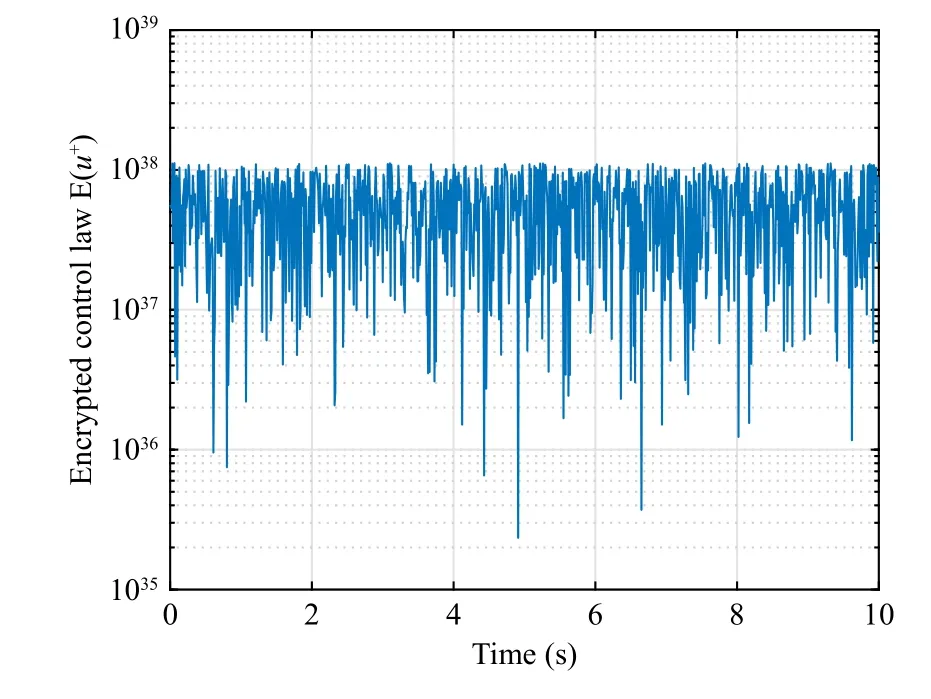
B. Comparison With the Existing Method
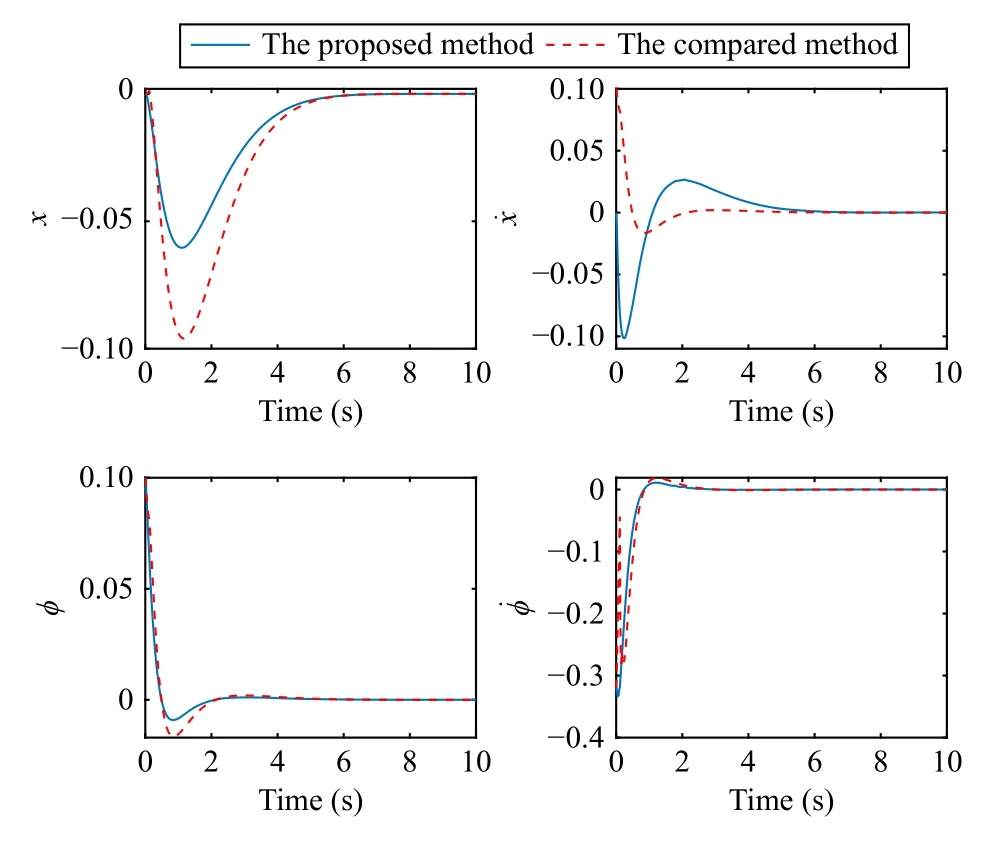
V.CONCLUSION

杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- When Does Sora Show:The Beginning of TAO to Imaginative Intelligence and Scenarios Engineering
- Goal-Oriented Control Systems (GOCS):From HOW to WHAT
- Digital CEOs in Digital Enterprises: Automating,Augmenting, and Parallel in Metaverse/CPSS/TAOs
- A Tutorial on Federated Learning from Theory to Practice: Foundations, Software Frameworks,Exemplary Use Cases, and Selected Trends
- Cybersecurity Landscape on Remote State Estimation: A Comprehensive Review
- Data-Based Filters for Non-Gaussian Dynamic Systems With Unknown Output Noise Covariance
