结构理解：思维从“形式”走向“实质”

顾刘兵

［摘 要］“用数对确定位置”是平面上位置确定的种子课，体现二维空间的结构特征和表征需求。教学以“打地鼠”游戏贯穿始终，按照数对生长的关键节点和学习节奏设置问题链，驱动学生经历确定位置的全过程，实现从技巧方法的“形式理解”走向对结构价值的“实质把握”，有效渗透一一对应和数形结合的思想，助力学生空间观念的有序生长和空间表达能力的提升。

［关键词］数对；确定位置；结构理解；思维实质

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2024）08-0014-04

“用数对确定位置”属于图形与几何领域，主要研究图形（点）的位置，初步建构“直角坐标系（限于第一象限）”模型，苏教版教材将它安排在四年级下册第八单元。在此之前，学生已经会用“方向+距离”的方式描述和记录一维空间中物体的相对位置。现在，研究视角从一维走向二维，既符合学生的认知规律，也遵循知识的螺旋建构原则。换个角度来看，二维空间点的位置确定可以解构为两个不同维度，每个维度仍然以“方向+距离”的方式描述和记录，整个学习过程应体现空间结构的有序生长。

需要指明的是，两个维度的有机组合不能忽视以下问题。第一是“方向确定”，解决“怎么看”，原点（观察点）是两个维度纵横交错的要点（起点），需要凸显；第二是“距离确定”，解决“怎么数”，以整数方式表征数的结果，需要强化；第三是“顺序确定”，解决“怎么说”，“先列后行”的数学规定与生活经验，需要对接；第四是“模型确定”，解决“怎么写”，简洁表达逗号和小括号的作用，需要阐释；第五是“价值确定”，解决“怎么用”，点、线、面的位置确定之间需要关联。明确了“学什么”和“学到什么程度”，接下来就要考虑“怎么学”。笔者准备以学生喜闻乐见的“打地鼠”游戏贯穿教学始终，按照知识生长的关键节点和节奏设置问题链，驱动学生在玩中学、在学中玩，最终实现确定位置从技巧方法的“形式理解”走向空间结构的“实质把握”。

一、玩中调用经验，明确结构特征

（一）横向玩

师：大家喜欢玩“打地鼠”游戏吗？

生（齐）：喜欢。

师（出示图1）：瞧，小地鼠钻出来了，它在什么位置？

生1：小地鼠在从左往右数的第4个洞。

师：还可以怎么数？

生2：小地鼠在从右往左数的第2个洞。

（二）纵向玩

师（出示图2）：瞧，小地鼠又钻出来了，它在什么位置？

生3：小地鼠在从上往下数的第4个洞。

师：还可以怎么数？

生4：小地鼠在从下往上数的第2个洞。

（三）理结构

师（同时出示图1和图2）：要想精准描述地鼠的位置，你觉得需要确定什么？（板书：确定位置）

生5：要确定从哪里往哪里看，还要确定它在第几个。

师：从哪里往哪里看，是在确定方向；第几个，是确定观察起点和终点之间的距离。用“方向+距离”来确定位置是个好办法。（板书：方向+距离）

师：为什么图中小地鼠的位置都有两种描述结果？

生6：观察的起点不同，数的距离就不一样。

师：会用联系的眼光看待方向和距离，给你点赞！现在我们知道，在横向或者竖向中只要有一个带方向的数，就能确定一个物体的位置。

【思考：一维空间结构认知是二维空间结构认知的先决条件和发展基础，必要的復习可以让学习更自然。首先，通过创设一维空间问题情境，驱动学生调用确定位置的经验，主动描述小地鼠的具体位置，“还可以怎么数”指向方向变化时对应的距离随之改变，渗透方向与距离之间的动态关联。其次，空间形式从横向变换为竖向，引导学生用两种角度描述位置，加强方向与距离的动态关联。最后，通过对四种描述结果的整体比较，提炼出“方向”和“距离”这两个确定位置的关键要素，明确一维空间中确定位置的结构特征，感受确定位置时观察起点的重要性，揭示方向和距离之间的动态关联，固化一维空间中位置确定的方法，为后续学习做好铺垫。】

二、玩中迁移经验，经历结构生长

（一）不具体，怎么办？

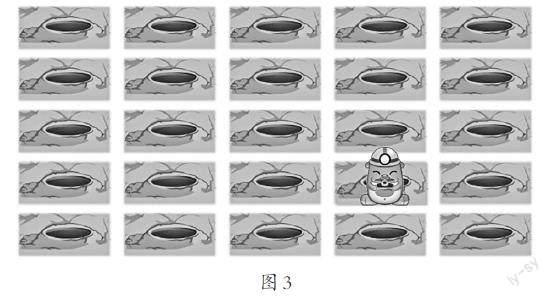
师（出示图3）：小地鼠可聪明了，扩大了鼠洞范围，有竖有横，纵横交错，现在只用一个带方向的数还能确定它的位置吗？如果不具体，又该怎么办？

师（组织学生描述小地鼠的位置，要求小组讨论并确定一种方法，写在板贴的横线上，然后有序地贴到黑板上的展示区）：请边指边数，分享你确定位置的过程。

生1：小地鼠在从左往右数的第4个洞，从上往下数的第4个洞。

生2：小地鼠在从左往右数的第4个洞，从下往上数的第2个洞。

生3：小地鼠在从右往左数的第2个洞，从上往下数的第4个洞。

生4：小地鼠在从右往左数的第2个洞，从下往上数的第2个洞。

师（手势比画）：先横向数，再竖向数，能确定小地鼠的位置。换个角度，还可以怎么数？

生5：先竖向数，再横向数。

师：角度不同，但是都用了几个带方向的数？

生（齐）：2个。

师：看来，要想具体描述平面上地鼠的位置，需要2个带方向的数。

【思考：要学生理解结构，教师就不能机械地单向传输，而是需要学习者亲历探究过程，充分调用和迁移已有认知，借助适宜的问题驱动思考，逐步完善、完成和完美。首先，创设纵横交错的二维空间情景，引导学生思辨“只用一个带方向的数”能否满足位置确定的需求，并以“不具体，怎么办？”的核心问题使学生经历尝试、碰撞和共鸣的全过程，学习的主动性成就了探究的有效性。其次，通过追问“换个角度，还可以怎么数？”，驱动学生从“先横向数，再竖向数”的习惯转换为“先竖向数，再横向数”，体现表征结果的丰富性。最后，引导学生聚焦描述内容的实质，归纳出平面上确定物体位置的结构特征和数量特点，初步理解二维空间位置确定的方法。】

（二）不统一，怎么办？

师：小地鼠位置不变，描述结果却不统一，怎么办？（出示活动要求，如图4）

师：哪一组来分享一下自学成果？

（教师组织学生围绕圈画的关键词逐一弄懂“列”和“行”的名称、方向和顺序。重点交流“第1列在哪里？怎么看？”和“第1行在哪里？怎么看？”）

师：列和行都是以谁为观察点，这样规定有什么好处？

（邀请学生站在讲台前分别观察其他学生的位置和小地鼠的位置，寻找确定位置和观察方向之间的对应联系）

生1：站在讲台上面向学生，从左往右数确定第几列，从前往后数确定第几行，转过身，面向图片中的小地鼠，确定其位置的方法相同。

师：按照这样的规则，小地鼠的位置在哪里？

生1：小地鼠的位置在第4列第2行。

【思考：二维空间的位置确定可以解构成纵、横两个维度。因此，用“两个带方向的数”确定物体位置，是由二维空间的特性决定，不以人的意志为转移。但是，多元表征同时带来了描述结果“不统一”的现实问题，这就需要人为干预和约定。自主学习是重要的学习方式之一，通过“约定解读”和“规则表征”的活动创设，驱动学生自读要求、自审题意、自想办法。“读懂”和“会用”是活动质量的评价标准，数学表征形式从丰富多元走向了规范统一，数学化学习的要求和水平有所提高。】

（三）不简洁，怎么办？

师：冬天到了，大雪覆盖地面，鼠洞变成一个个小圆点，就成了点子图。我们来玩个游戏，当小地鼠出现时，请用“第×列第×行”描述它的位置。

（课件演示小地鼠出现的速度由慢到快，直至学生来不及记录）

师：这样记录位置让人感觉怎么样？

生（齐）：太麻烦。

师：想要玩好游戏，该怎么办？

（教师组织学生以“第4列第2行”为例，自创简洁记录位置的方法。教师巡视并选取典型的学生作品，鼓励学生板演在黑板上的展示区中。）

师：大家一起来评判，这样表示简洁吗？

（教师组织学生对“4列2行”“4  2”“4、2”“4，2”等表示方式进行评价，重点交流简洁方式及干扰因素。）

师：仔细观察，这些表示方式有什么相同之处？

生1：都有4和2，而且出现的顺序不变。

生2：它们都表示“第4列第2行”。

师：形式简洁了，内容没有变，也不能变。你想知道数学家遇到这个问题是如何解决的吗？

生（齐）：想。

师：伸小手，一起来。先写4，再写2，中间用逗号隔开，两边添上小括号表示这是一个整体，缺一不可。（4，2）这样的数叫作“数对”，读作“数对四二”，也可以直接读“四二”。这就是我们今天要研究的内容——用数对确定位置。

【思考：数学模型的建构形式有简洁的需求。通过游戏的生动介入，引领学生浸润自主创造、集体研讨和简洁介绍的全过程，使得空洞的说教变得可感知、可操作和可评价。需要注意的是，简洁表达并没有改变空间的结构实质，只是对原有数学表征进行二次加工，体现了“从数学到数学”的纵向数学化理解。换句话说，位置确定从多元表征阶段就已经体现了数对的内涵，后续的规则、简洁表示只是数学表征形式的外部需求，千万不能本末倒置，否则不利于学生空间观念的有序建构。】

三、玩中运用经验，理解结构实质

（一）顺向玩

课件出示：我想打           鼠，它的位置用数对表示是                       。

師（出示图5）：问题解决了，想不想继续打地鼠？

生（齐）：想。

（教师组织学生玩游戏）

（二）逆向玩

课件出示数对：（5，3）（4，1）（1，3）（3，1）。

师：刚才大家能够根据小地鼠的位置说数对。反过来，如果给数对，你能找到它的位置吗？游戏继续，小地鼠就位。

（教师组织学生玩游戏）

师：（1，3）和（3，1）为什么数字相同，位置不同？

生1：因为（1，3）表示“第1列第3行”，（3，1）表示“第3列第1行”，所以它们表示的位置不同。

生2：数字虽然相同，但是顺序不同，对应的位置也就不同。

师：看来，数对和位置是一一对应的。

（三）明结构

课件出示数对：（2，1）（2，2）（2，3）（2，4）。

（教师组织学生玩游戏）

师：表示同一列小地鼠位置的数对有什么特点？

生1：数对的第一个数都相同。

师：如果只显示（2，         ），能确定什么，不能确定什么？

生2：能确定列数，不能确定行数。

课件出示数对：（1，3）（2，3）（3，3）（4，3）。

（教师组织学生玩游戏）

师：表示同一行小地鼠位置的数对有什么特点？

生3：数对的第二个数都相同。

师：如果只显示（       ，3），能确定什么，不能确定什么？

生4：能确定行数，不能确定列数。

师：看来，知道一个数，可以确定列数或行数，同时知道两个数，才能确定物体的具体位置。

【思考：结构理解离不开巩固运用，但如何操作和实施，则需要精心设计、指向明确和梯度安排。首先，“顺向玩”侧重物体位置转化为数学表达，主要演绎位置实质到形式表征的抽象过程，渗透行列规则和列行顺序，“弄懂”“会说”是评价标准。其次，“逆向玩”侧重数学表达转化为物体位置，主要演绎形式表征到位置实质的具象过程，尤其是对（1，3）和（3，1）的深度对比，学生依据规则理解数对内涵，建立数对与平面上点的位置的联系，形成一一对应的数学思想。最后，“明结构”侧重单个数对与多个数对的联系，主要归纳“同一列数对”和“同一行数对”的结构特征，使学生在“变与不变”中动态理解数对内部“两个带方向的数”的实质。】

四、玩中内化经验，感悟结构价值

（一）建模型

师（动态出示图6）：瞧！点子图变成了方格图。小地鼠可调皮了，从A点跳到B点，你能用数对表示B点的位置吗？

生1：B点的位置用数对（6，3）表示。

师：只要把方格图再扩大些，就能确定它的位置。如果跳到C点，要想表示它的位置，怎么办？

生2：可以把方格画得再密一些。这样，C点就有对应的列和行，也就能够用数对表示了。

（二）链历史

师：看来，只要网足够大、足够密，平面上任意一点的位置都可以用数对来表示，这是伟大的数学家笛卡尔发现的。让我们一起“穿越”吧！

（简要介绍笛卡尔由蜘蛛织网现象联想和创造用数对确定位置的过程）

（三）悟价值

师（出示情境图，图略）：小地鼠们正在玩“排排队”的游戏，你能用数对表示这三只小地鼠的位置吗？

生1：A点是（2，2），B点是（4，5），C点是（4，2）。

师：自己课后在这个图上找一个D点，要求和原来3个点连成一个你认识的图形，并结合图形特征，与同学交流数对的特点。

【思考：价值感悟是结构理解的组成部分，看似比较抽象，其实非常重要。首先，“建模型”侧重位置确定涵盖的对象，主要分两种情况加以引导。一种是以原有列行的单位标准继续扩大确定范围，仍然用整列整行来描述位置；另一种是需要确定的位置坐落在非整列非整行，那就需要细化列行的单位标准。对于用小数描述位置的情况，不要求学生现在就能掌握，但是该情况的出现有利于学生对数对内涵的理解前后一致，思维从特殊走向一般。其次，“链历史”侧重讲述数对产生的故事，丰富了学生对知识的情感体验，增强了学生对用数对确定位置的认同感，使学生的数学思维从冰冷走向火热。最后，“悟价值”侧重确定对象之间的逻辑架构，从平面上“點”的唯一表达推理出“线”的唯一确定，进而理解“面”的唯一架构，使得图形特征与数对特点对比融合，学生思维从解构走向重构。有了这样的价值体验，学生的数学视野变得开阔，数学思考变得有力，数学表达变得清晰。】

【本文系江苏省教育科学“十三五”规划重点课题“基于问题链驱动的小学生数学化学习的研究”阶段性成果（课题批准文号：C-b/2020/02/26）和江苏省中小学教学研究第十五期立项课题“指向‘三会素养的小学数学游戏化学习设计研究”阶段性成果（课题批准文号：2023JY15-L190）。】

（责编 金 铃）