超声波风速传感器风场误差的数值模拟

顾仁勇 ，蒋 泽 ，王 璐 ，郝叶军

（1.中煤科工集团常州研究院有限公司，江苏 常州 213015；2.天地（常州）自动化股份有限公司，江苏 常州 213015）

煤矿通风系统为煤矿井下输送新鲜空气，是煤矿安全生产的基础保障。井下环境恶劣，风速传感器容易受温度、潮湿、粉尘等条件的影响[1-2]。现有的差压式、超声波涡街式、热敏式风速传感器启动风速均大于0.3 m/s，难以满足《煤矿安全规程》中最低风速0.15 m/s 的测量要求[3-5]。煤矿智能通风建设亟需低风速高精度测风装置，以实现矿井的全覆盖精准测风。

随着科学技术的发展，基于时差法的高精度超声波风速传感器逐渐发展成熟，并在气象测风领域广泛应用[6-7]。超声波风速传感器具有测量范围宽、精度高、稳定性好等优点，但由于其结构特点，迎风侧的换能器后会形成特定的尾迹区，使得风速的测量值出现偏差，即阴影效应。换能器的阴影效应是造成传感器测量误差的主要原因之一[8-9]。

超声波风速传感器按换能器的布置方式分为对射式和反射式。对射式结构以芬兰VAISALA 公司的产品为代表，2 组换能器呈十字交叉式正交布置；反射式结构以英国GILL 公司的产品为代表，相较于对射式放置方式，换能器的发射面依倾角对称布置，利用反射板加长了超声波的传播路径。不同结构传感器的风速测量受风场误差的影响也不尽相同。

针对换能器所产生的测量误差和阴影效应补偿，国内外研究学者已通过实验和数值模拟等手段开展了大量研究[10-13]，但是针对传感器不同结构布局对风场影响的研究较少。因此，利用计算流体动力学方法围绕对射和反射式2 种结构类型，分析了换能器不同布置方式对测风风场的影响，并对单向风速下的风场误差进行修正，为矿用超声波风速传感器设计提供参考。

1 超声波风速传感器测量原理

超声波风速传感器根据时差法原理测量风速，超声波时差法原理示意如图1。

图1 超声波时差法原理示意Fig.1 Schematic diagram of the principle of ultrasonic time difference method

收发一体的超声波换能器探头的位置固定，以固定频率发射超声波脉冲串。在顺风和逆风时，风速会对超声波传播速度分别产生叠加或减少的效果，通过测量超声波顺风和逆风的传播时间来计算风速和风向[14]。超声波传播路径上风速计算公式如下：

式中：vpath为超声波传播路径上风速，m/s；L为超声波传播路径长度，m；ts为超声波顺风的传播时间，s；tn为超声波逆风的传播时间，s。

对射式超声波风速传感器的结构及测量原理如图2。

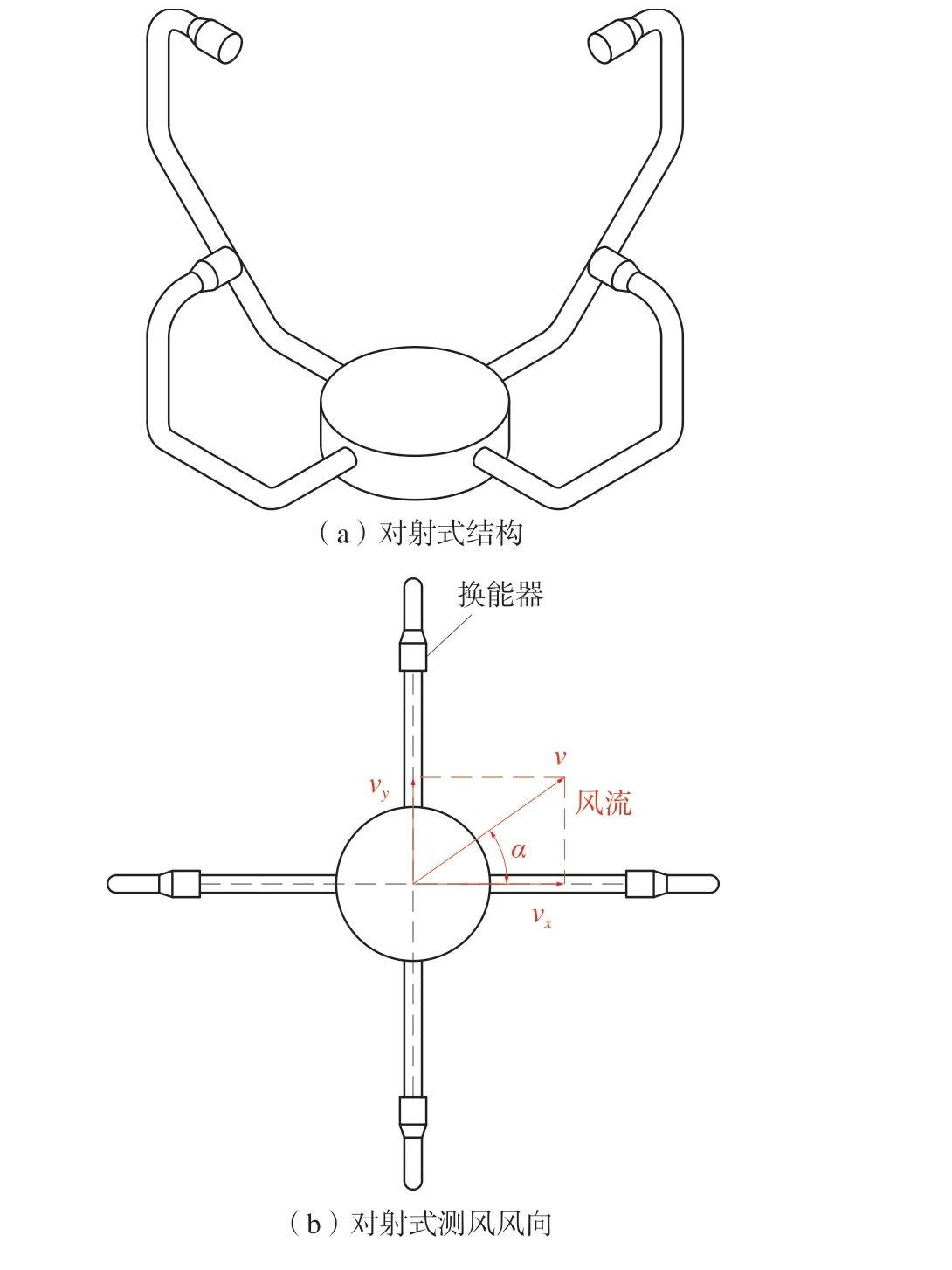
图2 对射式结构及测风原理Fig.2 Schematic diagram of opposite-type structure and wind measurement principle

对射式超声波风速传感器实际测量时，通过式（1）分别计算2 条超声波传播路径上的风速，再将风速叠加获得来流风速和风向，风速和风向的计算公式如下：

式中：v为来流风速，m/s；vx为x轴方向的来流风速分量，m/s；vy为y轴方向的来流风速分量，m/s；α为风向角，（°）。

反射式结构及测风原理如图3。

图3 反射式结构及测风原理Fig.3 Schematic diagram of reflection-type structure and wind measurement principle

2 建模与仿真

2.1 计算模型与网格划分

计算模型参照实际工程应用的超声波风速传感器：①设定对射式结构的2 对换能器十字交叉正交布置，换能器直径为12 mm，换能器距离为194 mm；②设定反射式结构的壳体外径为140 mm，过风通道截面高度为41 mm，超声波发射角θ为45°。

反射式结构不同换能器安装方案如图4。

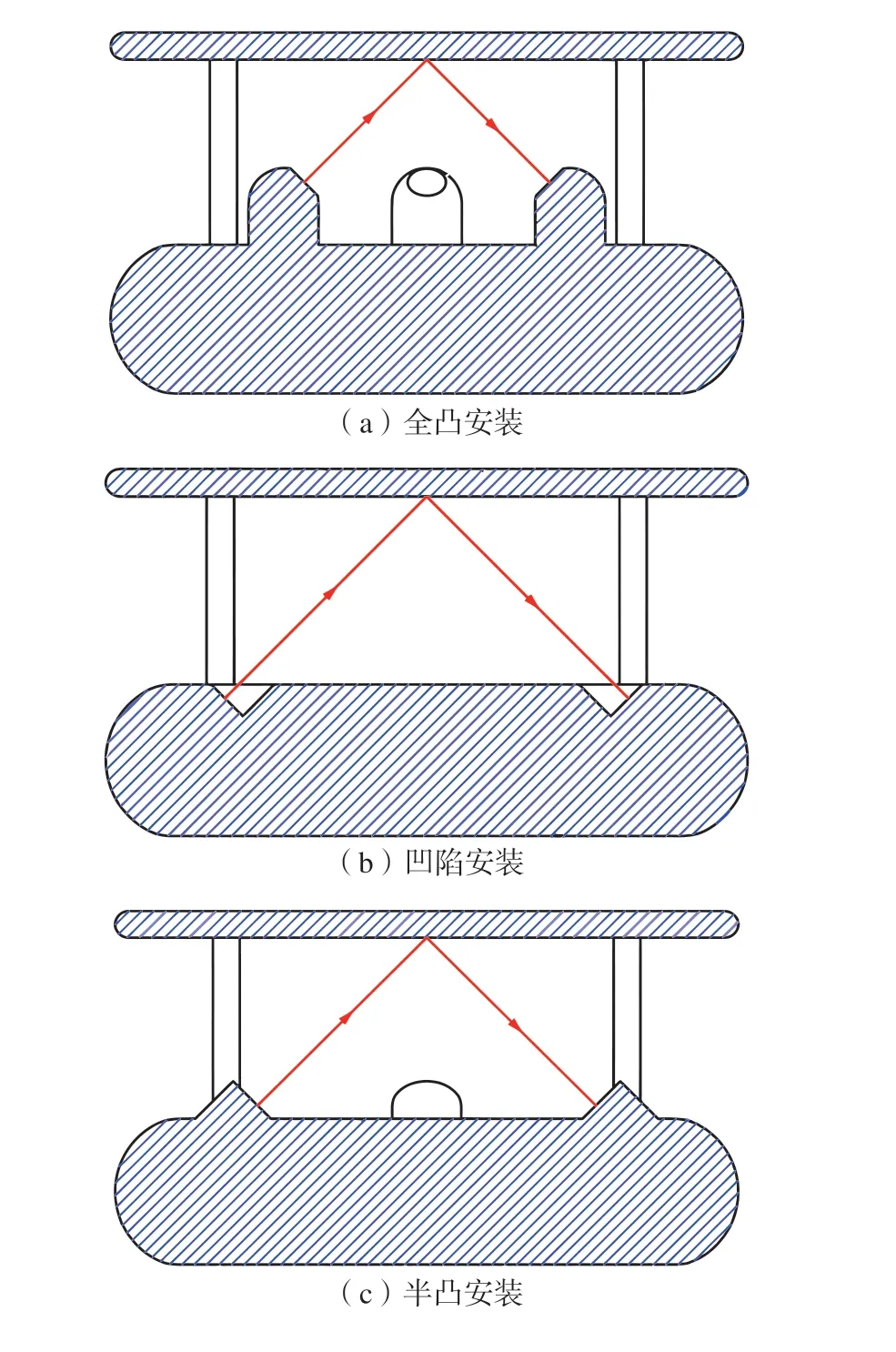
图4 反射式结构不同换能器安装方案Fig.4 Schematic diagram of different transducers with reflection-type structure

反射式超声波风速传感器需利用反射板加长传播路径，传播路径会与来流风速呈一定角度。通过式（1）计算获得的路径风速为风流的投影风速，需换算为x和y方向的风速分量后，再代入式（2）和式（3）获得风速和风向。投影风速换算公式如下：

式中：vpath,x/y为x或y轴方向的路径风速，m/s；θ为超声波发射角，（°）。

根据换能器前端面与传感器壳体的位置关系，设定3 种类型的换能器布局。①全凸安装：換能器的前端端面完全暴露于流场；②凹陷安装：换能器完全缩入传感器壁面；③半凸安装：安装位置介于凹陷安装与凸出安装之间。3 种安装方式换能器测风路径距离分别为78.8、124.4、107.4 mm。

参照矩形风硐尺寸，在传感器外构建了0.8 m×0.8 m×4 m 的长方体流场域，以满足计算精度要求。采用四面体非结构网格进行划分，考虑到风场在换能器附近会产生复杂的流动分离，在换能器和壳体壁面设置10 层边界层网格，并对测风路径上的网格进行局部加密。进口设定为速度进口，出口设定为压力出口，其余边界为无滑移壁面。流体为不可压缩理想气体，湍流模型选用RNGk-ε模型。

在0°风向角，10 m/s 来流风速下，对换能器全凸安装方式进行网格无关性验证（图略），当网格数达到300 万后，测风路径上的平均风速保持不变，因此选定300 万网格规模对多套模型进行网格划分。

矿用传感器通常固定于巷道顶部，考虑到煤矿巷道风向的单向性，仅对风速值误差进行仿真分析。由于所研究模型均为轴对称结构，对比风向角0°和45°，即可分析出传感器测风受换能器阴影效应影响的最大及最小误差。《煤矿安全规程》规定：掘进中岩巷和其他通风人行巷道的最小允许风速为0.15 m/s，无提升设备的风井和风硐最大允许风速为15 m/s。根据雷诺数计算，风速由0.15 m/s 增加至15 m/s 的流动涵盖了层流、过渡流和湍流的多种流态。因此，计算分析了不同换能器布置方式在0°、45°风向角，0.15～15 m/s 风速下的流场，以获得因风场误差导致的测量误差数据。

2.2 数据处理方法

换能器测风路径上，由于阴影效应的影响，导致超声波传播速度的不均匀变化。在处理流场数据时，为真实模拟超声波在风场内传播的情况，不能简单通过提取声道上平均速度的方法来代替声道上的测量风速。为获得超声波脉冲渡越时间，需逐个计算路径上每个节点内的超声波声传播时间并进行积分累加，进而计算得出声道测量风速。

流场数据处理时，采用无穷小法对超声波传播路径进行等距分隔，将每个分割点作为检测点，每个间隔的距离为ΔLn，相邻2 点在声波路径方向的投影风速分量为vn-1和vn，则ΔLn小段的平均风速为（vn-1+vn）/2，在超声波无风下传播速度上叠加该小段的平均风速，然后就可计算出每小段间隔所需的传播时间Δtn，累加得到超声波脉冲渡越时间。获得ts和tn后，代入式（1）得出路径平均风速，进而换算得出来流测量风速。顺风、逆风时具体的传播时间的计算公式如下：

式中：ts、tn分别为顺风和逆风下的超声波传播时间，s；Δtns、Δtnn分别为顺风和逆风下每小段间距的传播时间，s；ΔLn为第n小段的间距，m；c为超声波无风下传播速度，m/s；vn为第n分割点的投影速度分量，m/s。

3 仿真结果

3.1 对射式结构仿真结果

对射式结构在不同风向角下速度云图（来流风速15 m/s）如图5。

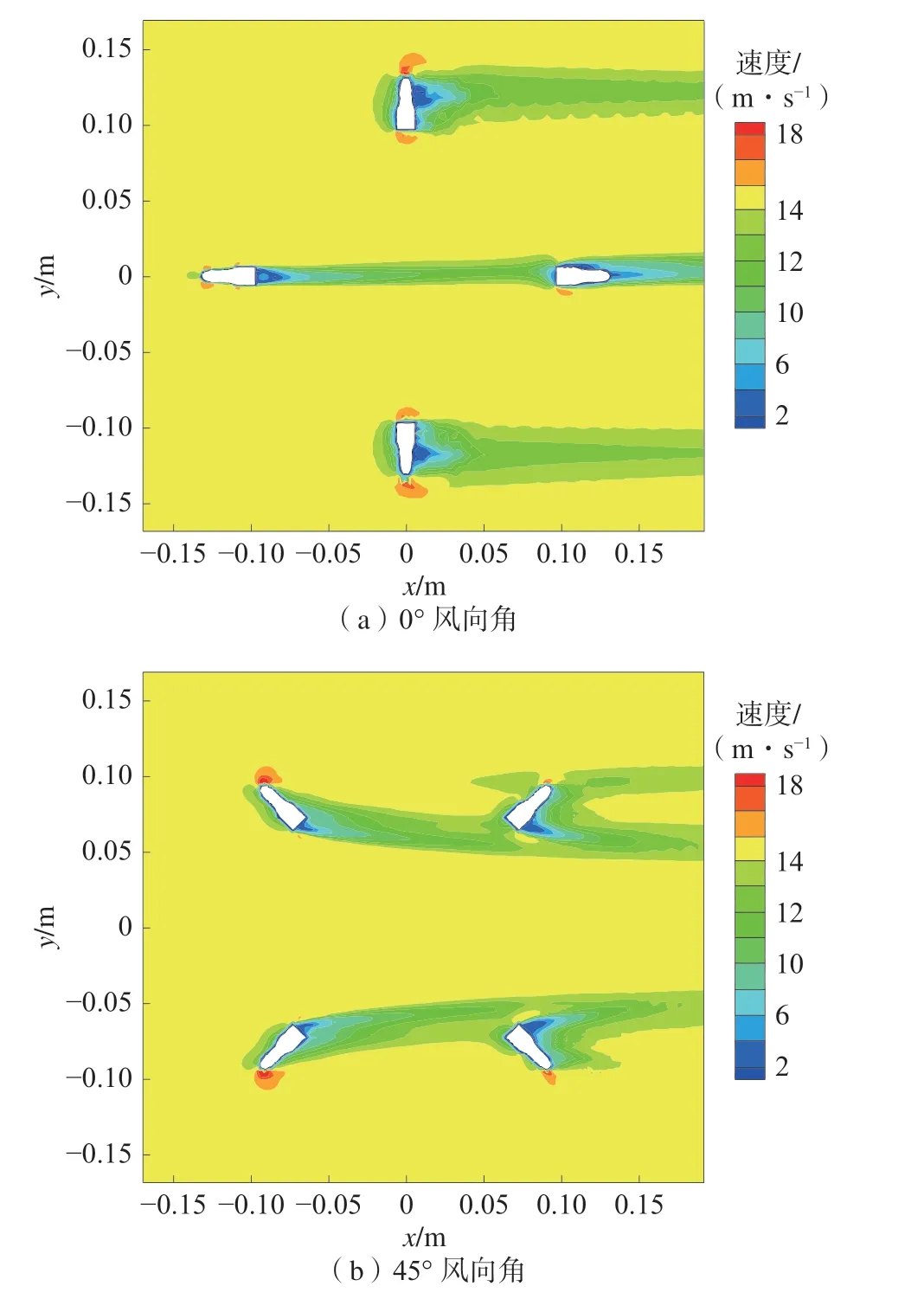
图5 对射式结构在不同风向角下速度云图Fig.5 Velocity distribution of opposite-type structure under different wind directions

由图5（a）可知，在0°风向角下，测量风速只由处于来流方向的路径平均风速决定，该条测风路径均处于上游换能器的风场阴影范围内，且在上游换能器的尾端会形成分离回流区。由图5（b）可知，在45°风向角下，测量风速由2 条路径平均风速叠加求得，测风路径上绝大部分区域不受换能器尾流影响，上游换能器尾端存在小范围分离回流区，上游换能器尾流有向中心靠拢趋势，而下游换能器头部区域刚好位于上游换能器尾流范围内。

为便于分析，对测风路径的速度分布进行归一化处理：将测风路径上速度分量除以来流风速在测风路径上的理论投影速度。对射式结构测风路径的速度分布如图6。

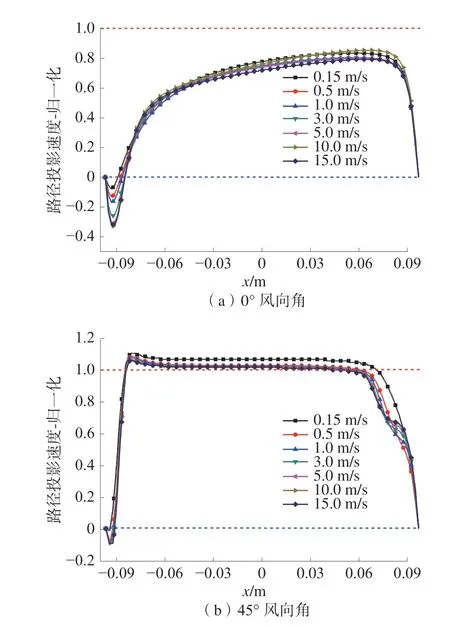
图6 对射式结构测风路径的速度分布Fig.6 Velocity distribution of wind measurement path of opposite-type structure

由图6（a）可知，在0°风向角下，整条测风路径均受尾流干扰；上游换能器尾端出现负速度，测风路径上的流速沿着流动方向逐渐增大，但整体流速均小于理论来流风速；随着来流速度增大，回流范围和回流负速度大小也相应增大。

由图6（b）可知，在45°风向角下，风场因受换能器挤压，流动面积减少，中心流动区域流动加速，且略大于理论来流风速；下游换能器头部区域受上游尾流影响导致速度较低；因测风路径上的流场受扰动较少，不同流速下的速度分布一致性也较好。

按照前文提供的风速计算处理方法，0°和45°风向角下的测风平均流速与来流风速的相对误差分别为-39.4% 和-9.6%。因此，采用对射式结构测风时，需重点考虑风向角对测风误差的影响，并确保传感器角度安装到位。

3.2 反射式结构仿真结果

风向角为0°时，测量风速只由处于来流方向的测风路径平均风速决定。反射式结构0°风向角下速度云图（来流风速15 m/s）如图7，反射式结构在0°风向角下测风路径的速度分布（来流风速15 m/s）如图8。

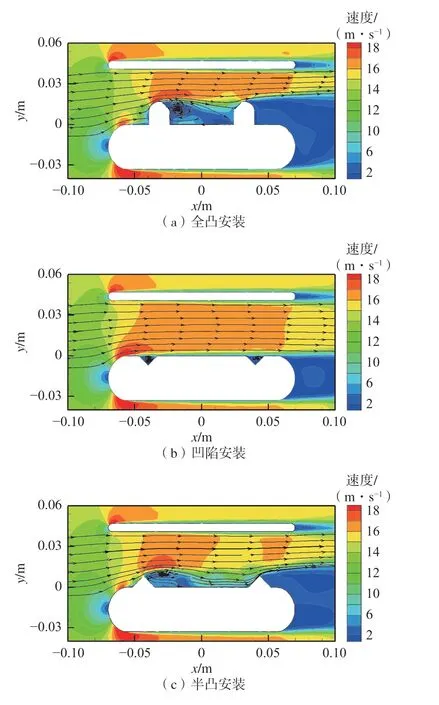
图7 反射式结构0°风向角下速度云图Fig.7 Velocity distribution of reflection-type structure at 0° wind direction angle

图8 反射式结构0°风向角下测风路径的速度分布Fig.8 Velocity distribution of wind measuring path of reflection-type structure at 0° wind direction angle

由图7（a）可知：换能器全凸安装时，上游换能器附近产生较大回流旋涡，但尾流对下游换能器影响较小；因为换能器倾入过风通道的尺寸最大，对流场的影响也最显著，风流受流通截面渐缩影响，流体明显加速。由图7（b）可知：换能器凹陷安装时，因换能器内嵌入传感器壳体内部，对流场的扰动最小，流速分布均匀，但上下游换能器的凹陷位置内存在回流旋涡。由图7（c）可知：换能器半凸安装时，上游换能器后存在明显附壁回流旋涡；下游换能器刚好处于上游换能器的湍流尾流中；流场扰动介于全凸和隐藏安装之间，但回流旋涡和换能器尾流对测风路径的影响却最大。

由图8 可以看出：3 种安装方式的主流流速均大于来流风速，中间区域因受反射面的壁面边界层影响流速先下降再回升；全凸安装因流动阻塞最大导致流体加速最大；半凸安装的测风发射路径和反射路径的差异性较大，在发射路径上存在因旋涡导致的负速度区间，在反射路径上又受上游尾流影响导致壁面边界层增大；凹陷安装由于回流旋涡区尺寸远小于前两者，且传播粒径较长，测风发射路径和反射路径的速度分布一致性较好。

风向角为45°时，测量风速由2 条正交路径平均风速叠加求得。反射式结构45°风向角下速度云图（来流风速15 m/s）如图9，反射式结构45°风向角下测风路径的速度分布（来流风速15 m/s）如图10。

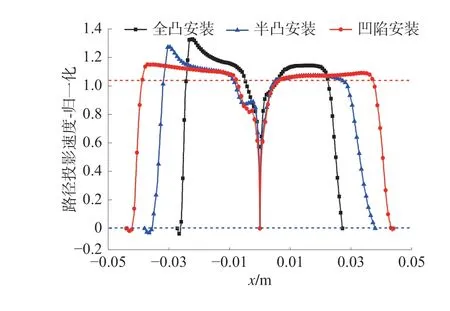
图10 反射式结构45°风向角下测风路径的速度分布Fig.10 Velocity distribution of wind measuring path of reflection-type structure at 45° wind direction angle

由图9 可知：3 种安装方式均受前端支柱的扰流影响；换能器全凸安装时，相比0°风向，换能器发射面已基本脱离换能器的尾流阴影，测风路径受尾流影响较小，但测风通道内流体加速最明显；换能器凹陷安装时，凹陷区域存在回流旋涡，传感器内部流场与0°风向时基本一致；换能器半凸安装时，换能器受换能器尾流、挤压加速和回流旋涡的影响介于全凸和隐藏安装之间。

由图10 可知：3 种安装方式的测风路径中部区域均受支柱绕流和反射面边界层的叠加影响；相比0°风向角，凸起安装的挤压加速效应增强；半凸安装受到尾流旋涡的影响减弱；凸起安装和半凸安装下的发射路径与反射路径的速度差异性增大。

综合对比0°和45°风向角，可以看出反射式结构中不同换能器安装方式对测风误差的影响因素区别较大。全凸安装的内部流场复杂，隐藏安装受扰动最小，半凸安装介于两者之间。

3.3 风速误差分析与修正

根据风场模拟结果，汇总的不同结构的测量风速与来流风速关系曲线（图略），不同结构在单一风向角下的测量风速与来流风速具有很好的线性相关性，相关系数均接近于1。不同结构的测量风速拟合曲线方程对比见表1。

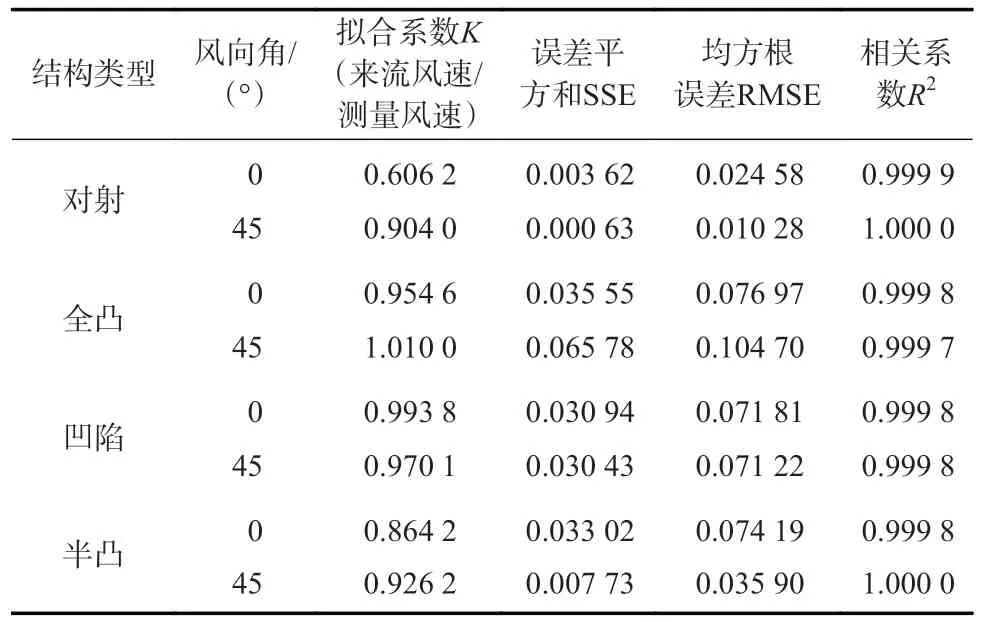
表1 不同结构的测量风速拟合曲线方程对比Table 1 Comparison of measured wind speed fitting curve equations of different structures

分析数据可以看出：对射式结构相比反射式结构对风向角更敏感，测量误差受风向角的影响更大，最大偏差可达约39.4%。在45°风向角下，对射式结构在不同流速下的流场一致性强，具有优于其他结构的拟合线性度。在巷道下使用时，对射式结构需保证传感器的安装角度，以确保测量数据的准确度。

而针对反射式结构，传感器内部风场较为复杂，不同换能器安装方式对测量的影响如下：

1）换能器全凸安装时，测风路径受换能器阻塞加速效应和尾流回流旋涡的双重影响；在0°风向角下，回流旋涡占主导，测量风速小于来流风速；在45°风向角下，阻塞加速效应占主导，测量风速又大于来流风速。内部流动复杂，导致线性度不如其余两者。

2）换能器凹陷安装时，过风通道内流场稳定，测量误差的影响因素包括流道加速、支柱绕流、壁面边界层和回流区旋涡，且回流区旋涡对低速流动的影响更为显著；不同风向角下的测量风速仅略低于来流风速，风速测量误差受风向角的影响较小。

3）换能器半凸安装时，测量风速在3 种反射式结构中最小；0°风向角下，测量误差影响因素与全凸安装一致，且测风路径受影响大于全凸；在45°风向角下，其受回流漩涡影响较弱，且其传播路径长度是全凸安装的1.36 倍，线性度优于全凸安装。

考虑到煤矿巷道风向的单一性，因此利用拟合系数K对单一风向角下的测风风速进行修正，不同结构测量风速修正后误差对比如图11。

图11 不同结构测量风速修正后误差对比Fig.11 Comparison of wind speed correction errors for different structures

由图11 可以看出：不同结构修正后相对误差均随流速增加而降低；对射式结构在45°风向角下的修正后相对误差最小，且优于反射式；反射式结构中，半凸安装在修正后相对误差最小，其原因在于换能器半凸安装时，换能器前端面的凸起结构可以确保不同流速下的流体在换能器附近稳定分离，流场的一致性较好。

4 结 语

利用数值模拟的方法研究了不同结构对超声波测风传感器风速测量误差的影响。

1）对射式结构的测量风速受风向角的影响大于反射式。对射式结构在45°风向角下经修正后的相对误差最小，且优于反射式。

2）反射式结构中，换能器凹陷安装对测量风速的影响最小，凸起安装其次，半凸安装影响最大。换能器凹陷安装的测量风速受风向角的影响最小，凸起安装和半凸安装影响相当。这3 种安装方式中，半凸安装在45°风向角下经修正后的测量误差最小。

3）选择合适的风速传感器结构，可以显著提升测量准确度。