半参数双重Tweedie复合泊松回归模型的贝叶斯分析
2024-04-13段星德伍震寰张钟妮张文专
段星德,伍震寰,张钟妮,张文专
(贵州财经大学数学与统计学院,贵州 贵阳 550025)
1.引言
在对健康保险行业进行研究时,人们常常分析卫生保健利用费用数据.而部分被保人在保险期间没有到医院进行医学治疗,因此这部分个体没有产生卫生保健利用费用.上述的卫生保健费用数据就是典型的半连续数据,即由零和正的连续数据所构成.近年来,对卫生保健利用费用数据进行统计建模,已取得了大量的研究成果.首先,Mihaylova等[1]综述了分析卫生保健资源及费用数据的各种统计方法,这些数据具有偏态、零过多、多峰、重右尾等特点;Smith等[2]利用边际两部分模型分析半连续卫生保健服务数据;Neelon等[3-4]综述了在卫生保健服务领域中零调整计数数据和半连续数据的建模方法及其应用;Merlo等[5]利用两部分分位数回归模型来分析半连续卫生保健费用纵向数据.上述文献中使用的两部分模型分别对零数据和连续数据进行建模,这样的分割处理给半连续数据整体属性的解释带来困难.其次,Kurz[6]利用Tweedie回归模型对半连续卫生保健费用数据进行建模,并与Tobit模型、泊松回归模型及两部分模型进行比较分析.
众所周知,Tweedie复合泊松分布是分析半连续数据的一个重要工具并且具有可解释半连续数据整体属性的优势,因此对Tweedie复合泊松回归模型的研究引起众多统计工作者的青睐.一方面,Smyth和Jørgensen[7]以及Andersen和Bonat[8]分别研究了双重Tweedie复合泊松回归模型(即对Tweedie复合泊松分布的均值和散度参数联合建模)统计推断问题并用这类模型分析半连续保险数据;Halder等[9]在双重Tweedie复合泊松回归模型引入空间效应并用它分析半连续保险费率制定数据.另一方面,在贝叶斯框架下,利用Markov Chain Monte Carlo(简称MCMC)技术对各类Tweedie复合泊松回归模型进行统计推断.比如: Peters等[10]利用Dunn和Smyth[11]给出的的数值方法去逼近Tweedie复合泊松分布的密度函数,并给出这类模型的贝叶斯分析;ZHANG[12],Swallow等[13]以及YE等[14]研究了Tweedie复合泊松随机效应模型的贝叶斯估计问题;段星德等[15]研究了Tweedie复合泊松回归模型的贝叶斯数据删除影响问题.在本文中,基于上述研究工作提出一类半参数双重Tweedie复合泊松回归模型,进一步对这类模型进行贝叶斯估计,最后利用这类模型分析卫生保健费用数据以及影响因素.
2.统计模型
本节将首先介绍Tweedie复合泊松分布以及逼近它的密度函数的数值方法,其次引入它们所对应的双重广义线性模型: 带有异质结构的Tweedie复合泊松回归模型.
Ⅰ Tweedie复合泊松分布
指数分布族是一类常见的分布族,在某些条件下Tweedie复合泊松分布是它的特殊情形.指数分布族的概率函数具有如下的一般形式:
其中,a(·)和k(·)的形式是已知的;θ常被称作自然参数,ϕ常被称作离散参数且ϕ>0.另外,指数分布族的均值和方差分别为:µ=E(Y)=k′(θ),var(Y)=ϕk′′(θ),其中k′(θ)和k′′(θ)表示k(θ)关于未知参数θ的一阶导数和二阶导数;特别地,函数k′′(θ)称为方差函数.进一步,如果方差和均值有如下关系var(Y)=ϕµp,其中参数p是取值范围为(1,2)的幂指标参数,则有k′′(θ)=µp,θ=µ1-p/(1-p)和k(θ)=µ2-p/(2-p).因此,(2.1)式可以表示为[16]:
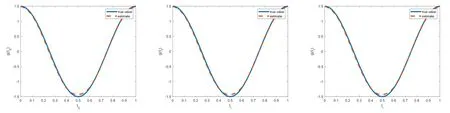
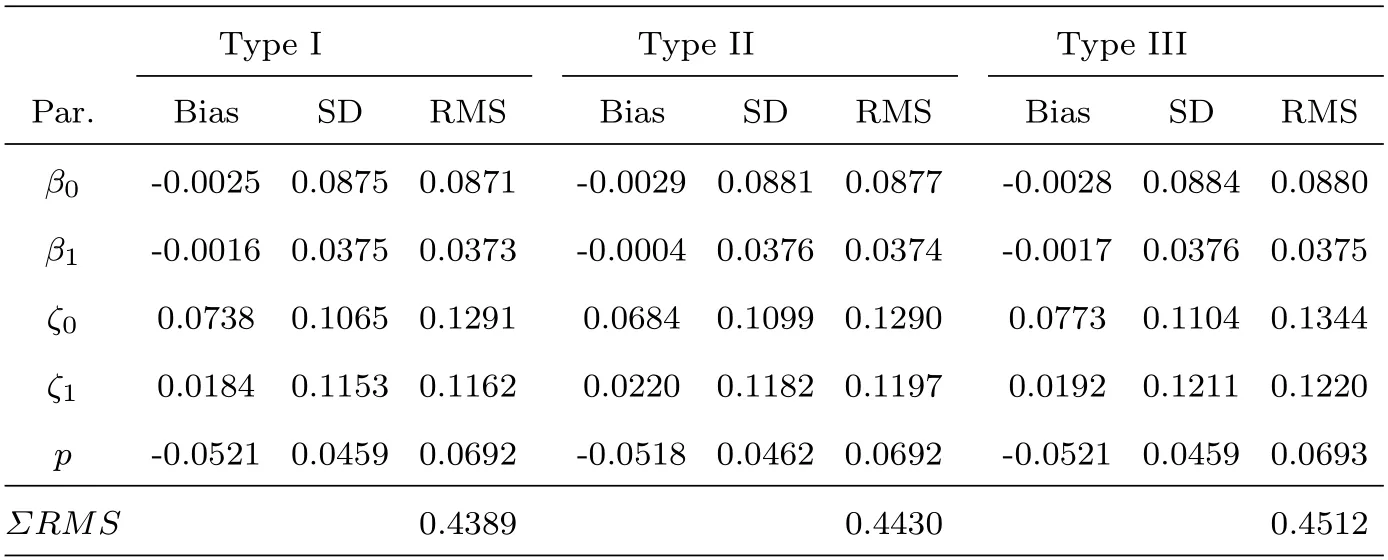
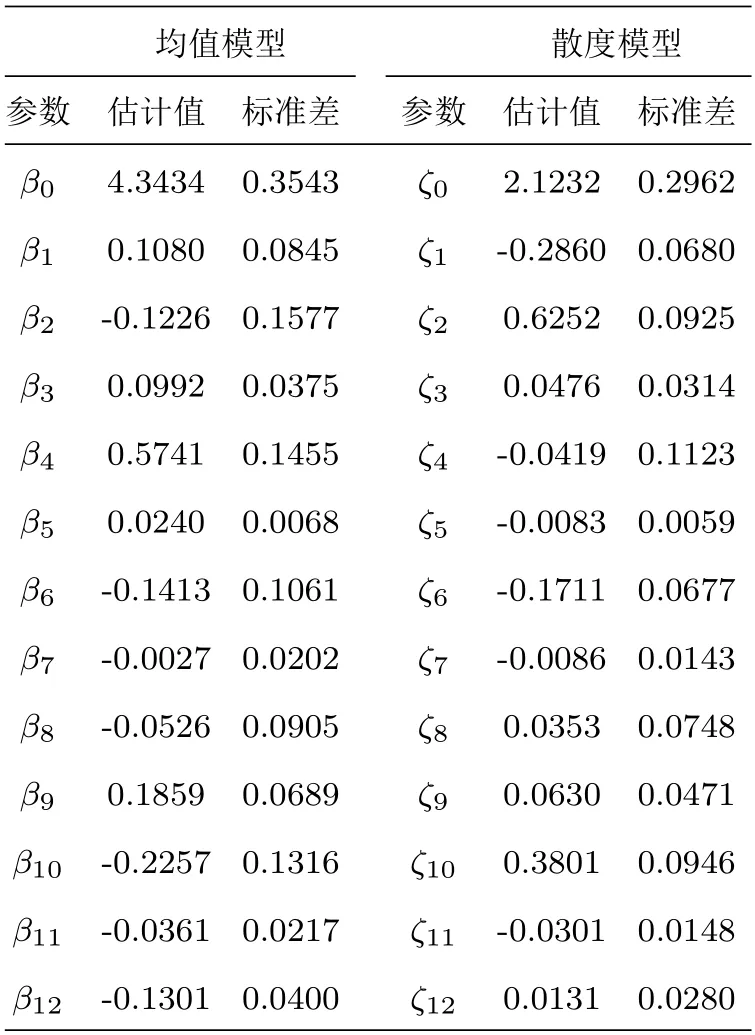
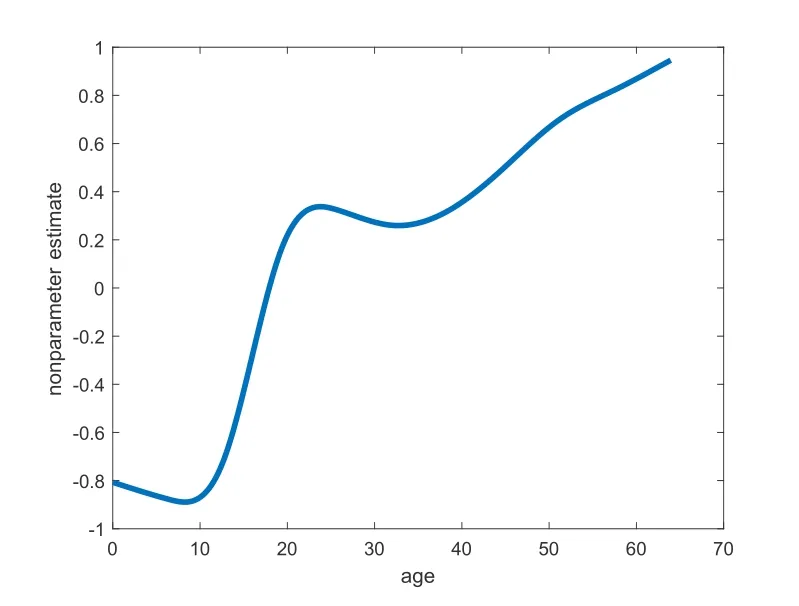
如果一个随机变量Y的概率密度函数具有(2.2)的形式且1 其中V(y)=ypI(y>0)+(y+v0)pI(y=0),这里v0是一个给定的较小的正数[9,17]. Ⅱ 半参数双重Tweedie复合泊松回归模型 在本文中考虑以下半参数双重Tweedie复合泊松回归模型,即对Tweedie复合泊松分布的均值参数和散度参数进行联合建模: 其中,Y=(Y1,Y2,···,Ym)T是m维响应变量且相互独立,xi=(xi1,xi2,···,xik)T表示均值模型中的协变量,zi=(zi1,zi2,···,ziq)T表示散度模型中的协变量.β=(β1,β2,···,βk)T,ζ=(ζ1,ζ2,···,ζq)T分别是k×1和q×1维未知待估参数向量,且k Ⅰ 先验分布与后验分布 其中µβ,Σβ,µζ,Σζ,aτ,bτ,aδ,bδ为已知的超参数,IG表示逆Gamma分布,Γ(a,b) 表示服从参数为a和b的Gamma分布.此外,本文在抽样过程中使用的条件分布、Gibbs抽样、MH算法如附录所示. Ⅱ 贝叶斯估计 为了得到平稳的随机序列,我们舍弃序列的前D个值,并保留来自联合后验分布p(θ|Y,X,Z,T)的随机样本{θ(n) :n=D+1,···,N},则有 Ⅰ 模拟研究 在模拟研究中,假设从如下模型结构中产生半连续响应数据{yi,i=1,2,···,m},即: 其中样本量m=200,协变量xi ∼N(0,1),zi ∼N(0,1),ti∼U(0,1).令参数和非参数真实值为β=(β0,β1)T=(0.5,1.5)T,ζ=(ζ0,ζ1)T=(-1,0.4)T,p=1.6,g(ti)=1.5×cos(2πti). 在贝叶斯框架下进行的模拟研究中,我们通常研究下面三种不同先验信息对贝叶斯估计的影响,即: 类型Ⅰ(良好的先验信息) 设超参数µβ的取值为β的真值,即µβ=β=(0.5,1.5)T,协方差阵Σβ=0.25I2,I2表示2阶单位阵;µζ=ζ=(-1,0.4)T,Σζ=0.25I2;aτ=1,bτ=0.005,aδ=0.5,bδ=0.5. 类型Ⅱ(不准确的先验信息) 设µβ=1.5×β=1.5×(0.5,1.5)T,协方差阵Σβ=0.75I2,I2表示2阶单位阵;µζ=1.5×ζ=1.5×(-1,0.4)T,Σζ=0.75I2;其它超参数的取值和类型Ⅰ一致. 类型Ⅲ(无先验信息) 设µβ=(0,0)T,协方差阵Σβ=100I2,I2表示2阶单位阵;µζ=(0,0)T,Σζ=100I2;其它超参数的取值和类型Ⅰ一致. 基于上述三种类型的先验信息,我们分别做100次实验的模拟研究,且每次实验都迭代10000次,为了避免最初产生的非平稳样本序列对后验推断的影响,我们舍弃前面产生的5000次迭代值,利用后面的5000 次迭代值来进行贝叶斯估计.另外,在实施MH算法时,我们选择方差调节参数=4,=0.7,=2,=0.6使得在抽样过程中所有参数的平均接收率在区间[0.26,0.35]上.表1给出了所有参数的Bayes估计、标准差和RMS(表示参数的Bayes估计与真值的偏差的平方的平均值的算术平方根).从表1中发现: 在三类不同先验信息下,所有参数的贝叶斯估计与真值的偏差都很小,说明我们模拟研究中所得到的贝叶斯估计都具有较高的精度且对先验信息不敏感;另外,参数的标准差和RMS 值也比较接近.我们在图1中列出类型Ⅰ、类型Ⅱ和类型Ⅲ先验下非参数g(t)的估计值与真实值的拟合图形,从图1中发现,非参数部分关于真实函数的拟合是比较好的,说明我们所使用的贝叶斯P-样条方法是有效的. 图1 类型I (左图),类型II (中图),类型III(右图)时非参数函数g(t)拟合图 表1 随机模拟研究中未知参数的Bayes估计 Ⅱ 实证分析 研究的数据来源于兰德健康保险实验(RAND HIE),该实验是对美国医疗成本、卫生保健利用率及相关结果的一个综合研究.[6]为了设计可靠的实验和得到精准的数据,该项研究跟踪了随机分配到不同计划的人群并记录了他们的医疗费用及个人信息.这里,我们选择了第五年观察期的1713个个体作为样本,并用ID标识不同个体.数据集中,卫生保健费用包括如下5种: 门诊费用(‘outpdol’)、药物费用(‘drugdol’)、供应费用(‘suppdol’)、心理治疗费用(‘mentdol’)和住院费用(‘indol’),我们把每个个体的5种卫生保健费用之和作为响应变量,并记为yi.另外,把个体信息: 性别(‘female’:1=女性,0=男性)、种族(‘black’:1=户主是黑人,0=户主不是黑人)、家庭收入对数(‘linc’)、身体缺陷数(‘physlm’)、慢性病数(‘disea’)、家庭规模对数(‘lfam’)、户主受教育年限(‘educdec’)和表示自评健康状况良好的虚拟变量(‘hlthg’)、保险特定变量包括对数共同保险率加1(‘logc’)、个人免赔额计划(‘idp’)的虚拟值、参与激励支付(‘lpi’)的对数和最大支出函数(‘fmde’)作为协变量,并把每个个体对应的12个协变量表示为xi1,xi2,xi3,xi4,xi5,xi6,xi7,xi8,xi9,xi10,xi11,xi12,把年龄(‘age’)作为非参数函数里的时间变量进行考虑并记为ti.在建模过程中,假定zij=xij,j=1,2,···,12,则用如下的模型拟合上述数据集: 同样,利用上述提出的MH算法和Gibbs抽样从联合后验分布中产生随机序列,在10000次迭代值中剔除前5000次,把后5000次迭代值作为后验样本值进行贝叶斯估计,计算结果见表2. 表2 实例分析中参数的估计值和标准差 由表2中的均值模型可以看出,对卫生保健费用支出有显著影响的协变量有家庭收入对数、身体缺陷数、慢性病数、保险特定变量、最大支出函数,而且前四个协变量对应的回归系数的符号都为正,这与定性分析的结果是一致的.另一方面,从散度模型中可以看出,性别、种族、家庭规模对数、个人免赔额计划的虚拟值、参与激励支付的对数这些协变量都是显著的;因此我们对散度参数进行建模也是合理的.非参数光滑函数g(age)的贝叶斯估计结果见图2,由函数g(age)的P样条估计可见其具有明显的非线性效应. 图2 实证分析中非参数函数g(age)的贝叶斯估计 本文利用Gibbs抽样技术和Metropolis-Hastings(MH)算法的混合算法去研究半参数双重Tweedie复合泊松回归模型的联合贝叶斯估计问题.最后利用提出的方法分析兰德健康保险实验中的半连续卫生保健费用数据. 6.1 条件分布和Gibbs抽样 为了利用Gibbs抽样技术从后验分布进行抽样,我们首先基于(3.1)-(3.2)式推导出如下步骤的满条件分布: 步1 给定Y,X,Z,T,p,ζ,ξ下β的满条件分布为 步2 给定Y,X,Z,T,β,p,ξ下ζ的条件分布为 步3 给定Y,X,Z,T,ζ,β,ξ下p的条件分布为 步4 给定Y,X,Z,T,β,ζ,,δ下ξ的条件分布为 步5 给定ξ,δ下的条件分布为 6.2 MH算法 为了利用MH算法对(6.1)-(6.4)给出的满条件分布进行抽样,步骤如下: 第二,从均匀分布U(0,1)中产生随机数u,若u ≤ a(β(n),β∗),令β(n+1)=β∗,否则令β(n+1)=β(n),其中接受概率为: 同样,参数ζ,p,ξ可用上述方法产生随机样本.3.贝叶斯分析
4.数值例子
5.结论
6.附录
