489 米超高层建筑抗倒塌分析案例研究

顾栋炼，吴小宾，张庆林，彭志桢，刘宜丰，田 源，陆新征

(1.北京科技大学土木与资源工程学院，城镇化与城市安全研究院，北京 100083；2.中国建筑西南设计研究院有限公司，成都 610042；3.中海发展成都超塔公司，成都 610000；4.清华大学土木工程系，土木工程安全与耐久教育部重点试验室，北京 100084)

随着我国快速的经济增长和城镇化进程，超高层建筑在我国得到了广泛的应用。以世界高层建筑与都市人居学会[1]对超高层建筑的定义为准，结构高度超过300 m 的建筑为超高层建筑，中国目前已成为世界上超高层建筑数量最多的国家。

由于超高层建筑自身的复杂性，其安全设计面临着巨大的挑战。超高层建筑往往是城市的地标建筑，周围地段繁华，人口和财富高度集中。若超高层建筑发生倒塌，不仅给建筑本身带来巨大损失，同时还可能产生坠物等次生灾害，进而危及周边环境，对城市的经济和社会发展造成沉重打击。因此，超高层建筑的抗倒塌设计是其安全设计中的重要一环，保障超高层建筑的抗倒塌性能对于保护人民生命财产安全具有重要意义。

自然灾害和人为灾害都可能引发超高层建筑的倒塌风险。一方面，我国的超高层建筑面临着严峻的地震灾害威胁，据统计我国75%以上的超高层建筑均位于抗震设防烈度达7 度和8 度的中高烈度区[2]，极端地震下超高层建筑的结构倒塌风险不容忽视；另一方面，爆炸、撞击等人为灾害也可能导致超高层建筑的关键竖向构件失效，从而导致结构发生连续倒塌[3]。因此，针对超高层建筑的地震倒塌风险和爆炸、撞击引起的连续倒塌风险，设计中均需要科学评估。但是，由于倒塌分析技术难度较大，因此在实际工程中应用案例还很有限。

ZHANG 和HE[4]基于多条带分析方法和一次二阶矩方法，对一座具有典型巨型框架-核心筒-外围支撑体系的118 层超高层建筑进行了地震倒塌风险评估，结果表明建模不确定性对超高层结构的倒塌承载力影响较小而地震动随机性的影响较为显著。杜东宁等[5]基于颗粒流理论建立了一80 层核心筒-框架结构的建筑模型，进而模拟了火灾下该建筑的倒塌形态；崔铁军和马云东[6]用同样的建模方法研究了不同位置爆破时该栋建筑的倒塌形态。但上述研究所采用的有限元模型均无法完全模拟出结构倒塌过程中构件级别的强非线性行为特征，因而在指导设计或改造时提供的参考较为有限。

LU 等[7-9]通过纤维梁、分层壳和生死单元技术，提出了可以模拟超高层建筑倒塌全过程的有限元模型建模方法，并模拟了中国最高建筑“上海中心”、北京最高建筑“北京中信大厦”等系列超高层建筑的抗地震倒塌性能。然而，既有关于超高层建筑抗倒塌能力的研究，主要集中于外围框架连续的常规框架-核心筒结构。随着建筑业的不断发展，部分超高层建筑为了满足部分楼层的无遮挡视野需求，外围框架的纵向传力体系可能在这部分楼层断开，形成独特的不连续的外围框架体系。对于这类非常规的框架-核心筒结构，其抗倒塌风险的研究尚且较少，业内也缺乏相关的设计经验。

为此，本文在LU 等[7-9]提出的超高层建筑倒塌模拟模型的基础上，以一栋489 m 的非常规超高层建筑为例，对其在地震、爆炸和拆除构件等情景下抗倒塌能力进行了模拟与评估，具体而言：首先采用增量动力分析(Incremental dynamic analysis,IDA)方法[10]进行了该建筑的抗地震倒塌能力评估；然后，基于该建筑所处地理位置和实际情况，开展了两种可能爆炸情景下的抗倒塌性能评估；最后，采用拆除构件法[11]分析了该超高层建筑在关键竖向构件拆除后剩余结构的抗连续倒塌性能。

1 研究对象和分析模型

1.1 研究对象简介

本文研究的超高层建筑位于抗震设防7 度区，抗震设防类别为乙类，设计地震分组为第三组，场地类别为Ⅱ类。地上共95 层，建筑高度488.9 m，结构高度463.5 m，高宽比为7.0。

该超高层建筑采用“核心筒-巨型框架-外伸臂”作为主要抗侧力体系，主体结构主要由核心筒、巨型框架(包括巨柱和环带桁架)、外伸臂桁架、次级钢框架构成。在89 层以上的观光层，由于建筑体型收进，外周框架采用钢框架代替巨型框架，形成“钢框架-核心筒”体系；在90 层以上不再采用核心筒，仅保留钢框架体系。

结构核心筒底部尺寸约为34.2 m×35.4 m，在41 层～43 层、71 层～77 层、78 层～82 层发生三次缩进，最终核心筒尺寸减小为27.2 m×27.1 m。核心筒翼墙底部的厚度约为1400 mm，往上逐渐减薄至450 mm；腹墙在底部的厚度约为700 mm，往上逐渐减薄至450 mm。在底部加强区的墙体采用钢板剪力墙形式。整体结构的抗侧力体系如图1 所示。

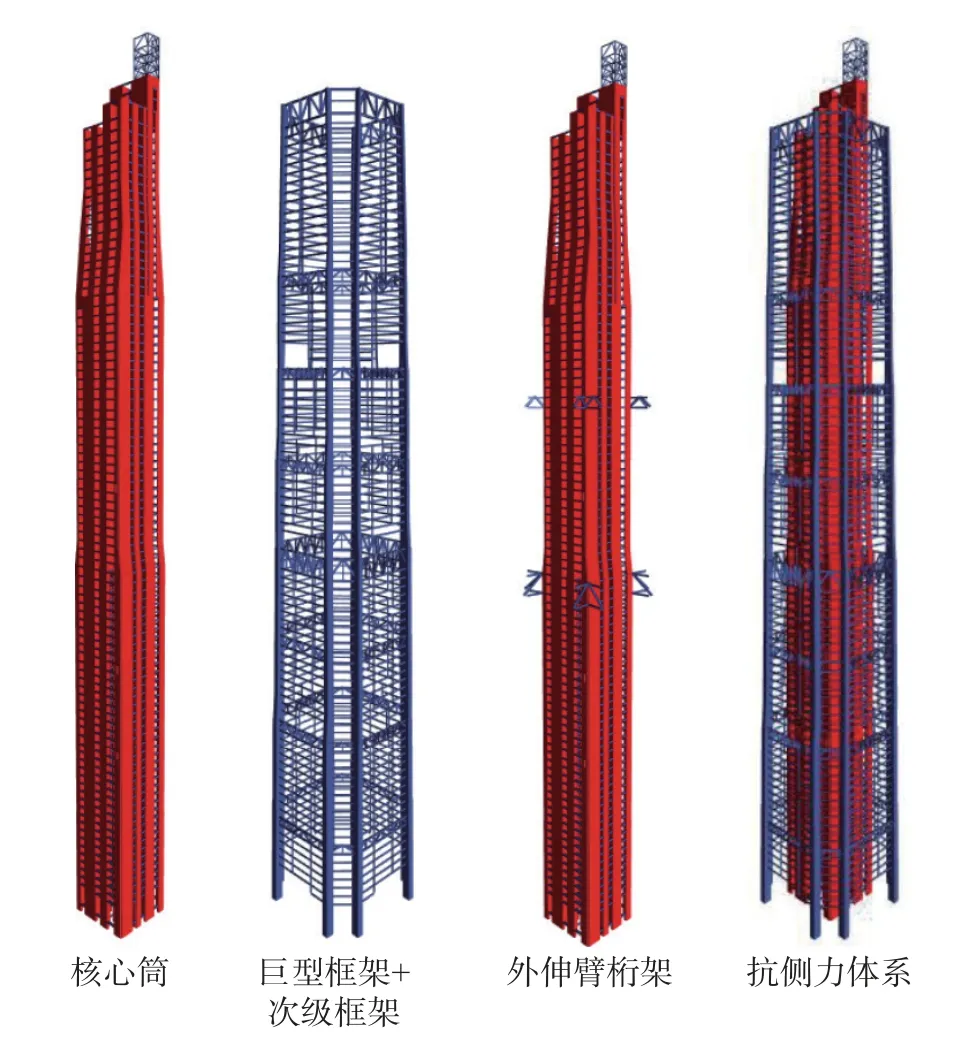
图1 超高层结构的抗侧力体系Fig.1 Lateral force resistance system of the prototype supertall structure

此外，如图2 所示，与常规超高层建筑不同的是，此超高层结构为了满足建筑设计需要，外围框架在4 个分区(即图2 中Z1、Z3、Z5 和Z6)采用“半吊半坐”设计，使得部分重力柱在正常情况下为吊杆，可能对整体结构的抗倒塌能力造成影响。

图2 外围框架重力柱布置与传力路径Fig.2 Layout and force transmission path of gravity columns in the peripheral frame

1.2 分析模型

为满足该超高层结构倒塌模拟的复杂结构建模、强非线性分析和高性能计算需求，本文以非线性计算性能良好的大型通用有限元程序MSC.MARC为平台，建立了该结构的弹塑性有限元模型。

建模的基本方法如下，此建模方法的合理性已在诸多研究中得到验证[7-9,12-13]。

1) 核心筒剪力墙及连梁由常规钢筋混凝土和边缘构件共同组成，采用分层壳模拟核心筒剪力墙及连梁中的常规钢筋混凝土部分。而边缘构件的配筋，按照实际配筋面积，采用嵌入墙体的Truss单元(与分层壳单元共节点)进行模拟；

2) 采用清华大学开发的纤维梁单元和THUFIBER程序[12]模拟核心筒内钢筋混凝土梁；

3) 钢骨混凝土巨柱由钢骨、混凝土和钢筋组成，其中：混凝土和钢筋部分采用纤维梁单元进行模拟，钢骨采用薄壁截面梁单元进行模拟，模拟巨柱钢骨的薄壁截面梁单元与模拟巨柱钢筋混凝土的纤维梁单元通过共节点设置实现共同工作；

4) 采用薄壁截面梁单元模拟次级钢框架的钢梁和钢柱、环带桁架和外伸臂桁架；

5) 钢材和混凝土的材料参数均依据相应规范选用对应的平均值；

6) 采用1 倍恒载加0.5 倍活载作为重力荷载代表值，恒载和活载数值依据《建筑结构荷载规范》(GB 50009-2012)[14]并考虑工程实际进行选择，楼面活载采用折算入楼板材料密度的方法进行施加。

7) 建筑倒塌过程中伴随着部分构件的失效，本文采用生死单元技术来“杀死”退出工作的构件单元，实现倒塌过程中构件失效模拟，并采用基于材料层次的应变作为基本的失效准则，不同类型材料的失效准则基于文献[2]进行设置，典型材料的失效准则如表1 所示。

表1 典型材料的失效准则Table 1 Failure criteria for typical materials

对于无约束的混凝土，其本构模型一般采用Kent-Park 模型，可以《混凝土结构设计规范》(GB 50010-2010) 附录C 中的表C.2.4 中混凝土的极限压应变εcu(即应力-应变曲线下降段应力等于0.5 倍峰值应力时的混凝土压应变)作为其无约束混凝土单元的失效准则。对于约束混凝土，可分为两大类：钢筋混凝土柱核心区的约束混凝土和钢骨混凝土巨柱核心区的混凝土。对于钢筋混凝土柱核心区的混凝土，分析时采用Mander 约束混凝土模型[16]考虑其约束效应，故相应的采用0.5 倍峰值应力对应的压应变(即第一根箍筋断裂时所对应的状态)作为其单元的失效准则；对于钢骨混凝土核心区的约束混凝土，分析时采用HAN 等[17]提出的钢管混凝土本构来考虑约束效应，相应的选用0.1 倍峰值应力所对应的压应变作为单元的失效准则。对于普通的钢筋，《建筑抗震设计规范》(GB 50011-2010)[18]第3.9.2 款第2 条规定“钢筋在最大拉力下的总伸长率实测值不应小于9%”，故本报告分析时偏于安全地采用了规范中规定的总伸长率下限9%作为钢筋断裂的失效准则；对于钢结构中的型钢，《建筑抗震设计规范》(GB 50011-2010)[18]第3.9.2 款第3 条规定了钢结构的钢材“应有明显的屈服平台，且伸长率不应小于20%”，因此，分析时采用20%的应变作为钢材单元的失效准则。

以环带和伸臂桁架为间隔，本文研究的超高层结构可以划分为10 个节段，分别命名为Zone 1～Zone 10。基于以上建模方法，最终得到该超高层结构的三维有限元模型如图3 所示。

采用MSC.MARC 进行基本动力特性分析，结构前3 阶阵型的模态分别为x方向平动、y方向平动和整体扭转，周期分别为8.96 s、8.71 s 和6.12 s。此外，进一步建立了该超高层结构的ETABS 三维模型，并进行了模态分析(图4)。MSC.MARC 模型与ETABS 模型的周期对比误差均在8%以内，验证了MSC.MARC 模型的可靠性。后续抗倒塌性能分析均基于MSC.MARC 模型开展。

2 抗倒塌性能分析

2.1 抗地震倒塌能力分析

采用IDA 方法评估此超高层结构的抗地震倒塌性能。IDA 方法在抗震研究中被广泛采用[19-20]。本文基于该超高层建筑所在地罕遇地震反应谱，选取了8 组地震动记录(包含2 组人工波和6 组天然波)作为有限元模型的基本输入，逐步增大地震动强度，直至结构发生倒塌。8 组地震动记录来自于该栋超高层的结构设计阶段所采用的地震动集合。每组地震动记录包含两个水平方向记录和一个竖直方向记录，8 组地震动记录的反应谱如图5所示，各地震动记录时长达到结构第一周期的5 倍～10 倍。

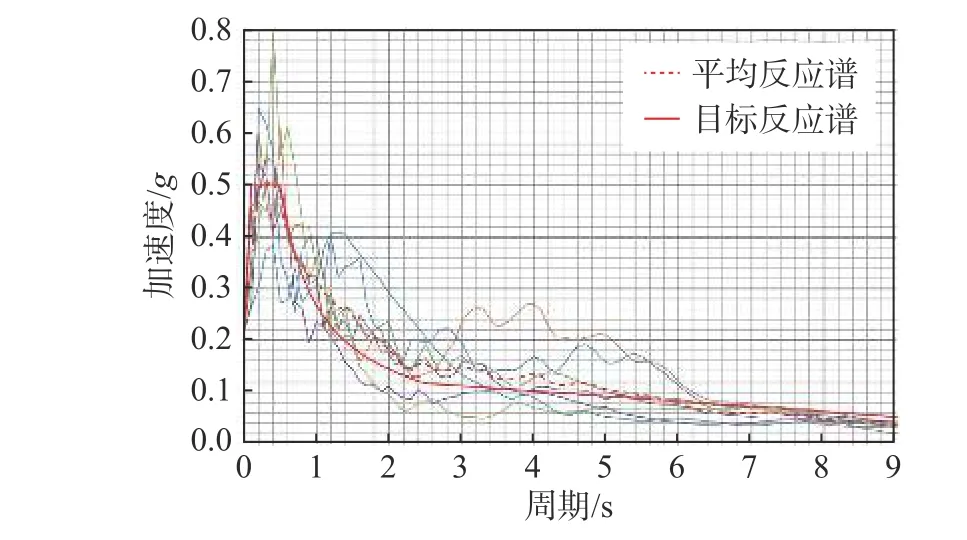
图5 地震动反应谱Fig.5 Response spectra of selected ground motions

依据《建筑抗震设计规范》(GB 50011-2010)[18]，本研究选用地面峰值加速度PGA(peak ground acceleration)为IDA 方法的地震动强度指标。采用三向输入，三个方向地震动强度比值为1∶0.85∶0.65。对于每组地震动记录，考虑两种主次方向情况，取两种情况下倒塌临界PGA 的较小值作为该组地震动记录下的最终倒塌临界PGA。阻尼采用经典的Rayleigh 阻尼，阻尼比取5%。

采用“结构不能继续维持保障人员安全的生存空间”作为结构倒塌的判别指标[13,21]。8 组地震动记录下该超高层结构倒塌临界地震动强度及破坏位置的分析结果如表2 所示，对应的倒塌模式示意图如图6 所示。由此可得其地震倒塌易损性曲线如图7 所示。

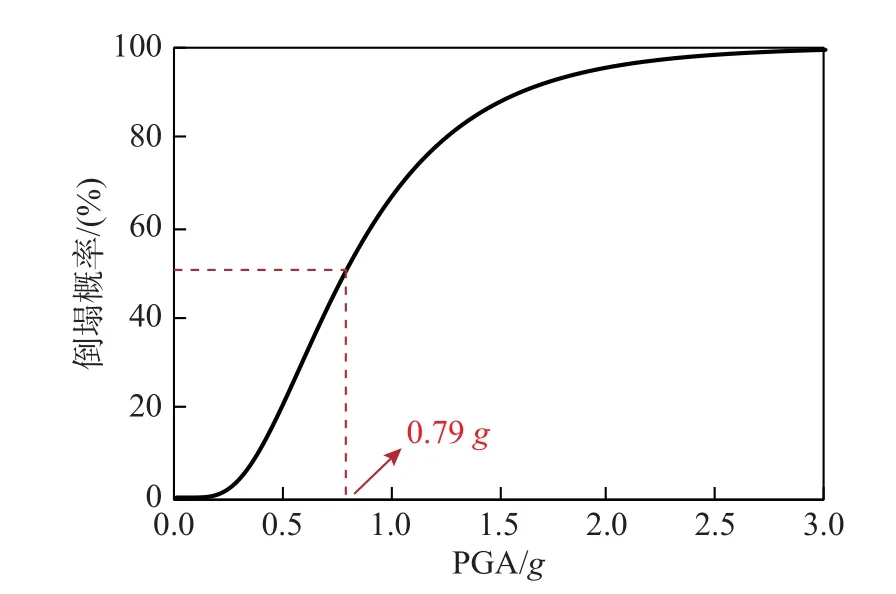
图7 地震倒塌易损性曲线Fig.7 Seismic collapse fragility curve

8 组地震动记录下，结构倒塌临界PGA 均值约为0.91g，结构10%倒塌率所对应的PGA 约为0.39g，结构50%倒塌率所对应的PGA 约为0.79g。该超高层结构设防烈度为7 度，罕遇地震PGA罕遇为0.22g。由此可得50%倒塌率所对应的抗倒塌安全储备系数CMR50%为0.79/0.22=3.59。可见，该超高层结构抗倒塌安全储备较高，具有良好的抗大震性能。

此外，可以看出不同地震动记录下初始倒塌部位主要集中在Zone 6 和Zone7 节段，Zone 6 区域倒塌模式最为普遍。在地震动记录5 和记录6下，结构初始倒塌部位位于Zone 7；而在其他地震动记录下，结构初始倒塌部位位于Zone 6。这是因为地震动记录5 和记录6 的长周期分量较其他地震动记录明显更为显著，更容易激发结构的一阶振型，使得Zone 6 的响应较Zone 7 更为显著。

下面以地震动记录7 和记录6 下的倒塌过程对Zone 6 和Zone 7 区域典型倒塌模式进行介绍。

1) 地震动记录7，倒塌部位Zone 6

如图8 所示：Zone 6 底部楼层东南角剪力墙在17.11 s～19.82 s 开始发生破坏；随后在22.22 s时，Zone 6 底部楼层东南角剪力墙形成了大面积破坏，并促使该楼层其余位置剪力墙和上下相邻楼层该角落剪力墙也陆续发生破坏；在24.00 s时，Zone 6 底部楼层剪力墙破坏殆尽，仅有西南角少数剪力墙未退出工作；最后，Zone 6 底部楼层8 根巨柱在32.88 s～34.21 s 陆续发生破坏，上部楼层坠落，整体结构发生倒塌。

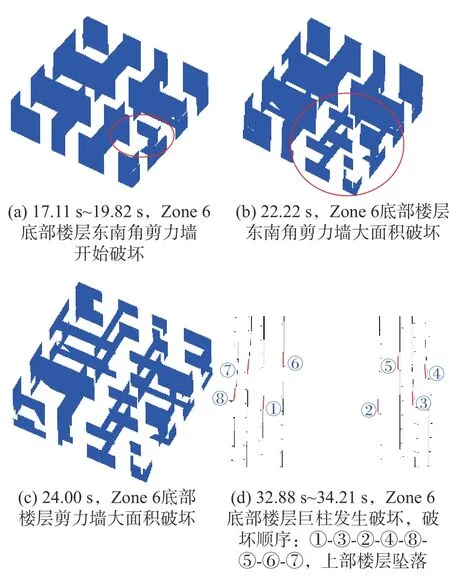
图8 地震动记录7 下关键构件破坏顺序 (PGA = 0.75g)Fig.8 Failure sequence of key components under No.7 ground motion (PGA = 0.75g)

Zone 6 节段位于结构两个伸臂桁架层的中间，可能形成薄弱层。且Zone 6 节段底部楼层巨柱为了配合建筑体型收进存在明显倾斜。此外，Zone 6 节段的外围框架采用“半吊半坐”设计，常规外围框架在某根框架柱失效情况下还能通过框架柱的抗拉实现重力重分布，而原本就“吊”着的框架在框架柱失效后不存在第二条传力路径，本质上是为了建筑设计需要而放弃了一条备用传力路径，这可能部分程度影响了结构的整体抗倒塌性能。上述因素可能是倒塌部位集中在Zone 6 节段底部楼层的原因。

2) 地震动记录6，倒塌部位Zone 7

如图9 所示：Zone 7 底部第二层南侧剪力墙在36.52 s～38.27 s 开始发生破坏；随后在41.20 s～44.49 s 时，Zone 7 底部第二层东南角剪力墙形成了大面积破坏，并促使该楼层西侧和东北角剪力墙也陆续发生破坏；在49.10 s 时，Zone 7 底部第二层剪力墙几乎全部退出工作；最后，Zone 7 底部第二层5 根巨柱在55.60 s～58.43 s 陆续发生破坏，上部楼层倾倒，整体结构发生倒塌。

图9 地震动记录6 下关键构件破坏顺序(PGA = 0.40g)Fig.9 Failure sequence of key components under No.6 ground motion (PGA = 0.40g)

Zone 7 节段位于第二道伸臂桁架层上方，且该节段剪力墙存在明显斜向缩进，可能形成薄弱层。上述因素可能是倒塌部位也或有发生在Zone 7 节段的原因。

2.2 抗爆能力分析

考虑超高层建筑所处的地理位置和实际情况，本文主要针对两种可能的爆炸情景(即箱包炸弹和面包车炸弹)开展分析。由于结构布置较为方正规整，不妨假定爆炸发生在结构西侧(如图10)。依据《民用建筑防爆设计标准》(T/CECS 736-2020)[22]来确定两种爆炸情境的爆炸荷载。

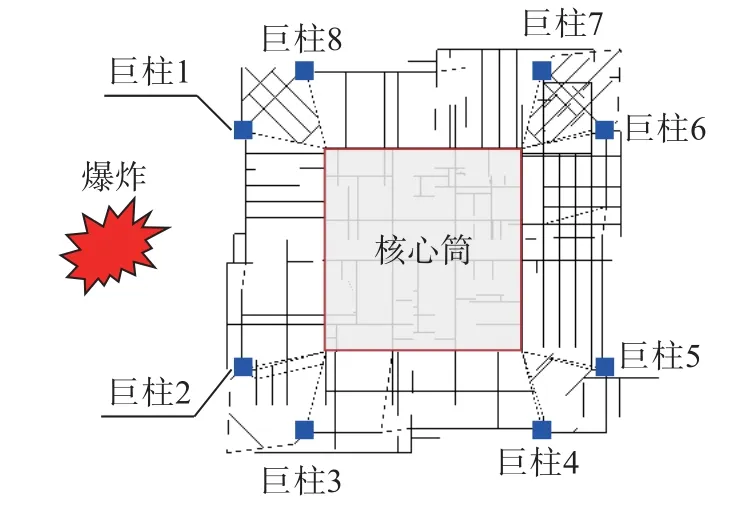
图10 假想爆炸位置Fig.10 Hypothetical explosion location

1) 箱包炸弹，炸药类型PBX-9404，爆炸源距西侧墙面5 m。

依据《民用建筑防爆设计标准》，箱包炸弹TNT 当量为25 kg。考虑较不利情况，假定炸药类型为烈性较强的PBX-9404，则TNT 当量折算系数为1.7，TNT 当量折算后为42.5 kg。在爆炸源距西侧墙面5 m 情况下，采用如下方法计算爆炸荷载：考虑只有底部两层(高度16.5 m)承担爆炸荷载，得到建筑西侧墙面上的爆炸压强如图11 所示。进一步假定施加到建筑墙面上的冲击波压强均无损耗地传递至结构西侧的两根巨柱上，则基于西侧墙面面积可得到：每根巨柱承担的爆炸超压正压产生的荷载峰值为1.70×106kN，爆炸超压负压产生的荷载峰值为3.39×104kN。

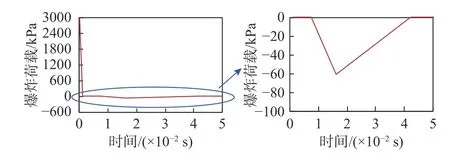
图11 西侧墙面爆炸压强(箱包炸弹)Fig.11 Explosion pressure on the west wall (luggage bomb)

实际情况下爆炸冲击波首先作用于建筑墙面，由外围玻璃幕墙等非结构构件耗散部分爆炸能量后才进而传递到结构外周框架梁和巨柱上，因此上述爆炸荷载计算方法偏于保守，得到的爆炸荷载要大于真实情况。

采用同样方法可计算结构其他方向巨柱的爆炸荷载。由于依据《民用建筑防爆设计标准》计算得到的建筑南、北侧爆炸超压正压作用峰值太小(不超过1.5 kPa)，东侧爆炸超压正压作用峰值更小，其影响可以忽略不计，因此，本文暂时不考虑除西侧墙面外其他墙面的爆炸荷载。

2) 面包车炸弹，炸药类型PBX-9404，爆炸源距西侧墙面10 m。

面包车炸弹TNT 当量为500 kg，假定炸药类型为烈性较强的PBX-9404，TNT 当量折算后为850 kg。在爆炸源距西侧墙面10 m 情况下，采用与箱包炸弹爆炸荷载相同的计算方法，得到建筑西侧墙面上的爆炸压强如图12 所示。西侧每根巨柱承担的爆炸超压正压产生的荷载峰值为4.52×106kN，爆炸超压负压产生的荷载峰值为4.52×104kN。类似地，此爆炸荷载较真实情况偏大。

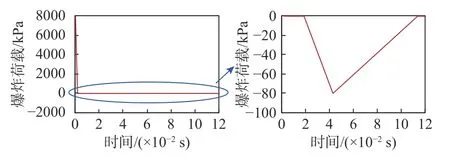
图12 西侧墙面爆炸压强(面包车炸弹)Fig.12 Explosion pressure on the west wall (van bomb)

先对结构施加重力荷载，而后将上述爆炸荷载施加到结构有限元模型上进行动力时程分析，时间步长取0.0001 s。两种爆炸情境下，30 m 以下西侧两根巨柱的侧向位移结果如图13 所示。

图13 西侧巨柱的侧向位移Fig.13 Lateral displacements of west columns

在箱包炸弹下，巨柱在爆炸冲击波方向的峰值位移约为0.7 mm；在面包车炸弹下，巨柱在爆炸冲击波方向的峰值位移约为4.0 mm。通过峰值位移最大位置处的位移时程曲线可以看出：在重力荷载下，巨柱有微小侧向位移；当爆炸发生后，巨柱先是在超压正压作用下迅速达到峰值位移；而后在超压正压和负压的间隙以及在超压负压作用下，巨柱侧向位移逐渐回到重力荷载下的水平，并在该位移水平附近微小振动。主结构在两种爆炸情景下均未发生破坏。通过对构件的应力和应变水平进行检查，发现所有构件均未出现塑性铰。

可见，结构的抗爆能力满足《民用建筑防爆设计标准》。为了进一步检验结构在爆炸荷载下的抗倒塌能力，将箱包炸弹和面包车炸弹TNT 当量持续增加，计算不同TNT 当量下结构的响应，直至结构的西侧巨柱发生破坏，得到西侧巨柱峰值侧向位移与TNT 当量的关系如图14 所示。在爆炸距离为5 m 的情况下，箱包炸弹的TNT 当量达到约3.2 t 时可以造成建筑西侧的巨柱失效；在爆炸距离为10 m 的情况下，面包车炸弹的TNT当量达到约10.0 t 时可以造成建筑西侧的巨柱失效。在建筑西侧的巨柱1 和巨柱2 失效后，由于南侧和北侧靠近爆炸点的巨柱(即巨柱3 和8，图10)也同时遭遇一定损伤，最终导致结构发生倒塌。

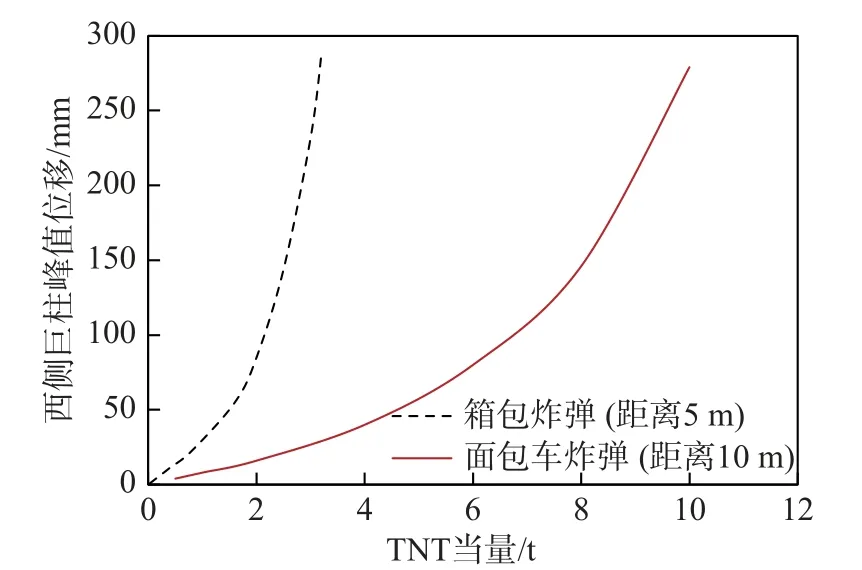
图14 巨柱峰值侧向位移与TNT 当量的关系Fig.14 Relationship between peak lateral displacement of mega column and TNT equivalent

2.3 基于拆除构件法的抗连续倒塌能力分析

在上述抗爆能力分析基础上，进一步基于拆除构件法[23-24]对该超高层结构的抗连续倒塌能力进行评估。考虑拆除该结构主要抗侧力体系中的关键竖向构件，包括巨柱、顶部钢框架柱以及次级钢框架中的钢柱，并对剩余结构进行动力有限元分析以考察抗连续倒塌性能。基于结构设计方案，考虑以下拆除构件工况：

1) 工况1 为拆除底层轴压力较大的巨柱，监测原巨柱顶点位置处的位移变化；

2) 考虑到在IDA 分析中不同地震动记录下结构倒塌部位多集中于Zone 6 节段的底部楼层，故工况2 为拆除Zone 6 节段底部楼层轴压力较大的巨柱，监测原巨柱顶点位置处的位移变化；

3) 工况3 为拆除顶部钢框架塔冠底层的钢柱，监测原钢柱顶点位置处的位移变化；

4) 工况4 为拆除Zone 1 环带桁架层下方次级钢框架的吊柱，监测原吊柱底部位置的位移变化；

5) 工况5 为拆除Zone 2 底部楼层次级钢框架的承重柱，监测原承重柱顶端位置的位移变化；

6) 工况6 为拆除Zone 7 底部楼层次级钢框架的承重柱，监测原承重柱顶端位置处的位移变化。

先对结构施加重力荷载，而后在有限元模型中将上述工况中的拟拆除构件“杀死”，并进行重力荷载工况下的动力时程分析。时间步长取0.005 s。六种工况下监测点的竖向位移变化如图15所示。

图15 监测点竖向位移Fig.15 Vertical displacements of monitoring points

1) 工况1 下：巨柱柱头在拆除构件后迅速从重力荷载工况位置向下位移约95 mm。由于周围钢框架梁与巨柱采用刚性连接，存在备用传递路径，柱头之后在周围钢梁拉结力下竖向位移有所减少，并随着时间在约92 mm 竖向位移处上下轻微振动。

2) 工况2 下：巨柱柱头在拆除构件后迅速从重力荷载工况位置向下位移约50 mm，之后在周围构件拉结力作用下随着时间在约89 mm 竖向位移处上下轻微振动。

3) 工况3 下：钢柱柱头在拆除构件后位移迅速达到约73 mm，由于上部钢框架重力较小，柱头位置很快达到重力新平衡状态。

4) 工况4 下：在拆除次级钢框架吊柱后，原柱底位置处竖向位移达到约55 mm。由于次级钢框架的梁、柱采用刚性连接，存在备用传递路径，柱底之后在周围次级钢框架梁拉结力下竖向位移有所减少，在约49 mm 位移处振动数下后达到平衡。

5) 工况5 下：在拆除次级钢框架承重柱后，原柱头位置竖向位移达到约57 mm，之后在周围次框架梁拉结力作用下竖向位移有所减少，在约50 mm 位移处振动数下后达到平衡。

6) 工况6 下：次级钢框架承重柱柱头在拆除构件后位移达到85 mm，之后很快达到新平衡状态。

由于外周巨型框架梁与巨柱采用刚性连接，次级钢框架的梁和柱亦采用刚性连接，因此在巨柱、钢柱等构件被移除后，结构可以通过备用传递路径实现重力重分布，达到新的平衡状态。通过对构件的应力和应变水平进行检查发现所有构件均未出现塑性铰。可见，在只拆除一根竖向构件的情况下，结构整体抗连续倒塌性能良好。

从图15 观察到底层巨柱对于结构的抗重力体系影响较大，进一步研究同时拆除两根底部巨柱和同时拆除三根底部巨柱情况下结构是否会发生倒塌。结果如表3 所示。巨柱编号见图10。可以看出；在拆除两根底部巨柱的情况下，结构由于富余的传力路径均未发生倒塌；在拆除三根底部巨柱的情况下，若拆除的巨柱不是建筑相邻角四根巨柱的三根，则结构依然可以不发生倒塌，反之则发生倒塌。这是因为当拆除掉建筑相邻角四根巨柱的三根巨柱时，结构存在接近一半面积的重力荷载无法得到有效支撑，从而使得结构在该区域竖向变形过大而发生倒塌。上述结果为结构在构件拆除情况下的极限抗倒塌能力的确定提供了一定依据。

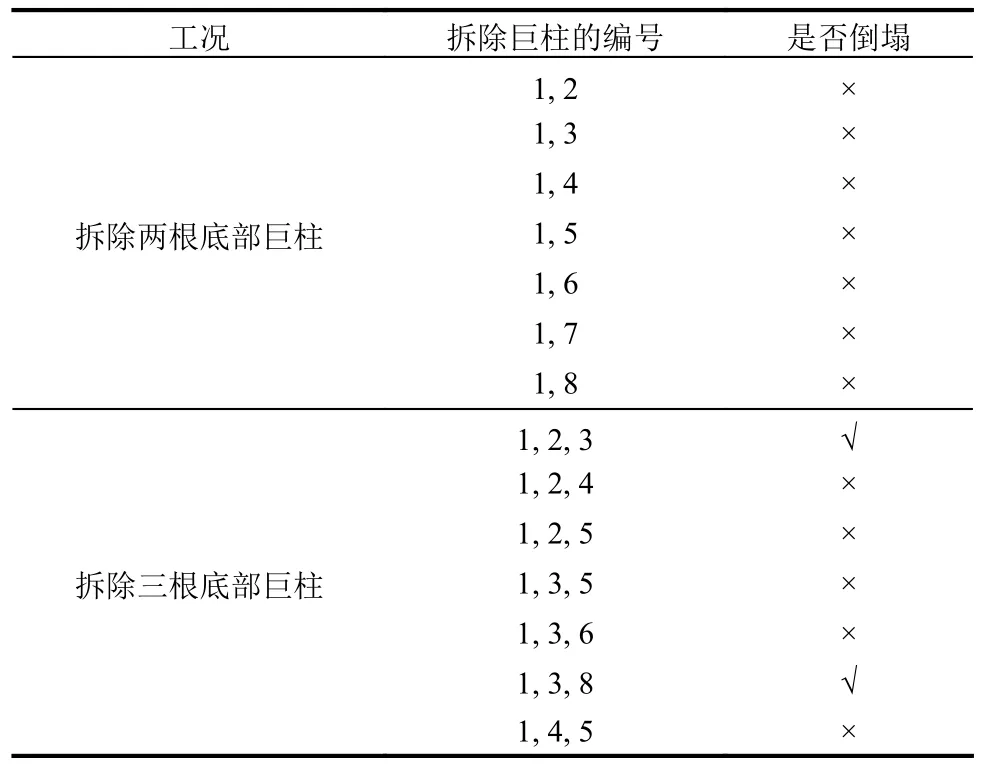
表3 底层巨柱拆除工况下结构倒塌情况Table 3 Structure condition under the removal of bottomstory mega columns

3 结论

超高层建筑的抗倒塌设计是其安全设计中的重要一环，保障超高层建筑的抗倒塌性能对于保护人民生命财产安全具有重要意义。本文对7 度区一489 m 超高层结构的抗地震倒塌和抗连续倒塌能力进行了分析，结果表明：

(1) 在所选8 组地震动记录下，结构的CMR50%约为3.59，抗倒塌安全储备较高，具有良好的抗地震倒塌性能；倒塌部位主要集中在Zone 6 和Zone7 区段。

(2) 在爆炸距离为5 m 的情况下，箱包炸弹的TNT 当量达到约3.2 t 时可以造成建筑承受爆炸冲击波的一侧巨柱失效，从而导致结构发生倒塌；在爆炸距离为10 m 的情况下，面包车炸弹的TNT当量达到约10.0 t 时可以造成建筑承受爆炸冲击波的一侧巨柱失效，从而导致结构发生倒塌。

(3) 在巨柱、塔冠钢柱、次级钢框架吊柱和承重柱等关键竖向构件中的一根构件被拆除后，结构备用传递路径能够发挥作用，整体结构抗连续倒塌性能良好。底层巨柱的拆除对于结构的抗重力体系影响较大。

(4) 在拆除两根底部巨柱的情况下，结构由于富余的传力路径均未发生倒塌；在拆除三根底部巨柱的情况下，若拆除的巨柱不是建筑相邻角四根巨柱的三根，则结构依然可以不发生倒塌，反之则发生倒塌。

本文分析方法和结果可以为类似超高层建筑的防倒塌设计提供参考和借鉴。