混合监测方法在桥梁静载试验中的应用
2024-04-11李煦阳张玮赵长军孙利民
李煦阳, 张玮, 赵长军, 孙利民
(1.浙江数智交院科技股份有限公司, 浙江 杭州 310030;2.同济大学 土木工程学院, 上海 200092;3.福建省建筑工程质量检测中心有限公司, 福建 福州 350028;4.福建省绿色建筑技术重点实验室, 福建 福州 350001)
0 引言
获得结构全面而准确的数据信息是桥梁健康监测的重要目的之一,也是损伤识别及状态评估的基础,然而现有结构健康监测(structural health monitoring,SHM)系统的传感器数量无法覆盖整座桥梁,并由此导致:①部分物理量因监测难度大而被舍弃,造成监测信息不全面;②受限于成本,为监测更多种类的物理量不得不牺牲同类型传感器数量;③受限于空间,同一个监测点位难以安装多种传感器,导致不同物理量所对应的位置大都不同,给数据融合带来阻碍。多源信息融合作为一门新兴的交叉学科,目的是通过信息组合推导出更多的信息,从而获得更佳的协同作用结果[1]。桥梁SHM系统中的多源信息融合技术包含了数据级融合、特征级融合和决策级融合3个层面,融合算法也是多种多样,一般可分为随机算法和人工智能方法2类[2]。聂功武[3]在调研我国大跨度桥梁养护管理现状的基础上,提出了SHM数据与巡检养护信息融合的框架。Zonta等[4]将磁通量传感器数据与光纤传感器数据融合,提高了斜拉桥索力的测量精度。Cho等[5]利用应变及加速度数据,并融合有限元模型的计算模态,估计出了桥梁的动挠度。Liu等[6]研究了人工检测和长期监测数据的融合方法,用于判断斜拉桥的异常索力。总的来说,多源信息融合在桥梁SHM中的应用仍处于起步阶段,且研究范围多集中在索力、线型及损伤识别等少数几个方面,要想获得全面、准确的结构状态信息仍比较困难。
为了解决上述问题,本文尝试通过数值方法从有限的实测数据推算出未测信息,进而整合成部分实测、部分计算的完备结构信息,即混合监测技术。上述设想来源于20世纪90年代兴起的混合试验技术(hybrid test)[7]。混合试验技术将试验对象分为试验子结构和数值子结构2个部分,其中试验子结构是结构中构造复杂、难以数值模拟的部分,数值子结构是结构中构造简单明确、容易数值模拟的部分,二者通过作动器实现力与位移的相互传递,可获得整个结构的整体响应和局部响应,从而减少试验工作量,降低试验成本。早在20世纪90年代,Nakashima等[8]和Shing等[9]就先后实现了完整的拟动力混合试验流程。针对速度相关型构件的特点,Nakashima等[10]又发展出了实时混合试验技术,该技术要求位移命令能实时地通过作动器作用于试验子结构上,而数值子结构需要考虑地震引起的惯性力。1999年,美国国家科学基金委员会投资8 200万美元建立地震工程网络模拟系统(network for earthquake engineering simulation, NEES),以整合分散的设备站点以促进地震工程的研究及教育领域的合作[11]。在NEES数据库中,至少有29个项目采用了混合模拟试验方法从事相关研究,李歆等[12]对此进行了详细的总结。与此同时,全球各个地区也纷纷推进自己的混合试验平台,例如欧洲的欧洲网络EUROSEISMICNET、日本的E-Defence及并行混合试验网络、韩国的KOCED项目以及中国台湾的ISEE平台[13]。此后,混合试验技术得到了长足的进步,研究对象也逐步发展到钢筋混凝土结构、木质剪力墙、多跨连续梁桥墩及新型阻尼器系统等多种复杂结构上[14-15]。2008年,湖南大学、哈尔滨工业大学和清华大学等成功进行了国内首次多跨桥梁的远程协同拟动力实验,分析了2根碳纤维复合材料CFRP加固剪切柱在地震荷载作用下的破坏现象、延性及耗能[16]。何政等[17]详细讨论了OpenSees混合模拟试验技术发展与应用,证明了基于商业或非商业有限元软件平台开展混合模拟试验是可行的。陈再现等[18]采用混合编程方法建立了基于MATLAB和OpenSees的子结构混合模拟试验系统,进一步减少了对控制系统本身的要求,降低了试验难度和费用。
类似于混合试验,混合监测的核心理论是在经典结构平衡方程基础之上借助修正后的有限元模型,先从测得的响应数据反推荷载信息,再根据等效荷载计算出全结构响应。该方法可实现同类型数据的扩充,以及不同数据类型间的转换、分离与融合。本文重点推导混合监测静力学理论并应用到实桥静载试验,为逐步完善与深化相关理论提供参考。
1 混合监测理论
1.1 广义平衡方程的简化
经典结构动力学框架下任意时刻t的结构平衡方程为
(1)
式中:M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;
和v分别为结构的加速度、速度和位移向量;P为结构的外部荷载。将位移向量v移到方程左侧可得
(2)

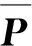
1.2 柔度矩阵的提取
现以梁式桥有限元模型为例说明柔性矩阵的求解过程,假设桥上车辆荷载用竖向集中荷载P(xi)近似,其中xi(i=1,2,…,n)为各节点坐标。P(xi)主要引起梁体下挠,所以关心的自由度应为各节点沿竖向的挠度w(xi)。假定梁体安装N(N≪n)个位移计,每个节点的竖向挠度监测值为w(xi)(xi为测点坐标,i=1,2,…,N), 梁式桥在车辆荷载作用下的有限元模型如图1所示。
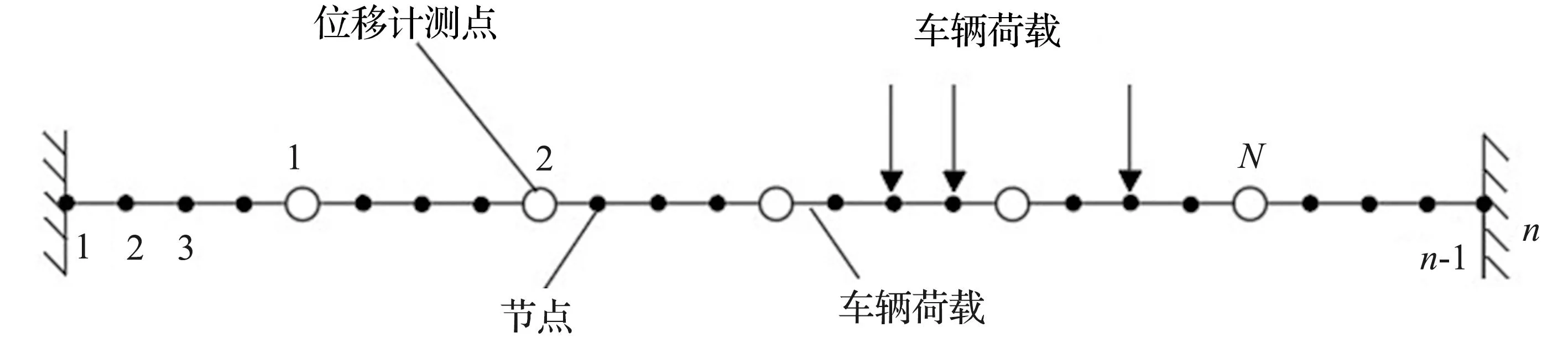
图1 梁式桥在车辆荷载作用下的有限元模型Fig.1 Finite element model of beam bridge under vehicle load
现提出上述场景下的混合监测问题。车辆荷载作用下,如何利用N个位移计实测挠度值计算梁体所有n个节点挠度,这样所提取的柔度矩阵必须能够反映竖向荷载与挠度的关系。对节点进行挠度影响线分析,即可得到行向量(d1(xi),…dj(xi),…dn(xi)),其中dj(xi)表示竖向单位力作用在xj处时xi处节点产生的挠度值。所有n个节点的挠度影响线可组成n×n型挠度柔度矩阵,记为D,即
类似地,对于其他型式桥梁也可通过有限元模型将竖向单位力作用在梁体各节点,并逐次记录梁体所有节点的竖向挠度值,从而获取该桥梁的柔度矩阵。矩阵D中每一列代表单位力作用在梁上某一点时梁上所有点产生的竖向挠度值。竖向挠度矩阵w、D与P之间的代数关系为
wn×1=Dn×nPn×1。
(3)
受传感器数量限制,实际监测的位移值仅有w=[w(x1),w(x2),…,w(xN)]T。为了使式(3)成立,需要删除D矩阵中多余的行,得到
(4)
即:
wN×1=DN×nPn×1。
(5)
由于未知数的个数n远大于方程的数目N,因此式(5)为欠定方程组。下面需要从该方程组的无穷多组解中确定一组解作为等效荷载。
2 基于偏最小二乘回归(PLSR)的混合计算
2.1 PLSR 计算流程
由于实测信号中存在误差,因此式(5)应改写为
(6)

yN×1=XN×nβn×1+eN×1,
(7)
式中yN×1、XN×n、βn×1和eN×1分别对应结构实测响应、柔度矩阵、荷载和测量误差。显然上式可使用回归分析中的相关算法去求解。引入偏最小二乘回归(partial least square regression,PLSR)算法来求解方程组(7)。
作为第二代回归分析方法,PLSR 主要研究多因变量对多自变量的回归建模,当自变量集合内部存在较高程度的相关性时,PLSR比逐个回归更加有效。该方法首先进行相关性分析,然后通过主成分分析简化数据结构,最后利用多元回归分析建立回归方程。用该方法可以计算得到对因变量解释性最强的综合变量,消除多重相关性并分辨出噪声与信息,实现自变量个数大于样本点个数时的建模分析。
PLSR分析的第一步是要从X和y中提取隐变量[即偏最小二乘(PLS)成分]。具体步骤如下:
① 对X和y进行标准化计算,使每列的均值为0,方差为1,标准化后的矩阵分别为X0和y0。
② 从y0中抽取1个成分u1,由于y0是列向量,因此u1=y0。
③ 从X0中抽取1个成分t1,令t1=X0w1,且‖w1‖=1。其中w1可以通过式(8)求出:
(8)
④ 对X0在t1上和y0在t1上进行线性回归分析:
(9)
y0=t1r1+y1,
(10)
其中:X1和y1是残差矩阵;p1和r1是回归系数,
(11)
⑤ 将原矩阵X0和y0用残差矩阵X1和y1进行替换,接下来重复(2)—(4),即得新的回归系数p2和r2以及新的残差矩阵X2和y2。
⑥ 继续重复(2)—(5)提取出所有所需的成分。
2.2 荷载估计
假定已经从X0中提取出p个成分(t1,t2,…,tp),则可建立响应y0与PLS成分之间的多元线性回归模型
y0=u1=r1t1+r2t2+…+rptp+yp,
(12)
写成矩阵的形式为
y0=Tr+yp。
(13)
多重共线性矩阵X0的秩要大于提取的成分数p,即p r=(TTT)-1TTy0。 (14) 由于t1、t2、…、tp是X0中向量的线性组合,系数矩阵为W,那么得 (t1,t2,…,tp)=T=X0W=X0(w1,w2,…,wp)。 (15) 解出回归系数r后再将式(15)代入式(13)得 y0=Tr+yp=(X0W)r+yp=X0β0+yp, (16) 式中β0为标准化后自变量矩阵和观测矩阵的回归系数,通过β0=Wr求解得出。 (17) 综上,通过引入PLSR方法不但解决了欠定结构平衡方程的求解问题,而且能直接计算出全结构响应,避免进行多次有限元计算。整个荷载估计和响应计算过程只涉及矩阵间的数值运算,因此可达到毫秒级计算效率,使实时计算成为可能。完整的混合计算流程如图2所示。该流程具有以下特点:①直接从有限元模型中获取结构信息,避免对插值基函数进行假定和选择,也能更好地适应复杂空间结构;②等效荷载通过回归系数表示,因而具有明确的物理意义;③方程形式和计算过程简单明了,可拓展性强。 图2 混合计算流程Fig.2 Flow chart of hybrid computing 本项研究的工程背景是山区环境中的一座新建系杆拱桥,采用钢管混凝土拱肋-钢箱系杆-钢结构横梁的结构形式。桥梁静载试验利用有限元分析程序 Midas Civil 进行建模分析,钢管混凝土内部、拱脚、混凝土预制板、调平层、湿接缝、现浇桥面板等采用强度等级为C50补偿收缩混凝土,弹性模量均取34 500 MPa,拉索钢绞线标准强度取1 860 MPa,弹性模量取1.95×105MPa,最终建立的依托工程有限元模型如图3所示。 图3 依托工程有限元模型Fig.3 Finite element model of supporting project 实桥静载试验主要测试在相当于设计汽车荷载最不利效应的等效试验荷载作用下,各主要控制截面的应变(应力)、挠度(变位)、吊杆拉力以及典型结构性裂缝和典型质量较差焊缝的发展、闭合情况。为了保证各主要测试截面试验荷载效率系数不小于0.85,计算确定静载试验需用450 kN(车重及荷重)载重汽车共8辆。现场加载车配重时整车重量的允许误差为±10 kN。根据各测试截面的内力与挠度影响线,选定静载试验的各主要测试截面如图4所示。 图4 静载试验主要测试截面Fig.4 Main test sections for static load test 本研究首先根据某静载试验工况实测数据对有限元模型进行修正(不在本文阐述),然后根据混合监测理论进行混合计算。该工况下4辆加载车纵桥向按拱肋和系梁的截面正弯矩最不利位置布载,横桥向为中载布置,在拱肋和系梁的1/4、1/2、3/4截面分别布置1个挠度测点,共计6个挠度测点。 上述静载试验工况中实测得到系梁和拱肋的静载试验实测挠度值见表1。 表1 静载试验实测挠度值Tab.1 Measured deflection value in static load test 表2 结构柔度矩阵转置Tab.2 Transposition of structural flexibility matrix mm 利用挠度实测值和挠度柔度矩阵建立方程,并通过PLSR估计出等效荷载(取成分数为9),等效荷载与实际荷载的对比如图5所示。由图5可见,等效荷载与实际荷载分布十分接近,但PLSR方法估计出的等效荷载只是一组近似解,与实际荷载仍有区别。混合监测中等效荷载仅作为中间变量,只要后续计算出的结构响应与实测值接近,就能证明该过程具有意义。 图5 等效荷载与实际荷载对比Fig.5 Comparison between equivalent load and actual load 将等效荷载与挠度柔度矩阵相乘,就可得到全结构所有节点的挠度计算值,其结果如图6所示。由图6可见,挠度计算响应值与实测响应值的最大误差不超过10%,很好地验证了通过等效荷载计算结构响应的可行性。另外注意到,计算响应值均比实测响应值偏小,这是由于结构实际刚度比计算模型偏大,因此导致计算所得等效荷载偏小。 图6 计算响应与实测响应对比Fig.6 Comparison between calculated response and actual response 本文将混合监测技术应用到系杆拱桥静载试验,有限元模型、SHM系统和回归分析算法构成了混合监测方法的核心,其中:监测系统采集结构的实时信息,为有限元模型修正和回归分析提供实测数据;修正后的有限元模型可以反映结构状态,并能提供结构柔度矩阵等关键信息;回归分析可以避免重复的有限元计算,通过方程的快速求解来有效补充监测数据。得到以下主要结论: ① 忽略动力响应和结构阻尼是经典结构平衡方程简化的前提假定,结果证明,经过简化的结构平衡方程可较为准确地描述系杆拱桥在静载作用下的响应。 ② 利用偏最小二乘回归法(PLSR)计算等效荷载可解决欠定结构平衡方程组的求解问题,虽然PLSR求出的等效荷载不是真实作用在结构上的荷载,但仍可较为精确地计算结构响应,本文算例中计算响应与实际响应误差均在10%以内。 ③ 混合监测方法实现了结构静力指标从部分响应数据到全局响应数据的扩展,且计算效率较高,避免了反复的有限元分析,进而可为桥梁健康监测工程的轻量化设计提供理论依据。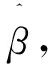
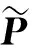
2.3 全结构响应计算
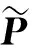

3 应用实例
3.1 工程概况


3.2 混合计算



4 结论
