初中数学课堂中变式教学法的应用——以“一元二次方程”为例

文| 武金燕

变式教学法指的是对数学问题进行合理转化的一种方法，在转化的过程中需分析数学知识之间的关联，在此过程中学生的数学思维可以得到有效锻炼，使学生明确数学概念，加强对知识的实际应用。同时，变式教学法需要教师发挥学生的主体作用，引导学生在解答变式题的过程中对数学概念、相关知识进行深度理解，从而提高学生的自主建构能力，对学生有着深远的影响。

一、初中数学变式教学法应用的关键点和原则

（一）初中数学变式教学法应用的关键点

初中数学教师在进行变式教学时需要引导学生细致剖析问题，再建构变式题组，要求学生充分理解该部分知识。在开展变式教学活动的过程中，对数学问题进行精细化拆分时，教师要让学生注意两点：一是从问题中提炼出必要条件，做好标注；二是梳理解题思路和处理目标，明确问题的答案。教师应以数学概念、图形为着手点展开变式训练，根据原题适当调整条件和结论，让学生从多个角度出发理解知识，帮助学生构建具有变通性特征的数学思维模型，促使学生的综合解题能力得到提升。

（二）初中数学变式教学法的原则

一是启迪思维原则。在初中数学变式教学法中，教师应引导学生发散思维、转化思维，根据具体数学问题合理变式，使学生的思维一直处于活跃状态。教师需要遵循启迪思维原则，通过问题激发学生从不同侧面对问题展开思考，以激发学生的思维活跃度。二是暴露过程原则。学生只有明确解答问题的思维流程才能真正解决数学问题，这也会让学生产生成就感，激发学生的自主学习动力。故而，在具体实践中教师应遵循“暴露过程原则”，将思考问题时的数学思维暴露在学生面前，让学生了解具体的推理过程，掌握数学概念、定理的推导方法，再由教师根据数学题目进行变式，为学生提供新思路，发展学生的数学思维水平。三是探索创新原则。在变式过程中教师需要遵循探索创新原则，以新颖的方法和问题调动学生的积极性，在学生解答问题的过程中启发其思维和心智，强化学生的创新意识。这样学生才能以全局的眼光看待数学问题，发现问题的本质和规律，从而实现对知识的融会贯通。

二、初中数学变式教学法在“一元二次方程”中的应用策略

（一）将概念作为切入点，巩固数学基础

初中数学教学内容中涉及大量的概念性知识，关乎学生思维能力和知识应用能力的发展。数学概念是解答数学问题、推论和论证数学命题的必备条件，在数学概念教学中应用变式教学法可以让学生探究数学概念的本质，以多角度的变式方法对数学概念进行学习和理解，使学生参与到探索概念知识的过程中，从而增强学生思维的灵活性和应变能力。同时，变式教学法能让学生深度理解不同概念的独特属性，在不改变问题本质特征和属性的基础上，以多样化的形式改变部分条件，使学生在解答问题的过程中探索同类问题的规律和解决方法，掌握具体的数学概念。

一元二次方程的相关概念是学生必须掌握的知识，这也是学习和应用一元二次方程解题的前提，教师可以在概念教学中应用变式练习，帮助学生理解所学概念。①下列方程中哪些是一元二次方程：x1）。②写出方程x2+3x-2=0，-2x2-5x+3=0 的常数项、一次项系数以及二次项系数。③将方程式3x2+1=6x，x（x+5）=5x-10，4x2+5x=81 转化为一元二次方程的一般形式，并写出这些方程的常数项、一次项系数以及二次项系数。

学生在完成变式练习的过程中能够对一元二次方程的常数项、一次项系数以及二次项系数的相关概念进行巩固，了解一元二次方程中根与系数的关系，为后续学习一元二次方程的解法奠定基础。

（二）以数学题目为核心，把控变式方向

最近发展区理论指出：学生基础知识的掌握程度会直接影响其最终的学习成果。这就需要教师从学生的基础知识出发，通过剖析数学题目来明确正确的变式方向。初中数学教师应引导学生利用变式联系新旧知识，结合学生的知识基础设计数学题目，通过深入分析题目推动其对基础知识进行更深入的理解，从而实现知识变式，发展学生的思维能力。

一元二次方程有很多解法，这也是学生串联知识时的一个难点，因此，教师应引导学生剖析原题，通过从特殊到一般再到特殊的方法进行合理变式，总结一元二次方程的解法。如原题为：证明代数x2-6x+19 式恒大于0。教师可以引导学生运用一元二次方程四个解法中的配方法求解，再通过变式将该方程转化成含参方程，让学生在解答带有参数的一般化方程的同时总结解法。为了帮助学生巩固基础知识，教师可以让学生将该方程转变为几个类型的特殊一元二次方程，梳理学过的解法。

从以上案例中可知，掌握基础知识并剖析原题是进行变式的前提，教师在进行变式教学法时不仅要引导学生解答数学问题，还要注重指导学生运用掌握的知识梳理新旧知识之间的关联。此题能帮助学生为后续的变式做准备，通过转化平方的形式使用配方法对方程进行配方，使学生对配方法进行学习和总结，有助于学生学习从特殊到一般的变式。

（三）注重学生思维发展，合理设计变式

初中数学教师在开展变式活动时要注重拓展学生的思维空间，提高他们的思维深度。因此，教师应注重合理设计变式，引导学生在变式过程中探究数学知识的本质。教师需要让学生发现知识点之间的关联，看清问题的本质，将特殊规律转变为一般性结论，掌握合理进行变式的方法。

如原题为：已知kx2-3x+1=0，求出k 的取值范围。针对此类题目，教师应引导学生从具体数据过渡到含参方程。该方程的二次项系数含参，因此可能是一元一次方程，若教师没有进行合理变式，会影响学生对前提条件的判断，不利于学生开展分类讨论。因此，教师应把握变式中的固定条件，引导学生对含参方程进行合理变式，加深对一元二次方程的理解。该问题可以变式为：x2+5x-k=0。①已知方程存在两个相等实根，那么k 的取值范围是多少？②已知方程存在两个不等实根，那么k 的取值范围是多少？③已知方程不存在实根，那么k 的取值范围是多少？④已知方程存在实根，那么k 的取值范围是多少？之后教师可以将x2+5x-k=0 变式为kx2-3x+1=0，让学生再次对上述问题进行解答。

初中数学教学中变式教学法占据重要地位，但只有合理设计变式才能让学生从条件中提取关键信息，特别是需要进行分类讨论的问题，只有针对不同情况进行合理变式才能让学生发现问题的本质。需要注意的是，教师在开展变式教学法时要以题目的条件和要求为前提，变式不能与原题出现太大的跨度，也不能和原题相差无几。因此，教师要引导学生串联思路，发现知识点之间的联系，帮助学生吃透知识点。

（四）把握知识逻辑关联，探究知识本质

从特殊到一般的变式能够引发学生的深度思考，让学生明确题目的本质。数学知识之间的逻辑藕断丝连，需要教师引导学生建立联系密切的逻辑网，从整体的角度学习知识。只有加强数学知识之间的联系才更便于学生学习，教师应巩固知识间的逻辑关系，从一般变式到特殊变式，强调学生学习数学知识时的连贯性，促进学生的理解。

例题：选择合适的方法解下列方程：①x2-3x-10=0；②3x2+7x+2=0；③2x（2-x）=3。教师在黑板上写出三个方程：①x2+2x-3=0；②（x+1）2=4；③（x-1）（x+3）=0。

师：请同学们迅速口答出其中一个方程的解。

生1：（x-1）（x+3）=0 的解为1 或-3。

师（进行变式）：（x-m）（x-n）=0 的解是多少？其中m 和n 为常数。

生2：是m 和n。

师（进行变式）：你会采用什么方法求解方程（x+m）2=n（n≥0）？另一个方程呢？

生3：第一个方程可以用直接开平方法，第二个用配方法或公式法都可以。

生4：也可以使用因式分解法，分解为（x-1）（x+3）=0。

师：如果无法使用因式分解法求解一般的一元二次方程，那么可以使用配方法，其目的是什么？

师：你们认为哪种方法更简便？

生（众）：直接用公式更简便。

教师引导学生梳理和归纳一元二次方程的四种解法，即配方法、公式法、直接开平方法以及因式分解法。

可见，教师在发现知识点之间的关联时以变式的形式向学生展现，引导学生运用不同解法求解方程，让学生对比一元二次方程的解法，使学生从本质上理解不同解法的异同点和适用情况，并通过变式串联，从而构建完整的知识网络。

（五）采用情境变式，变更问题情境

情境变式即教师在不改变主线的前提下不断改变问题情境，通过串联不同的问题情境整合课堂教学的各环节。需要注意的是，教师在设计主线时要围绕教学目标铺设，做到串“点”成“线”。在初中数学课堂上开展情境变式教学法能够营造轻松的学习氛围，使学生的思维、想象力在不同的问题情境中得到发展，以提高学生对数学的学习兴趣，打造高效的数学课堂。

为了保证“一元二次方程”的教学效果，教师要对学生进行多角度训练。教师可以创设情境，展开变式教学活动。教师需要先为学生创设故事情境：赵家村的赵大姨不久前承包了一个养猪场，想通过养猪解决经济困难，但因为没有文化遇到了很多问题。希望同学们能够运用数学知识为她提供帮助。赵大姨在后院围了一圈篱笆，其中一面靠墙，准备围出一个猪圈养猪，但却遇到了以下问题。

问题一：赵大姨在后院靠墙围了一个长方形的猪圈（见图1），墙对面的门宽2 m，篱笆的全长为33 m，墙长18 m，已知猪圈的面积是150 m2，请计算猪圈的长和宽。

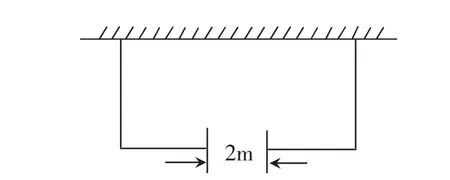
图1

变式1：若不改变问题一中的已知条件，猪圈的面积可以围到200 m2吗？

变式2：若将问题一中的墙长改为xm，会影响猪圈最终的面积吗？

问题二：赵大姨2022 年养猪赚取的利润为2.16万元，2020 年的利润为1.5 万元，若2020 年开始到2022 年的获利增长率不变，她在2021 年赚取的利润为多少？

变式：获利增长率一直不变，赵大姨在2023 年赚取的利润为多少万元？

●习题分析

情境变式能够营造轻松的教学氛围，调动学生的积极性和好奇心，促使学生对数学问题展开深度思考。本次教学设计针对一元二次方程开展，学生融入情境中会迫切希望帮助赵大姨解决问题，以激发学生学习的内驱力。问题一能够让学生对常见的面积问题的解题思路和策略进行巩固；问题二与问题一之间联系密切，能够让学生更好地融入情境中探索变化率问题。

在初中数学教学中运用情境变式需要明确一条主线，也就是串“点”成“线”的教学模式。这样可以通过变式引导学生解决生活中常见的实际问题，从而拓展学生的思维空间，让学生将所学数学知识服务于生活。通过设计情境变式不断改变问题情境，促进学生的思维发展。

总而言之，变式教学法在初中数学教学中占据举足轻重的地位，教师应通过变式教学法打造高效的数学课堂，使学生明确知识之间的关联，构建知识网络。教师需要根据具体的教学内容采用合适的变式方法，将变式教学法与数学知识相融合，引导学生对基本问题进行各类变式，学会举一反三，以增强自身的数学思维能力，为之后的数学学习奠定坚实的基础。