冗余机械臂运动学建模与轨迹规划分析

季晓明

（江苏安全技术职业学院智能制造与应急装备学院，江苏 徐州，221011）

引言

与六轴机械臂相比，冗余机械臂具有多余的操作自由度，可以用来实现机械臂本体的避障、避关节限位、避奇异、优化关节力矩等任务，是当前工业中最常见的一种智能化装备。[1]冗余机械臂运动规划问题一直是学术界的研究热点，它需要通过优化算法或策略来选择合适的机械臂关节运动轨迹，并综合考虑性能指标、工作空间和避免碰撞等条件，从而最大程度地发挥机械臂的灵活性和效率。然而，冗余机械臂的运动学模型较为复杂，尤其是较难获得逆向运动学的解析解法。因此，如何提高冗余机械臂的运动学建模效率和完成其轨迹规划是本文研究的重点。

通常，求解冗余机械臂逆向运动学最多的方法是数值解法。目前，很多学者倾向于利用人工智能优化算法来解决冗余机械臂逆向运动学求解问题，像遗传算法[2]、粒子群算法[3]、萤火虫算法[4]等。然而，这些求解算法具有很强的非线性，实时性较差，不利于机械臂的实际控制。文献[5]只考虑机械臂的主任务和部分约束任务，提出了一种变权重逆向运动学求解算法，获得较高的计算效率。文献[6]采用一种零空间饱和算法来解决冗余机械臂逆向运动学求解问题。文献[7]利用最小二乘法处理机械臂关节约束，从而提高了逆向运动学求解效率。文献[8]在此基础上提出了加权最小二乘法，得到虚拟关节方法，进一步提高了逆向运动学的求解精度。

上述方法为本文的研究提供了很好的借鉴思路。本文拟采用改进的DH 参数法建立冗余机械臂正向运动学模型，首先利用加权最小二乘法获得其逆向运动学模型，接着利用五次多项式对其进行轨迹规划，最后通过仿真算例对本文所提方法的有效性进行验证。

一、运动学建模

本文以类人七自由度冗余机械臂为例，采用改进的DH参数[9]来描述其连杆坐标系，如图1所示。从图1中可以获得该机械臂连杆参数，即连杆长度ai-1、连杆转角αi-1、连杆偏距di和关节角θi。

表1 七自由度冗余机械臂的DH 参数

图1 七自由度冗余机械臂

接着，采用运动学递推方式可以获得7关节坐标系O7X7Y7Z7在基坐标系O0X0Y0Z0的位姿描述，即该机械臂的正向运动学方程为：

一般情况下，冗余机械臂从关节空间到末端执行器操作空间的映射关系可描述为：

式中，θ̇∈R7为机械臂关节角速度矩阵，J ∈R6×7为雅可比矩阵，ẋ∈R6为末端执行器的广义速度矩阵。

如果已知末端执行器的速度轨迹为ẋ，则关节角速度θ̇有无穷多组解，那么采用最小范数解的形式来描述θ̇，即

其中，J†= JT(JJT)-1为雅可比矩阵的伪逆。由于存在冗余自由度，所以可以在完成末端执行器轨迹主运动的基础上参照某些性能指标实现机械臂的自运动，例如关节位置极限、避奇异、避关节速度极限等。很明显，式（4）没有充分挖掘机械臂冗余自由度的操作性能，即存在非零齐次解。因此，在式（4）的右边加上这个非零齐次解，可得：

式中，I7-J†J为雅可比矩阵的零空间矩阵，(I7-J†J)z可实现冗余机械臂的自运动而不影响主运动。z∈R7为任意n维梯度向量，即性能指标函数。对于z的描述有多种形式[10]，例如可构建一种避关节极限性能指标梯度投影法来实现冗余机械臂避关节位置极限或避障，即：

式中，k是权重因子，∇H(θ)是H(θ)的梯度向量。

此外，利用加权最小二乘法同样能实现冗余机械臂避关节位置极限或避障。对雅可比矩阵做如下变换：

式中，Jw与θ̇w分别为加权雅可比矩阵与加权角速度。W∈Rn×n为正定对角加权矩阵，W中的第i个对角元素wi可被定义为：

整理式（3）（8）与（9），可得：

当Jw处于满秩状态时，基于加权最小范数的上式逆向运动学的解可表示为：

很显然，当J接近奇异点或wi过大时，Jw将变得病态。为解决这个问题，在上式中加入一个阻尼因子λ，即：

式中，I∈Rm为单位矩阵。值得注意的是，较小的λ会导致算法在奇异点附近的鲁棒性变低，较大的λ会导致跟踪误差变大，故应根据雅可比矩阵的最小奇异值σmin来选择λ的值：

式中，ε为奇异值阈值，λmax为最大阻尼因子。

根据上述分析，基于梯度投影法的冗余机械臂逆向运动学的解（7）可调整为：

采用加权最小二乘法可将冗余机械臂逆向运动学的解（11）可调整为：

二、轨迹规划算法

对于冗余机械臂的轨迹规划，一般包括关节空间轨迹规划和笛卡儿轨迹规划两种。[11-12]由于笛卡儿轨迹规划要实时计算各路径点的逆向运动学，计算效率低，所以本文选择关节空间轨迹规划。如果已知冗余机械臂的初始状态x0和终止状态xf，先通过差分法获得初始广义速度ẋ0和终止广义速度ẋf，再由式(15)计算出对应的关节角速度，最终通过积分方式获得初始和终止的关节角。

对于冗余机械臂，若已知运动轨迹的起始点与终止点，以及运动过程中各关节处的位置、速度和加速度，便可确定一个五阶多项式插值函数：

上式含有6 个系数a0、a1、a2、a3、a4与a5，则必须满足6个限制条件，即：

求解上式，便可获得五阶多项式插值函数的解为：

三、仿真算例

本节将通过一个运动学仿真算例来验证所提运动学建模方法和轨迹规划方法的有效性。仿真环境为Inter Core i7-4720 HQ，Matlab 2023a。

为了更好地获得冗余机械臂的运动轨迹，先要计算出其工作空间。本文引入蒙特卡罗法[13]随机获得机械臂的可达工作区域，其计算公式为：

式中，randn(·)为具有正态分布特性的随机函数。将获得的随机关节角序列代入式(1)中，就可以获得冗余机械臂大致的工作空间，如图2所示。

图2 七自由度冗余机械臂的工作空间

上图所示的工作空间中用Matlab 自带的标记工具选定冗余机械臂末端执行器的初始广义位置x0和终止广义位置xf（如下所示）。同时，初始和终止的广义速度均为0。

通过式(15)和积分运算，可以得到冗余机械臂初始和终止的关节角（如下所示）。逆向运动学求解时间为0.26 s，计算效率较高。

进而，通过式(16)～(18)，可以计算出冗余机械臂末端执行器从初始状态运动到终止状态各关节角的变化，如图3～图5 所示。整个仿真时间持续7 s。

图3 关节角变化曲线

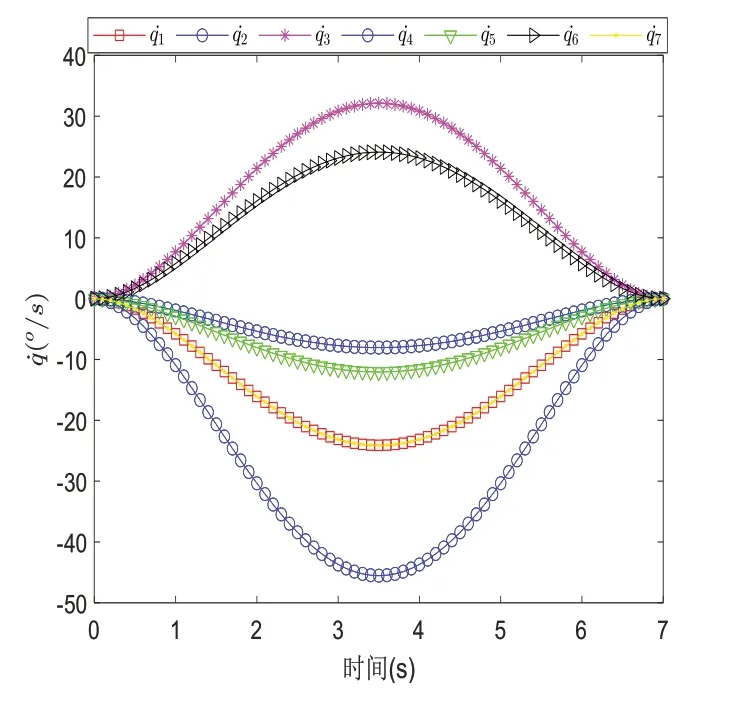
图4 关节角速度变化曲线

图5 关节角加速度变化曲线

为了进一步描述冗余机械臂在笛卡儿空间中的运动过程，本文借助Robotics Toolbox 建立了该机械臂的可视化模型，并给出了末端执行器的三维运动轨迹，如图6 所示。从图中可以看出末端执行器的变化趋势，三维运动轨迹较为光滑平坦，有利于优化关节控制力矩。

图6 关节角加速度变化曲线

最后，根据式(2)提取冗余机械臂末端执行器的位置变化序列和姿态变换序列，如图7和图8 所示。这里需要说明的是，本文将方向余弦表征的姿态矩阵转换成了欧拉角的形式。图中结果也证明了所提出的运动学方程的有效性，可以有效计算出冗余机械臂的运动状态。

图7 末端执行器位置变化曲线

图8 末端执行器姿态变化曲线

四、小结

本文提出了结合改进DH 参数法和加权最小二乘法的综合方法，来解决七自由度冗余机械臂的运动学建模问题，并采用五次多项式插值函数来计算其关节空间内的关节运动轨迹。仿真结果显示，改进DH 参数法可以很好地建立冗余机械臂正向运动学模型，并可以结合蒙特卡罗法得到机械臂的工作空间；加权最小二乘法可以快速计算出冗余机械臂的逆向运动学解，效率较高；五次多项式可以帮助机械臂快速规划出运动所需的关节运动轨迹，且关节运动较为平坦。

未来我们将进一步研究冗余机械臂运动学解析解法，并研究其动力学建模和运动控制。