Two-Stream Approximation to the Radiative Transfer Equation:A New Improvement and Comparative Accuracy with Existing Methods
2024-04-11MomoTEMGOUAAkanaNGUIMDOandNJOMO
F.Momo TEMGOUA,L.Akana NGUIMDO*,2,and D.NJOMO
1Environmental Energy Technologies Laboratory (EETL), Faculty of Sciences, University of Yaoundé,PO Box 812 Yaoundé, Cameroon
2Department of Electrical and Electronic Engineering,Faculty of Engineering and Technology,University of Buea,PO Box 63 Buea,Cameroon
ABSTRACT Mathematical modeling of the interaction between solar radiation and the Earth’s atmosphere is formalized by the radiative transfer equation (RTE),whose resolution calls for two-stream approximations among other methods.This paper proposes a new two-stream approximation of the RTE with the development of the phase function and the intensity into a third-order series of Legendre polynomials.This new approach,which adds one more term in the expression of the intensity and the phase function,allows in the conditions of a plane parallel atmosphere a new mathematical formulation of γ parameters.It is then compared to the Eddington,Hemispheric Constant,Quadrature,Combined Delta Function and Modified Eddington,and second-order approximation methods with reference to the Discrete Ordinate (Disort) method(δ-128 streams),considered as the most precise.This work also determines the conversion function of the proposed New Method using the fundamental definition of two-stream approximation (F-TSA) developed in a previous work.Notably,New Method has generally better precision compared to the second-order approximation and Hemispheric Constant methods.Compared to the Quadrature and Eddington methods,New Method shows very good precision for wide domains of the zenith angle µ0,but tends to deviate from the Disort method with the zenith angle,especially for high values of optical thickness.In spite of this divergence in reflectance for high values of optical thickness,very strong correlation with the Disort method (R ≈1) was obtained for most cases of optical thickness in this study.An analysis of the Legendre polynomial series for simple functions shows that the high precision is due to the fact that the approximated functions ameliorate the accuracy when the order of approximation increases,although it has been proven that there is a limit order depending on the function from which the precision is lost.This observation indicates that increasing the order of approximation of the phase function of the RTE leads to a better precision in flux calculations.However,this approach may be limited to a certain order that has not been studied in this paper.
Key words: Radiative Transfer Equation,two-stream method,Legendre polynomial,optical thickness,moments of specific intensity,conversion function,transmittance,reflectance
1.Introduction
Solar radiation interacts with the Earth’s atmosphere through absorption and scattering of the incident radiation as well as atmospheric thermal emission.The mathematical modeling of these interactions leads to an integro-differential equation called the Radiative Transfer Equation (RTE),whose resolution makes it possible to determine the reflected and transmitted fluxes essential for the calculation of the local heating/cooling rate and atmospheric reflectance and transmittance.Several approaches to the analytical resolution of the RTE have emerged in this sense,with more or less similar solutions that not only are easy to interpret but offer the most efficient representation of the real physical processes that take place in the transfer milieu.Some of the well-known ones include Spherical Harmonics,Matrix Operator,Monte Carlo,Successive Order,Discrete Ordinates Method and Doubling.Based on the spatial and spectral considerations,the Spherical Harmonics,Matrix Operator,and Doubling methods have better proven accuracy in the standard procedures,although their implementation is heavy given the amount of data,and consequently computational time,required to run them (Laszlo et al.,2016).The 16-streams Discrete Ordinary Method (DOM) outputs are in excellent agreement with those obtained by the Spherical Harmonics,Matrix Operator,and Doubling methods,and wherever accurate methods take enough time to solve the RTE,it has been shown that the 2-,4-and 16-stream DOAM (Discrete Ordinates Adding Method) solver computational times are 0.86,1.09 and 4.34 s,respectively,for azimuthally averaged radiance (Shi et al.,2021).
Since the precision of DOM increases with the number of streams,one can hence consider solving the RTE with very high resolution 128-streams DOM for an accurate result.However,as the number of streams increases,the model become a computational burden and that is why most satellite data assimilation requiring a computationally fast and accurate radiative transfer model uses two-stream approximation.The two-stream method is generally used in these resolutions because it produces mathematical solutions to the RTE faster,while taking into account the variability of the medium and the complexity of the processes,hence saving computation time.Although this method is used for many applications (e.g.,industrial heat transfer,radiative heating,meteorology,combustion),the speed affects its precision.It is therefore imperative to better understand this approximation in view to its improvement because errors may become unacceptably large under certain optical conditions depending on the method chosen.In this respect,Meador and Weaver (1980) developed a unified description of existing two-stream methods,but these were all limited to the firstorder approximation.Joseph et al.(1976) proposed the twostream delta-scaling approximation to improve the accuracy of calculated irradiances under strongly forward scattering conditions.Harshvardhan et al.(1987) and Toon et al.(1989) applied the method for the determination of the heating/cooling rate in a multiple scattering atmosphere.King and Harshvardhan (1986),still in a multiple scattering scheme,compared the accuracy of diffuse radiative properties computed using two-stream methods for a constant asymmetry factor and varying optical thickness.They concluded that two-stream models are the simplest and most computationally efficient to implement in a numerical atmospheric model,but their accuracy is limited to certain domains of the space parameter.The case of Eddington approximation is slightly more accurate in thick optical depth regions,while successive order leads to larger error with absorbing media (Lu et al.,2009;Hou et al.,2010).These observations have motivated the development of other solvers as twostream Disort or spherical harmonics that better take into consideration the complexity of the transfer process.Hou et al.(2010) showed that two-stream Disort is more accurate than the two-stream successive order for the calculation of fluxes in absorbing media.In the same context,it was found that two-stream Disort and hence high-stream Disort approximation (4,8,16… streams) methods are more accurate for heating rate and flux calculation than Eddington under cloudy conditions (Lu et al.,2009).Also,Stamnes and Swanson(1980) proposed a new look at the discrete ordinate method suitable for radiative transfer calculation in an anisotropically scattering atmosphere,while Kylling et al.(1995) dealt with a two-stream algorithm method on the basis of a general purpose multi-stream discrete ordinate algorithm and used the method to compute radiative fluxes,their divergence,and their mean intensities (actinic fluxes) at any depth in the transfer medium.
It is the case,therefore,that due to its very high speed and its ability to adapt to all areas of atmospheric science while incorporating modifications that tend to improve its accuracy,the two-stream approximation has been able to resist the new so-called rigorous methods.Indeed,although more precise,these rigorous methods sometimes require large quantities of data,which make them inoperative (spherical harmonics,for instance),and when they are effective,their computation time according to the spectrum to be covered and the volume of the transfer medium may become abnormally long.For instance,Chen et al.(2021) showed that,in low to medium dust opacity scenarios,the calculation of the radiative flux or heating rate with two-stream approximation gives good agreement with the higher order multiflux results with maximum differences of less than 2 K/sol,which is an irrelevant error in temperature simulation fields and atmospheric circulation in regional and global dust storm conditions.Furthermore,two-stream approximation can be applied to reduce the number of calculations when the selection rules method is to be considered.For instance,infrared flux calculation for a 30-layer atmosphere in clear sky with the selection rule using thek-distribution method takes one seventh longer than when using a two-flux approximation under the same conditions (Gabriel et al.,2000).Similarly,it was showed that the linearization of the Quadrature method is two times faster than the linearization of the twostream Disort (LIDORT) method (Spurr and Natraj,2011).It is for these reasons,among others,that two-stream methods remain very useful today for the development of many climate models,including global climate models (Randles et al.,2013;Baek,2017).
This paper discusses the resolution of the RTE in a plane and homogeneous semi-transparent layer using mathematical applications such as Legendre polynomials,spherical harmonics,and Dirac functions.The two-stream methods considered here are Eddington’s method,the Hemispheric Constant method,Quadrature method,Combined Delta Function,a modified version of Eddington’s method (hereafter simply referred to as the Modified Method),and the secondorder approximation.The Disort (δ-128 streams) method,to which the reflectance and the transmittance of the medium are compared,is also discussed.Subsequently,we propose a new resolution based on the approximation of the phase function and the intensity into third-order Legendre polynomial series with one more term than the traditional Delta-Eddington approximation but different from the one proposed by Matagne (second-order approximation)(Matagne,2011).The reflectance and transmittance obtained from the New Method approximation are also compared with those of the methods cited above.Applying the fundamental definition proposed by Yin and Song (2022),conversion functions are finally derived for the New Approximation Method as well as the other methods used in this analysis.
The rest of the paper is structured as follows: Section 2 discusses the resolution of the RTE by the various existing methods listed above and the New Method proposed here,and describes the γ parameters and conversion function for each of the methods except the second-order approximation,which uses spherical harmonics for flux calculations.Section 3 presents the results of transmittances and reflectances for each method and compares them with reference to the Disort(δ-128 streams) method.Finally,a summary and conclusions are presented in section 4.
2.RTE for diffuse intensity
The RTE under its global form is written as (Raut,2008)
where Ω and Ω′are the scattering and incidence solid angles,respectively;Lλ(τ,Ω) and Lλ(τ,Ω′) are the radiation specific intensities or intensities along the solid anglesΩand Ω′,respectively;τ(z,λ) is the optical thickness of the layer along the directionz;L◦(λ,T) is the black body radiation intensity;ϕ(τ,λ,Ω,Ω′) is the phase function;and ωλis the single scattering albedo.
In the rest of the paper,we remove λ from the equations but consider that the radiation remains spectral for simplicity.
2.1.Two-stream approximation method
The two-stream method allows the intensity variation in two fronts to be established: the reflected intensity (upward),which is denoted L+(τ,θ,φ);and the transmitted one (downward),denoted L-(τ,θ,φ) (Jiménez-Aquino and Varela,2005).Considering the vertical component of the layer’s optical thickness,the upward and downward fluxes under the conditions of azimuthal symmetry are expressed as
with µ=cos(θ).
Equation (1) then leads to a system of two equations,one fortheupwarddiffuse flux()andtheother forthe downwarddiffuseflux ().Withinthelimits solarspectrum,these fluxes are given by
By developing the intensity and phase function in a series of Legendre polynomials and applying spherical harmonics properties,we obtain,according to the assumptions(discussed later) and specific to each approximation methods(Eddington’s method,Hemispheric Constant method,Quadrature method,New Method),a new formulation of equations [Eqs.(3) and (4)] given by (Meador and Weaver,1980)
where γ1,γ2,γ3and γ4are specific parameters to the twostream method;F0is the incident flux (at the upper limit of the medium);ω is the single scattering albedo;τ is the optical thickness;and µ0is the cosine of the zenith angle of the incidence direction.The different γ parameters can be expressed as in Yin and Song (2022).
2.2.Solving the two-equations system
The semi-transparent medium chosen here is a plane atmosphereirradiatedatthetopbydirectflux [ Fd-(0)=0]andlimited belowby a blacksurface[(τh)=0].The upward[(τ)] and downward[(τ)]fluxes from thesystem formed by Eqs.(5) and (6) are the same as the ones developed by Yin and Song (2022) [their Eqs.(42) to (49)] with the consideration thatFP0andFnsare set to be zero.
Knowing the flux,the reflectivity and the transmittance can now be calculated with the following formulae:
The development of Eq.(7) permits us to reduce the reflectivityRand the transmittanceTfrom the global fluxes as (Meador and Weaver,1980) :
By restricting to the non-absorbing atmosphere (conservative scattering) conditions in agreement with Meador and Weaver (1980),we have ω=1 and K=0 (γ1=γ2),andRandTbecome
2.3.Two-stream approximation methods and formulation of γ parameters
2.3.1.Eddington,Hemispheric Constant and Quadrature methods
These three older methods were developed with certain assumptions on the intensity.The intensity expressions used to develop these three methods are:
• For Eddington’s method,the intensity is expressed as
• For the Hemispheric Constant method,the expression is
• For the Quadrature method,the intensity is
All the intensity expressions are well defined in (Yin and Song,2022).
The γ parameters,the phase function,and the conversion function of each of these methods were developed by Yin and Song (2022) and are here summarized in Table 1 in section 2.3.4 of this paper.

Table 1.Summary of the γ parameters of the different two-stream approximation methods.
2.3.2.Combined Delta Function and Modified Method
Following Meador and Weaver (1980),the intensities and the phase function in this case are
Yin and Song (2022) used Eq.(16) and their twostream approximation definition (F-TSA) to determine the conversion function D(µ,µ0) of this approximation method as
Using Eq.(17) in the expression of γ1and γ2developed as in Yin and Song (2022) [their Eqs.(25) and (26)],we obtain the first two parameters:
The two other parameters,γ3and γ4,are expressed as
where β(µ0) is the backscattering phase function,which represents the full scattering phase function.
For parameters γ3and γ4,the β(µ0) used in this work is the one parameterized with the Henyey-Greenstein phase function (Barker and Li,1995),i.e.,
2.3.3.Second-order approximation (Matagne)
Matagne (2011) used Spherical Harmonics approximation in solving the RTE.Contrary to the other spherical harmonics approximations,the intensity is expressed here as the sum of the first three terms of Legendre decomposition,instead of the first two terms.A similar approach is applied for the phase function,and hence
where,Li(τ),pi(µ) and αiare the isotropic radiance,the Legendre polynomial,and the weight of the Legendre polynomial,respectively.iis an integer.
Using the orthogonality condition of the Legendre polynomials and the recurrence formula,defined respectively as
l is an integer.
Matagne obtained the following expressions for the isotropic intensity using the spherical harmonics approximation:
Since the fluxes expressed in terms of intensity are given as
the use of isotropic intensities allows the rewriting of these as functions of two unknown parameters,γ1andγ2(Matagne,2011) as follows:
Considering that there is no downward diffuse flux at the top of the layer [Fd-(0)=0] and that there is no upward diffuse flux at the bottom [Fd+(τh)=0],one can therefore solve the system of two equations and hence deduce the reflectance and the transmittance for the method.
2.3.4.Third-order approximation method (New Method)
The intensity is decomposed here into a third-order series of Legendre polynomials.Again,
Referring to Eqs.(15) and (16),we have the expression of the higher orders of cl(τ):
Furthermore,the decomposition of the Henyey-Greenstein phase function into a series of Legendre polynomials(Randles et al.,2013) gives
That is,
As the intensity is now decomposed as
definingJas the average radiative mean intensity (first moment of the radiative mean intensity),Has the average flux (second moment of the radiative mean intensity),Kas the radiative average pressure (third moment of mean intensity),andGas the fourth moment of mean intensity (Heng et al.,2014),we obtain the following expressions:
Using the Eddington approximation,which specifies that
whereMis the moment of the radiative mean intensity (M0the first moment,M1the second),one can obtain the relationship between the different moments in their global form.n is an integer.Using Eq.(35) yields the following expressions:
Taking this latest directional equation into Eqs.(33)and (34) and considering Eqs.(3) and (4),the RTE becomes:
One can verify the statement of the conservation of the energy,which is required for all two-stream approximations,by
For the determination of the conversion function of this approximation method,it was considered that D(µ,µ0) is expressed as a third-order decomposition of the Legendre polynomial function:
where c0,c1,c2,c3are the coefficients to be determined.
Knowing the explicit formulation of the approximation parameters (γ) for the method along with the shape of the phase function,Eq.(7) can be used in the case of γ1to obtain a system of three equations in D(µ,µ0) as follows:
Substituting D(µ,µ0) and integrating the equations yields a system of three equations with four unknown coefficients.Taking c2=t as a parameter,one can solve the system and express D(µ,µ0) as
Applying on Eq.(39) the conversion function conditions of Yin and Song (2022),one finally obtains c2=t=0.Hence,the expression of the conversion function for the New Method is
This approach applied to Eddington’s approximation with the decomposition of the Legendre polynomial limited to the second order yielded the conversion function obtained in Yin and Song (2022).
Table 1 summarizes all the γ parameters of the different methods described above with the corresponding phase function and conversion function.
3.Results and discussion
On the basis of the methods discussed above,the radiative properties of the gas layer vary with the values of the coefficients γ1,γ2,γ3and γ4.Represented below are the reflectance and transmittance profiles for each of these methods as functions of the zenith angle µ0as well as the relative difference that exists between each of these methods and the Disort method taken as reference Disort (δ-128 streams)method taken as reference.Reflectance and transmittance are represented for four values of the optical thickness (0.25,1,4 and 16),two values of the single scattering albedoω(0.8 and 1),and a single constant value of the asymmetry factor,g=0.75.The relative difference is also represented for the same values of the optical thickness τ and single scattering albedo ω.
3.1.Reflectance profile
Figures 1 and 2 describe the variations in reflectance for ω=1 and ω=0.8,respectively.In these plots,Eq.(9) is used for ω=1 and Eq.(11) for ω=0.8.These results generally show a decrease of the reflectance when the cosine of the incident angle µ0increases,due to the fact that the optical path of the radiation in the semi-transparent medium reduces when µ0increases.There is also a decrease of the reflectance when the single scattering albedo decreases.In fact,part of the radiation is absorbed in the layer in this case.It can be seen from Fig.1 that the new method and Disort(δ-128 streams) profiles are very close for small values of optical thickness.As τ increases,the shapes remain very similar,with a form change occurring almost at the same points for the two methods,although the difference to the reference increases for all the methods.
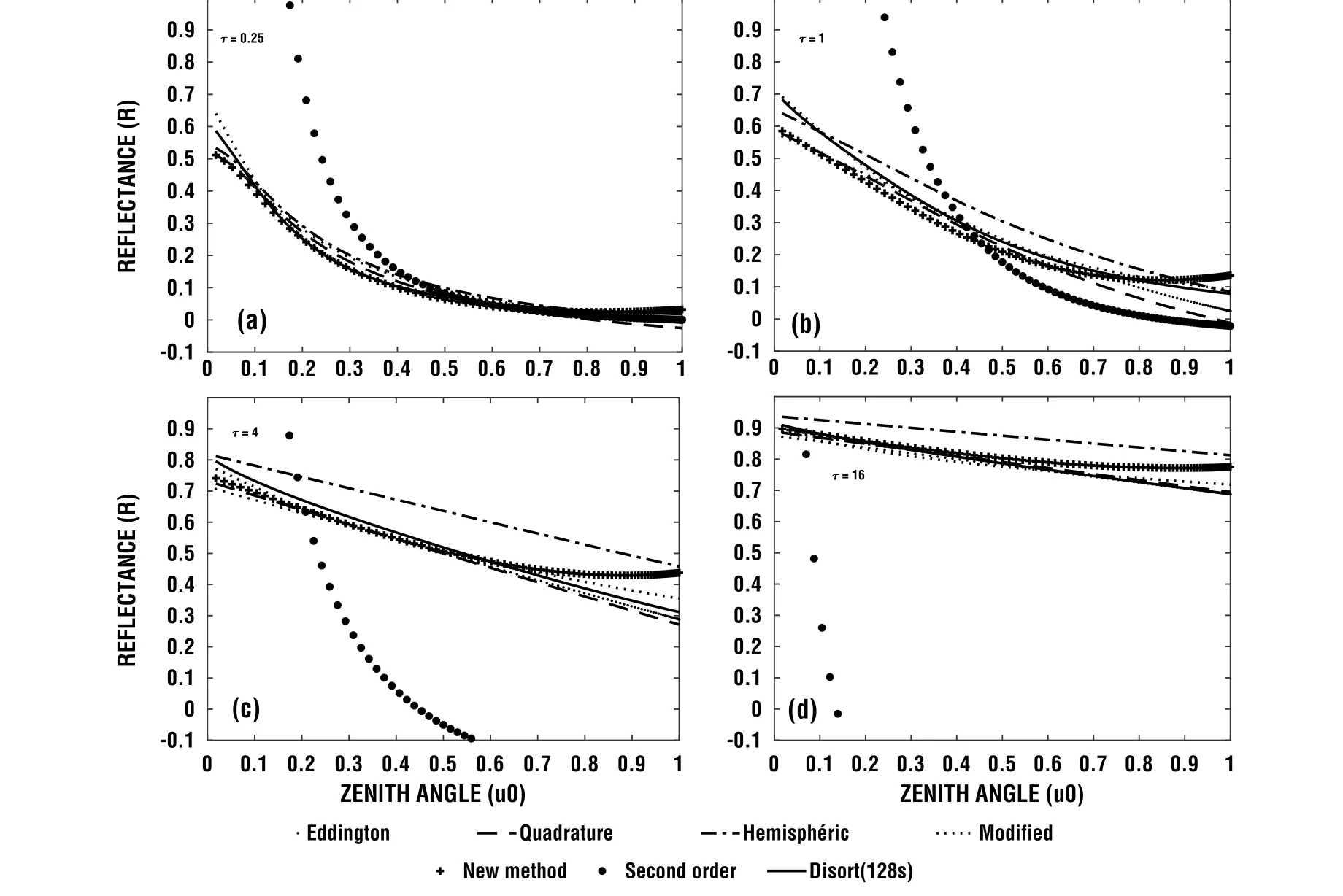
Fig.1.Profiles of the reflectance as a function of the incident angle and the optical thickness for all methods (ω=1).

Fig.2.Profiles of the reflectance as a function of the incident angle and the optical thickness for all methods (ω=0.8).
All the methods used in this analysis globally overestimate the reflectance,and the tendency increases with the optical thickness,except New Method,which generally underestimates the reflectance but remains very close to the Disort method,as much as Modified Method.However,consistent changes are noted with the different methods as the zenith angle µ0varies.It can be seen from Fig.1 that New Method is closer to Disort than Hemispheric Constant and secondorder methods in all cases.As compared to the Quadrature and Eddington methods,it is observed that for a non-absorbing atmosphere(ω=1),New Method is more accurate in the particular case of a thin atmosphere.In fact,the graph of New Method tends to move away from the reference as the optical thickness increases.However,the general trend of New Method is more comparable to Disort than any of the two approximation methods.On the other hand,New Method’s accuracy is comparable to that of Modified Method per interval of µ0(i.e.,µ0lying between 0.2 and 0.9 for Fig.1a,for instance) for a conservative scattering atmosphere,but becomes more significant as µ0increases for a less scattering atmosphere.Figure 2 confirms the better precision for New Method for all values of µ0.The particularity with this case (ω=0.8) is that the Quadrature and Eddington models move far away from the reference graph as the optical thickness of the slab increases.This observation may reinforce the idea that in real atmosphere New Method is more appropriate than any other two-stream method.
Figures 3 and 4 show the relative difference between the reference (Disort) and other methods (Eddington,Quadrature,Hemispheric Constant,Modified,second-order,and New Method).This quantity displays the different ways the methods overestimate or underestimate the reflectance in reference to Disort,and the analysis of the two graphs clearly confirms all the observations mentioned above.In fact,the highest correlation between New Method and Disort in nearly all the cases proves its accuracy.The precision of New Method accentuates when the single scattering albedo reduces,as can be seen in Fig.4.However,the precision tends to decrease when the optical thickness increases(Fig.3).

Fig.3.Relative reflectance difference with reference to the Disort (δ-128 streams) as a function of the incident angle and the optical thickness (ω=1).
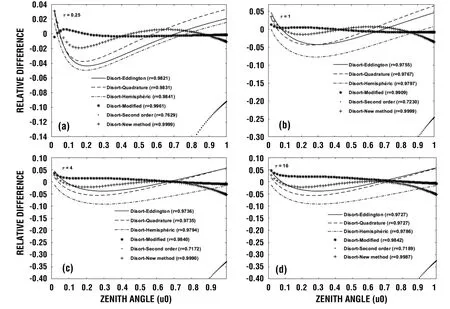
Fig.4.Relative reflectance difference from the Disort (δ-128 streams) method as function of the incident angle and the optical thickness (ω=0.8).
3.2.Transmittance profile
Figures 5 and 6 show the profiles of the transmittance as functions of the zenith angle µ0,as described by Eqs.(12)and (14).It can be seen that all methods generally overestimate the transmittance when ω=1,while it is underestimated for ω=0.8.Also,the transmittance increases with zenith angle and reduces when the single scattering albedo decreases.In addition,the transmittance reduces when the optical thickness increases,a behaviour which is expected since the increase of the optical thickness implies more gas,aerosol or cloud,which can reduce the radiation by scattering or absorbing.Figure 5 shows that,relative to Disort,New Method is less precise,with µ0ranging from 0.05 to 0.65,and more accurate for µ0greater than 0.65.This feature is normal since when the single scattering albedo is equal to 1 the transmittance is just the complement of the reflectance and,as such,all the observations made in the context of Fig.1 will be the opposite of the ones on Fig.5.In turn,the high degree of accuracy of New Method is noticeable in Fig.6 since it overestimates less than any of the other methods for all values of µ0and even when the optical thickness increases.For the lowest value of the optical thickness(τ=0.25),the transmittance tends to 1 when the sun is at the zenith.This observation,in perfect agreement with Meador and Weaver (1980),is explained once again by the decrease of the optical path as the sun rises in the sky.In fact,an optically thin atmosphere naturally transmits radiations more than a thick one.
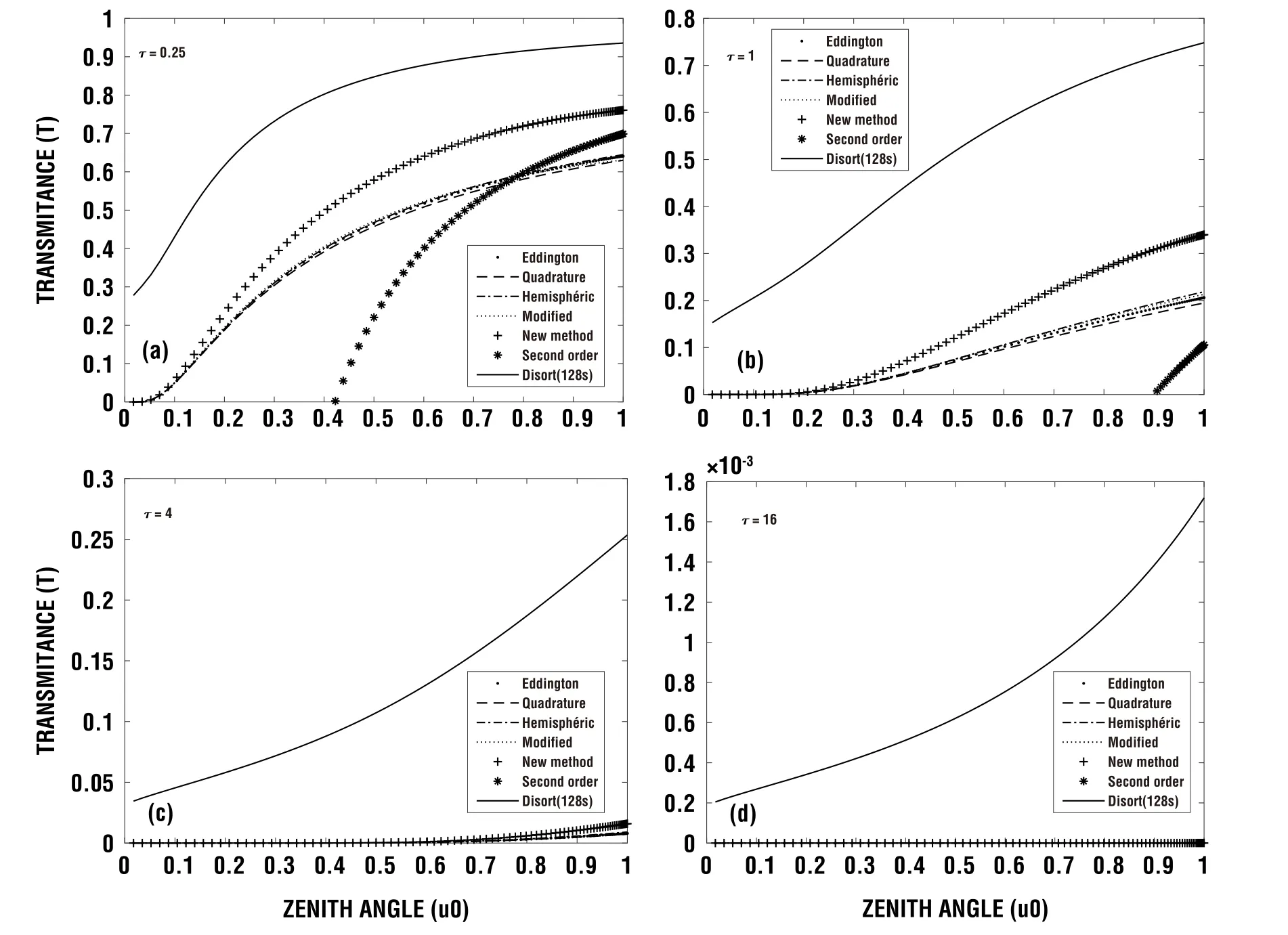
Fig.6.Profiles of the transmittance as a function of the incident angle and the optical thickness (ω=0.8).
The observations made with Figs.5 and 6 can be confirmed with Figs.7 and 8,which display the relative difference between Disort (δ-128 streams) and the other methods.Although the correlations with Disort are high for nearly all the methods,it can be seen that when ω=1,the transmittance and reflectance display similar correlations (Fig.3 and 7).In the same condition,New Method’s precision increases with the optical thickness (Fig.7),confirming the relationship between the transmittance and the reflectance for a conservative scattering atmosphere.Furthermore,in real atmosphere(Fig.8),the relative difference with New Method is closer to zero compared to any other method used in this analysis.This feature,which is observed for all cases of optical thickness,proves once more the high precision of New Method and confirms its ability to adapt to variable atmospheric conditions.

Fig.8.Relative transmittance difference from the Quadrature method as a function of the incident angle and the optical thickness (ω=0.8).

Fig.9.Profile of the exponential function and the corresponding first-,second-and third-order Legendre polynomial expansions.

Fig.10.Profile of the function g(x)= and the corresponding first-,second-and third-order Legendre polynomial expansions.
New Method was developed in this work in order to improve two-stream approximation methods and its high degree of accuracy for large domains of the zenith angleµ0has been proven.This could mean that when a function is developed into a series of Legendre polynomials,the precision improves as the order of the series increases.To verify and understand this concept,two functionsf(x) andg(x)have been developed to first,second and third order of the Legendre polynomial.The two functions,which are continuous between-1 and 1,are f(x)=exp(x) and
Below are the different expressions of said functions under their Legendre polynomial forms:
Figures 9 and 10 represent the functionf(x) andg(x),respectively,forxtaking values between 0 and 1.It can be seen that the precision of the corresponding Legendre polynomials increases with the order of approximation and generally for the values where New Method is more accurate than the others.This observation proves that third-order approximation shows better accuracy than first and second orders.However,this conclusion needs to be carefully verified,since for more than third-order approximation there is no evidence if the trend of the function and its precision will still hold or the function will oscillate.In fact,for f(x)=exp(x),it was shown by Laroche (2003) that the function starts oscillating from n=8.
4.Conclusion
This work has revisited five two-stream approximation methods (Eddington,Hemispheric Constant,Quadrature,Modified,and second-order approximation),one multi method (Disort),and proposed New Method for the resolution of the RTE.A comparison of these methods was made with reference to the rigorous Disort (δ-128 streams) method.The results obtained show generally expected trends,including the decrease in reflectance and the increase in transmittance with the cosine of the solar zenith angle.Likewise,the reflectance increases while in general the transmittance decreases with optical thickness.It also emerged that New Method offers better accuracy compared to the other methods.In fact,linear correlation analysis shows that New Method generally correlates more with Disort than the other methods.However,this high precision does not cover the whole range of zenith angle µ0.Furthermore,it has been proven with the exponential function that there is an order of Legendre polynomial expansion from which the approximated function oscillates around the original function.Hence,it would be interesting to investigate the precision of New Method with increasing (n>3) order of the polynomial and when γ3uses the full scattering phase function.
Acknowledgements.The authors are grateful to Dr Istvan LASZLO of the Department of Atmospheric and Oceanic Sciences/University of Maryland (USA) for his help for a better understanding of the Disort (δ-128 streams) method used as the benchmark in this work.
杂志排行
Advances in Atmospheric Sciences的其它文章
- Record-breaking High-temperature Outlook for 2023: An Assessment Based on the China Global Merged Temperature (CMST) Dataset
- Impact of Sky Conditions on Net Ecosystem Productivity over a “Floating Blanket” Wetland in Southwest China
- Circulation Pattern Controls of Summer Temperature Anomalies in Southern Africa
- Attribution of Biases of Interhemispheric Temperature Contrast in CMIP6 Models
- The Spatiotemporal Distribution Characteristics of Cloud Types and Phases in the Arctic Based on CloudSat and CALIPSO Cloud Classification Products
- Impacts of Ice-Ocean Stress on the Subpolar Southern Ocean:Role of the Ocean Surface Current
