基于突变理论的泥岩隧道稳定性及极限位移确定

2024-04-10曹明星严松宏杜嘉轩

兰州交通大学学报 2024年1期

曹明星,严松宏,杜嘉轩

(兰州交通大学土木工程学院,兰州 730070)

软岩隧道破坏失稳在工程中频繁出现,其变化速率快,应力应变间关系复杂。在土木工程各个方面都已有应用的例子,尤其在研究岩土体的稳定性中应用较多[1-4]。李照众等[5]应用模糊数学理论研究了煤矿开采面的稳定性及预测预报动力现象的准确性,经现场验证,该方法是可行的。文献[6-7]以岩石材料破坏准则为基础,通过能量原理,分析了围岩系统应变能破坏规则,计算了岩石的内部能量公式,得出了尖点突变模型的判别表达式,并且结合有限元程序,把破坏准则引入程序设计中进行计算。周平等[8]对昔格达地层的隧道岩体进行了试验,得出了含水率对隧道围岩稳定性的影响程度,通过应用突变理论来分析隧道围岩稳定性。宋瑞刚等[9]研究了断层破碎带隧道围岩的稳定性,通过建立断层破碎带隧道围岩的突变理论模型,推导了基于尖点突变模型的破碎带梯度方程,验证了其可行性。王心飞等[10]对深埋隧道软弱围岩塌方进行了力学模型的建立,分析了水对围岩稳定性的影响。

1 依托工程概况

某隧道为牡绥铁路的一条控制性工程,最大埋深约140 m。隧道围岩破碎,遇水容易变软,容易涌泥、流砂和塌方。接触带起伏大,局部形成储水构造,使得隧道施工难度大,风险高,进度异常缓慢。

2 隧道围岩稳定性分析

2.1 尖点突变模型

突变理论首先由有些学者提出[11],它利用数学方法研究了非静止系统中状态发生突变的一些原理,从分叉理论开始[12-13],其尖点突变模型如图1所示。

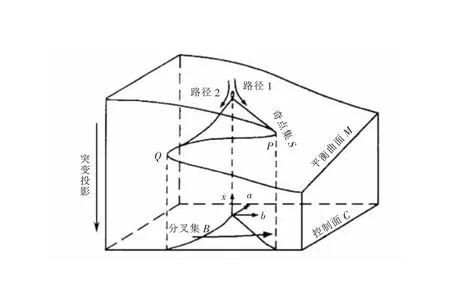
图1 尖点突变模型示意图

2.2 软弱围岩突变分析

隧道开挖打破了原始的应力平衡状态,开挖后围岩应力重分布,软弱围岩加速了塑性区的变化,极速变化很可能导致围岩失稳发生塌方。根据隧道所处的实际状况,建立以下力学模型[14-17]如图2所示。

图2 软弱围岩失稳力学模型

破碎围岩为H1,围岩重为mg,层理角度为α,隧道轮廓为H,隧道掘进后围岩变形为u,塑性区为Rp,弹性区半径为Re。弹性介质应力应变关系为

(1)

τ1=τm(u>ue)

(2)

式中:τ1为弹性区剪应力,τm为弹性区残余抗剪强度,ue为最大剪应力位移,G1为剪切模量。

塑性区应力应变关系为:

(3)

式中:τm为塑性区剪切强度初值,τ2为塑性区剪应力。

软弱围岩隧道的总势能函数为:

(4)

式中:S1为弹性范围位移,S2为塑性范围位移。

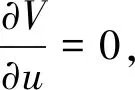
(5)

(6)

由mgsinα=0

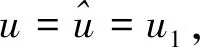
对(5)式用泰勒公式展开,将平衡曲面转化为

(7)

将(7)式作变换代换得到突变理论的标准形式曲面为

V′(x)=x3+μx+ν

(8)

式中:

(9)

μ=3(k-1);ν=3(1+k-Ψ)

(10)

式中:x为状态变量,μ、ν为控制变量,k为刚度比,Ψ为几何力学参数。

围岩发生失稳的条件是分叉集方程,即

Δ=4μ3+27ν2=0

(11)

把(10)带入(11)得

4(k-1)3+9(1+k-Ψ)2=0

(12)

可以看出只有当μ≤0时,才会失稳,得到围岩失稳的条件为

(13)

2.3 软弱围岩失稳分析

在隧道掌子面推进过程中,用隧道拱顶竖向变形S为状态变量,位移时间函数关系为:

S=f(t)

(14)

用泰勒级数展开(14)式

(15)

取前5项,得到:

(16)

(16)式变为

(17)

对应关系为:

(18)

对(18)式作变换,推导出围岩稳定表达式为

(19)

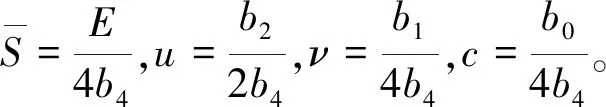
由尖点突变理论可知,软弱围岩稳定判别为:Δ=4μ3+27ν2,Δ≤0,围岩失稳,Δ>0,围岩稳定。

3 隧道极限位移确定

隧道开挖过程主要是岩体应力释放过程[18],隧道开挖中,当隧道发生变形时未能准确的评价隧道的目前状况,但是可以通过评价隧道岩体塑性的状态来判断隧道稳定性[19]。在隧道施工过程中,隧道围岩应力发生变化,围岩之间相互作用变差,一些围岩处于塑性状态,随着开挖步序的进行,塑性区变大,围岩逐渐发生屈服。隧道轮廓边的岩体破坏变大,随着塑性的增加,一些岩体变为流塑性,出现突变,进而引起围岩变形增大,围岩失稳[20]。因此,可以改变隧道围岩应力所占百分比,找出隧道塑性的变化,从而确定位移最大值[21],和支护发生失稳破坏[22]。应用突变理论对隧道围岩进行分析,采用数值模拟对隧道进行极限位移分析,确定出隧道极限位移,对隧道二次衬砌支护时机有一定作用。

在有限元计算的过程中,对隧道进行分部开挖,找出塑性应变最大值,得到随着应力的释放过程中塑性应变速度和加速度,找到其突变点,最后确定出最大位移[23-25]。

4 隧道极限位移数值模拟

4.1 有限元模型的建立

采用有限元软件进行建模,原始应力状态仅有自重应力,围岩采用摩尔库伦本构模型,由弹性力学可知,在隧道施工过程中,5倍洞径以外岩体影响因素较小,因此隧道数值模拟过程中,隧道两边范围土体都是50 m,根据隧道埋深,在上边界需加50 m土体所产生的压力,开挖方法如图3所示。将每部开挖时塑性应变发生最大处的塑性应变值逐一提取,求出塑性应变随应力释放率变化的速度和加速度,然后绘出塑性应变、塑性应变速度和加速度随应力释放率的变化曲线,找出加速度曲线中的突变点,最后根据塑性应变加速度的突变点找出毛洞开挖后的极限位移。

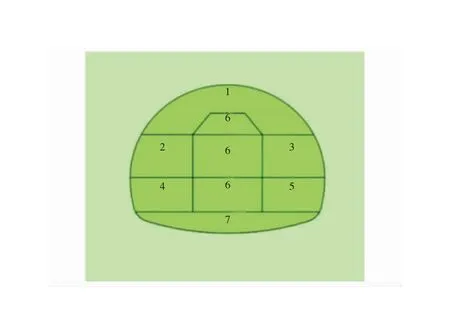
图3 开挖步序示意图

首先开挖第一步,进行计算,根据第一步开挖时的应力释放开挖第一步,然后进行衬砌支护,按照这样的步骤进行循环开挖,从上一步开挖的极限位移确定释放率。数值模拟力学参如表1所列。

表1 模型力学参数

喷射混凝土截面:方形,B=1 m,H=0.3 m。应用等效原理对弹模进行计算,折算后弹模为30.25 MPa。

4.2 有限元模拟分析

模拟隧道每开挖一步后设置应力释放系数,开挖步序及各节点释放如图4所示。

图4 隧道开挖步序

4.2.1 工况1

如图4(a)所示为隧道第一部开挖横断面图。根据隧道变形可知,拱顶作为监测点,所以找到拱顶的节点和拱腰节点进行分析,首次开挖时,围岩应力释放为5%进行计算,监测点变化曲线如图5所示,可以看出释放率为75%时,塑性应变加速度在0.7时发生了转折,如图6所示,可以看出此时的位移值,拱腰水平收敛值为1.4 cm,拱顶竖直位移是17.06 cm。

图5 拱顶塑性应变、速度、加速度随应力释放率变化

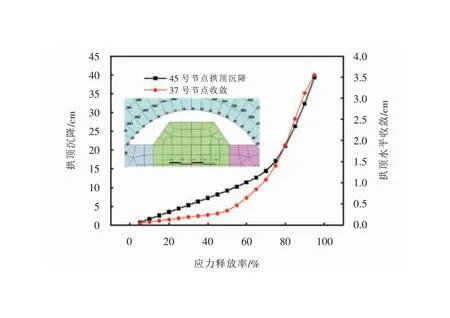
图6 位移随应力释放率变化

4.2.2 工况2

如图4(b)所示,为隧道第二部开挖横断面图,如图7所示,随应力释放的塑性变形曲线。可以看出1 532号节点在应力释放为75%时,塑性应变出现转折点,根据突变理论,此点为突变点。如图8所示, 45号节点和27号节点随应力释放位移的变化情况。首先把第一部开挖围岩的释放率设置为75%,支护释放20%,然后开挖第二部进行计算,释放设置为5%。

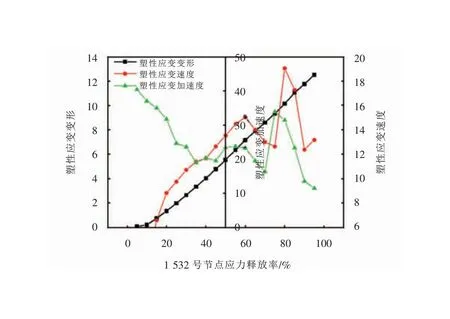
图7 1 532号节点塑性应变、速度、加速度随应力释放率变化

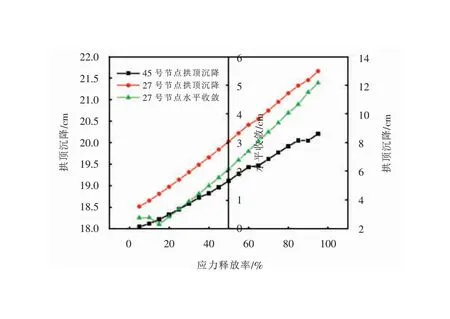
图8 位移随应力释放率的变化曲线

4.2.3 工况3

隧道开挖第三部时,首先把第二部开挖时围岩承担75%,支护承担20%,下一步释放5%,第三部隧道应力释放也是5%。监测点选为45、27、103和6号节,如图4(c)所示。分别提取沉降、水平位移及6号节点的塑性应变。

6号节点的塑性应变、速度和加速度曲线如图9所示[26],应力释放率为65%时加速度出现了突变点,拱顶的沉降为24.77 cm,拱脚的沉降为12.61 cm、水平收敛为6.99 cm、最大跨水平收敛为10.32 cm。拱顶、拱脚及最大跨位移曲线如图10所示。

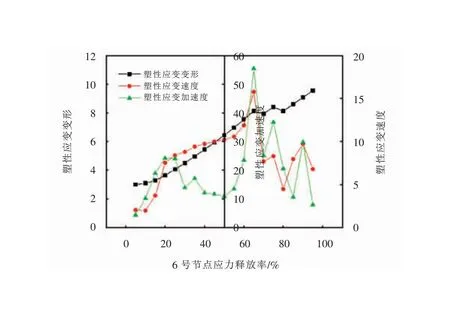
图9 6号节点塑性应变随应力释放率变化

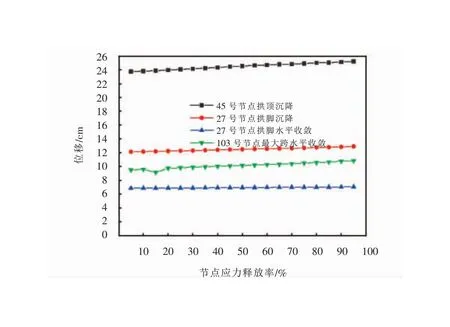
图10 第三部开挖后位移随应力释放率的变化曲线

4.2.4 工况4

如图4(d)所示,为隧道第四部开挖横断面图,如图11所示,随着释放率塑性的变化情况,释放率达到60%时塑性加速度出现了突变点,得到极限位移对应的释放率为60%。隧道第四部开挖,所选位移监测点如前三部,其位移变化曲线如图12所示。首先应把前一部所开挖的岩土体进行设置,围岩释放65%,支护释放30%,进行计算第四部。

图11 105号节点塑性应变随应力释放率变化

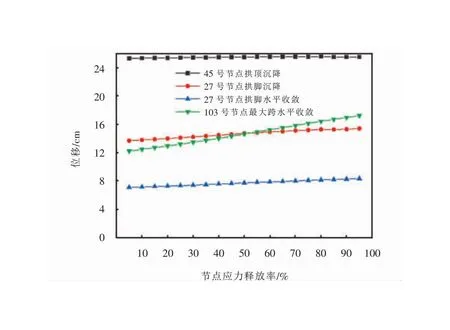
图12 第四部开挖后位移随应力释放率变化曲线

如图12所示,拱顶的沉降为25.52 cm,拱脚的沉降为14.93 cm、水平收敛为7.88 cm、最大跨水平收敛为15.23 cm。

4.2.5 工况5

隧道开挖第五步时,首先把第四部开挖时围岩承担60%,支护承担35%,下一阶段释放5%。监测点选为45、27、103和120号节点进行分析,如图4(e)所示。分别提取沉降、水平位移和应变值,如图13所示。应力释放率达到50%时加速度出现了突变点,可得到应力释放率达到50%时的位移为此次开挖的极限位移。拱顶的沉降为25.87 cm,拱脚的沉降为16.52 cm、水平收敛为8.88 cm、最大跨水平收敛为18.95 cm。如图14所示为拱顶、拱脚处和最大跨位移曲线图。

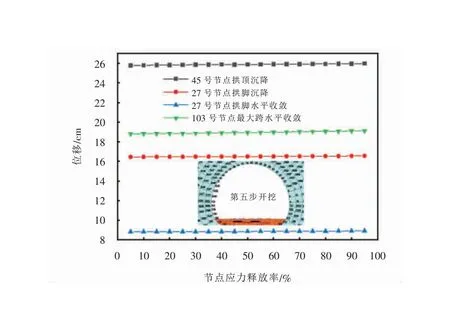
图14 位移随应力释放率的变化曲线

4.2.6 工况6

隧道开挖第六步时,先把第五步开挖时围岩承担50%,支护承担45%,下一阶段释放5%。开挖时,监测点选为45、27、103和203,如图4(f)所示。203号节点塑性应变、速度和加速度曲线,如图15所示。可以看出,应力释放率为45%时加速度出现了突变点,此时拱顶的沉降为25.93 cm,拱脚的沉降为18.82 cm、水平收敛为10.33 cm、最大跨水平收敛为23.62 cm。拱顶、拱脚和最大跨位移曲线如图16所示。