考虑工艺约束的多阶耦合集成调度问题优化
2024-04-10苏章圣
苏章圣,邓 超+,钱 斌,胡 蓉,陈 波
(1.昆明理工大学 机电工程学院,云南 昆明 650500;2.昆明理工大学 信息与自动化学院,云南 昆明 650500;3. 云南省烟草公司红河州公司,云南,红河 652300)
0 引言
在国家全面推进制造业生产过程智能化战略背景下,混合生产作为众多制造企业实现柔性生产的一种主流方式,常用于工艺具有相似性产品的生产中,在发动机、汽车、家电等行业中应用极为广泛。如何从调度的角度提升其混合系统智能化水平成为近年来制造领域研究热点之一,备受工业界关注。
对于现有混合生产系统的调度研究,随着调度理论的丰富与信息技术手段的增强,从只考虑产品混流装配的单系统调度问题向加工到装配整个流程的复杂系统转移。王炳刚等[1-2]分别研究了加工阶段为一条柔性线,装配阶段为带缓冲区的多并行机流水线和一条混合装配线的加工-混装两阶段调度问题,以平顺化混合装配线的部件消耗和最小化加工线总切换时间为优化目标,提出了多目标算法用于求解问题。随后,李修琳等[3]在文献[2]基础上进一步研究了装配阶段考虑部件装配和产品总装过程的加工-混装两阶段调度问题,以最小化在制品成本为目标,设计集成模拟退火混合遗传算法求解问题。然而,随着交通运输业快速发展,企业跨区域建厂成为主流,加工-混装过程中的运输环节不容忽视。文献[4-6]虽然将运输阶段考虑到加工-装配两阶段问题中,但却将运输过程简化为常数。邓超等[7]考虑了运输阶段车辆载重约束和工件分批运输问题,将车间调度与运输调度集成,把问题扩展为带批量运输的加工-运输-装配三阶段集成调度问题,以最小化最大完工时间为优化目标,设计融合规则的混合分布估计算法进行优化求解,但却将装配阶段简化为单机调度问题,并未考虑产品在装配时多工艺约束和多机装配的混装问题。KOMAKI等[8]对混装问题进行详细的分类和综述,认为大多数研究将产品结构设置过于简单,只为每个产品考虑一个装配操作,这与现混合装配企业生产中产品结构多样、存在多个装配工序的情况并不相符。因此,进一步研究考虑工艺约束的多阶段集成调度问题具有重要的应用价值。该问题需要同时考虑多层级物料清单(Bill of Materials with Multi -Level,BOM_ML)结构中所有零部件的加工工序、运输和装配工序调度,具有生产过程阶段间耦合约束多、各阶段间关联性强的特点,是一类典型多阶耦合约束(Multi-stage Coupling Constraints,MCC)优 化 问 题。目前,已有学者将多阶耦合性运用到求解装配作业车间调度问题并取得了良好效果[9-10]。由此,进一步探索结合耦合性的多阶段集成调度问题(Multi-stage Coupling Integrated Scheduling Problem with Process Constraints,MCISP_PC)的高效求解方法具有重要理论意义。
复杂系统集成调度问题的求解难度较大,在运用算法对其求解的过程中,融入启发式规则或多种操作机制(策略)于改进型算法中是目前较为有效的处理方式。譬如在群优化算法中,YAVARI等[11]针对包含m次加工和1次装配的集成调度问题,以最大化两阶段装配系统的利润为优化目标,结合先进先出规则(First In First Out,FIFO)分配机器,引入半置换(Semi-Permutation,SP)机制划分种群,对遗传算法进行改进,从而提出半置换遗传算法(SP Genetic Algorithm,SPGA)对问题进行求解。ZHENG等[12]针对加工-运输-装配的集成调度问题, 以最小化最大完工时间为目标,运用FIFO规则分配机器,提出结合种群分类机制、高斯学习策略和精英学习策略的改进混合蝙蝠算法(Improved Hybrid Bat Algorithm,IHBA)对问题进行求解。在学习型算法中,ZHANG等[13]对分布估计算法(Estimation of Distribution Algorithm,EDA)的概率学习模型进行改进,针对分布式装配置换流水车间调度问题,将概率学习模型拓展至三维并结合多种变邻域操作和加速策略,利用最短加工时间优先规则(Shortest Processing Time,SPT)为工件分配工厂,从而完成复杂系统求解。郭晨等[14]则对EDA的局部搜索作进一步细化,针对不确定环境下的分布式加工-装配调度问题,以最小化拖延期为优化目标,提出基于多维编码的混合差分搜索及变邻域的混合EDA,设计基于概率模型相似度的变异策略动态选择搜索策略,提高算法的局部勘探能力。也有学者采用结合问题性质,提出相关规则与算法结合的处理方式。JOO等[15]针对加工-运输两阶段集成问题,对不同子问题设计相关求解规则,在遗传算法框架下进行仿真实验以确定最佳规则组合,并利用最优规则组形成元启发框架对优质解进行搜索。WANG等[16]针对两阶段混合装配问题,对问题结构性质进行分析,提出了10种不同情况下的优势规则(Dominance Rule,DR)并进行了证明,结合反向粒子群算法(Opposition-based Particle Swarm Optimization algorithm,OPSO)形成DR_OPSO算法来对优质解进行搜索。上述文献表明,现有研究中结合问题性质设计有效的启发式规则与算法结合可提升求解效率,但在算法层面仍将问题本身和求解算法之间剥离开来,把精力集中在提升算法本身的性能上,缺少从分析问题特性的角度出发设计行之有效的算法操作,导致求解效果在问题求解难度不断增大时显得收效甚微。因此,在面对复杂系统集成调度问题上,不仅需要结合问题特性的设计有效启发式规则,还需考虑到算法全局和局部搜索与问题本身的关联性,从而探索融入问题特性的高效求解方法是目前需进一步解决的问题。
综上,结合问题多阶耦合性,本文提出一种结合规则启发式的混合分布估计算法(Hybrid Estimation of Distribution Algorithm with Rule Heuristics,HEDA_RH)求解以最小化最大完工时间(Makespan)为优化目标的MCISP_PC。先分阶段构建问题排列模型,在分析问题耦合特性的基础上,采用只针对加工阶段的编码,后续阶段通过设计基于问题性质的求解规则完成问题解码。并设计HEDA_RH求解MCISP_PC。在HEDA_RH中,依据个体中发现的两种块结构特征,结合问题耦合性质,从全局角度设计两种采样机制以提升解的搜索效率;从局部角度设计矩阵立方学习模型,通过积累6种启发式搜索操作的优质信息,自适应地调整搜索深度及选择搜索操作。
1 问题描述及数学模型
1.1 问题描述
MCISP_PC描述如下:根据订单和产品多层级物料清单,组成产品的零件加工所需原材料由不同供应商提供,再分别于加工阶段完成多工序加工,后经运输阶段运送至混装阶段完成产品装配。加工阶段中,零件根据加工工艺路线在M台异构并行机完成所有工序则视为加工完成。运输阶段中,零件由T辆载重为Gmax的同型运输车分批运送到混装阶段。混装阶段中,根据产品零件组成和装配工艺约束在K台装配机器上完成装配,从而完成整个生产。问题模型如图1所示,产品多层级物料清单如图2所示,不同产品间存在相同零件和装配工序。此外,若需了解MCISP_PC的详细流程或实例,请参见附录中的问题实例。

图1 MCISP_PC示意图
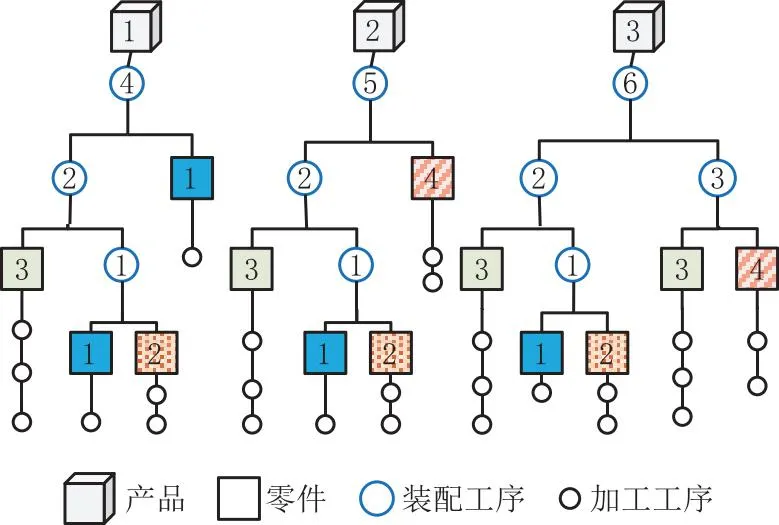
图2 产品多层级物料清单
MCISP_PC中,零件在加工阶段考虑释放时间和不同型号零件间在机器上加工时的设置时间;运输阶段考虑分批运输、车辆载重和运输速度;装配阶段考虑产品零件组成和装配工艺约束。问题中的假设如下:
(1)不同产品间可存在相同的零件;
(2)同种加工工序在某零件加工中至多为1次;
(3)同种装配工序在某产品中至多为1次;
(4)加工工序、零件运输和产品装配工序一旦开始不可被中断;
(5)加工机器与装配机器某一时刻至多能处理一个工序,运输车辆某一时刻至多运输总重不超过车辆最大载重。
1.2 问题数学模型
文中涉及到的符号说明如下:
z为产品下标,z∈{1,2,…,P},P为产品种数;
q为零件下标,q∈{1,2,…,Q},Q为零件种数;
o为加工工序下标,o∈{1,2,…,O},O为加工工序种数;
a为装配工序下标,a∈{1,2,…,A},A为装配工序种数;
m为加工机器下标,m∈{1,2,…,M},M为加工机器数;
t为运输车辆下标,t∈{1,2,…,T},T为运输车辆数;
k为装配机器下标,k∈{1,2,…,K},K为装配机器数;
Dz为产品z的需求量,Dq为零件q的需求量;
dP-A为加工阶段到装配阶段的运输距离;
Rq为零件q的原材料到达(释放)时间;
Tom为工序o在机器m上的加工时间;
Tak为装配工序a在机器k上的装配时间;
Tq,q′为零件q与q′间的设置时间;
Gmax为车辆最大载重;
V0为车辆空载时的速度;
jqr为第r个零件q,r∈{1,2,…,Dq};
pzh为第h个产品z,h∈{1,2,…,Dz};
nq为零件q的加工工序数;
nz为产品z的装配工序数;
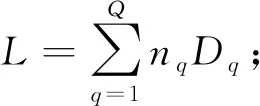

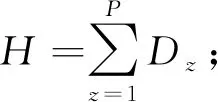

Um为机器m上的加工工序总数;
Ut为车辆t的运输总趟数;
Uk为装配k机器上的装配工序总数;
Gtw为车辆t第w趟运输的重量,w={1,2,…,Ut};
Vtw为车辆t第w趟运输的速度,w={1,2,…,Ut};

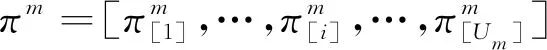

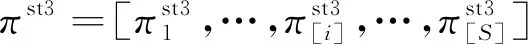
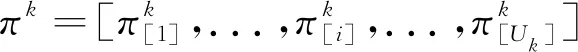


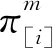

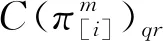

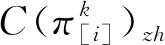

1.2.1 加工阶段

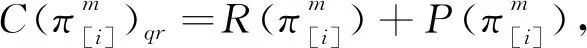
(1)
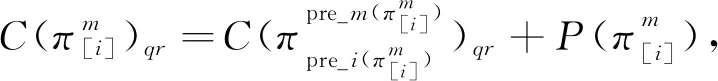
(2)
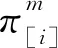
(3)

(4)
1.2.2 运输阶段
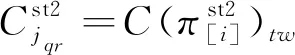
(5)
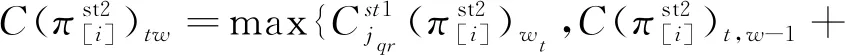
(6)
1.2.3 混装阶段
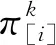
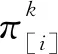
(7)
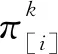
(8)
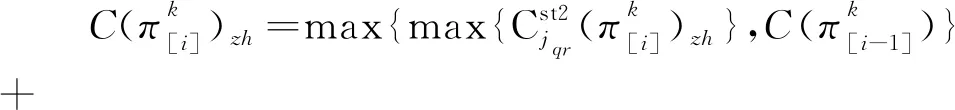
(9)
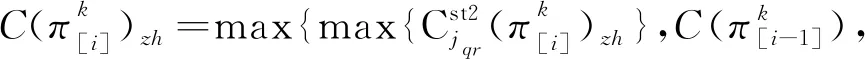
(10)
1.2.4 优化目标
式(11) 定义Makespan(Cmax(π))为最后一个装配产品的完工时间,优化目标为在加工、运输、装配3个阶段的排序π=[πst1,πst2,πst3]中找到最佳排序π*使得式(12)中三阶段的总完工时间Makespan(Cmax(π))最小。
(11)
(12)
2 MCISP_PC多阶耦合性分析
MCISP_PC是将加工、运输和装配一同处理的车间与运输集成的多阶段调度问题。具有生产过程阶段间耦合约束层阶性、约束时序性和关联性的特点,是一类典型的多阶耦合约束优化问题。
(1)耦合约束层阶性 MCISP_PC涉及到产品的多级物料清单、零件加工工序约束及产品装配工艺约束。产品的装配需要满足所组成的零件都到达,零件能被运输需要满足该零件所有工序都加工完成,层层递进,各层级之间联系紧密,这是实现耦合的前提。
(2)耦合约束时序性 各阶段间在生产运输过程中存在互为因果的关系,且具有伴生性。产品装配开始时间受限于所需零件的运达混装厂的时间;运输开始时间受限于零件的加工完成时间;加工阶段零件开始加工时间受限于工序释放时间。阶段间的发展关系并非静止状态,而是处于动态变化之中。耦合状态的形成过程就是各自阶段在时序列上不断交互衔接、前进的过程。

3 编码及解码规则设计
针对MCISP_PC,若对[πst1,πst2,πst3]3个阶段的序一一编码,将会由于解空间极为庞大而出现搜索效率低和收敛困难等问题。因此,结合MCISP_PC中存在的多阶耦合特性采用只针对加工阶段的编码,并基于各阶段耦合特征设计规则形成多个规则组完成后续阶段的解码。
3.1 编码

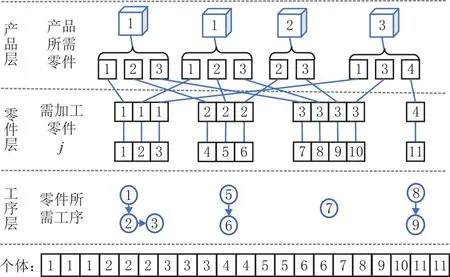
图3 编码方式
3.2 解码规则设计与实验
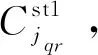

图4 解码过程
3.2.1 加工阶段机器分配规则
采用带释放时间和设置时间的调度问题两种常见分配规则,设置-加工时间最短规则[15](Shortest Process time + Set time,SPST)和最早完工时间规则[7](Earliest Completion Time, ECT)。SPST规则将工序分配到设置时间与加工时间之和最小的机器上,ECT规则将工序分配到最早能够完成加工的机器上。
3.2.2 运输阶段零件分批规则
零件在加工完成后,需先进行运输批次划分,再为批次指派运输车辆。结合问题多阶耦合时序性及层级性,设计两种规则:先完工先运输规则(First Finish First Ship, FFFS)和时间范围内最大载重规则(Maximum Load in Time Range,MLTR)。
(1)先完工先运输规则(FFFS)
仅根据零件加工阶段的完工时间从小到大进行排序,依次从前到后对零件的重量进行相加,若加入后一个零件会导致该批零件总重超过车辆载重,则前面几个零件就会被归为同一批。如图5a~图5c所示,若在含有零件5、4的第一批运输加入零件3后会导致超载,则将零件3放入下一批;第二批在有[3,2,1]的情况下放入零件6会超载,则将零件6单独放入下一批进行运输,最终形成了[5,4]、[3,2,1]、[6]的运输批次和第二阶段的零件运输排序πst2=[5,4,3,2,1,6]。
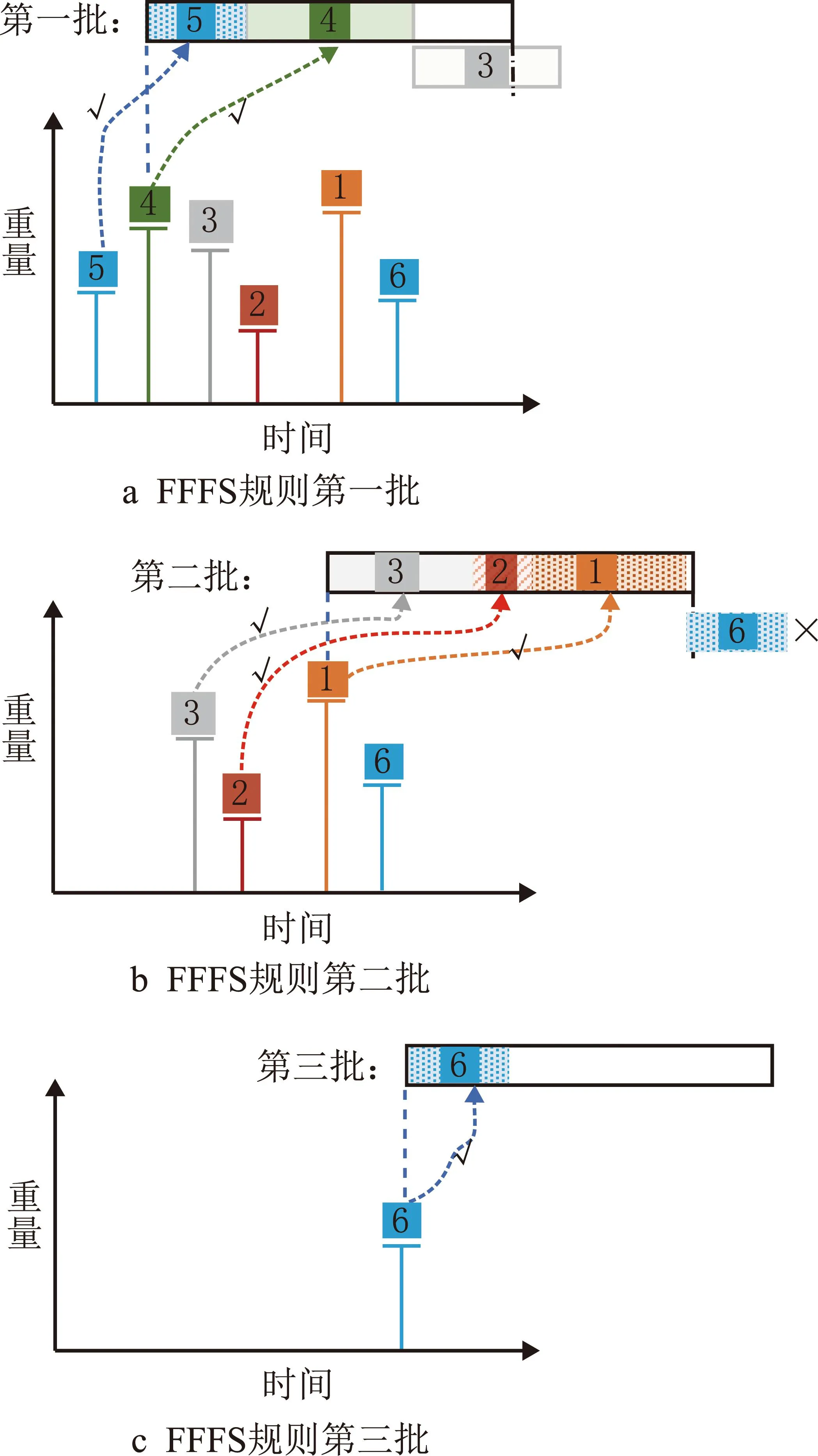
图5 运输阶段分批规则
(2)时间范围内最大载重规则(MLTR)
在FFFS规则的基础上,给定一个时间范围T_range,当下一个零件无法满足载重约束时,考虑T_range内能够满足载重约束的零件。如图5d~图5f所示,加入零件3后无法满足第一批零件的载重约束,考虑T_range范围内的零件2且符合载重约束,则将零件2放入第一批运输中;第二批运输中,零件6在T_range内但不符合载重约束,只能放到第三批运输中,最终形成3个运输批次[5,4,2]、[3,1]、[6]和第二阶段的零件运输排序πst2=[5,4,2,3,1,6]。
3.2.3 产品装配排序规则
完工零件被分批运送到装配阶段后,将被分配到不同产品中完成装配。当运达零件q满足多个产品的装配条件时,为使混装初期能有更多的产品得以装配以平衡整个装配阶段的装配压力,结合问题时序性与层级性设计两种规则:最少零件产品优先规则(Minimum Parts First, MPF)和最多后续可加工产品优先规则(Maximum number of Subsequent Products First, MSPF)。

图6 产品聚合的装配工序排序
πst3生成的步骤如下,其中步骤5利用ECT规则为工序分配装配机器。
算法1少零件产品优先规则(MPF)。
输入:可装配产品(p1,p2,…,pn);
输出:选择可装配的产品choice。
For i=1 To n
令ηi←0.
For q=1 To Q
若pi的装配需要零件q,则ηi←ηi+1.
End
End
算法2最多后续可加工产品优先规则(MSPF)。
输入:可装配产品(p1,p2,…,pn),当前不同零件的拥有量(h1,h2,…,hQ);
输出:选择可装配的产品choice。
For i=1 To n
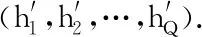
统计(h1,h2,…,hQ)下可装配产品的数量ηi.
End

步骤2构建矩阵[Wab]A×A,若工序a为工序b的紧前装配工序则wab=1,否则为0wab=0(a,b=1,2,…,A);

步骤4W的第a列是否全为0,若a列全为0则表示a没有紧前工序,将a放入待加工数组Μ中;若a列中存在1,则说明a还有紧前工序未完成;

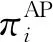
步骤7令i=i+1,若i≤S则返回步骤3,否则结束。
4 HEDA_RH求解MCISP_PC
4.1 个体块结构描述
按上述编码方式,通过对优质个体的统计,出现了一些块聚集现象。一种是块中所有工序均为同一种零件,称为同型聚集块(Homotype Gather Block,HGB)。如图7所示,在3个不同个体中,用同一颜色表示同一种零件,前后颜色相同的块为HGB,如[1 1]、[2 2 3 3]和[ 8 6 9]等。另一种是块中并非所有工序均为同一零件但在优质个体中出现多次的块结构,称为异型聚集块(Isomerism Gather Block,IGB),图7标记长度为3的IGB,如[4 4 1]、[1 1 7]和[7 1 4]等。

图7 IGB与HGB示意图

(13)

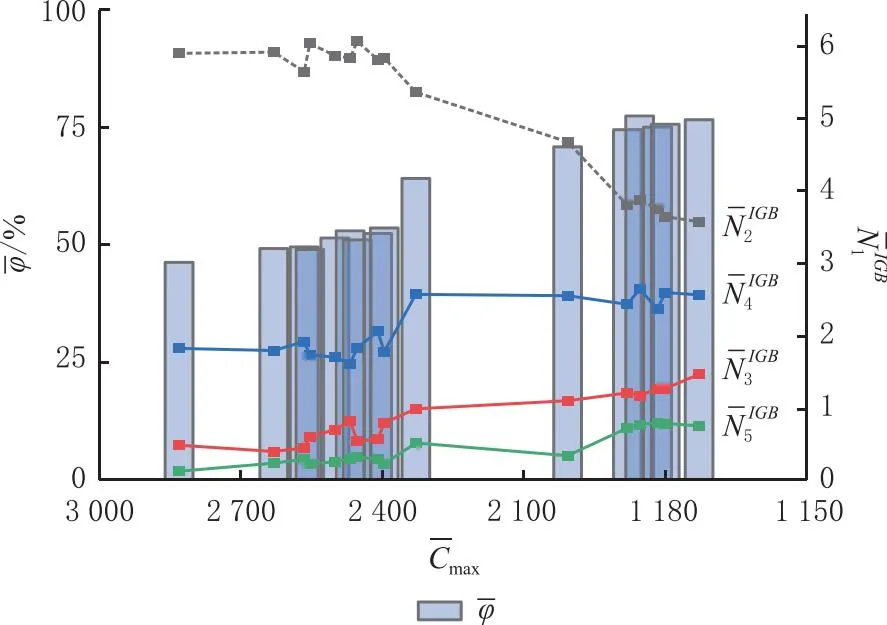
图8 不同值下的和的变化趋势
4.2 种群初始化

步骤1将π0随机分为π和π′两段,两段长度差值小于等于1,令i=1;
步骤2读取πi的零件型号;
步骤3在π′中选取一个同型零件插入到πi后,若π′中没有同型零件则令i=i+1并返回步骤2;
步骤4删除π′中刚插入的同型零件,i=i+1,若i≤L则返回步骤2。
4.3 概率模型初始化与更新
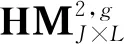
(14)
(15)
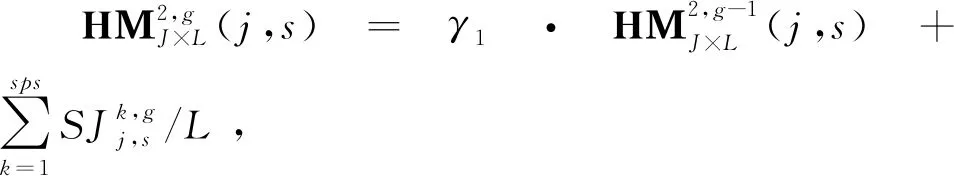
(16)
(17)

(18)
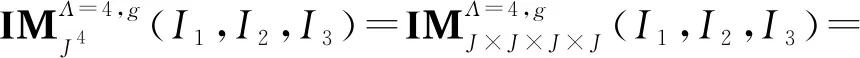
(19)
(20)
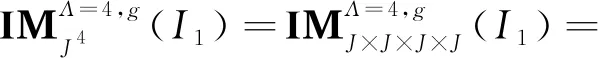
(21)

(22)

(23)

(24)
I1,I2,…,IΛ=1,2,…,J,s=Λ,…,L。
4.4 HEDA_RH采样机制

4.4.1 采样机制Ⅰ:结合HGB记录矩阵的采样
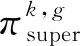

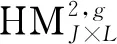
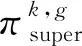
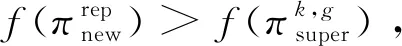

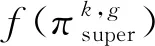

图9 采样机制Ⅰ示意图
4.4.2 采样机制Ⅱ:结合IGB记录矩阵的采样

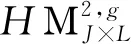
步骤2令sit=Λ,统计零件j还需出现在π中的次数uj;

步骤4根据式(25)计算RInput;
步骤5若uj=0,则将RInput(j)置为0;

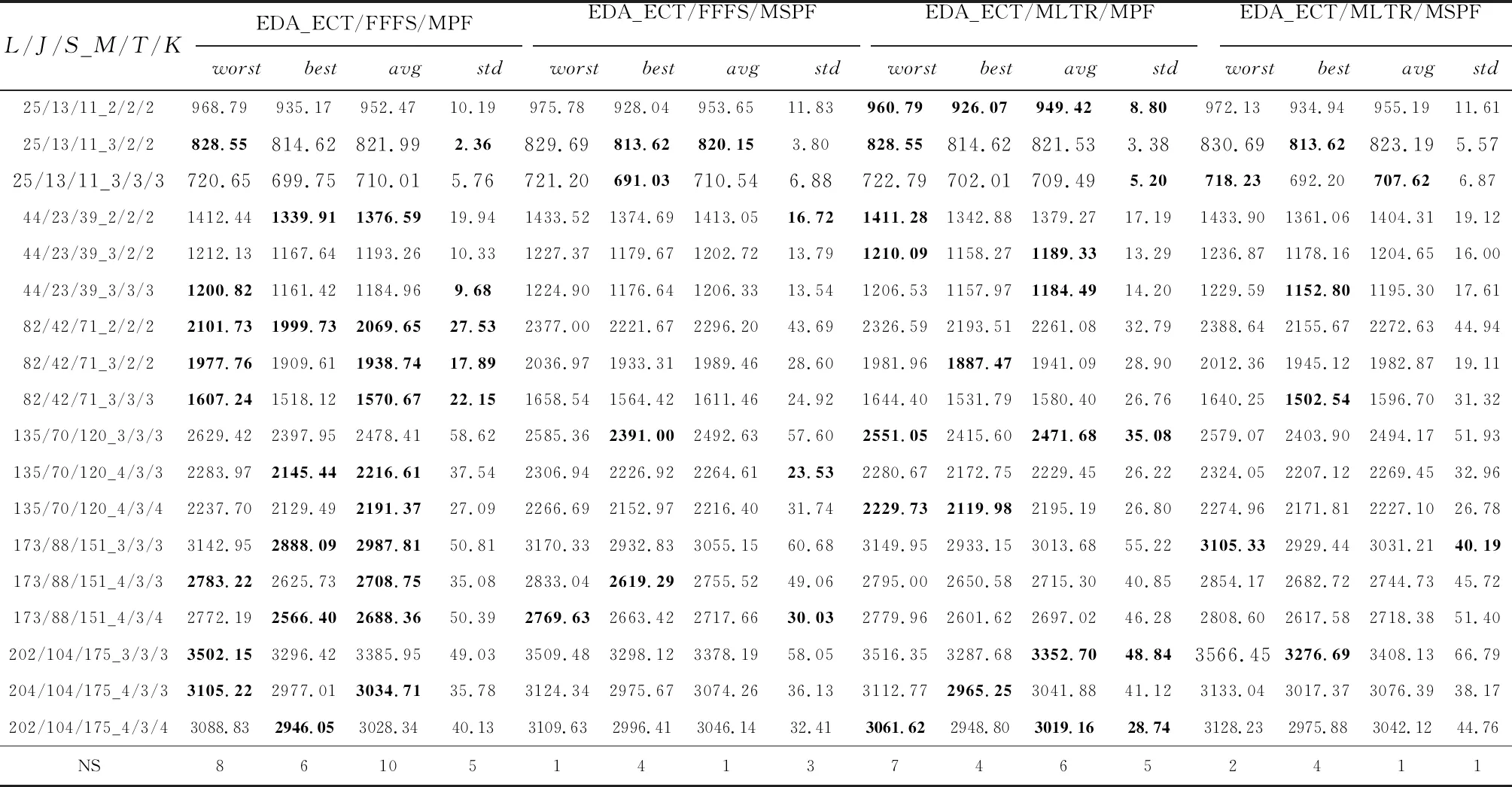
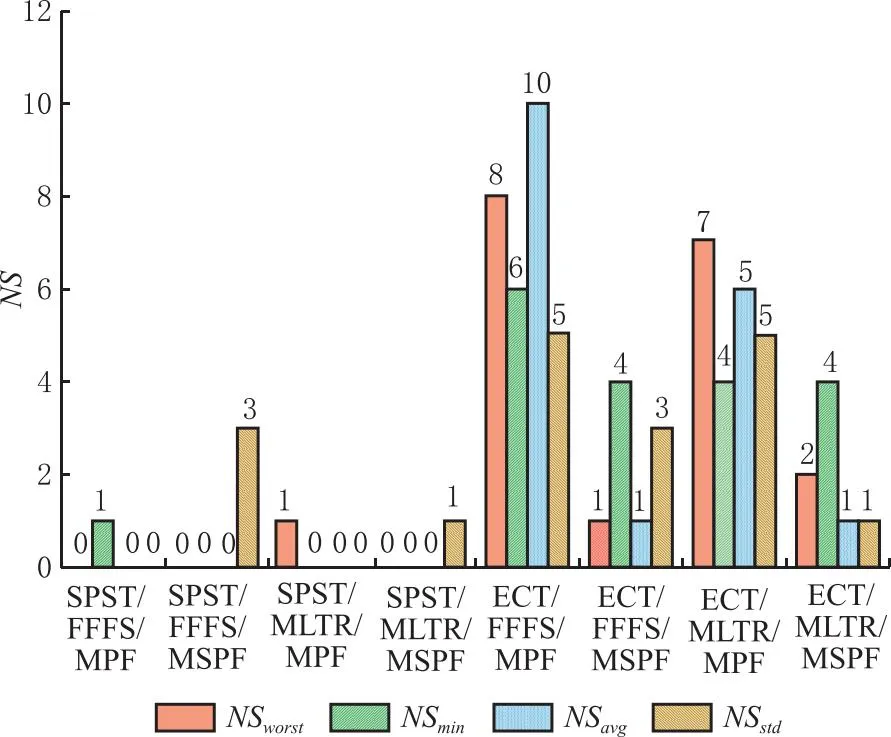
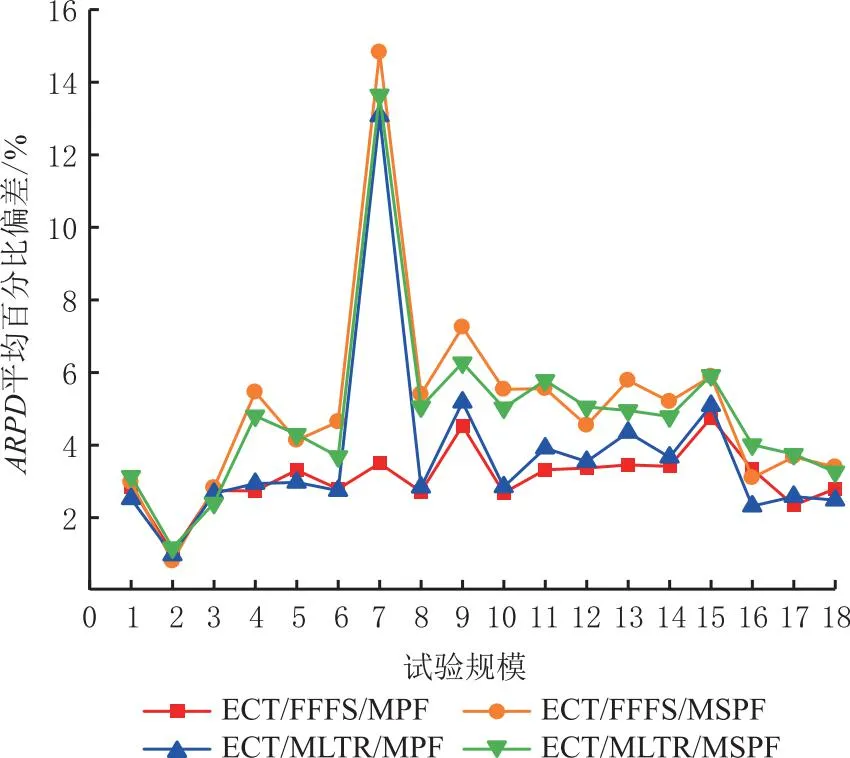
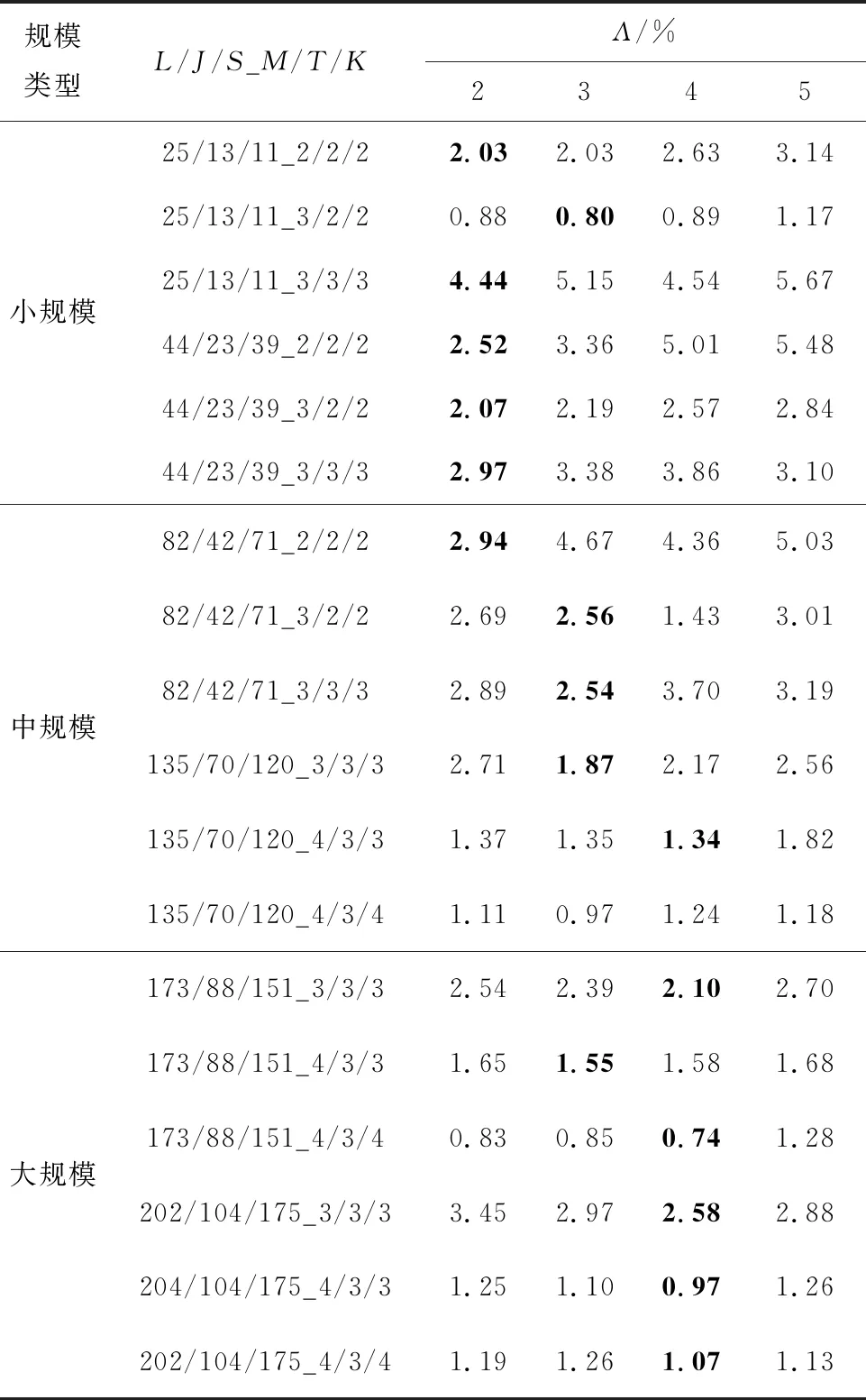
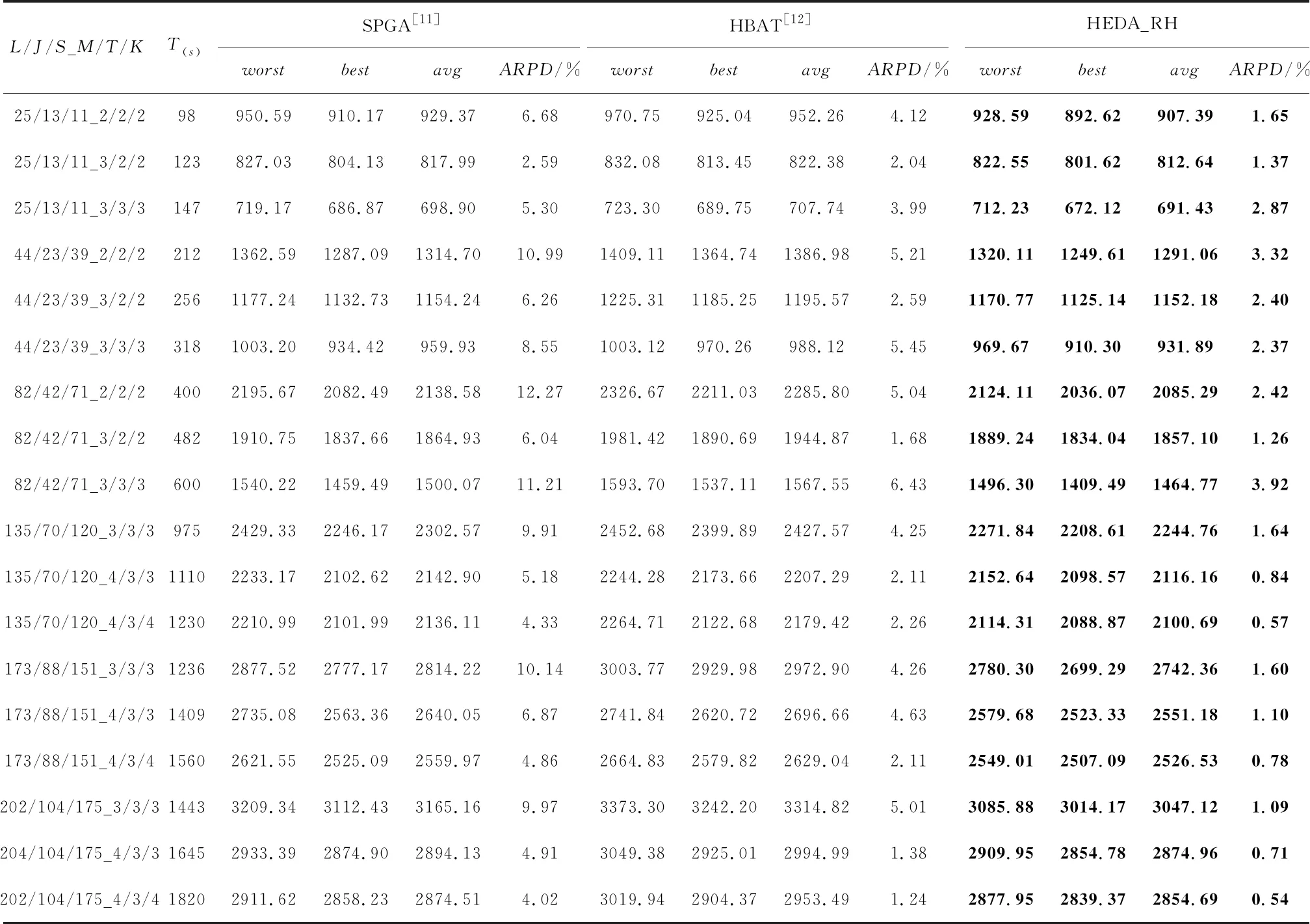
步骤7若sit (25) x=1,2,...,J。 图10为采样机制Ⅱ的采样过程。 图10 采样机制Ⅱ示意图 每一代的新种群都由3部分组成:上一代优质个体比率为α1;采样机制Ⅰ生成的个体,比率为α2;采样机制Ⅱ生成的个体,比率为α3;α1+α2+α3=1。 MCISP_PC解空间庞大,随着问题规模增加会出现解空间爆炸现象,全局搜索虽具有一定的搜索广度但深度有所欠缺,往往无法让算法跳出局部最优。究其原因往往是因为全局搜索深度不够且随迭代次数增加种群多样性逐渐减小。因此,需为算法设计合理有效的局部搜索操作,以兼顾算法搜索深度和种群多样性。HEDA_RH中局部搜索部分结合问题特性设计6种启发式操作,通过矩阵立方启发式操作学习模型,自适应地调整搜索深度、学习启发式规则执行策略。最后通过个体替换策略来提升迭代更新后的个体差异性,从而确保种群多样性。 4.5.1 矩阵立方启发式操作学习模型 (26) (27) (28) (29) (30) (31) 4.5.2 启发式操作 续表1 4.5.3 个体替换策略 (32) (33) (34) (35) 本节设计HEDA_RH求解MCISP_PC。在定义了优质个体中两种块结构基础上,结合问题性质从全局角度设计概率更新模型及两种采样方式,从局部角度设计矩阵立方启发式学习模型自适应地选择6种启发式操作对优质个体进行细致搜索。HEDA_RH的算法具体流程如图11所示。 图11 HEDA_RH算法流程图 本章实验中,MCISP_PC使用L/J/S_M/T/K表示问题规模,其中L/J/S分别表示加工工序数、运输零件数和装配工序数,M/T/K分别表示加工机器数、运输车辆数和装配机器数。所有算法程序均在MATLAB 2021b下编程实现,实验设备为CPU:i7-11800h,RAM:16 GB。实验中产品的物料结构、工序时间和不同规模下产品需求量如https://pan.baidu.com/s/19Jsp3bbBefK3gtGseEe9bQ?pwd=HEDA所示,不同规模的实验运行时间T(s)由问题规模确定,即T(s)=L×M+J×T+S×K,车辆运输速度设为Vtw=V0-0.085×Gtw。 将3个阶段6种规则进行组合得到8种规则组用于MCISP_PC求解,用三元组方式表示一个规则组,如ECT/FFFS/MSPF规则表示3个阶段分别选取ECT、FFFS和MSPF规则,MLTR中T_range设为所有加工工序的平均加工时间。为验证8种规则组在求解MCISP_PC中的有效性,探寻不同规则在不同规模下的求解效率,将8种规则组与全编码求解方式进行对比,在18种不同问题规模下均采用EDA算法进行求解。实验中,全编码(FullCode)指的是对加工工序排列及机器分配、零件运输分批及车辆分配、产品的零件分配、装配工序排列及装配机器分配进行编码求解。全编码求解及8种规则组求解将分别在不同规模下于T(s)内独立运行20次。实验结果如表2和表3所示,表中评价指标best为最优值、worst为最差值、avg为平均值、std为方差,加粗字体为该规模不该指标的最优值,NS为不同求解方式在特定评价指标下获得最优值的次数。实验数据表明:8种规则组均比全编码求解方式获得较大的提升,且随着问题规模的增加提升效果越明显;在大规模实验中规则几乎获得了一倍的提升,通过std值表明在求解稳定性方面均有提高。由图12可看出:规则组ECT/*/*明显优于SPST/*/*;ECT/FFFS/MPF与ECT/MLTR/MPF在四种对比参数下均获得了更多的NS值。 表2 全编码及前四组规则对比实验数据 表3 后四组规则对比实验数据 图12 NS对比直方图 为进一步比较规则组ECT/*/*求解效率,以式(36)计算ECT/*/*在不同规模下的平均相对百分比偏差(ARPD),其中S为当前所求结果,S*为该规模下运行所得最优值,n为实验重复次数。ARPD可反应不同规则所求结果与S*的偏离程度和不同规模下的波动情况,ARPD值越小越好。结合表2和表3与图12和图13,可得到以下结论:①ECT规则效果明显优于SPST规则;②规则组ECT/FFFS/MPF及ECT/MLTR/MPF的求解效果较优。由此确定后续实验中HEDA_RH种群中所采用两种规则组设定RGA为ECT/FFFS/MPF、RGB为ECT/MLTR/MPF来完成解码。 (36) 图13 不同规则ARPD随实验规模变化曲线 5.2.1 关键参数设置 为确定HEDA_RH中关键参数取值,采用试验设计方法(Design of Experiment,DOE)进行参数试验分析。HEDA_RH中所涉及5个参数及选取的4个水平值如表4所示,即需完成规模为L(45)的正交实验。实验规模选取中等规模(82/42/71_3/3/3),采样机制Ⅱ个体比率α3=1-α1-α2。将平均值avg作为测试响应值,每组参数组均分别进行20次独立实验,运行时间同为T(s)=L×M+J×T+S×K。 表4 关键参数水平值 所选测试参数正交表及avg统计值如表5所示,根据正交表得出各参数不同水平响应值、极差和影响力等级如表6所示。由表4~由表6可知,γ1取水平3、γ2取水平4、ξ取水平2、α1取水平2、α2取水平2时算法性能相对较好,且由极差可知α1对HEDA_RH的性能影响最大,其次是ξ、α2、γ1、γ2。综上,HEDA_RH的关键参数设置为γ1=0.85,γ2=0.9,ξ=0.75,α1=0.2,α2=0.4,α3=0.4。 5.2.2 IGB块长度Λ设置实验 表7 不同Λ取值下的ARPD值 由于MCISP_PC为一种新的调度问题,目前尚未有文献对问题进行求解。为验证算法有效性,将HEDA_RH与国际期刊中用于求解与MCISP_PC类似集成调度问题的半置换遗传算法(SPGA[11])和离散蝙蝠算法(IHBA[12])进行比较。SPGA与IHBA均选用文献中设置的最优参数,HEDA_RH关键参数设置同5.2.1节。此外,根据5.2.2节实验结果在小、中、大规模中Λ分别取2、3、4进行实验。对比算法采用规则组ECT/FFFS/MPF计算完工时间,编码同为基于加工工序零件编码。不同算法在18种问题规模下于时间T(s)内分别独立运行20次。表8以worst、best、avg、ARPD为评价指标对实验结果进行统计。图14为6种问题规模下,不同算法的所求结果箱线图,可见随着问题规模的增加HEDA_RH的求解效果越明显。通过上述实验可知,HEDA_RH在18种规模中均较其他两种算法得到了较好值,由此表明了HEDA_RH能有效求解MCISP_PC。 表8 HEDA_RH与SPGA[11]、IHBA[12]对比实验结果 图14 算法对比箱线图 针对考虑装配工艺约束的加工-运输-装配多阶耦合集成调度问题(MCISP_PC),提出一种结合规则启发式的混合分布估计算法(HEDA_RH)求解以最小化最大完工时间为优化目标的MCISP_PC。从复杂系统集成调度在多阶耦合性质下的高效求解方法出发,利用问题多阶耦合特性,采用了只对加工阶段进行编码,后续阶段通过规则组合完成问题解耦与解码。最终将问题耦合特性融入HEDA_RH中,利用个体中出现的两种块结构特征设计采样方式,引导全局解空间搜索方向以提升搜索效率,并设计矩阵立方学习模型对提出的启发式搜索操作进行学习和积累,在提高解质量的同时增加搜索操作有效性。研究内容和结果作为现有调度领域的有效补充,以丰富和拓展求解一类复杂系统集成调度问题思路提供方向。同时,MCISP_PC符合现有一类复杂系统混合企业生产实际,将对应的模型、设计的基于多阶耦合特性的求解方法用于实际生产过程中,能够为提高装配制造企业生产过程的整体效率、降低成本、提升智能化生产水平等方面提供方法指导。 后续研究可围绕MCISP_PC的模型扩展及探寻更加高效的求解方法进行。在模型方面,可考虑更多的生产约束和阶段,或是建立多目标优化模型。在求解方面,可探寻如何通过强化学习方法来简化HEDA_RH中的高维度学习模型。
4.5 自适应矩阵立方启发式局部搜索



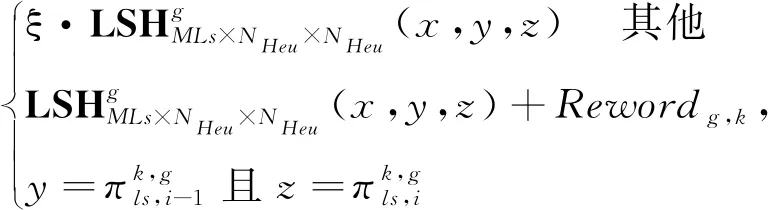
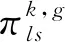

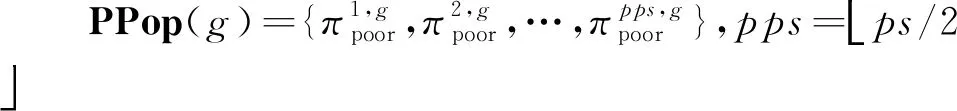
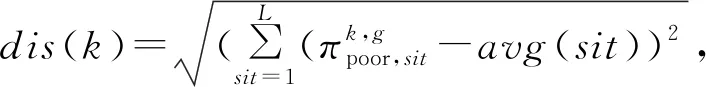
4.6 种群更新策略

4.7 HEDA_RH算法流程

5 仿真实验与结果分析
5.1 规则有效性验证与规则组对比实验

5.2 参数设置


5.3 算法对比实验

6 结束语
