用于皮肤病激光治疗的脉冲光热辐射模型

胡飞凡,徐晨辰,张浩,李东,陈斌,应朝霞

(1. 西安交通大学动力工程多相流国家重点实验室,710049,西安; 2. 陕西省皮肤病防治所,725099,西安)

鲜红斑痣(port wine stain, PWS)是一种常见的皮肤病,多发于面颈部等暴露位置[1],通常由皮肤表面/深层的血管扩张或异常增生引起,严重影响患者的外观和身心健康。基于生物组织的选择性光热作用[2],激光可以实现皮下病变血管的选择性损伤并最大限度地保留正常组织,是目前临床上血管性皮肤病治疗的有效方法。

在皮肤病激光治疗过程中,医生首先对患者进行问诊,观察患处情况,通过对病情的评估选定治疗激光类型,然后根据临床经验及医学文献中常用的激光参数,再结合相关理论知识,最终设定激光治疗仪器的具体参数(脉宽、能量等)。目前,受限于皮肤组织结构的不确定性,仅凭医生观测进行参数选取,治疗效果非常粗糙,常常会加重不良反应,如烫伤、术后疼痛、恢复时间延长及严重并发症等,导致临床完全治愈率已接近10年维持在低于20%的水平[3]。因此,迫切需要对皮肤组织进行内部温度分布与结构的无损测量,为激光热疗参数的选取提供科学依据,有效指导医生开展激光治疗,从而提升治疗效果。

近年来,脉冲光热辐射法(pulsed photothermal radiometry, PPTR)[4-8]应用广泛,作为一种非接触式技术,它利用红外热像仪测量暴露于脉冲辐射(激光)下的样品表面热辐射信号(温升信号)[4],结合有效的重建算法,反演被测皮肤样品初始时刻的温度分布和内部结构。PPTR法无需接触患者皮肤,能避免对组织造成创伤,其测量信号由各个深度的温度信号线性叠加至表面而成,其形式对于温度反演来说为第一类Fredholm积分方程[9]。由于具备这种数学形式的问题往往是严重不适定的,这意味着重建的温升分布通常不唯一,且对测量噪声十分敏感。因此,设计反演算法时需要对问题采取有效的正则化策略。Mahdawi等采用V-循环多重网格法进行迭代,通过数值算例验证了近似解的准确性和计算速度,得到更快的收敛性[10]。随后,他们又改进了求解反问题的Landweber迭代法,并将其应用于求解热传导方程的反边值问题[11]。与此同时,三维反演算法也由于计算机科学技术的飞速发展、计算性能的提升及实际工程问题的需求引起了广泛关注,算法设计也是多种多样。谢正超等采用基于广义交叉验证的Tikhonov正则化和截断奇异值分解法,分别对煤粉锅炉的炉内火焰进行了三维温度场重建,发现 Tikhonov正则化的重建结果误差较截断奇异值分解法要小[12]。刘晓蔚等针对爆炸中温度场的重建难以取得较高精度等问题,在联合代数重建算法(SART)迭代系数中添加惩罚项,实现了更高质量的重建[13]。目前,脉冲光热辐射法无损测量温度分布的效果不断提升,但鲜有学者将其应用于激光手术的温度及结构探测辅助开展激光治疗。

本文围绕常见血管性皮肤病的激光治疗这一主题开展研究,以鲜红斑痣皮肤病为例,采用脉冲光热辐射法构建皮肤传热理论模型,选取合适的正则化策略[14-15]开发温升反演算法,实现了鲜红斑痣患者皮下的温升分布及结构重建,并开展体外实验验证其有效性,最后将其应用于临床实验。研究结果表明:在皮肤激光治疗中,该应用模型可科学选取激光参数,减少医生凭经验选取参数导致的不良反应,能够实现个性化治疗,从而提升了治疗的有效性。

1 数值模型构建

采用PPTR方法重建皮肤结构辅助激光治疗的理论模型如图1所示。首先,以红外热像仪作为表面辐射信号的测量工具,实现皮肤结构的非接触测量,其原理为采用基于脉冲激光照射后皮肤表面温度的衰减变化曲线,重建辐射照射结束瞬间的皮肤温升分布,该温升分布是激光辐射能在皮肤组织内传输、吸收以及皮肤组织导热共同作用的结果[15]。根据生物组织选择性光热效应[2]理论,鲜红斑痣血液层对不同波长的激光具有选择性吸收效应,若选取的激光波长为鲜红斑痣血液层吸收激光峰值所对应的波长,且激光作用时间小于血液层的热弛豫时间,则该重建皮肤内的初始温升分布可准确反映皮肤内血管层的结构信息(如血管层厚度、深度等)。同时,由于人体表皮层对激光同样具有较强的吸收作用,因此该重建温度也可反映表皮层的厚度等结构信息。随后,将探测到的皮肤结构信息根据生物传热模型进行计算机建模、计算和优化,得到最优的激光治疗参数来辅助医生进行激光治疗,从而提升了治疗的精准性、安全性和高效性。

图1 皮肤激光治疗中的脉冲光热辐射模型Fig.1 Model of pulsed photothermal radiation in dermal laser therapy

1.1 皮肤组织传热模型的建立

根据PWS的病症特点[1],可知病变的毛细血管分布较为密集,如图2(a)所示。假定真皮中杂乱分布的PWS血管在真皮内分布均匀,可把PWS病变区简化为具有一定厚度的层状区域,记为PWS层。这种做法对血管分布的处理具有一定的合理性,也可极大地降低生物组织内光和热传播计算的难度,提高了计算效率。此外,由于脉冲激光照射时间远小于热传导所需时间,且皮肤激光手术的径向尺度远大于轴向深度尺度,因此可把该问题简化成一个半无限大平板在半空间中、无内热源的一维非稳态导热问题。根据以上分析,可建立包含黑色素表皮层、真皮层、真皮层中PWS层在内的多层皮肤模型,如图2(b)所示。

(a)鲜红斑痣患者

将图2所示模型假设为一个具有对流边界的、常物性、非稳态、无内热源的一维半无限大平板导热问题,其温度分布符合如下表达式

(1)

式中:ρ为密度;c为比热容;z为模型的深度;t为时间;λ为热导率;T(z,t)为温度分布函数。

皮肤表面的Robin边界条件可表示如下

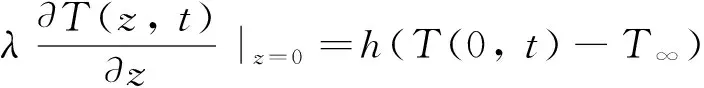
(2)

式中:h为表面传热系数;T∞为皮肤周围的环境温度。

由于红外热像仪捕捉的是温升信号,令热扩散率a=λ/ρc,温升分布函数ΔT(z,t)=T(z,t)-T∞,则式(1)、式(2)描述的定解问题可简化为

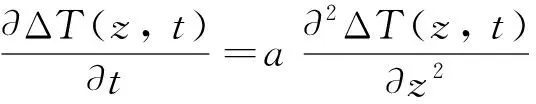
(3)

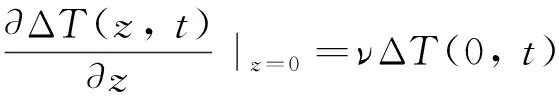
(4)

式中:ν为热损失系数,定义为h/λ,即表面传热系数与热导率之比。

对于式(3)、式(4)组成的定解问题,可采用格林函数法[16]求解,以获得温升分布函数ΔT(z,t),数学解析表示如下

(5)

式中:ΔT(z′, 0)为初始温升分布函数,用于描述处于位置z′的平面热源;erfc(u)为互补误差函数,可写为

至此,通过建立一维模型和采用格林函数法求解正问题,获得了图2(b)所示多层皮肤组织内温升分布函数的解析式,其积分项中包含的初始温升分布函数即是待重建项。

1.2 导热反问题的建立

由于PPTR方法以红外热像仪作为辐射信号的测量工具,因此需要基于红外热像仪的信号测量原理来建立PPTR信号幅度与初始温升分布的关系。红外热像仪测量的表面信号幅度实际上是深度方向的皮下各层组织能量在皮肤表面的沉积,即在脉冲激光照射后,各深度组织辐射力的变化在皮肤表面的线性叠加。以深度为z的组织层为例,若其在激光照射下的温升分布函数为ΔT(z,t),假设该温升远小于环境温度,则深度为z处组织辐射力的变化量ΔEz满足

(6)

式中:ε为实际物体的发射率(黑度);σ为黑体辐射常数,σ=5.67×10-8W·m-2·K-4。

从式(6)可以看出,辐射力的变化量与温升成正比。根据比尔-郎伯定律,光谱辐射能在具有吸收性的介质中传播时将按指数规律衰减。因此,当深度为z处的辐射力变化量传播到皮肤表面时,衰减为

ΔEz0=ΔEzexp(-μaz)∝ΔT(z,t)exp(-μaz)

(7)

式中:μa为组织吸收系数。

由此,表面辐射能量沉积ΔE0,即各深度辐射力在表面的线性叠加,可表示如下

(8)

理想PPTR信号幅度ΔS(t)是由测量的表面辐射能量沉积信号ΔE0经过光电转换处理而来,Milner等研究中推导的理想PPTR信号幅度ΔS(t)公式表达如下[8]

(9)

式中:Cd为红外测量系统决定的比例常数。

将正问题推导所得ΔT(z,t)的关系式,代入式(9)中并对z积分,可得到理想PPTR信号幅度关于初始温升分布的数学表达,形式如下

[erfcx(u+)-erfcx(u1)]}dz′

(10)

式中:erfcx(u)为指数互补误差函数,表达式可写为

erfcx(u)=exp(u2)erfc(u)

其中u1、u-、u+分别为

至此,通过推导构建了理想PPTR信号幅度ΔS(t)与初始温升分布函数ΔT(z′, 0)之间的数学关系。将被积函数中除初始温升之外的其他项整理成核函数K(z′,t),写为

(11)

结合式(10)、式(11),整理可得

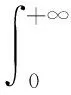
(12)

式(12)即为典型的第一类Fredholm积分方程。对于第一类Fredholm方程的反问题,由于该类问题解的严重不适定性[13],使得ΔT(z′, 0)几乎不存在解析解,因此只能寻求数值解法。接下来,本文基于3种常用的正则化策略,即截断奇异值分解(TSVD)法[17-18]、Tikhonov正则化[19]以及共轭梯度(CG)法[20],对上述方程进行求解。

2 PPTR数值模拟结果分析

针对1.2小节建立的PPTR皮肤结构模型反问题开展仿真模拟,基于上述常用3种算法,定义了基于自定义截断参数选取方法的截断奇异值分解(CTP-TSVD)法、基于L曲线法选取正则化参数[21]的Tikhonov正则化(L-Tikhonov)法以及给定迭代次数的共轭梯度(GNI-CG)正则化算法。3种算法的主函数形式相似,仿真流程可概括为以下5个步骤。

步骤1通过网格划分,将核函数离散成核矩阵。

步骤2除了GNI-CG 算法,其余都需要对核矩阵进行奇异值分解,分别获得左、右奇异矩阵及奇异值向量。

步骤3假设初始温升分布函数为ΔTS(z, 0),代入至线性方程组ΔS(t)=KΔT,获得PPTR理想温升信号ΔS(t),然后基于给定信噪比向ΔS(t)添加白噪声,从而获得含扰动的测量温升信号ΔS′(t)。由于建立的热传导模型中,表皮层、PWS层对脉冲激光的辐射吸收均较强,因而经激光照射后,两层的中心位置具有最大初始温升,然后分别向两边衰减。因此在激光照射结束瞬间,人体皮肤内的温升分布函数ΔTS(z, 0),可认为符合如下超高斯分布

(13)

式中:ΔT1m、ΔT2m分别为表皮层、PWS层的最大温升;z1、z2分别为表皮层、PWS层沿z轴方向的中心位置深度(简称中心深度);d1、d2分别为表皮层、PWS层的厚度;w1、w2分别为表皮层、PWS层的轮廓系数。通过调整上述参数,可模拟激光照射结束瞬间人体皮肤内的温升分布。

步骤4调用正则化参数策略,选取最优正则化参数[18-19],执行正则化方法重建初始温升分布ΔTC(z, 0)。

步骤5绘制重建初始温升ΔTC(z, 0)、原初始温升ΔTS(z, 0)曲线,通过比较两者差异,并基于ΔTC(z, 0)、ΔTS(z, 0)两条曲线之间的差异在ΔTS(z, 0)中的占比,建立如下误差评估函数

(14)

参照文献[7]选取仿真实验参数,通过改变初始温升分布的表皮层厚度d1、PWS层的厚度d2及中心深度z2,来分析3种算法的综合表现。

2.1 表皮层厚度对重建结果的影响

本小节仿真参数选取:a=0.11 mm2·s-1,μa=50 mm-1,ν=0.03 mm-1,h=20 W·m-2·K-1,ΔT1m=1 K,z1=0 mm,ΔT2m=1.5 K,z2=0.23 mm,d2=0.2 mm,w1=w2=1。参考Oltulu等的研究工作[22],保持以上参数不变,选取d1分别为 0.05、0.10、0.25、0.40 mm进行仿真模拟,得到的重建曲线如图3所示。

(a)d1=0.05 mm

由图3可见,在不同表皮层厚度下,3种逆算法都呈现出较好的温升重建结果。随着表皮层厚度增大,PWS层重建深度、温升峰值、厚度(即半峰值展宽,简称展宽)的变化均较小,其中心深度变化不超过0.05 mm(5%),温升峰值变化不超过0.2 K(9.5%),展宽变化不超过0.13 mm(13%)。浅层区域的温升分布逼近精度不高的原因,很可能是由于未能考虑表面对流、辐射等原因对反演过程的影响。总的来看,3种逆算法均可满足不同厚度表皮层结构重建的需求。

2.2 PWS层厚度对重建结果的影响

本小节仿真参数选取:a=0.11 mm2·s-1,μa=50 mm-1,ν=0.03 mm-1,h=20 W·m-2·K-1,ΔT1m=1 K,z1=0 mm,d1=0.05 mm,ΔT2m=1.5 K,z2=0.23 mm,w1=w2=1。保持以上参数不变,选取d2分别为0.2、0.4、0.6、0.8 mm,所得的重建结果如图4所示。

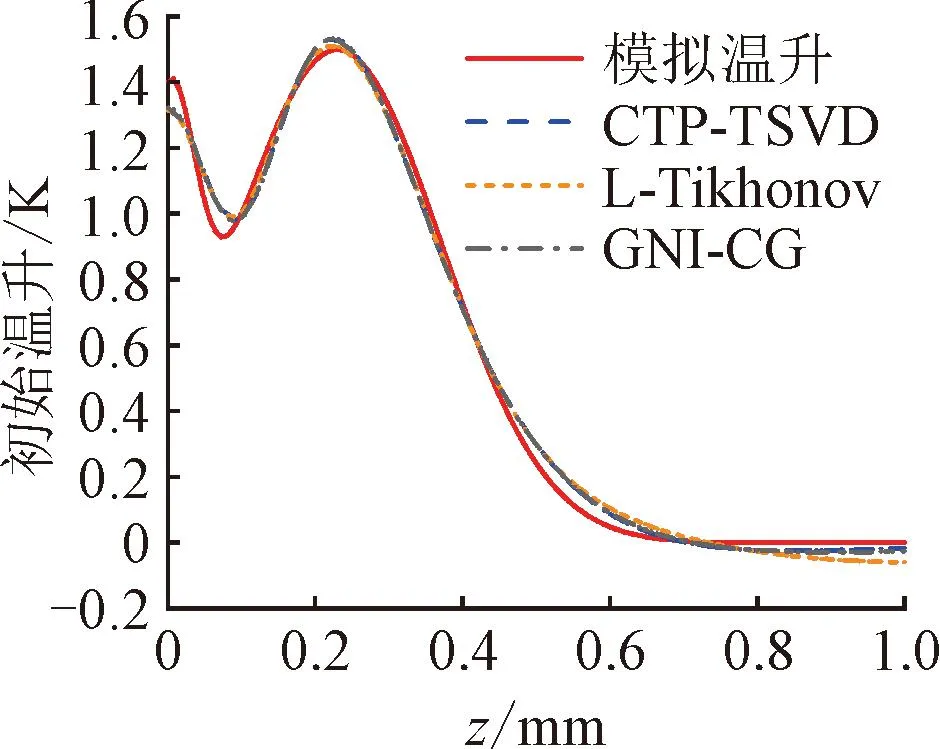
(a)d2=0.2 mm

由图4可见,随着PWS层厚度增加,3种逆算法的重建效果整体均较好。PWS层的重建深度、温升峰值、厚度变化仍较小,其中心深度变化不超过0.1 mm(10%),温升峰值变化不超过0.1 K(6.7%),展宽变化不超过0.12 mm(12%)。这主要是因为PWS层厚度的增加使得温升信号占比增大,从而能更多地反映PWS层的信息,因此重建效果较好。

2.3 PWS层中心深度对重建结果的影响

由2.1和2.2小节可知,表皮层、PWS层厚度的改变对3种逆算法的重建效果影响不大。下面分析PWS层中心深度对重建结果的影响,仿真参数分别选取:a=0.11 mm2·s-1,μa=50 mm-1,ν=0.03 mm-1,h=20 W·m-2·K-1,ΔT1m=1 K,z1=0 mm,d1=0.05 mm,ΔT2m=1.5 K,d2=0.2 mm,w1=w2=1。保持以上参数不变,选取z2分别为0.23、0.43、0.63、0.83 mm,得到的重建曲线如图5所示。

(a)z2=0.23 mm

由图5可见,在PWS层中心深度为0.23 mm处,重建曲线与模拟初始温升吻合度较高,但随着PWS层中心深度增大,重建效果变差,具体表现为:①PWS层重建深度发生偏移,当中心深度增加至0.83 mm时,偏差最大达到了0.12 mm(14.5%);②PWS层温升峰值降低,当中心深度增加至0.83 mm时,温升峰值最大降低了0.4 K(26.7%);③重建PWS层展宽明显增大,当中心深度增加至0.83 mm时,重建展宽增大了0.23 mm(23%)。由此可见,PPTR温升反演技术的使用深度有限。然而对于大部分PWS层来说,其中心深度均保持在0.4 mm以内[23]。由图5(b)可见,当PWS层中心深度为0.43 mm 时,深度方向反演的相对误差较小,评价指数的最大值小于0.18,PWS层的重建深度、温升峰值、厚度变化较小,其中心深度变化不超过0.05 mm(5%),温升峰值变化不超过0.1 K(6.7%),展宽变化不超过0.08 mm(8%),均在可接受范围内。

2.4 综合性能评价

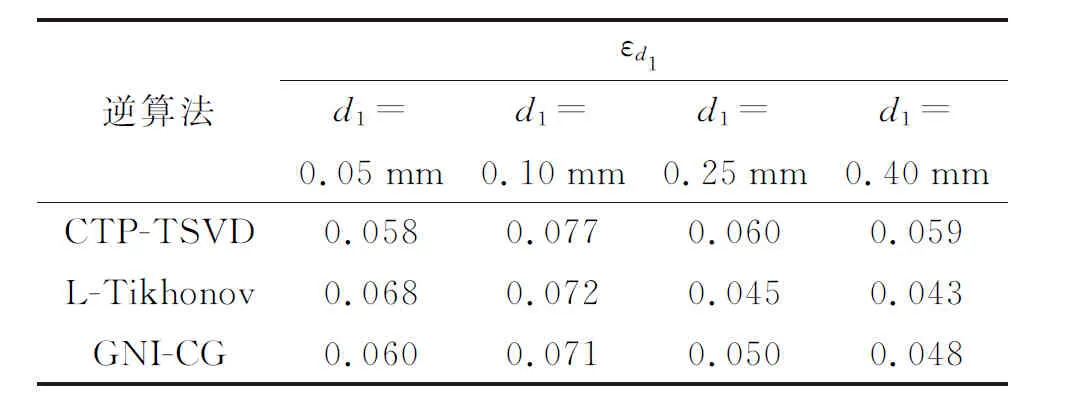
表1 各逆算法在不同表皮层厚度下的评价指数Table 1 Evaluation index of each inverse algorithm under different epidermal thicknesses

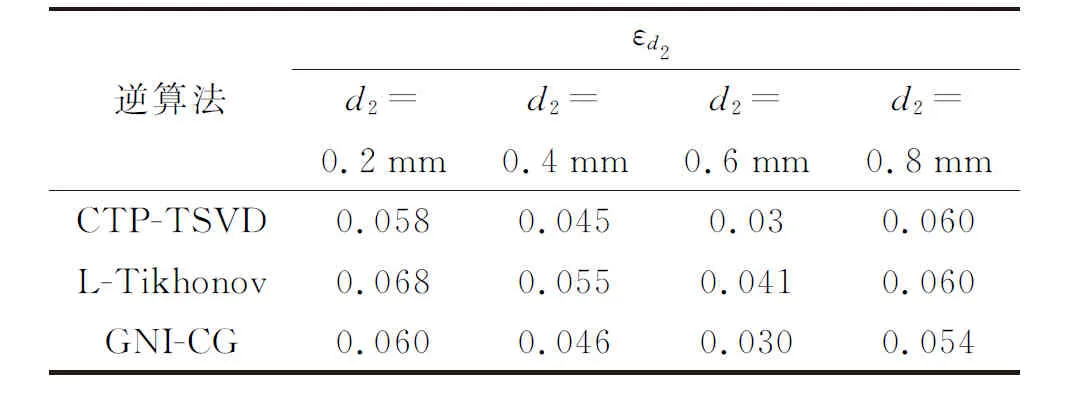
表2 各逆算法在不同PWS层厚度下的评价指数Table 2 Evaluation index of each inverse algorithm under different PWS layer thicknesses

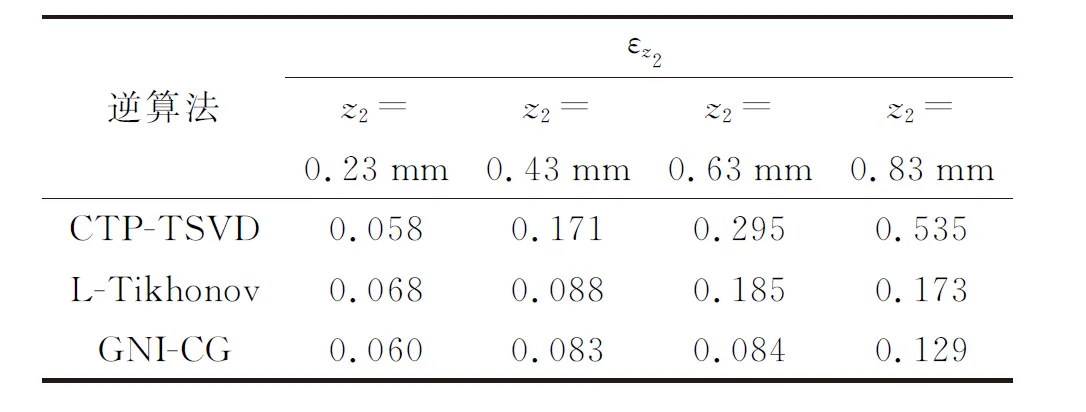
表3 各逆算法在不同PWS层中心深度下的评价指数Table 3 Evaluation index of each inverse algorithm at different PWS layer central depths

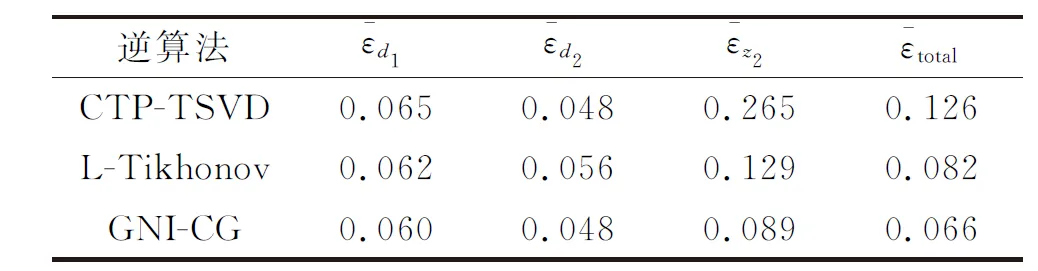
表4 各逆算法的综合评价指数Table 4 Comprehensive evaluation index of each inverse algorithm

综上,L-Tikhonov正则化和GNI-CG正则化算法相较于CTP-TSVD算法的综合评价指数更小,表明前两者的综合表现比CTP-TSVD算法更优秀。下一步,我们将选取最优的GNI-CG算法进行实验验证。

3 实验研究

上节通过数值模拟验证了算法的有效性,结合理论分析证明了采用PPTR法进行皮肤结构探测的可行性。本节将针对临床应用开展体外仿体实验,进一步验证皮肤组织结构探测的有效性。采用PPTR方法对二附院患者进行皮肤组织的温升分布求解及结构信息探测,将探测到的信息用于激光参数选取,从而达到辅助医生激光治疗的目的。

3.1 皮肤仿体制备

皮肤仿体的制备流程如下:首先将3 g琼脂粉溶解在100 ml蒸馏水中,然后加入2 g脂肪乳剂增加散射性,接着将混合物加热至沸点引发聚合,最后将适量聚合琼脂溶液注入小型培养皿,制备表皮层,将适量聚合琼脂溶液注入大型培养皿,制备真皮层,鲜红斑痣PWS层为厚度50 μm的粉红色聚乙烯箔,3层的结合在水浴中开展以防止相邻层之间形成气泡。在吸收层下放置薄膜热电偶,测量激光照射后吸收层的温度。图6(a)为制备的皮肤仿体,图6(b)为红外相机拍摄的图像。

(a)皮肤仿体

3.2 皮肤仿体实验流程

采用脉冲激光器、红外相机、计算机、皮肤仿体搭建如图7所示的PPTR实验台。使用的激光波长为1 064 nm,能量为10 J/cm2;脉冲形式为单脉冲,宽度为1 ms,光束直径为5 mm,入射角θ为45°。同时采用帧率为120 Hz、记录波段长度为7.5～13.5 μm的红外相机采集仿体表面温度信号,记录时间为1.5 s。将采集到的表面温度信号传输至计算机,采用逆算法重建获取皮下温度分布。

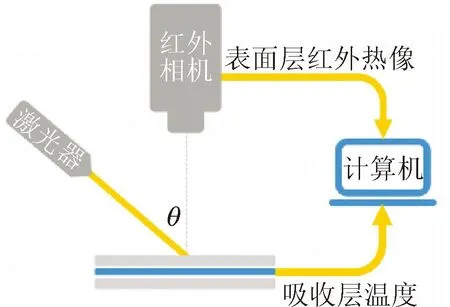
(a)示意图

3.3 皮肤仿体实验结果

图8给出了PWS层中心深度z2为0.2、0.4、0.6 mm时,温升重建结果与实验值的对比。图9给出了PWS层深度、展宽、最大温升的重建结果与实验值对比。从图8～图9可以看出,PWS层中心深度越浅,重建效果越好,无论是PWS深度、展宽、最大温升,都与实验值更为接近。当PWS层中心深度为0.2 mm 时,PWS层重建深度与实验值高度重合,误差低于0.1%,展宽的重建误差为4%,最大温升的重建误差为3%。随着PWS层中心深度增加,重建深度仍与实验值保持较高重合度,误差最大为2.5%。随着PWS层中心深度继续增加,在0.8 mm处,重建展宽逐渐增大,与实验值相差0.061 mm,误差为122%;重建的最大温升与实验值相差4.15℃,误差达到了25.8%。由此可见,随着PWS层中心深度增加,PWS层深度、最大温升的重建效果均较好,但重建展宽即PWS层厚度的误差却显著增大,这主要是因为经过组织的吸收,传输到表面的深层辐射信号随着PWS层中心深度的增加而减弱,在诸如环境噪音等因素的干扰下,重建精度减弱。因而在实际应用中,需要根据图9(b)的误差曲线对展宽进行修正。

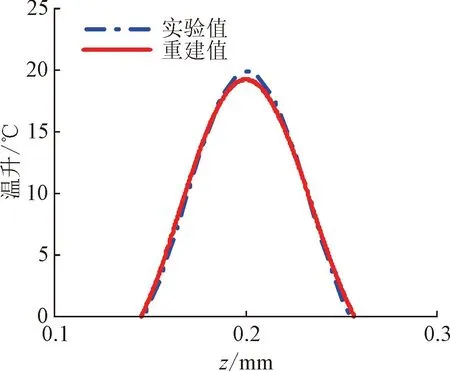
(a)z2=0.2 mm

3.4 临床实验结果

鲜红斑痣的激光临床治疗过程中,如波长、脉宽、入射能量等激光参数的选取对治疗效果起着决定性的作用。以入射能量为例,若能量过低,病变血管无法得到有效清除;若能量过高,则会引发表皮烫伤等副作用。目前,由于缺乏有效的皮肤结构检测技术,激光参数的选取主要凭借医师临床经验,而无法根据每位患者具体的皮肤情况实现个性化治疗。以美国Candela激光公司波长为595 nm的Vbeam激光治疗仪为例,其可选取的参数范围包括:脉宽为0.5～40 ms,入射能量为0～20 J/cm2,频率为1～10 Hz。如何在如此多的参数中选出最优参数组合,对于医生来说十分困难。因而临床医生迫切需要患者皮肤结构探测、激光参数智能化选取的技术和手段。本文提出的脉冲辐射法在临床应用过程中,首先可基于该方法反演出个性化患者的皮肤组织结构,其次可基于该皮肤结构信息,利用已有的参数优化软件帮助医生选取治疗参数,辅助开展激光治疗。

实验的具体实施过程如图10～图11所示。首先,用安全激光剂量2 J/cm2照射患者面部皮肤表面,如图10(a),开展PPTR测量。然后,采用红外热像仪探测皮肤表面温度,如图10(b),提取并处理激光作用区域的温度信号,如图10(c)。最后,利用逆算法根据探测信号,反算皮下组织的初始温升分布和皮肤组织结构信息,如图11。

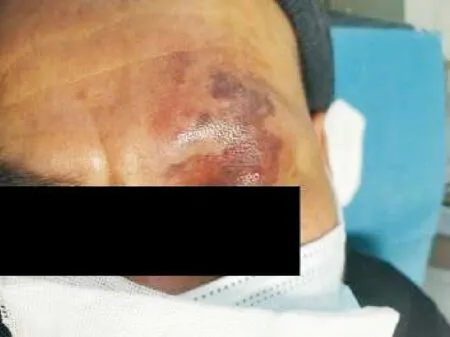
(a)患者面部

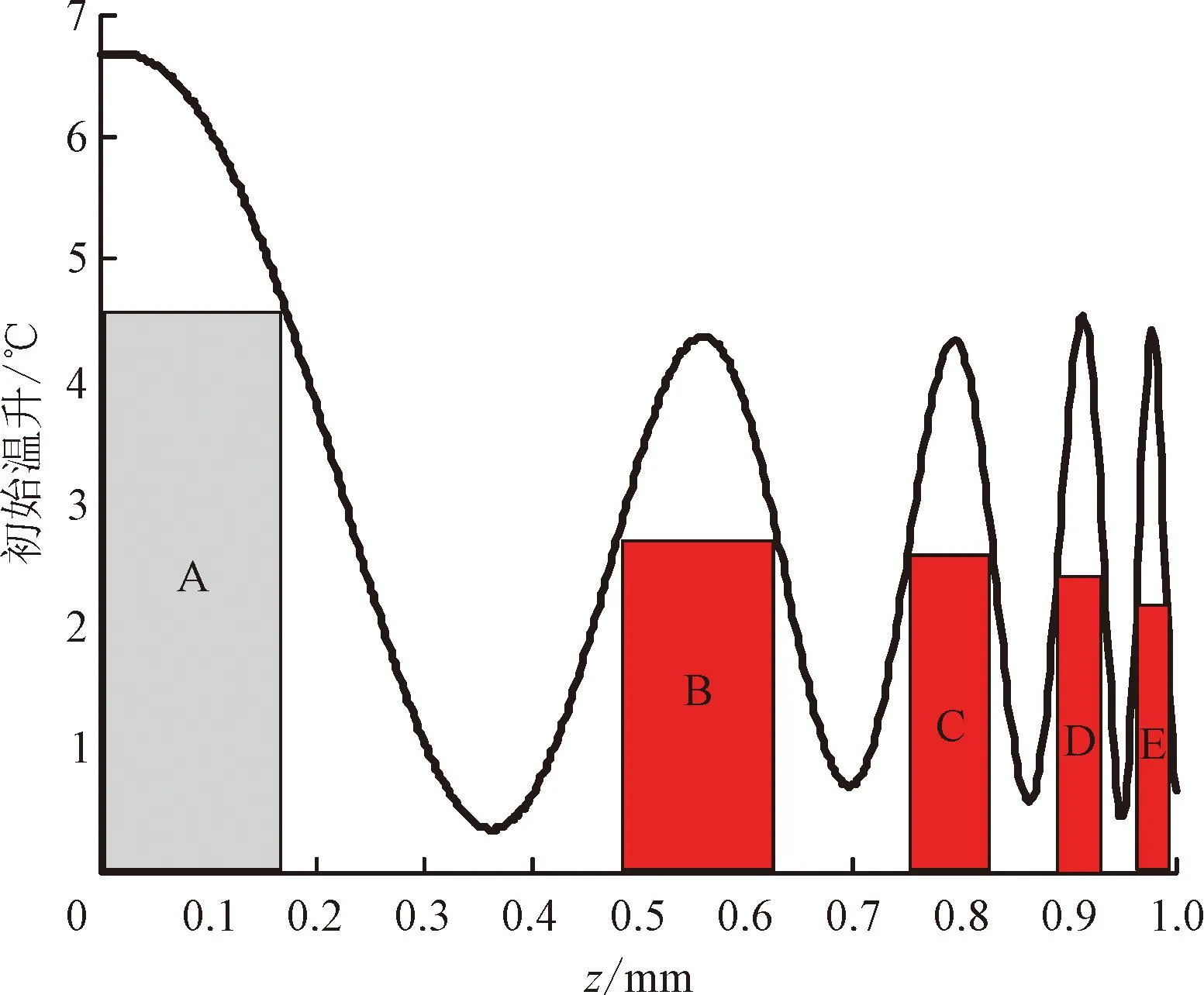
图11 皮下初始温升分布重建结果Fig.11 Reconstruction of the initial subcutaneous temperature rise distribution

图11中,紫色区域A代表具有黑色素的表皮层,红色区域B、C、D、E均代表病变血管。由于激光的作用,表皮层及PWS层在吸收激光能量后瞬时升温,呈现高斯温峰形状。由于重建的血管深度较深,为避免展宽重建误差过大,利用图9(b)的误差曲线对展宽结果进行了修正。修正完成后,根据图11,可估算出表皮层厚度dA=0.18 mm;血管B位于zB=0.55 mm处,厚度dB=0.088 mm; 血管C位于zC=0.79 mm处,厚度dC=0.032 mm; 血管D 位于zD=0.91 mm处,厚度dD=0.021 mm; 血管E位于zE=0.98 mm处,厚度dE=0.01 mm。上述重建结果均符合患者面部特征下的皮肤结构参数范围。此外,本模型对于皮下血管温度的重建效果较好,有望实现激光热疗过程中的温度在线监测。

基于PPTR方法进行皮肤结构探测,反演出患者的皮肤结构信息后,可采用激光参数优化软件[24](图12)进行治疗参数优化,软件的计算过程如下。

图12 参数优化软件界面Fig.12 Parameter optimization software

步骤1以经典的多层均匀模型为基础,构建出患者的皮肤结构模型。

步骤2基于光传输模型[25],计算激光能量在患者皮肤内的传播及分布情况。

步骤3基于生物传热模型[25],计算激光作用后皮肤组织的温度分布。

步骤4基于热损伤模型[26],以PWS层血管达到损伤阈值为条件,进一步优化如脉宽、能量等治疗参数。

针对图10(a)中的患者,利用脉冲光热辐射模型反演的个性化皮肤结构如图11所示,在激光参数优化软件内输入结构参数信息后,即可得到推荐的激光治疗参数,如图12所示。最终医生可以此为依据,选取合适的激光参数对患者开展治疗。

4 结 论

本文针对血管性皮肤病激光热疗中,激光参数选取无依据、临床疗效不佳的瓶颈问题,提出了一种基于脉冲光热辐射法重建皮肤结构,智能化选取激光参数用以辅助激光治疗的模型。采用脉冲光热辐射法建立数值模型,利用MATLAB软件开展仿真实验,通过调整模型轮廓等参数,全面分析了CTP-TSVD、L-Tikhonov以及GNI-CG 3种正则化逆算法对皮下血管深度、厚度及温度的重建效果,发现GNI-CG正则化算法的综合性能最好,L-Tikhonov正则化算法综合表现次之,CTP-TSVD算法的综合表现最差。然而无论何种方法,对血管层深度及温度的反演精度均较好,而对血管层厚度的反演精度稍差,需要采用实验值进行修正。接着,基于模拟结果进一步开展体外实验,验证了模型的有效性。最后,将最优算法GNI-CG应用于临床研究,为临床医生的激光光热治疗血管性皮肤病提供了定量化的数据支持。