基于主成分分析的多重定量PCR荧光串扰校正

王 鹏, 王振亚, 汪 舜, 张 杰, 张 哲, 杨天航, 王弼陡1, *,罗刚银1, *, 翁良飞, 张翀宇, 李 原

1. 中国科学技术大学生物医学工程学院(苏州), 生命科学与医学部, 江苏 苏州 215163

2. 中国科学院苏州生物医学工程技术研究所工程化研究中心, 江苏 苏州 215163

3. 重庆国科医创科技发展有限公司分子诊断中心, 重庆 400700

引 言

聚合酶链式反应(polymerase chain reaction, PCR)是分子生物学常用的检测手段, 能够检测生物特定DNA和RNA的浓度, 对疾病诊断、 法医鉴定和食品安全检测等应用有重要的意义[1-5]。 其主要原理是在PCR过程中, 加入能够与待测核酸反应的特定荧光基团, 通过检测荧光值的上升, 推算核酸量的增加过程。 理论上, 检测到的荧光值大小, 能够对应已反应荧光染料的浓度, 可以推算出核酸的量。

在实际操作中, 由于激发光谱和发射光谱的重叠以及滤光片过滤带宽限制带来的荧光串扰, 使测得的信号无法真实反映被测目标的准确值。 研究中主要采取以下几种解决方式来减少串扰带来的影响, (一)通过系统设计, 如滤光片选择或分时复用等方式, 最大限度地减少干扰的存在。 如Lewis等采用分时复用的方式将各波段的激光脉冲及对应染料的荧光信号在时间上分离, 消除了传统DNA测序技术的光谱串扰[6]。 该方法降低了对染料的要求, 但对所用荧光染料仍有所限制。 (二)根据系统采用的硬件参数, 正向计算获得荧光补偿系数。 如Geißler等设计的FRET生物传感器, 其补偿矩阵中各元素通过荧光光谱直接计算获得[7]。 Liu等同样是通过荧光光谱获得串扰数据, 获得了待测对象的精确测量结果[8]。 以上方法均是根据硬件的物理参数进行计算荧光补偿矩阵中各个元素的具体值。 实际系统往往与理论值有些许偏差, 再加上激发光和发射光的叠加影响, 导致计算过程复杂。 还有一种比较常用的确定串扰的方式, 通过实验反向求解串扰系数。 Yin、 Li和Huang等分别在各自的DNA测序研究中, 采用四维空间聚类方法, 通过迭代计算, 确定荧光强度分布和染料浓度之间的映射关系[9-11]。 Domnioru等提出利用信号的强度差异代替信号本身来进行计算, 使得无需基线调整, 即可实现串扰校正的目的[12]; 该算法主要是针对4种及以下不同的荧光的分离与分析, 对于4种以上染料组合讨论较少。 对于4种以上荧光串扰的计算, Gothot等通过实验获得线性方程组的各个系数, 从而得到荧光补偿矩阵[13]。 在补偿效果评估方面, Li等在研究中提出了一种定量方法来评价串扰校正的质量[11]。 臧留琴等在标准迭代四维聚类分析的基础上提出了一种对串扰矩阵进行估算的方法[14]。 以上方法实验操作过程繁琐, 或需要通过多次迭代才能获得比较理想的补偿矩阵。

主成分分析(principal component analysis, PCA)是一种常见的数据分析方式, 常用于高维数据的降维, 可用于提取数据的主要特征分量。 目前已有研究者将其应用于微弱信号分离。 Hasegawa提出了利用主成分分析检测混合光谱中微弱光谱变化的方法[15-16]。 有研究采用流式细胞术对蓝细菌进行光谱流式检测时, 提出利用主成分分析、 多元曲线分辨以及交替最小二乘法得到纯组分光谱及其组分浓度。 该方法计算量小, 能够快速定位获得目标数据。

本研究将主成分分析方法应用于荧光定量PCR测量过程中的荧光补偿, 适用于4色及以上的多重荧光补偿。 本方法不需经过迭代, 即可获得补偿矩阵, 有效地减少计算量。 采用得到的荧光补偿矩阵去除非目标通道的荧光串扰, 可实现荧光通道数据的解耦。

1 理 论

在多重荧光定量PCR设备的设定中, 各染料理论发射荧光值记为“染料向量”F, 各通道的检测值记为“检测向量”R, 理想情况下F等于R, 但在实际操作中, 由于滤光片的选择、 光谱重叠等因素影响, 导致测得的“检测向量”R无法直接用于表示各染料的实际浓度值。 向量F与向量R之间关系如式(1)。

R=MF

(1)

式(1)中, 转换矩阵M为n×n的方阵,n为荧光染料/检测通道数量, 该矩阵即为荧光串扰矩阵。M的列向量表示某染料在各个检测波长下的荧光强度。 计算的目标是针对特定系统得到矩阵M, 但在实际检测中, 由于无法直接获得“染料向量”F中各元素的理论值, 因此无法通过方程线性求解系数的方式进行计算。

为了方便描述, 考虑二维数据情形, 假设有两种荧光染料dye1和dye2及其对应检测通道channel1和channel2, 当取不同浓度的dye1进行实验时, 由于荧光光谱的重叠, 会有部分荧光进入到channel2中, 实验得到的数据将如图1所示, 其中X轴为channel1数据,Y轴为channel2数据。 在系统硬件一定的情况下, 可以看出dye1在channel1和channel2中的比例相对固定, 其中的数据波动来源于测量误差。 计算荧光串扰, 就是要确定dye1在各通道中的读数比例。

图1 两通道数据分布和其降维后的投影向量

主成分分析是数据分析中常用的降维方法, 其原理是通过寻找一组新的坐标系, 将原始数据投影至该坐标系下, 同时最大限度地保留原始信息。 将其原理应用于串扰补偿, 对于二维坐标系的情形, 若想进行降维, 很容易观察到, 图1中e所指的方向即为将来降维后新坐标系的基。 因此通过主成分分析方法, 找到其第一主成分, 其所代表的方向即指出了染料在各个通道的分布情况。 以上是在两个通道的情形下进行计算, 当通道数增多时, 该计算方法的优势将更加明显。

将上述方法拓展到n个染料的情况, 当采用某个单一染料进行实验时, 将会得到不同浓度的该染料在各个检测通道荧光分布情况, 测得的数据组成一个n×i的矩阵, 其中n为通道数,i为实验次数。 对该矩阵中的数据进行主成分分析, 得到第一主成分。 新得到的“主成分”所表示的并不是某一通道的荧光值, 而是一种抽象的混合荧光; 虽然如此, 但是该主成分所表示的向量, 明确地给出各荧光通道所占比例。 通过将该主成分旋转, 即可反向计算得到该染料真正的荧光值或者相对荧光值, 同时其对其他通道的串扰也得到了量化, 通过计算将该部分串扰从其他通道中剔除。 对其他通道染料进行同样的单一染料实验和分析, 可以获得其他染料的主成分向量。 将得到的n个主成分向量分别作为矩阵的n个列向量, 即可获得矩阵M。

2 实验部分

2.1 测试平台

设计了如图2所示检测光路, 激发光路由LED光源、 准直透镜、 激发滤光片、 二向色镜及荧光收集透镜组成, 激发光激发样品管内荧光物质, 发射的荧光经过荧光收集透镜、 二向色镜、 发射滤光片、 荧光聚焦透镜, 由探测器接收。

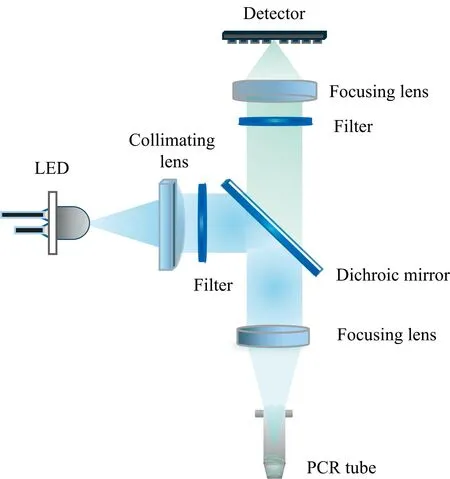
图2 光学原理图

在系统设计时, 选择合适的激发和发射滤光片对, 以优化激发光收集, 同时最小化荧光团之间的串扰。 由于很多荧光物质的斯托克斯位移只约30 nm, 因此要求激发和发射滤光片必须有矩形化的通带波形和较高的截止深度。 各通道选用LED激发光源均具有特定的光谱曲线, 在保证充分激发功率的同时, 还需要考虑荧光基团之间的串扰和其他通道激发光之间的串色问题。 其主要矛盾为: FAM、 HEX、 ROX、 Cy5的发射波长分别与HEX、 ROX、 Cy5、 Cy5.5的激发波长有一定程度的叠加, 因此在考虑较高的检测效率和信噪比的同时, 应尽可能减少光谱重叠。 基于上述原理, 所选择的5通道滤光片组合及二向色镜参数见表1。

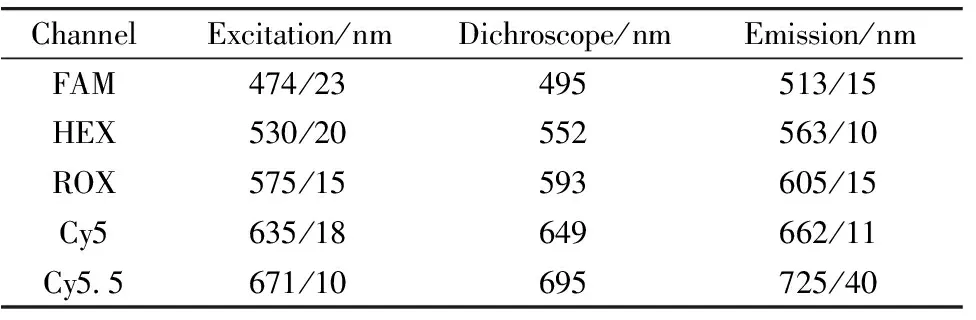
表1 实验平台所用光学元件参数表

5种染料的荧光发射光谱及本实验平台所选择的检测通道如图3所示。 由图3可以看出, 选择的硬件可以将大部分非目标通道荧光过滤掉, 但在各目标通道内, 仍或多或少的混入了其他荧光染料的发射光。

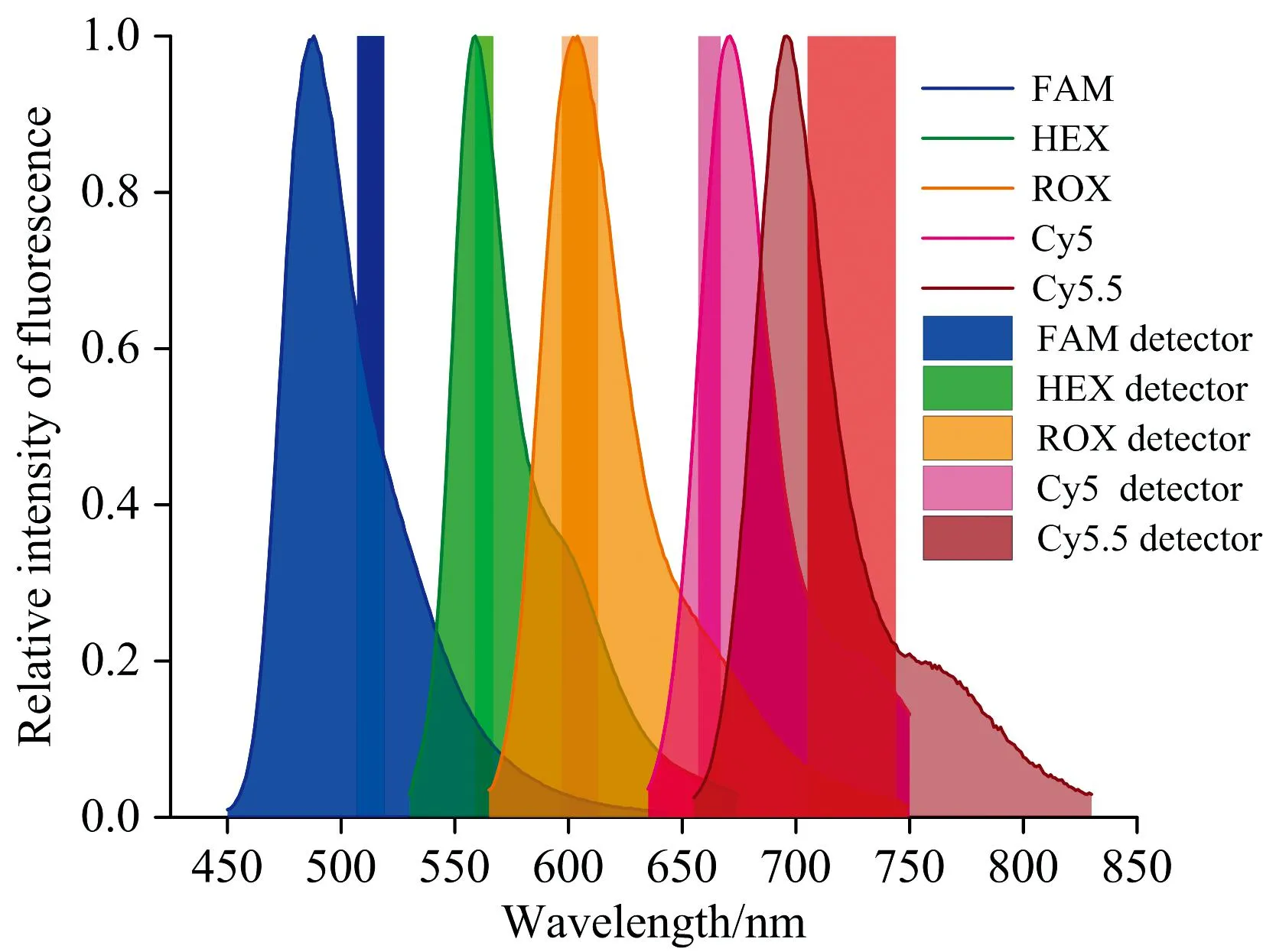
图3 染料的荧光光谱及对应检测通道

2.2 试剂

研究了FAM、 HEX、 ROX、 Cy5和Cy5.5五种染料的光谱串扰。 染料采购自ThermoFisher, 相关信息见表2。 采用凯基生物的磷酸盐缓冲液(PBS, 货号: KGB5001)作为稀释剂进行染料稀释。

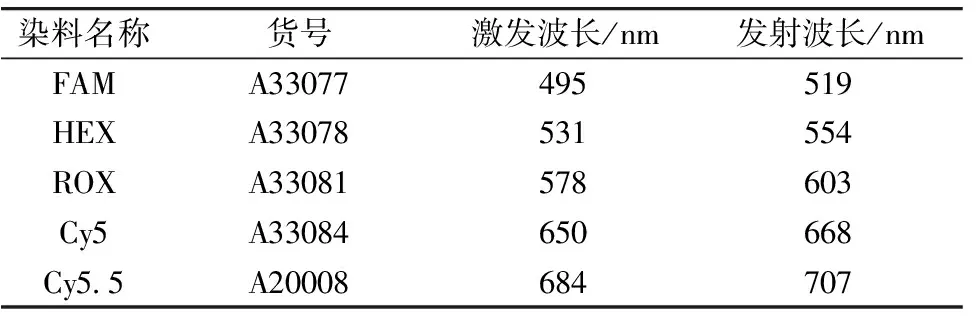
表2 测试所用试剂信息

2.3 补偿矩阵的确定

补偿矩阵的测试需进行单一染料实验。 在实验开始前, 需先确定系统荧光染料浓度线性范围。 将5种染料分别稀释8个梯度, 为了减少实验误差, 每个梯度进行3重复, 10 min内连续读取, 对读取的荧光检测数据进行分析, 确定染料的线性范围, 同时确定各染料的荧光背景。

分别在各染料浓度线性范围内, 再选取16个浓度梯度, 加入PBS稀释剂, 配制成单一染料溶液, 分别将单一染料放入搭建的实验平台, 每隔30 s读取一次, 重复读取20次。 对于任一单一染料, 每次读数均可得到所有通道荧光检测数据。 采用前述提出的方法, 处理实验得到的各通道数据, 可得到荧光补偿矩阵。

2.4 多重颜色分辨实验

由于无法得到不同浓度染料的理论荧光值, 因此在多种染料混合测试时, 评价染料的串扰程度比较困难。 设计了一组颜色分辨实验来验证前述算法结果的准确性。 为了保证每各染料浓度都有相同机会接受测试, 而不受试验人员主观倾向的影响, 采用随机方式将不同浓度的多种染料进行组合测试, 将得到的数据进行荧光补偿后, 评价各染料荧光的线性度。 在PCR管中以盲法分析5种染料的混合物, 5种染料分别取各自线性范围内的6个浓度, 浓度从大到小依次编号1—6, 随机混合12组混合染料, 染料溶液混合方式由Matlab随机数发生器确定, 具体混合见表3, 每种混合方式对测试平台是未知的。

表3 染料随机组合表

3 结果与讨论

3.1 补偿矩阵的计算结果

检测结果如图4(a—e)所示, 分别表示用FAM、 HEX、 ROX、 Cy5和Cy5.5单一染料进行测试时, 各通道测得的荧光数据, 其中横坐标为相对应染料的荧光值, 纵坐标为其余通道的荧光值, 图中数据已被去除荧光背景。

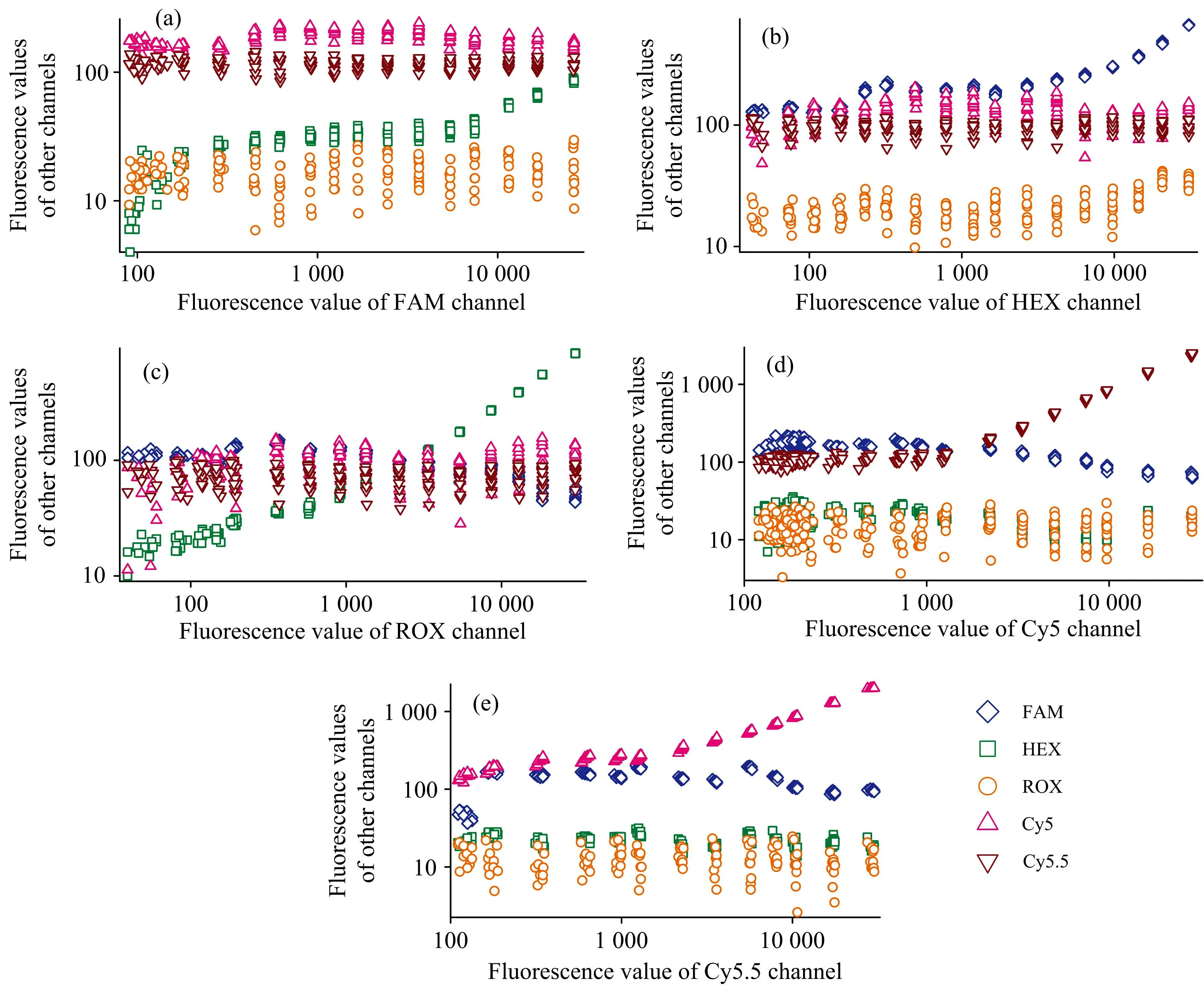
图4 不同浓度染料在各个通道的测试结果

从图4(b)中可以看出, HEX染料对FAM通道、 ROX染料对HEX通道、 Cy5染料对Cy5.5通道、 Cy5.5通道对Cy5通道分别有明显的干扰, FAM染料对HEX通道有轻微的串扰, 其余通道无明显的串扰。 另外, 从图中可以看出随着染料浓度的降低, 受干扰通道的线性度降低, 这是由于低浓度时, 受干扰通道接受到的光信号较弱, 超出了系统可检测的线性范围。 这种非线性对于荧光补偿来说是不利的, 但由于荧光值本身较小, 对检测影响不大。 个别浓度荧光值横轴间距不一致, 此外, 在低浓度时, 检测结果聚集成团, 推测是由于手动配制染料及实验误差所导致。

利用主成分分析方法, 获得荧光补偿矩阵见式(2)。

(2)

实验过程中, 由于系统误差带来的数据波动, 导致串扰矩阵中部分元素出现负数, 但理论上, 不应产生负串扰, 因此, 将负值设为0, 并对矩阵的每一列重新归一化, 得到新的串扰矩阵见式(3)。

(3)

观察串扰矩阵发现, Cy5通道对Cy5.5通道串扰较大, 串扰比例为8.76%, 意味着当仅采用Cy5染料进行实验时, Cy5.5通道也可检测到Cy5通道数值约8.76%的荧光值; 同样, Cy5.5通道对Cy5通道串扰影响也相对较大, 比例约为6.2%; 其次是ROX通道对HEX通道串扰, 比例约为2.68%; HEX通道对FAM通道串扰, 比例约为1.58%; FAM通道对HEX通道串扰相对较小, 比例约为0.25%, 其余通道无明显串扰。 与图4显示结果一致。

3.2 单一染料荧光补偿结果

将图4中测试数据R, 代入式(1), 进行荧光补偿计算, 得到染料的理论荧光值F, 以同样的方式绘制各通道数据, 如图5(a—e)所示。

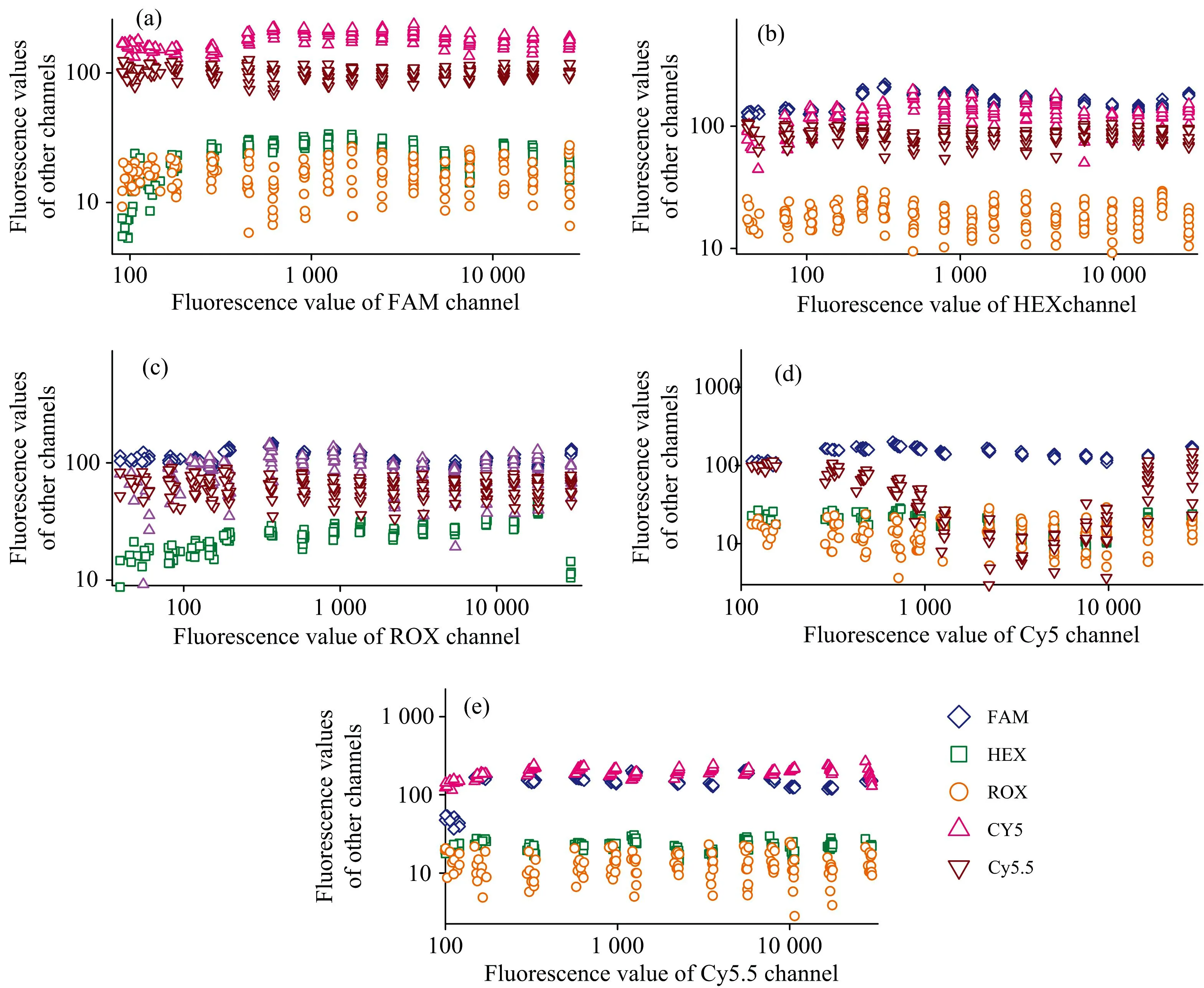
图5 经过串扰补偿后不同浓度染料在各个通道的分布情况

由图5(a—e)中可以看出, 经过补偿之后, 非目标通道的数据基本呈水平状态, 对各个通道分别进行线性拟合, 斜率最大为10-8, 趋近于零, 即非目标通道数值不随目标通道染料荧光值的上升而变化, 实现了荧光通道间串扰的解耦。

3.3 多重颜色分辨实验结果

荧光补偿矩阵与测试平台硬件及染料特性具有密切相关性, 当测试平台和染料荧光特性不变, 通过单一染料实验获得的补偿矩阵, 同样适用于多重染料的情况。 将不同浓度混合的染料放入搭建的实验平台, 分别进行实验, 将得到的测试结果代入前述补偿矩阵, 测得各染料浓度柱状图见图6。

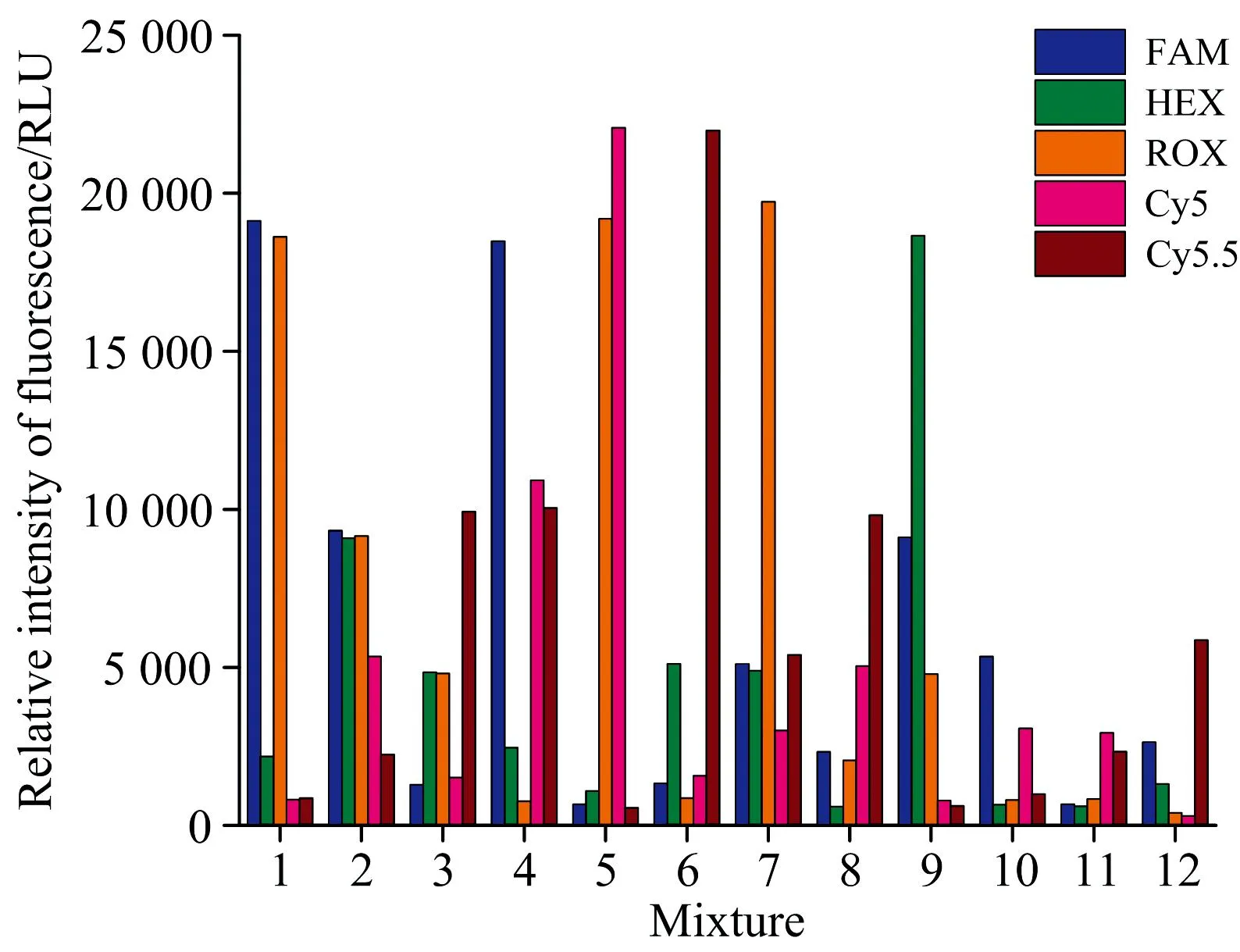
图6 混合染料的测试数据

对比观察表3和图6发现, 同一浓度的同一染料, 在不同的混合组合中, 荧光值相差不大, 没有受到其他通道的明显干扰。 从图4(d)中可知, Cy5染料对Cy5.5通道有明显的串扰, 表3中组合5和组合9里Cy5染料的浓度相差较大, 而两组中Cy5.5染料浓度较低且为同一值, 由图6看出, 经过补偿补偿后, 无论Cy5的染料浓度多大, Cy5.5的荧光值基本不受影响。 另外, ROX对HEX有明显串扰, 在组合5和组合12中, HEX浓度均为同一低值, 但ROX浓度相差较大, 但从图6可以看出, 两个组合中, HEX染料的荧光值基本一致, 未受到明显的干扰。 补偿算法有效地去除了染料间的干扰。

对各混合物中测得的不同浓度染料按照浓度大小进行了排序, 并取对数。 由图7看出, 对同一染料的不同浓度梯度进行拟合, 最大线性相关系数为0.999 3, 采用该算法, 能够很好地对染料的原始荧光进行区分。

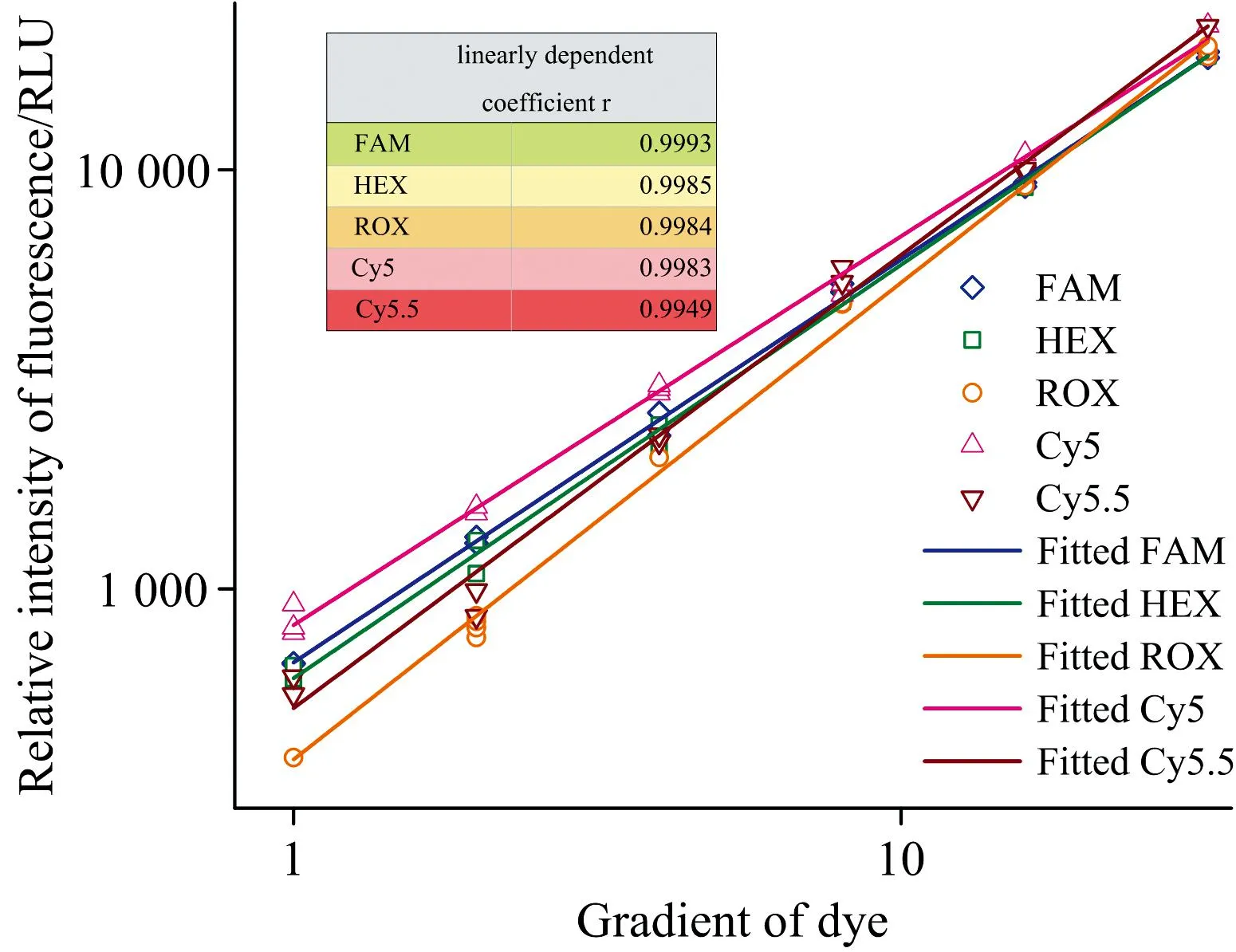
图7 各染料梯度的线性拟合

4 结 论

光谱重叠现象广泛存在于荧光定量PCR等多种荧光检测领域, 对检测结果带来不利影响。 本工作提出将主成分分析中求解主成分向量的计算方法, 应用到荧光定量PCR系统中, 该方法无需经过迭代计算, 即可获得系统的荧光补偿矩阵。 经过该矩阵的转换, 能够非常有效地分离各个荧光通道数据。 设计了染料分辨实验, 通过对随机组合的6个不同浓度的5种染料混合物进行实验测试和分析, 从中高效地分离了各个染料成分及其浓度, 进一步验证了方法的有效性。 本方法不受通道数量限制, 不仅可用于荧光定量PCR系统的荧光补偿校正, 也可用于其他具有串扰问题的光谱分析, 具有较高的使用拓展性。