基于正交试验的粒子群优化算法对火焰原子吸收光谱法分析金元素参数的优化

王 鹏, 何 涛, 白金峰, 冯小娟, 寇少磊, 吕明超,赵 浩, 邓一荣, 范 慧, 甘黎明*

1. 中国地质调查局西安矿产资源调查中心, 陕西 西安 710100

2. 中国地质科学院地球物理地球化学勘查研究所, 河北 廊坊 065000

3. 广东省环境科学研究院, 广东 广州 510045

4. 安徽省农业科学院, 安徽 合肥 230031

引 言

中国自然资源部于年初启动新一轮战略性国内找矿行动, 将重要能源矿产资源的勘查和储备能力提升到了新的高度。 而金矿产资源作为国家经济和高科技特殊材料的重要保障, 体现出重要的经济价值和战略地位, 其检测分析技术对于金元素准确测定提出了更高的要求。 目前金矿石中金元素的分析方法主要有氢醌容量法和火试金重量法等传统方法、 泡沫塑料和活性炭富集等原子吸收光谱法, 其中传统的检测方法对于技术人员的要求过高、 测试环境严苛、 操作流程冗长且污染物较多, 而活性炭富集仪器法同样具有测试周期长、 成本较高等缺陷, 因而实验室通常会选择泡沫塑料富集原子吸收光谱法分析矿石中金元素的含量, 可以回避上述方法缺点的同时还具备抗干扰强、 稳定性好、 操作容易、 成本较低的优势。

正交试验设计是一种优化多要素和指标的科学试验方法, 按照正交设计原理从众多试验中选择典型性的代表组合试验, 在科学研究和生产中可以减少试验次数和成本却能够保证方法的可行性和有效性[1], 提高了试验效率, 解决了试验要素和性能指标的关系。 层次分析法(analytic hierarchy process, AHP)是一种系统分析与决策的多目标或多方案的方法, 可以科学地将复杂问题层层分解, 对其中的关键要素进行主观赋值分析[2]。 客观赋权法(criteria importance though intercrieria correlation, CRITIC)是一种基于要素指标、 实验数据的客观赋权法, 基于数据之间的相关性和波动性, 对要素的权重科学且客观的赋值[3]。 粒子群优化算法(particle swarm optimization, PSO)是一种模仿鸟兽等集群捕食行为的寻优模拟算法, 通过迭代计算确定粒子在空间分析中的最优解, 在多目标参数优化方面具有独特优势[4-5]。

然而泡塑吸附原子吸收光谱法测试金元素的试验环节中的试样重量、 焙烧时间、 王水浓度、 熔样时间、 泡塑处理方式、 振荡时间、 解脱液浓度、 解脱时间等要素对于准确测量结果都有影响, 因此基于正交设计原理可以快速建立正交试验方案, 根据专家经验和实践定性判断和定量计算要素权重, 结合试验数据结果计算要素的对比强度和变异系数, 并提出基于AHP-CRITIC混合加权算法, 确保客观性计算要素权重的同时兼顾主观赋值的必要[6-7]。 最后利用PSO算法对惯性权重和学习因子进行校正, 建立目标适应度函数, 优化算法流程, 通过MATLAB软件模拟粒子迭代过程最终确定试验要素最佳组合参数[8-9], 为地质矿产实验室分析矿石中金元素的方法提供新方法, 在国家新一轮地质找矿突破行动中贡献力量。

1 实验部分

1.1 仪器及参数

采用日本日立公司研发的原子吸收分光光度计Z-2000, 光源为空心阴极灯(衡水宁强光源有限公司), 波长为242.8 nm, 灯电流为7.5 mA, 测定信号为BKG校正, 信号以积分方式计算, 狭缝宽度1.3 nm。 采用标准燃烧器原子化装置, 设置燃气流量1.8 L·min-1、 助燃气压力160 kPa、 燃烧器高度7.5 mm, 数据采集时间2 s。 采用标准曲线法测定样品浓度。

1.2 试剂和材料

成都市科隆化学品有限公司生产的盐酸(1.19 g·mL-1)和硝酸(1.42 g·mL-1), 均为电子级纯。

天津市大茂化学试剂厂生产的硫脲和三氯化铁, 均为分析纯; 北京双峰创优设备制造商过滤的超纯水, 电阻率18.25 MΩ·cm; 市场上售卖的聚氨酯塑料泡沫, 50 cm×50 cm×1 cm。

中国地质科学院地球物理地球化学勘查研究所研制的含量不同的金矿石分析标准物质: GAu-15a (0.32±0.02) μg·g-1、 GAu-16b (1.10±0.02) μg·g-1、 GAu-17b (3.2±0.2) μg·g-1、 GAu-18b (10.4±0.2) μg·g-1、 GAu-19b (18.3±0.4) μg·g-1、 GAu-22a (5.72±0.22) μg·g-1; 国家有色金属及电子材料分析测试中心研制的单元素金标准溶液(1 000 μg·mL-1)标准号GSB 04-1715-2004。

1.3 样品制备

称取干燥的金矿石标准物质20.0 g置于50 mL瓷坩埚中, 按照顺序依次放入马弗炉中, 从低温升至680 ℃, 打开炉门进入空气后继续灼烧60 min, 自然冷却后依次取出。 将焙烧后的样品倒入锥形瓶中, 缓慢加入100 mL王水(1体积硝酸, 3体积盐酸, 4体积水, 现用现配)摇匀, 放置于电热板上加热至微沸状态60～120 min左右, 保持锥形瓶内溶液大约15 mL取下, 加水至100 mL自然冷却, 放入一块用5%稀盐酸处理过的聚氨酯泡沫塑料。 将锥形瓶置于往复式振荡器中33 min, 保持室温25 ℃, 然后从锥形瓶中倒出泡塑用自来水冲洗干净, 置于20 mL浓度为9.5 g·L-1硫脲解脱液体中, 在水浴锅中保持沸腾状态30 min, 最后从比色管中趁热取出泡塑, 自然冷却并沉淀溶液待测。

1.4 实验设计及流程

实验以3 μg·mL-1金标准溶液为检测对象, 根据长期工作经验确定火焰原子吸收光谱法分析金元素中的王水浓度、 振荡时间和硫脲浓度为实验要素, 测定结果的偏离误差为量化指标从而建立正交试验。 通过层次分析法和CRITIC法分别对实验要素进行权重分析, 建立混合加权算法并计算权重, 结合实验要素权重结果构建目标函数, 改进惯性权重和学习因子对粒子群算法进行优化寻找最优参数, 利用MATLAB软件模拟迭代过程确定最佳实验要素。 实验设计思路示意图如图1所示。

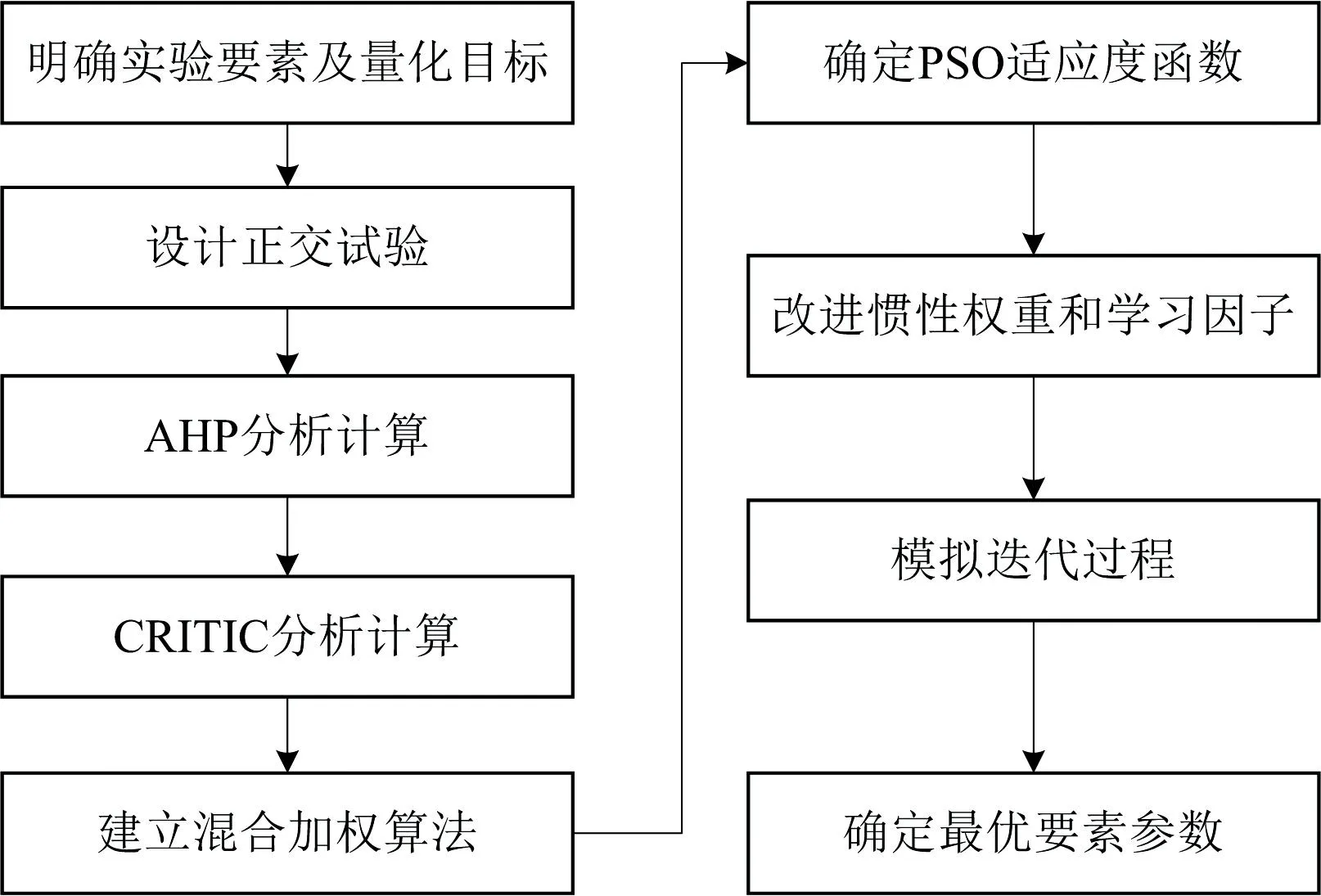
图1 实验设计思路示意图

2 结果与讨论

2.1 正交试验

多因素试验在科学研究和生产实践中至关重要, 通常需要进行不同因素的组合进行试验。 当试验中因素数量较少时, 能够进行所有可能组合的试验, 但是试验中因素数量较多时, 要完全覆盖可能的组合会产生较大的试验量, 极大程度影响试验效率。 因而通过正交理论和数学统计原理的正交试验法设计正交表, 可以合理缩小试验量、 节约时间和材料成本, 通过典型的代表性试验确保效果[10]。

试验目标是对3.0 μg·mL-1的金标准溶液准确测定, 以测量值的相对误差Δs为量化指标。 试验选择王水浓度x1、振荡时间x2和硫脲浓度x3为指标因素, 分别选取x1∈[0, 5, 10, 20]、x2∈[5, 15, 25, 35]、x3∈[0, 0.2, 0.5, 1]为水平范围, 设计三因素四水平的正交试验表L16(43), 试验结果如表1所示。

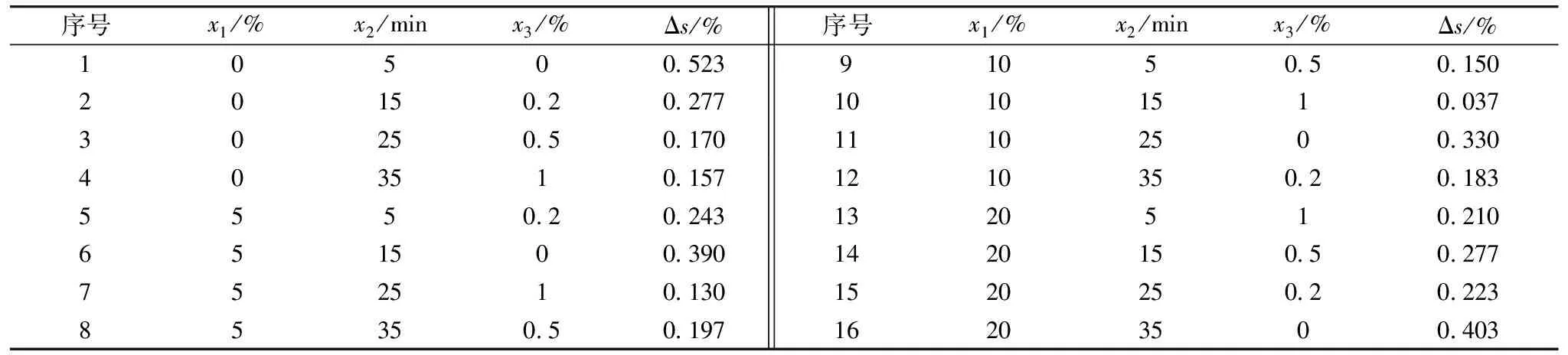
表1 正交试验结果表

2.2 AHP分析与计算

层次分析法可以优化处理定性判断与定量计算的过程, 通过主观判定要素之间的重要程度, 建立要素之间的判断矩阵将定性判断转化为可操作性的计算上, 擅于解决多要素、 多目标、 多层次的决策问题, 是计算各要素权重系数的重要手段。 实验中基于AHP分析各要素的具体步骤如下:

2.2.1 确定要素指标

实验在分析王水浓度x1、 振荡时间x2和硫脲浓度x3要素对火焰原子吸收法测定金元素的重要程度中, 在确保测定值偏离真实值越小的情况下, 设定其大小顺序为x3>x1>x2, 并采用1～5大小对要素间的比重进行量化, 1代表xi和xj相同重要; 5代表xi比xj非常重要; 2～4的标定同理可得。

2.2.2 建立判断矩阵

针对实验中的两两要素比较建立判断矩阵X,X必须满足xij>0、xii=1、xij=1/xji三个条件, 其中xij代表xi对xj的重要程度, 按照各要素指标间的重要程度及关系建立判断矩阵X如下

2.2.3 一致性判断

为了确保判断矩阵的准确性和合理性, 需要对X进行一致性判断, 用式(1)和式(2)计算

CR=CI/RI

(1)

CI=(λmax-m)/(m-1)

(2)

其中CR是一致性判断指标, 小于0.1即通过;CI是一致性判断指标;RI是与m对应的平均随机指标;λmax是X的最大特征根,m是X的阶数。

实验中计算λmax=3.054, 与之相应的特征向量ω=(0.756, 0.478, 1.767),m=3,RI=0.52, 计算CI=0.027,CR=0.052<0.1, 判断矩阵X具有良好的一致性[11]。

2.2.4 计算权重

矩阵X通过一致性判定后, 按照式(3)计算各要素指标的权重。

(3)

对矩阵X的特征向量ω归一化处理, 计算的权重结果ωAi=(0.252, 0.159.0.589)。

2.3 CRITIC分析与计算

CRITIC方法通常计算样本数据的标准差和变异系数来反映对比强度和冲突性的两个信息量, 该方法充分体现了数据之间的冲突性和差异性, 更加科学客观的推进赋权的过程。

2.3.1 指标标准化

根据正交试验数据可知, 各要素指标的量纲并不统一, 需要完成标准化计算。 通过Min-Max方法进行逆向指标计算

(4)

2.3.2 信息量计算

CRITIC赋权法中计算标准差反映各指标的对比强度[12], 其标准差si计算如式(5)所示

(5)

CRITIC赋权法中计算变异系数ρij表达冲突性, 计算公式如式(6)所示

ρij=cov(xi,xj)/(si,sj)

(6)

式(6)中, cov(xi,xj)代表实验数据中第i个和第j个要素指标的协方差。

各要素指标的信息量值越大, 表明该项指标越重要且权重更大, 通过计算vi和ρij可以表达该项指标的信息量, 计算公式如式(7)所示

(7)

2.3.3 计算组合权重

CRITIC赋权法通过冲突性和对比强度等指标的计算量进行权重赋值, 得到各要素指标的信息量后, CRITIC权重计算公式如式(8)所示

(8)

结合正交试验原始数据, 针对各项指标的不同水平量根据测定结果的相对误差的平均值作为评价指标进行归类, 通过CRITIC赋权法计算各要素指标的标准差、 冲突性和权重, 结果如表2所示。

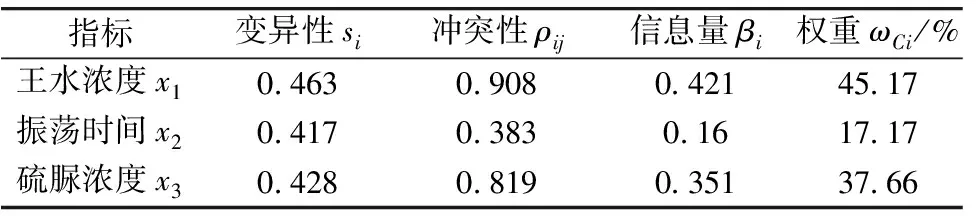
表2 CRITIC法计算权重结果表

从表2分析结果可知, 振荡时间的变异系数较小表明其波动较小, 影响测试结果的权重系数也较小; 王水浓度和硫脲浓度具有较强的冲突系数, 表明该项指标与振荡时间指标的相关性较弱, 可以作为较为独立的影响指标计算信息量, 因而所占有的权重系数较大。

2.3.4 建立混合加权算法

AHP法根据评价人员的经验主观判定各要素的权重指标, 体现出一定的主观局限性, 其可靠性和稳定性都难以得到确保。 CRITIC法依赖实验原始数据, 从数据本身研究各指标的信息量, 虽然科学计算且有据可循, 但无法兼顾数据之间的内在联系和实验之外的影响因素, 体现出一定的客观局限性[13]。 为体现实验数据权重的客观性和主观性, 提出AHP和CRITIC混合加权法, 使混合权重ωi偏离ωAi和ωCi尽可能小, 而不依靠其中一项, 根据最小信息鉴别原理建立目标函数

(9)

求解此目标函数, 计算混合权重ωi公式如式(10)所示

(10)

结合AHP权重赋值和CRITIC权重赋值, 计算最终混合权重ω=(0.314, 0.075, 0, 611)。

2.4 PSO算法优化

2.4.1 算法原理

粒子群优化算法可以完成复杂时间和空间中的要素搜索, 此方法具有寻优能力强、 收敛迅速、 和易于实现等特点。 PSO算法中每颗粒子具有速度和位置两个必须的属性, 分别代表粒子移动的快慢和方向。 每颗粒子在空间搜索中寻找最优解, 标记为此刻个体极值并共享与空间中的其他粒子群, 当粒子遍历完整个空间后根据当下的速度和位置不断更新, 最终找寻到空间最优解[14]。

2.4.2 求解流程

假设种群空间由N颗粒子构成D维空间, 每颗粒子i的移动只和速度和位置有关联, 分别用v和x表示, 用p表示粒子的局部最优和全局最优。 每颗粒子都要不断的迭代寻找最优解, 更新空间内的位置和速度, 计算公式如式(11)和式(12)所示

(11)

(12)

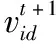
结合上述粒子位置变化推断, 所有粒子在寻优过程中只会向个体最优和全局最优的方向迭代, 在迭代过程中逐渐向同一个方向、 同一个位置靠近, 最终失去活性停止更新, 达到寻优的目的, 其具体的实现步骤如下:

(1)初始化参数: 设定种群大小、 维数、 随机函数r1和r2、c1和c2、 惯性权重、 迭代次数;

(2)建立适应度函数: 计算初始化粒子位置作为初始适应值fit(xi), 暂定为种群空间极值;

(3)更新粒子信息: 按照式(1)—式(3)不断更新速度和位置, 生产新的空间, 对边界进行检查;

(4)更新位置: 比较粒子当前位置和个体最优值、 全局最优值, 若非最优则继续迭代, 若当前位置更优, 则分别取代个体最优、 全局最优, 更新空间信息;

(5)判断结束: 若满足最大迭代次数, 则直接输出最佳参数组合, 否则t+1时刻的, 重新初始化进行。

PSO算法求解流程图如图2所示。

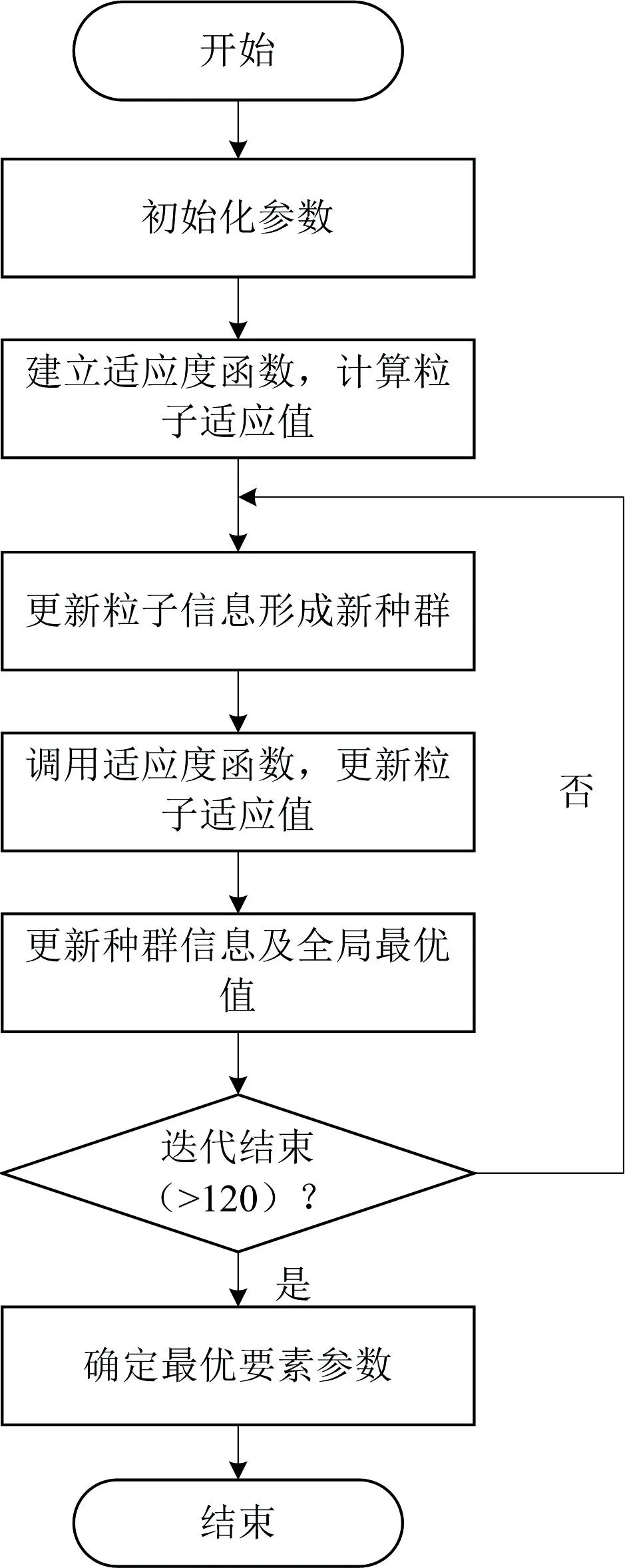
图2 PSO算法计算流程图

2.4.3 算法优化

PSO算法在寻找最优解的过程中容易陷入局部最优的循环中, 对于不同条件下的寻优不能确保每一次迭代向着全局最优靠拢, 通常对惯性权重ω和学习因子c进行改进, 提升算法的搜索效率和速度[15-16]。

研究表明惯性权重ω的大小对于PSO算法的搜索效能具有重要的影响,ω较大时能够改善粒子全局搜索的速度,ω较小时有利于算法的快速收敛。 为了确保算法全局搜索能力的同时又不会降低算法收敛的速度, 在迭代过程中通过线性递减的方式减小ω, 同时结合建立的组合权重ωi, 对改进后的惯性权重ω计算如式(13)所示

ωt=ωi(ωmin+(ωmax-ωmin)(t/T))

(13)

式(13)中,ωmax和是ωmin是最大和最小的惯性权重,t和T是当下的迭代次数和总迭代次数。

学习因子对于粒子在种群中的搜索方向有重要影响, 在粒子初始化全局迭代中,c2全局搜索能力更强, 而粒子的局部搜索能力较差, 应该确保此阶段迭代过程进行快速简单的搜索, 即确保c1较大,c2较小; 在迭代的最后时期粒子局部搜索能力更强, 搜索的重心在全局寻优中, 确保此阶段粒子精确的迭代搜索, 即确保c2较大,c1较小, 改进的学习因子计算公式如式(14)和式(15)所示

c1=cmin+(cmax-cmin)(1-t/T)

(14)

c2=cmax-(cmax-cmin)(1-t/T)

(15)

基于改进后的惯性权重和学习因子, 结合正交试验结果, 设计改进后优化算法的目标函数min[fit(x1,x2,x3)]。 采用第一组实验的参数组合作为算法的初始化, 最大迭代次数120次, 最大和最小惯性权重0.8和0.2, 使用MATLAB软件仿真算法实现, 得到粒子种群全局最优的迭代过程如图3所示。

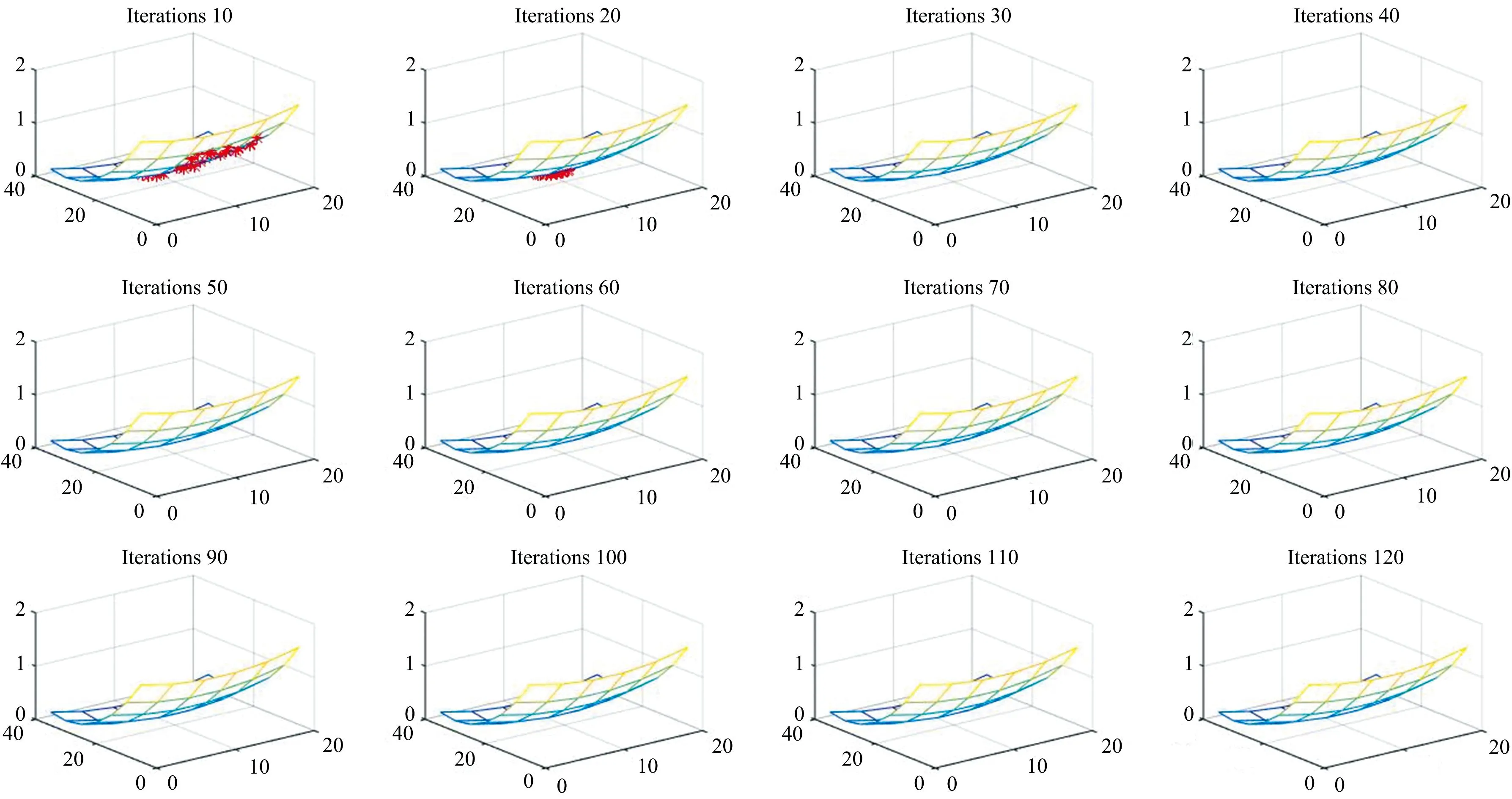
图3 PSO算法迭代过程示意图

通过图3迭代的过程可知, 粒子群通过迭代从全局各个位置逐渐向适应值收敛, 直至寻找到最优解(10.62, 32.8, 0.95)时, 算法结束, 即经过改进后的PSO算法寻求到火焰原子吸收分析金元素的最优条件解释王水浓度10.62%、 振荡时间32.8 min、 硫脲浓度9.5 g·L-1。

2.5 标准工作曲线绘制

按照粒子群优化算法寻找的最佳条件参数, 经过单元素金标准溶液逐级稀释配制标准工作曲线浓度分别为0、 0.5、 1、 2、 5、 10、 20 μg·mL-1, 以金空心阴极灯为光源、 火焰原子化装置为反应环境, 测定对应的吸光值。 同时以其质量浓度为横坐标建立标准工作曲线, 在0～20 μg·mL-1区间内与其吸光值具有良好的线性关系, 相关系数为0.999 9。

2.6 验证试验

按照1.3样品制备步骤对金矿中标准物质GAu-15a、 GAu-16b、 GAu-17b、 GAu-18b、 GAu-19b、 GAu-22a进行平行性试验, 其测定结果和标准值对比图如图4所示。

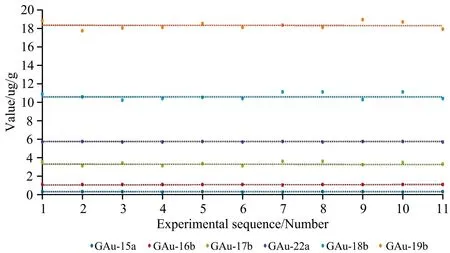
图4 金矿石标准物质测定值与标准值对比图

由图4分析可知, 标准物质的测定值均在其平均值周围波动, 按照《地质矿产实验室测试管理规范》计算其相对误差和相对标准偏差, 分别为6.5、 1.2、 4.9、 0.3、 2.7、 1.8和7.7、 1.7、 5.9、 0.5、 3.3、 2.1, 均小于贵金属标准物质化学分析的数学模型YB和YC, 分别为17.3、 11.9、 8.5、 7.2、 6.0、 5.1和24.4、 16.8、 12.1、 10.2、 8.5、 7.2。 由此表明, 基于正交试验的粒子群优化算法对金元素分析条件参数稳定可靠, 能够满足实验室分析测试的要求, 测试结果具有良好的稳定性和准确性, 能够为金矿产资源战略开发提供帮助。

3 结 论

为了在新一轮战略找矿行动中准确测定金矿产资源中金元素的含量, 根据正交设计原理对检测分析中的王水浓度、 振荡时间和硫脲浓度等实验要素建立正交试验。 结果表明: (1) 建立AHP-CRITIC混合加权算法计算实验要素权重结果为(0.314, 0.075, 0.611), 表明硫脲浓度要素影响权重最大, 可以作为较为独立的影响指标; (2) 采用粒子群优化算法对惯性权重和学习因子进行校正, 建立PSO算法优化流程, 通过MATLAB软件模拟粒子群迭代过程, 确定原子吸收光谱法测定金元素的最佳组合参数为王水浓度10.62%、 振荡时间32.8 min、 硫脲浓度9.5 g·L-1; (3)通过金矿石标准物质的验证试验, 测试结果的相对误差和相对标准偏差均满足《地质矿产实验室测试管理规范》。 此外, 该方法在地质矿产实验室的其他参数方法中还可以进一步优化改进, 有望在多目标参数寻优求解中提升速度和精度。