定向毫米波网络邻居发现协议

梁仕杰,赵海涛,张 姣,陈海涛,魏急波,王俊芳

(1. 中国电子科技集团公司 第五十四研究所, 河北 石家庄 050081; 2. 国防科技大学 电子科学学院, 湖南 长沙 410073)

随着5G移动通信、物联网与人工智能等技术的快速发展,增强/虚拟现实、自动驾驶、自然语言等新型资源密集型应用迅速占领移动互联网市场,这些应用往往需要进行高速率的连续采样与传输,对现有的通信资源提出了极大的挑战。毫米波具有大量可用频段,可作用于带宽密集型应用[1-3]。因此,近年来越来越多的研究人员将研究方向转向毫米波通信的研究。

毫米波通信的研究潜力巨大,但广泛的应用仍面临很多的挑战。毫米波通信的衰减要比S波段、C波段等低频段严重[4]。因此,一般要采用定向天线(相控阵天线)来对抗信号的高衰减特性,从而实现高速率的传输[5-6]。

在定向无线网络中,快速高效的邻居发现是个重要问题。目前,定向毫米波通信主要采用全向天线辅助进行邻居发现[7-9]。然而,全向天线的增益小于定向天线的增益,导致全向和定向的通信距离不同,因此采用全向天线辅助邻居发现的方法会导致某些邻居无法被发现。而且,基于全向天线辅助的方法还要求通信节点具备额外的全向射频模块。如何单纯利用节点已经具备的定向通信能力完成邻居发现就成为一个亟待解决的问题。

采用纯定向的邻居发现协议,可以分为随机类和确定类。随机类邻居发现算法[10-12]随机选择一个定向天线的波束指向方向,具有无记忆、平稳和健壮性的优势,可以用于没有任何先验信息和同步信息的环境中。但是,该算法得到的系统性能没有上界,导致其可能会需要非常长的邻居发现时间。确定类邻居发现协议[13-18]按照事先预定好的序列切换天线的方向或波束搜索方式实现波束交汇和邻居发现,有邻居发现时间的上界。

根据收发端时间的同步性,定向邻居发现协议还分为同步类邻居发现协议和异步类邻居发现协议。同步类邻居发现协议[19-20]需要收发双方的同步信息。异步类邻居发现协议[21-22]不需要双方的同步信息,但是发现时间会变长。

在定向的毫米波网络中,邻居发现阶段各个节点可能没有任何邻居交互信息。因此一个很重要的问题是如何在没有公共控制信道和任何先验信息的情况下发现邻居。定向通信的邻居发现需要收发双方的波束交汇,因此在没有公共控制信道和任何先验信息的条件下如何引导波束转向,实现收发双方的波束交汇是一个重要的课题。定向波束的邻居发现本质上是一个交汇(rendezvous)问题[23],当两节点的定向波束均指向对方并建立通信链路实现信号的发送与接收时,才可以实现邻居发现。在没有交互信息的情况下实现定向通信的邻居发现是一个盲交汇(blind rendezvous)问题[17-18, 23]。文献[17]提出了无协调定向邻居发现(oblivious directional neighbor discovery, ODND)协议,该协议能够在没有任何先验信息的条件下实现波束盲交汇并完成邻居发现,但问题是邻居发现时间较长。为了缩短ODND协议中的邻居发现时间,文献[18]进一步提出了基于连续扫描定向天线模型的波束盲交汇算法,并根据该算法设计出基于搜索的定向邻居发现(hunting-based directional neighbor discovery, HDND)协议实现邻居发现。然而,HDND协议的连续扫描定向天线模型较为理想,在工程中难以实现[24]。

本文提出了一种异步的确定性的基于盲交汇算法的邻居发现协议。该协议不需要任何交互信息,并且在首次基于盲交汇算法的邻居发现协议后执行基于位置预测的邻居发现协议来提高后续邻居发现速度,大量仿真实验验证了本文所提方法的有效性。

1 定向邻居发现盲交汇问题描述

邻居发现是实现网络媒体访问控制、拓扑控制等功能的关键技术之一。定向通信的邻居发现和全向通信的邻居发现不同,定向通信只能覆盖一个方位角,因此其邻居发现的复杂性远大于全向天线的邻居发现。在实际环境中,节点之间可能是异步的,邻居发现协议应该在没有公共控制信道和先验信息的情况下实现邻居发现。

定向通信邻居盲交汇问题定义为:在没有任何公共控制信道和先验信息,且没有任何时钟同步的情况下,实现有界的定向通信邻居发现。

1.1 系统模型

在一个二维毫米波定向通信网络中,每个节点配备定向天线,并且只在一个频段运行,每个天线可以切换方向到需要的位置。每个节点有N个(N为正整数)波束,忽略波束的切换时间,经过N次切换可以扫描所有的方向。每个波束的夹角为2π/N,当波束夹角为2π时,其退化成全向天线。

定向通信首先要保证发射端和接收端的波束交汇。为了便于说明,下面通过一个例子来描述定向通信波束交汇的过程,如图1所示。节点A和节点B均采用定向通信,它们均有6个波束,编号顺序按照逆时针编号,记为u={1,2,3,4,5,6},每个波束的夹角为π/3。节点A和节点B在彼此的定向-定向的通信范围内,彼此进行邻居发现需要双方波束同时指向对方(波束交汇)。

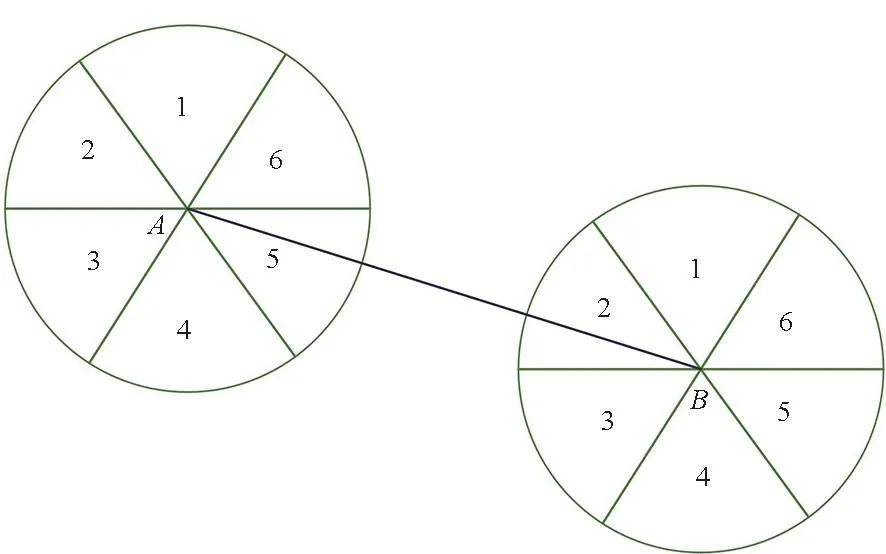
图1 天线波束模型Fig.1 Sectors of antenna model

假设节点A和节点B均按照逆时针方向旋转且时间同步,当前节点A指向波束4的方向记作PA=4,节点B指向波束3方向记作PB=3。假设节点A指向波束1,节点B指向波束4才能实现邻居发现,记作(dA-B=1,dB-A=4)。若节点A和节点B按照逆时针顺序切换下一个波束,根据PA、N可以得到节点A的扫描序列uA。根据PB、N可以得到节点B的扫描序列uB。

uA={4,5,6,1,2,3,4,5,6,1,2,3,…}

(1)

uB={3,4,5,6,1,2,3,4,5,6,1,2,…}

(2)

根据扫描序列uA和uB按照每个时隙切换一次,如图2所示。

图2 节点A和节点B波束扫描序列图Fig.2 Beam scan sequences of node A and node B

通过图2中的uA和uB可以得知:在这种情况下两个节点只能搜索出{(dA-B=1,dB-A=6)(dA-B=2,dB-A=1)(dA-B=3,dB-A=2)(dA-B=4,dB-A=3)(dA-B=5,dB-A=4)(dA-B=6,dB-A=5)}六组解,无法搜索到(dA-B=1,dB-A=4)这个解;无法实现节点A指向波束1同时节点B指向波束4,无法实现邻居发现。两个节点波束个数均为6时,共有36种交汇情况,因而无法搜索到所有解。

1.2 问题模型

在上述例子中,仍然存在一些无法完成波束交汇的情况。因此定向天线邻居发现盲交汇算法需要满足以下要求:

保证交汇:在有限的时间范围内,保证两个节点实现波束交汇。

全交汇:两个用户初始指向任何方向、交汇方向为任意方向,都可以保证波束交汇。

异步交汇:收发双方不需要时钟同步,也可完成盲交汇。

交汇时间:波束交汇必须至少保持一个时隙T(假设收发节点完成一次邻居发现时间为T)才能实现邻居发现。

在毫米波网络中,节点可能是不断移动的,因此两个节点交汇的方向dA-B和dB-A可能是任意组合,即∀dA-B∈[1,N],dB-A∈[1,N],其初始波束的位置也是随机的,即∀PA∈[1,N],PB[1,N],ua表示节点A根据PA和N生成的序列,ub是节点B根据PB和N生成的序列,因此定向天线的盲交汇数学优化问题为:

minTbr

s.t.∀dA-B∈[1,N],dB-A∈[1,N], ∀PA∈[1,N],PB∈[1,N]

∃t≤Tbr,ua(t)=dA-B,ub(t)=dB-A

(3)

式(3)表示的意思是:通过设计节点A的扫描序列ua和节点B的扫描序列ub最小化全交汇时间,保证节点A和节点B当前任意波束指向的组合(PA,PB)∈[1,N]×[1,N],节点A和节点B波束交汇的组合(dA-B,dB-A)∈[1,N]×[1,N],可以使节点A和节点B在t≤Tbr时刻分别指向dA-B和dB-A从而实现节点A和节点B的波束交汇。

2 基于位置预测的邻居发现算法

2.1 定向波束盲交汇算法

受圆形钟表的时分速率不同但终会相交这一现象启发,文献[25]提出了一种信道跳变的盲交汇算法,解决了无先验频谱信息条件下的多信道接入与通信问题。基于该思想,本文提出了一种定向天线波束盲交汇算法,该算法的主要思想是收发两端无公共波束信息,但在周期性定向旋转过程中仍然会实现波束交汇。但是,波束盲交汇算法和信道盲交汇算法仍然存在不同之处。在信道盲交汇过程中两个节点可用信道相同,信道个数为P。信道盲交汇满足两个节点在同一时刻处于共同可用的任意一个信道中,也就是说在所有信道均可用的情况下共有P种解,即{(1,1),(2,2),(3,3),…,(P-1,P-1),(P,P)}。波束盲交汇指的是两个节点的波束必须指向对方,在该时刻只有(dA-B,dB-A)一个解。

两个节点按照逆时针的方向切换波束来扫描所有方向,设发送端在每个方向停留的时间为MTT,接收端在每个方向停留的时间为MRT。MT和MR为整数且互质,即gcd(MT,MR)=1。

定理1两个用户在进行波束交互时,两个节点完成一个周期搜索的时间为MTMRNT。在一个周期内,两个节点可以搜索完一次所有波束交汇的可能性,并在下一次搜索同时回到搜索初始波束位置。

证明:发射端经过MTNT时间完成一次所有方向的扫描。接收端经过MRNT完成所有方向的扫描。接收端和发射端扫描完所有方向,并到达共同扫描的初始位置时,发射端和接收端组成的系统实现了一个周期的扫描。那么该系统的一个周期为MTNT和MRNT的最小公倍数,即MTMRNT。

□

定理2在同步状态下,只有在(MT=1,MR=N)或(MT=N,MR=1)条件下才能在最短的时间内实现全交汇,最短全交汇时间为N2T,最小盲交汇时间的上界为N2T。

□

在1.1节列举的波束交汇场景中,若令(MT=2,MR=3),其波束扫描序列如图3所示,在这种情况下无法搜索到(dA-B=1,dB-A=4)。若令(MT=1,MR=6),其波束扫描示意图如图4所示,在时隙9就可以搜索到(dA-B=1,dB-A=4)的情况从而实现波束交汇。在图4中, 经过36个时隙的时间,(MT=1,MR=6)条件下可以遍历所有波束交汇,实现全交汇。该场景收发双方的波束个数为6,至少经过36T的时间才能实现全交汇,(MT=1,MR=6)时可以实现全交汇最短全交汇时间。

图3 N=6,(MT=2,MR=3)时节点A和 节点B波束扫描序列Fig.3 Beam scan sequence of node A and node B when N=6,(MT=2,MR=3)

图4 N=6,(MT=1,MR=6)时节点A和 节点B波束扫描序列Fig.4 Beam scan sequence of node A and node B when N=6,(MT=1,MR=6)

定理3在异步状态下,只有(MT=1,MR=N+1)或者(MT=N+1,MR=1)条件下才能在最短的时间内实现全交汇,最短全交汇时间为N(N+1)T,最小盲交汇时间的上界为N(N+1)T。

证明: 在同步状态下,在最小最大交汇时间内无法在异步状态下实现全交汇,这是因为一定会存在若干个情况由于持续时间小于T从而导致无法实现波束盲交汇。由于一个搜索周期为N2T,在N2T时间内有些情况搜索不到将会导致这些情况永远无法搜索到。在同步状态下(dA-B=1,dB-A=4)、(dA-B=3,dB-A=6)均可以搜索到并保持一个时隙,如图5所示。在异步状态下,(dA-B=1,dB-A=4)持续时间大于一个时隙,(dA-B=3,dB-A=6)持续时间小于一个时隙,无法实现异步状态下的全交汇,如图6所示。

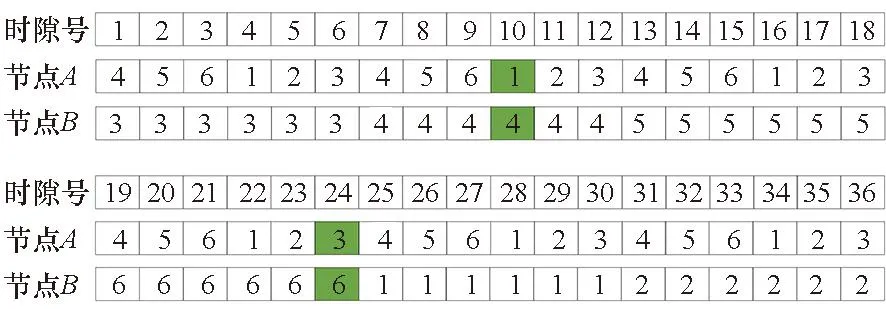
图5 同步状态且N=6时依据定理2 设计的波束扫描序列Fig.5 Beam scan sequence according to theorem 2 when the system is synchronous and N=6

□

令(MT=1,MR=N+1)或(MT=N+1,MR=1),节点A搜索完毕所有方向后,节点B在节点A的每个方向持续时间均大于T。因此,盲交汇消耗时间为N(N+1)T。在定理2中,在(MT≠1,MR≠N)或者(MT≠N,MR≠1)条件下,最短全交汇时间为min(MT,MR)·NT+N2T,在异步状态下最短全交汇时间至少为min(MT,MR)·NT+N2T。由于min(MT,MR)·NT+N2T大于N(N+1)T,因此在异步状态下,(MT=1,MR=N+1)或(MT=N+1,MR=1)条件下才能在最短的时间内实现全交汇,最短全交汇时间为N(N+1)T。在异步状态下,(MT=1,MR=N+1)或(MT=N+1,MR=1)条件下可以实现最小盲交汇时间的上界,最小盲交汇时间的上界为N(N+1)T。

在图7中,依据定理3设计的波束扫描序列可以搜索到(dA-B=3,dB-A=6)和(dA-B=1,dB-A=4)并保持一个时隙,改变了图6中某些异步状态搜索不到的情况。

图6 异步状态且N=6时依据定理2 设计的波束扫描序列Fig.6 Beam scan sequence according to theorem 2 when the system is asynchronous and N=6

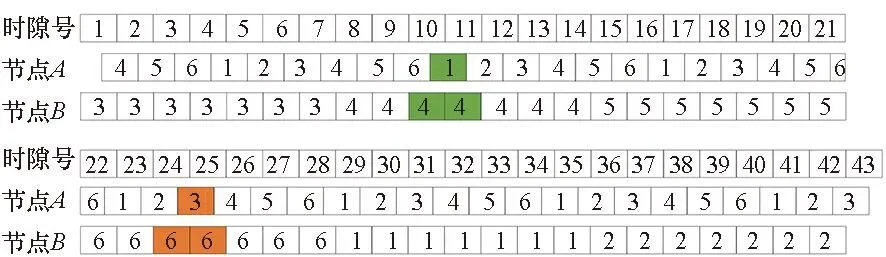
图7 异步状态且N=6时依据定理3 设计的波束扫描序列Fig.7 Beam scan sequence according to theorem 3 when the system is asynchronous and N=6

在两个节点进行波束交汇时,同步状态下盲交汇的最短时间为T,盲交汇的最长时间为N2T。因此,两个节点的同步状态下的盲交汇平均时间如式(4)所示,其中Z表示整数,i和j表示进行i次全方向搜索并在下一个全方向搜索j次可以实现波束交汇。

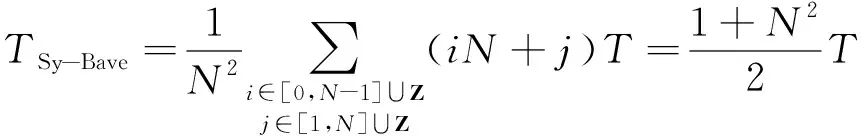
(4)

在异步状态下两个节点在进行波束交汇时,盲交汇最小时间为2T,盲交汇最大时间为N(N+1)T,因此在异步状态下的平均盲交汇时间如式(5)所示。

(5)

2.2 基于盲交汇算法的邻居发现协议

在利用2.1节实现波束交汇后,需要两个节点执行邻居发现协议实现邻居发现。

两个用户发射一个波束对准请求发送(beam alignment request to send, BARTS)的时间定义为TT-BARTS,接收一个波束对准允许发送(beam alignment clear to send, BACTS)的时间为TT-BACTS,将时间T定义为:

T≥2(TT-BARTS+TT-BACTS)

(6)

BARTS和BACTS数据包的数据结构如图8所示,其中Type表示帧类型,0表示控制帧,1表示数据帧;Subtype表示子类型,在这里表示BARTS数据包或者BACTS数据包;ID表示发射数据包节点的ID号;Location数据表示发射数据包节点从GPS导航中获取的位置信息;Time 表示发射数据包节点的时钟同步信息;Speed表示发射节点的速度信息;Direction表示当前该节点指向的方向。

图8 BARTS和BACTS结构Fig.8 Structure of BARTS and BACTS

2.3 基于位置预测的邻居发现协议

通过2.1节和2.2节的协议实现全网邻居发现后,每个节点可以发现本节点的邻居和本节点邻居的ID号、位置、速度、方向和时钟同步信息。

通过这些信息,可以加快后续节点的邻居发现,其中第i个用户的位置为(xi,yi),速度为vi,其运动方向与x轴正向的夹角为θi,节点发射上述信息的时间为ti。在tj时刻,节点j准备向节点i发射信息,此时节点i的位置表示为:

(7)

任意一个节点A在准备和其他用户B进行通信时,采用式(7)对其位置进行预测,直接对节点B的方向发射请求发送(request to send, RTS)数据包。RTS的数据包结构如图9所示。Type,Location,Time,Speed和Direction表示的含义与BARTS数据包也相同。Subtype在这里表示RTS数据包。Receive ID表示节点B的ID,Transmitter ID表示用户A的ID。Duration表示后续数据包需要的时间。

图9 RTS结构Fig.9 Structure of RTS

此时,节点A为发射状态,节点B为接收状态,双方就可以实现本次邻居发现。节点B最多进行N次波束切换就可以收到用户A的RTS数据包。在用户B接收到数据包后,可以获得用户A的位置速度方向时间信息。用户B采用式(7)计算用户A的位置,波束交汇用户A并发射允许发送(clear to send, CTS)数据包给用户A。CTS数据包结构如图10所示。

图10 CTS结构Fig.10 Structure of CTS

完成RTS/CTS邻居发现后,用户A进行数据传输。

基于预测的邻居发现协议的RTS和CTS结构比BARTS和BACTS结构长,增大了对信道的占用时间,但是预测算法减少了波束交汇时间,对信道的占用时间减少。基于位置预测算法的邻居发现协议与基于盲交汇算法的邻居发现协议的信道占用时间之比如式(8)所示,式中:TRTS,TCTS,TBARTS,TBACTS分别表示RTS,CTS,BARTS,BACTS时间;TP-BA表示基于预测算法邻居发现协议的平均邻居发现时间,如式(9)所示,其中i表示搜索次数。

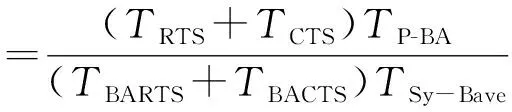
(8)

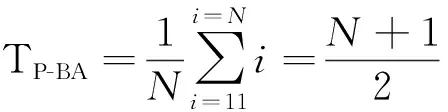
(9)

2.4 旁瓣效应下的邻居发现协议性能评估

前面所提出的盲交汇算法是基于理想的定向天线模型提出的。为了研究所提出的算法在更一般的场景中的适应性,对旁瓣效应下的邻居发现协议进行性能评估。

假设每个旁瓣的增益相同,主瓣和旁瓣的增益比为M。主瓣的增益为G(θ),因此天线增益模型[18]如式(10)所示,φ表示通信指向方向,θmain表示主瓣方向。

(10)

理想的单波束定向天线和考虑旁瓣的单波束定向天线的区别在于:在旁瓣可以覆盖的通信距离范围内,旁瓣可以发送和接收控制信息。因此可以提高邻居发现的效率,同时也会增大碰撞的可能。在这里不考虑碰撞,仅分析旁瓣增加邻居发现的效率。

旁瓣对于邻居发现的影响:

1)主瓣-旁瓣通信实现邻居发现;

2)旁瓣-旁瓣通信实现邻居发现。

在情况1的条件下,主瓣-主瓣同样也可以实现邻居发现,在情况2的条件下,主瓣-主瓣、主瓣-旁瓣也可以实现邻居发现。

2.4.1 主瓣-旁瓣通信实现邻居发现

当两个节点的主瓣-旁瓣之间的通信距离可以满足两个节点的通信距离需求时,可以提高邻居发现的速度。

在同步状态下,最大盲交汇时间为NT,因此其平均盲交汇时间如式(11)所示,i表示搜索次数。

在异步状态下,最大盲交汇时间为(N+1)T,因此平均盲交汇时间为:

2.4.2 旁瓣-旁瓣通信实现邻居发现

当两个节点的旁瓣-旁瓣之间的通信距离可以满足两个节点的通信距离需求时,可以提高邻居发现的速度。

旁瓣-旁瓣邻居情况下,邻居发现可以看作是全向天线的邻居发现,其同步异步状态均相同。因此其最长的盲交汇时间为T。

3 仿真分析

3.1 盲交汇算法计算复杂度性能对比

本节对本文所提盲交汇算法和文献[17]提出的ODND波束盲交汇算法的复杂度进行对比。这里将一个取余运算作为算法复杂度计算的单位。

在文献[17]提出的ODND算法中,每个时隙要进行一次取余运算来计算其天线的指向方向,因此在最坏的情况下,其要进行Lmax{paqb,pbqa}次取余运算。本文提出的盲交汇算法不需要进行取余运算,只要按照设计的序列顺序进行下次的天线选择即可。位置预测算法会增加算法运行时间,因此通过仿真分析盲交汇算法、位置预测算法和ODND算法计算复杂度。

采用MATLAB对三个算法进行算法复杂度仿真,设置仿真次数为10 000,统计算法的累计运行时间,结果如图11所示。

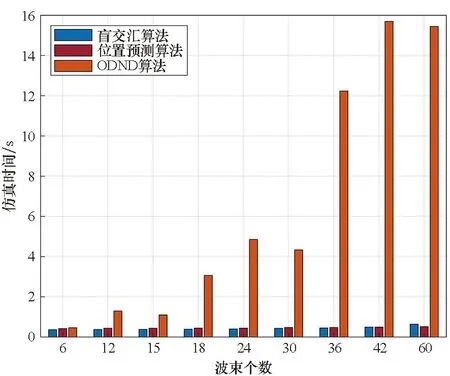
图11 不同算法复杂度对比Fig.11 Complexity comparison of different algorithms

图11可以看出,本文提出的盲交汇算法仿真时间远小于ODND算法,盲交汇算法的时间随波数个数增长而增长,并且不同的波束个数对应得到的仿真时间均小于ODND算法。ODND算法序列生成方式见文献[17]的式(2),根据该序列的生成方式可知:波束个数N接近满足式(13)的2n时,ODND协议的随机性大大降低,算法执行较少的选择语句,造成ODND算法的时间没有随着波速个数的增加而增加。波束个数为12的仿真时间大于波束个数为15的,波束个数为24的仿真时间大于波束个数为30的。但是其仿真时间均大于本文提出的算法。此外,位置预测算法增加位置预测会加大算法计算时间,因此在波束个数小于42时,位置预测算法的计算时间大于盲交汇算法。位置预测算法的解空间大小是N,而盲交汇算法和ODND算法的解空间是N2,随着N增大,解空间指数倍增大导致其计算时间增加速度远大于位置预测算法,在波束个数大于42时,其计算时间大于位置预测算法。

2n-11,n∈Z

(13)

3.2 基于盲交汇算法的邻居发现协议最长邻居 发现时间和平均邻居发现时间性能对比

为了验证盲交汇算法的邻居发现性能,对盲交汇算法邻居发现的最长发现时间和平均发现时间进行了仿真,并和文献[17]的ODND算法进行了对比。设置仿真次数为10 000,统计10 000次邻居发现的最长发现时间和10 000次邻居发现的平均发现时间。

不同算法的邻居发现协议最长邻居发现时间(时隙个数)如图12所示。从图12中可以看出,在不同波束个数条件下,基于盲交汇算法的邻居发现协议最长邻居发现时间均小于ODND协议的最长邻居发现时间。

图12 不同算法最长邻居发现时间对比Fig.12 Worst-case neighbor discovery delay comparison of different algorithms

不同算法的平均邻居发现时间(时隙个数)如图13所示。在波束个数为15、24、30、60时,基于盲交汇算法的邻居发现协议的平均发现时间小于ODND协议,其他情况下,基于盲交汇算法的邻居发现协议的平均发现时间大于ODND协议。由于波束个数N接近满足式(13)的2n时,ODND协议的随机性大大降低,其平均发现时间高于本文所提算法的。当节点波束个数N和满足式(13)的2n之差越大时,其随机发现的次数增加,从而降低了平均发现时间。若ODND算法的N仅满足2n≥N,可以通过增大2n减少平均邻居发现时间,但这会严重增加最长邻居发现时间。

图13 不同算法平均邻居发现时间对比Fig.13 Average neighbor discovery delay comparison of different algorithms

从图13中可以看出,在波束个数N接近满足式(13)的2n时,基于盲交汇算法的邻居发现协议的平均发现时间小于ODND协议。例如:N为12时基于盲交汇算法的邻居发现协议的平均发现时间大于ODND协议,当N为15时基于盲交汇算法的邻居发现协议的平均发现时间小于ODND协议。N为12和N为15时,符合式(13)的2n为16,因此当N接近16时,基于盲交汇算法的邻居发现协议的平均发现时间小于ODND协议。

为了对上述分析的结论进行更详细的说明,对基于盲交汇算法的邻居发现协议和ODND协议的平均发现时间进行对比。考虑波束个数为8～16和波束个数为16～32情况下,基于盲交汇算法的邻居发现协议和ODND协议得到的平均发现时间如图14和图15所示。

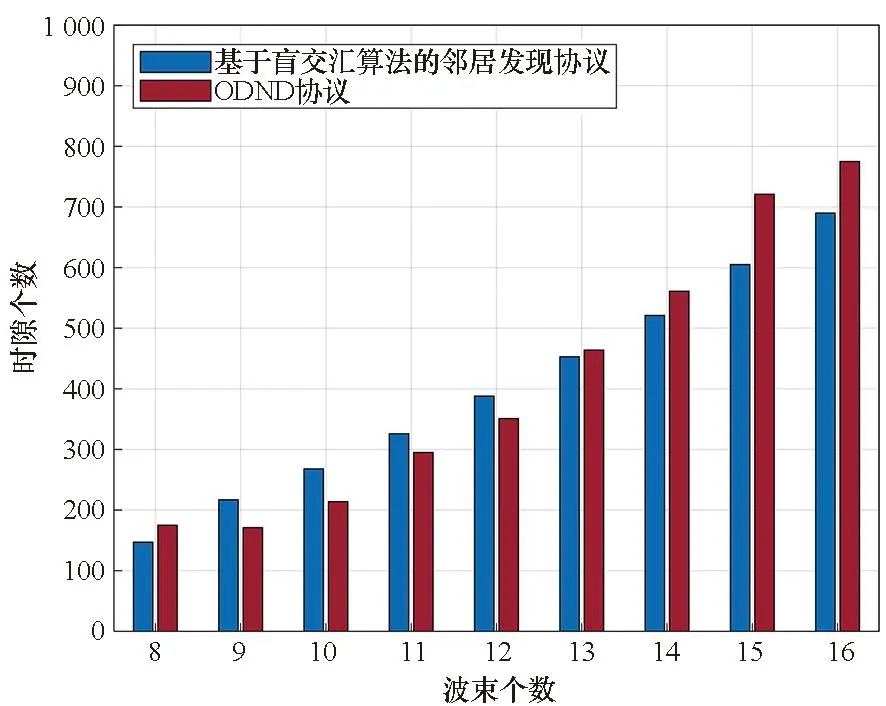
图14 波束个数为8到16时的平均发现时间对比Fig.14 Average discovery delay comparison under different number of sectors ranging from 8 to 16

从图14得知,在波束个数为8时基于盲交汇算法的邻居发现协议平均发现时间小于ODND协议,在波束个数为9时基于盲交汇算法的邻居发现协议平均发现时间大于ODND协议。这是因为在N为8时满足式(13)的2n为8,N和2n之差为0,由于ODND算法的随机性下降,基于盲交汇算法的邻居发现协议平均发现时间小于ODND算法。N为9时满足式(13)的2n为16,N和2n之差为7,基于盲交汇算法的邻居发现协议平均发现时间大于ODND算法。当波束个数大于等于13时满足式(13)的2n为16,N接近2n(16),基于盲交汇算法的邻居发现协议平均发现时间小于ODND协议。图15中可以得到相同的结论,在波束个数大于等于24时,N接近2n(32),基于盲交汇算法的邻居发现协议平均发现时间小于ODND协议。

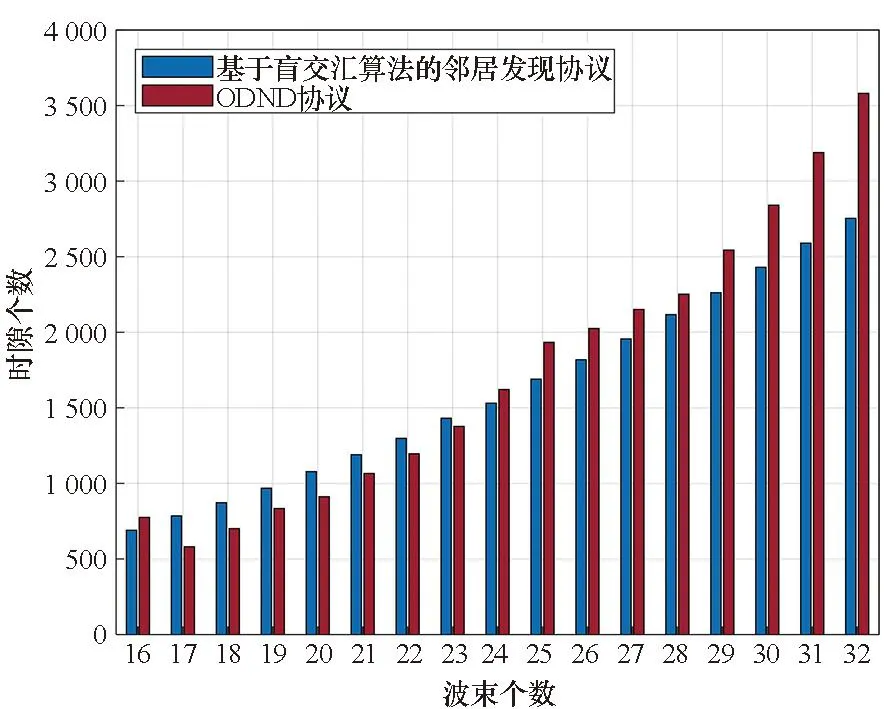
图15 波束个数为16到32时的平均发现时间对比Fig.15 Average discovery delay comparison under different number of sectors ranging from 16 to 32

3.3 基于位置预测的邻居发现算法性能

为了分析位置预测对邻居发现算法性能的影响,对比了采用位置预测和不采用位置预测情况下的邻居发现时间。令每对节点邻居发现100次,每次邻居发现后两个节点按照匀速直线运动,然后重新进行邻居发现。设置仿真实验次数为10 000,并取10 000次实验的平均值作为邻居发现的时间,结果如图16所示。

在图16中,通过对比不同波束下的邻居发现时间可以得知,基于位置预测后邻居发现的平均时间明显减小。在基于盲交汇算法的邻居发现协议首次邻居发现后,获得时间同步、位置、速度等信息,基于位置预测的邻居发现协议利用这些信息进行位置预测可以迅速降低邻居发现的时间。

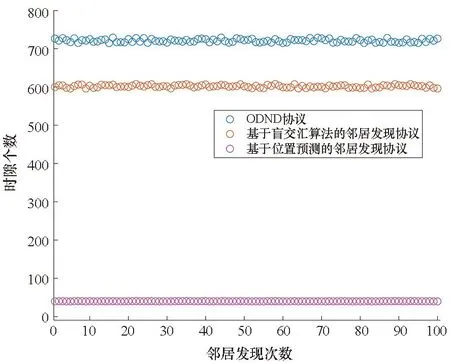
(a) 波束个数为15(a) Number of sectors is 15

(b) 波束个数为30(b) Number of sectors is 30

4 结论

本文提出了一种基于盲交汇算法的毫米波网络邻居发现协议。通过推导邻居发现过程中扫描间隔、波束个数与邻居发现时间之间的理论关系,提出了一种定向波束盲交汇算法。在没有任何交汇信息的情况下,两个节点通过基于盲交汇算法的邻居发现协议实现邻居发现。基于盲交汇算法的邻居发现协议只需按照波束盲交汇算法顺序扫描实现波束交汇,每个波束扫描时隙执行邻居发现协议便可以实现邻居发现。仿真验证得知基于盲交汇算法的邻居发现协议最长邻居发现时间小于ODND协议。各个节点通过基于盲交汇算法的邻居发现协议获得邻居位置、时间同步信息等信息后采用位置预测算法快速实现邻居发现。仿真验证结果表明,采用位置预测的算法后,邻居发现时间迅速减少。