基于气动方程的列车管路充排气数学模型

应之丁， 范 琳， 周和超

（同济大学 铁道与城市轨道交通研究院，上海，201804）

列车技术的发展对制动性能提出了更高的要求，需要进行新制动阀的研制或者对现有制动阀进行改进，并进行不同编组列车制动性能的测试和验证，以满足制动性能需求。传统的制动特性定置试验和线路试验，不仅耗时耗力，得到的试验数据十分离散。此外，在试验台上进行的验证性试验，不仅需要大量的新阀和更换制动阀，而且难以达到对新型制动系统做出预测的目的，成本高，周期长。通过理论推导的方式，建立整个编组列车的气压变化传递规律数学方程，很难满足精度要求，也很难将各种复杂的工况考虑全面。

基于小编组实物制动系统的前提下，考虑将首车模型数据曲线作为控制的目标曲线，输入到小编组实物制动系统的首车中，利用小编组的循环级联得到大编组列车的列车管气压变化数据，重点研究列车制动管路气压变化传递规律，进而研究大编组列车的制动性能。将首车模型与小编组实物制动系统试验数据相结合，从而建立半实物智能化仿真试验系统，实现对大编组列车制动系统性能的预测。其中不同编组列车首车列车管压力控制数学模型作为连接虚拟列车制动系统与后部车辆实物制动系统的接口控制关键软件，其列车管初充气及常用制动工况下的控制模型准确性，对整个编组列车控制模型的准确性具有决定作用。

国内外多个专业团队针对列车的控制模型及仿真试验做出了相关研究，并取得了一定的成果。文献[1］基于列车空气制动系统简洁有规律的气压传递管路，建立了列车制动系统半实物仿真平台及空气制动模型：文献[2］利用AMESim软件仿真分析了列车在不同工况下的制动性能；文献[3］建立了车辆系统、制动系统和控制策略的多系统协同分析平台；文献[4］建立了基于环境的列车制动模型，并提出了相应的制动模型辨识方法；文献[5］建立了气制动与纵向动力学集成系统的气制动系统模型，解决了列车纵向动力学研究中气制动力的激励和输入问题；文献[6］建立的制动模型综合考虑了空气黏度、传热等空气波现象。

本文从气动系统流体力学基本原理入手，建立了不同编组列车首车列车管的气路气容充排气数学模型，以初充气为例，该模型既考虑了风源向首车列车管充气，同时也考虑到了空气经过首车列车管继续向后传递的过程。同时引入修正系数对将除首车之外的其余车辆的列车管看作一个气容时，由于列车管横截面积小，长度大的形状特征所带来的计算偏差进行修正。并且提出通过对阀有效截面积的设计计算，并带入所建立的数学模型中进行仿真试验，从而对研制新制动阀及改进或检修制动阀提供理论基础与技术指导。

1 气动系统流体力学原理

1.1 完全气体状态方程

在外界条件的变化下，系统内的气体能够极快的建立一系列的新的平衡状态。在平衡状态下，完全气体的压力、体积和温度三个量间的数学关系，叫做完全气体状态方程。实际制动系统管路气态方程非常复杂，难以解析并应用于实时控制，为寻找管路气压传递规律，可以先利用完全气体假设推导首车列车管的充排气数学模型，此后根据试验数据规律做流体传递修正。

式中：p为绝对压强；V为体积；N为物质的量；R为气体常数，对空气有R=287N·m·(kg·K)－1；T为热力学温度。

1.2 质量流量方程

在dt时间内，充入容器内的气体质量为

式中：m1是充入容器内的气体质量；qm1是dt时间内流入容器的质量流量。

在dt时间内，从容器内放出的气体质量为

式中：m2是从容器内放出的气体质量；qm2是dt时间流出容器的质量流量。

当回路处于声速流动时，回路中通过的气体质量流量的计算公式为

式中：qm为回路中通过的气体质量流量，kg·s-1；P1为气动元件上游管道内的静压力（绝对压力），kPa；P2为气动元件下游管道内的静压力（绝对压力），kPa；T1为气动元件上游的总温，K；S为节流孔有效截面积，m2；b为临界压力比。对于一般气动元件，临界压力比b=0.2～0.5[7］。

当回路处于亚声速流动时，回路中通过的气体质量流量的计算公式为

1.3 有效截面积

1.3.1 制动阀的有效截面积

推导制动控制模型的目的之一是用于构建研制新制动阀与改进或检修制动阀的技术分析平台。通过利用几何面积合成法，计算阀的有效截面积（与阀体内部关键的进排气通路孔径和布置有关），并代入所推出的充排气数学模型中，从而分析阀的充排气性能，为以后阀的改进提供理论依据[8］。

式中：S0为阀的有效截面积；M为阀内节流口的数量；Ai为第i个节流口的面积，i=1，2，…M。

1.3.2 管路系统的合成有效截面积

气体流过复杂的气动元件时，其流动损失是不能忽略的。因流经空气管道的空气流受空气黏性的影响，所以与通过受黏性影响极小的小孔流动在各种情况下都不相似，但若附加上空气黏度来进行充排气时间等的计算，会使计算变得更加复杂，所以将管道换算成等价的小孔，即管道带来的气体流动损失也用有效截面积S来表示。S作为阀和管道总的有效截面积[9］。本研究中将首车列车管看作一个气容，其余车辆的列车管看作一个气容，所以风源向首车列车管充气时，管路系统的有效截面积是由风源到首车列车管之间的各类阀和管路的折算有效截面积。首车列车管向后部车辆充气时，管路系统的有效截面积即为首车列车管折算有效截面积。在实际管路中管道和阀是串联连接的，合成有效截面积由式（7）求得

式中：g为管道及阀的总数量；Sj为第j个管道或阀有效截面积，j=1，2，…g。

1.3.3 声速与亚声速条件下的有效截面积的关系

因为气体在不同的流态下，流过流道时产生的压力损失是不同的，而有效截面积正是用来表示器件内通道流通能力的物理量，所以即使是同一个元器件，在通过不同流态的气体时，其有效截面积也是不相等的，设亚声速流态下元件的有效截面积为A，声速流态下元件的有效截面积S，则两者有以下关系[10］

实际上A为不可压缩流态下的有效截面积，在这里近似为亚声速流态下的有效截面积。其中，节流阀口的理论有效截面积为30Πmm2[11］。

2 不同编组列车首车列车管的气路气容充排气数学模型

模拟不同编组列车制动系统试验，即利用气动方程推导的首车列车管传递规律模型控制不同编组列车的首车列车管压力，并结合制动系统试验台进行试验验证，修正每次小编组车辆循环级联压力控制模型，利用小编组实物车辆制动系统循环级联试验，实现多编组列车制动系统试验。

在此前的研究中[12］提出可将列车管简化为相应的等效风缸来对其压力变化进行研究，本文在此基础上，将编组列车的首车列车管看作一个气容，其余车辆的列车管看作一个气容。初充气时，每一时刻首车列车管内的压力为风源充入首车列车管内的压力减去首车列车管充入后部车辆列车管内的压力，制动工况下类似，提出以下不同编组列车首车列车管充排气数学模型。

2.1 首车列车管初充气工况模型

列车管充气初期阶段压力变化较快，各腔室和管路来不及与外界进行交换散热，故刚开始充气时接近绝热过程。随着气缸内压力增加，升压速度开始减慢，最后接近等温过程。由于试验测得充气时编组列车后部与首车列车管的压力比值大于b（b=0.5），所以认为首车向后部车辆列车管的充气过程为亚声速。

如图1 所示，压力为P1， 温度为T1的恒定的气源，经过有效截面积为S， 临界压力比为b的管路系统，向另一容积为V，初始压力为P20、初始温度为T20（设T20=T1）的容器内充气。

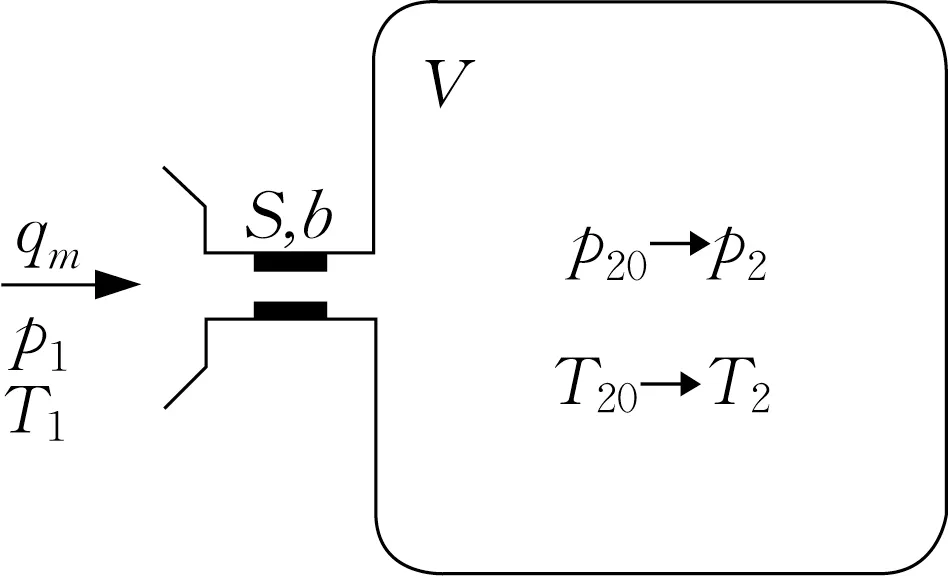
图1 充气过程Fig.1 Inflation process

由此得到充气时列车管的简化模型如图2所示，压力为P1， 温度为T1的恒定气源，经过管路系统，向首车列车管等效为的容积为为单车列车管主管长度、直径；L2、D2为单车列车管支管长度、直径）、初始压力为PL0、初始温度为TS0（设TS0=T1）的容器内充气，同时首车列车管等效为的气容，向后部车辆等效为的容积为为 列 车 编 组数）、初始压力为Ph0、初始温度为Th0（设Th0=T1）的容器内充气。

图2 充气时列车管简化模型Fig.2 Simplified model of train tube when inflating

2.1.1 首车列车管绝热充气阶段数学模型

对定容积的绝热充气，有[13］

其中，k为等熵指数，对空气，k=1.4。

由式（1）、（2）、（9）可得

声速充气时，即P2/P1≤b时，令式（4）与式（10）相等得容器由P20充至P2所需的充气时间为

亚声速充气时，即b＜P2/P1≤ 1时，令式（6）与式（10）相等得容器由P20充至P2所需的充气时间为

由式（11）、（12）可得向封闭容器绝热充气时，容器内压力与时间的关系为

由式（13）可得编组列车首车列车管绝热过程初充气的数学模型为

式中：W为长大列车管等效为一个气容时的等效系数；Sh为声速流态下由风源到首车列车管之间的各类阀和管路的折算有效截面积；Ac为首车列车管向其后车辆进行亚声速充气时的列车管折合有效截面积。

2.1.2 首车列车管等温充气阶段数学模型

等温充气即充气过程中，容器内的温度不变，即在图1中有T2=T20=T1。

将式（1）代入式（2）可得

同绝热充气段推导，可得声速与亚声速充气时，容器由P20充至P2所需的充气时间为

由式（16）可得向封闭容器等温充气时，容器内压力随时间的变化关系为

由式（17）可得编组列车首车列车管等温过程初充气的数学模型为

其中，Ah为亚声速流态下由风源到首车列车管之间的各类阀和管路的合成有效截面积。

2.2 首车列车管制动工况模型

与初充气工况类似，制动工况下的列车管排气也为先绝热排气，后等温排气的过程。后部车辆列车管向首车列车管的排气过程为亚声速过程。

如图3 所示，某一容器内的压力空气，经某气动元件或气动回路，向外界或另一容器放气。其中该容器的容积为V，初始压力为P10、初始温度为T10，气动元件的流量特性参数为S和b，气动元件下游的压力为P2，系统温度T10=T2。由此得到的列车管放气时的简化模型如图4所示。

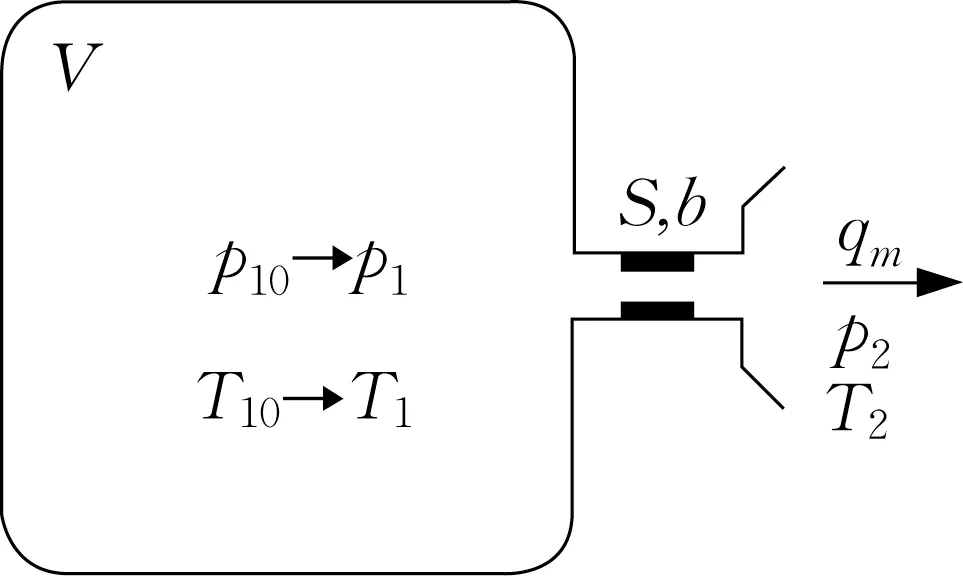
图3 放气过程Fig.3 Deflated process

图4 放气时列车管简化模型Fig.4 Simplified model of train tube when deflating

2.2.1 首车列车管绝热排气阶段数学模型

根据质量守恒定律和能量守恒定律，可得到绝热排气时，对定容积容器，满足[14］

由式（1）、（3）、（19）可得

同绝热充气阶段推导可得声速与亚声速放气时，容器由P10充至P1所需的排气时间为

其中，亚声速排气时，利用了亚声速绝热充气与等温充气的关系，将亚声速绝热排气时间表示为等温排气时间的1/k 倍，并利用修正系数Q（Q=22）进行了修正。

由式（21）得封闭容器绝热排气时，容器内压力随时间的变化关系为

由式（22）得编组列车首车列车管绝热排气时的数学模型为

由于不同制动级别下机车控制阀阀口控制流量不同，故引入阀口开度系数β，与声速条件下阀的有效截面积S0相乘，用于区别不同制动级别下的阀口控制流量.

引入编组差异系数γ，与后部车辆列车管向首车列车管排气时的列车管折合有效截面积Az相乘，表示除首车之外的后部车辆首车列车管向首车充气时由于编组数不同造成的气体损失量差异。

2.2.2 首车列车管等温排气段数学模型

与等温充气推导过程相同，可得在容器等温排气时，容器内的压力随时间变化的关系式为

由式（24）可得编组列车首车列车管等温排气过程的数学模型为

PL=

3 列车制动系统的仿真分析

为验证本文提出的首车列车管充排气模型的正确性，在中车某车辆有限公司的列车制动性能试验台上进行了试验，试验台如图5所示，主要由150辆车的制动系统及管路和测试气压的传感器和排气电磁阀、带两台制动执行器半实物制动仿真测控系统组成，在试验台上进行试验测得50、75、150编组时的首车列车管初充气及1、7级制动时的气压数据。将试验采集得到的数据运用MATLAB绘制出曲线图，并将仿真模型计算所得的结果与其进行对比分析，以验证模型的正确性。

图5 试验装置图Fig.5 Test setup diagram

3.1 初充气工况验证

3.1.1 模型基本参数

首车列车管初充气工况模型的参数值列于表1，将参数值带入模型中，计算初充气工况下不同车辆编组列车首车列车管内压力变化情况，并绘制曲线与真实试验数据相比较。

表1 首车初充气模型参数表Tab.1 Parameter table of the initial inflation model of the first car

3.1.2 仿真结果与试验数据对比分析

初充气至定压500KPa 时，仿真曲线与试验曲线如图6所示。

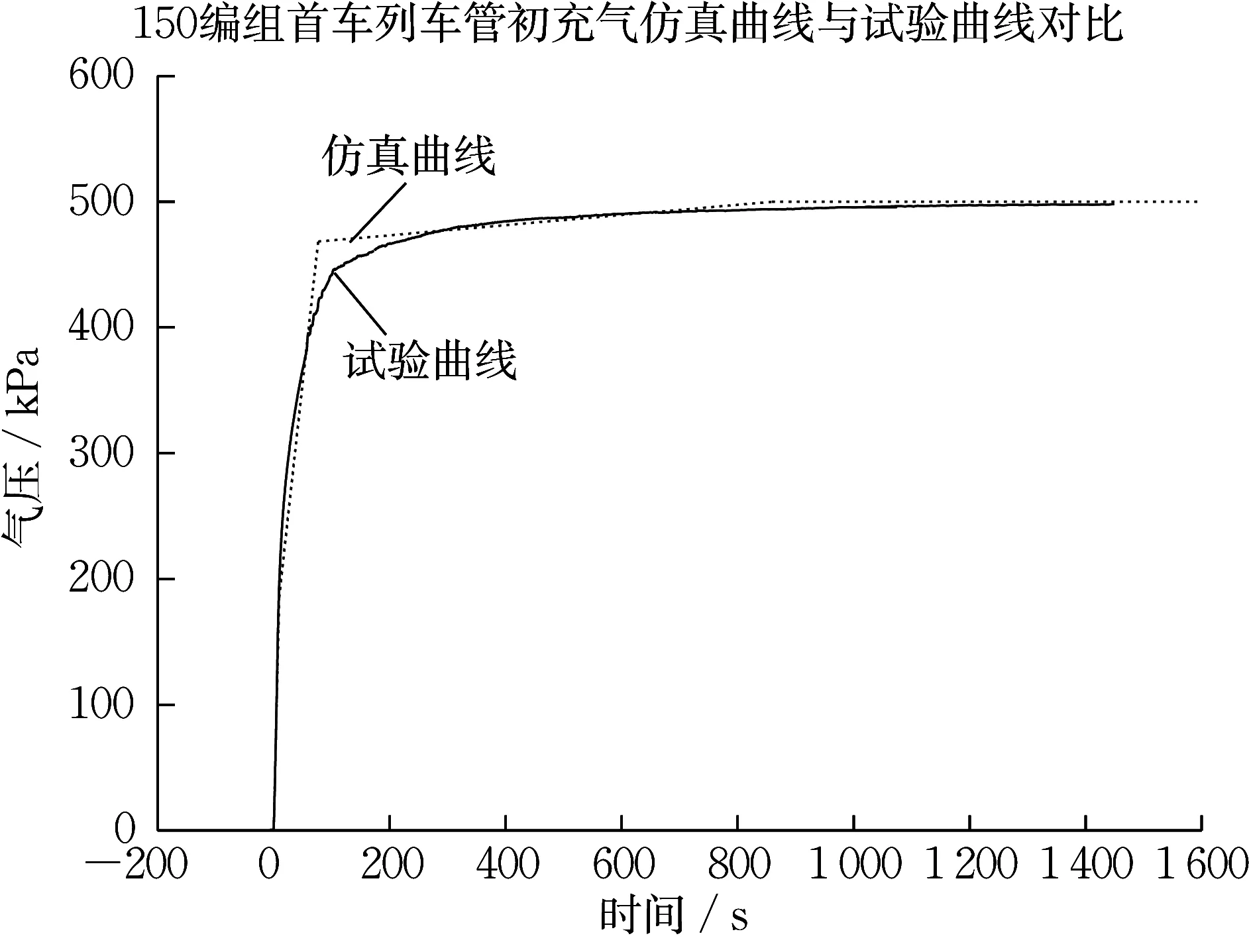
图6 初充气曲线Fig.6 Initial inflation curve

由图6可以看出，初充气工况的仿真结果和试验数据较为吻合，差异最大点在等温声速充气与亚声速充气的分段点，偏差大小为15.8%，在允许范围之内，仿真的正确性较好。

3.2 常用制动工况验证

3.2.1 模型基本参数

首车列车管常用制动工况模型的参数值列于表2，列车管长度、直径、温度、等效系数参数在表1中已列出。将参数值带入模型中，计算常用1级及7级制动工况下不同车辆编组列车首车列车管内压力变化情况，并绘制曲线与真实试验数据相比较。观察参数表可得同一制动级别下各编组的βS0、βA0值相同，γAz值与编组数成正比，由此可预测出200 编组常用制动时的模型参数列于表2。

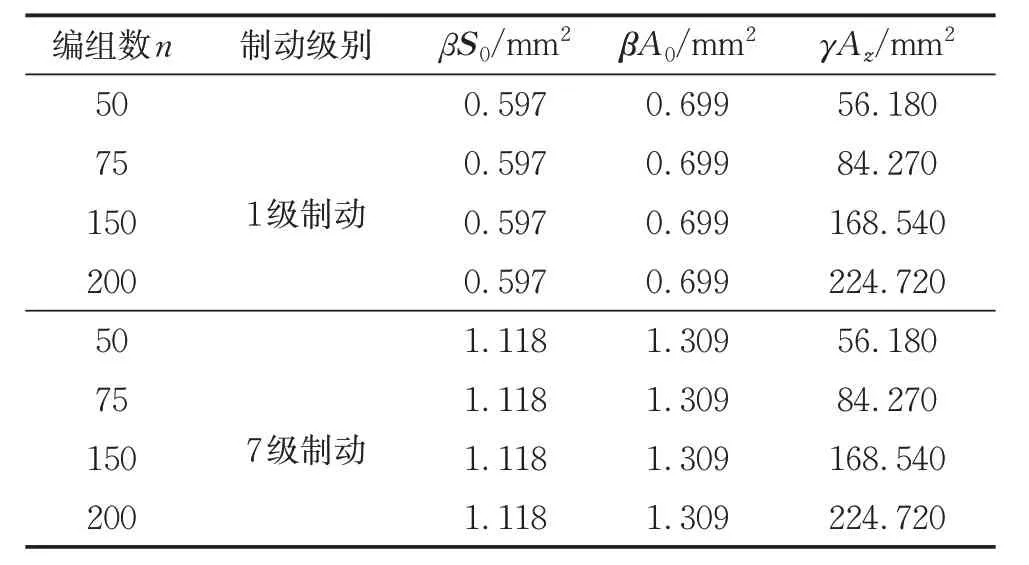
表2 首车制动模型参数Tab.2 Parameters of the first car braking model

3.2.2 仿真结果与试验数据对比分析

常用1 级制动及7 级制动时的仿真曲线与试验曲线如图7所示。

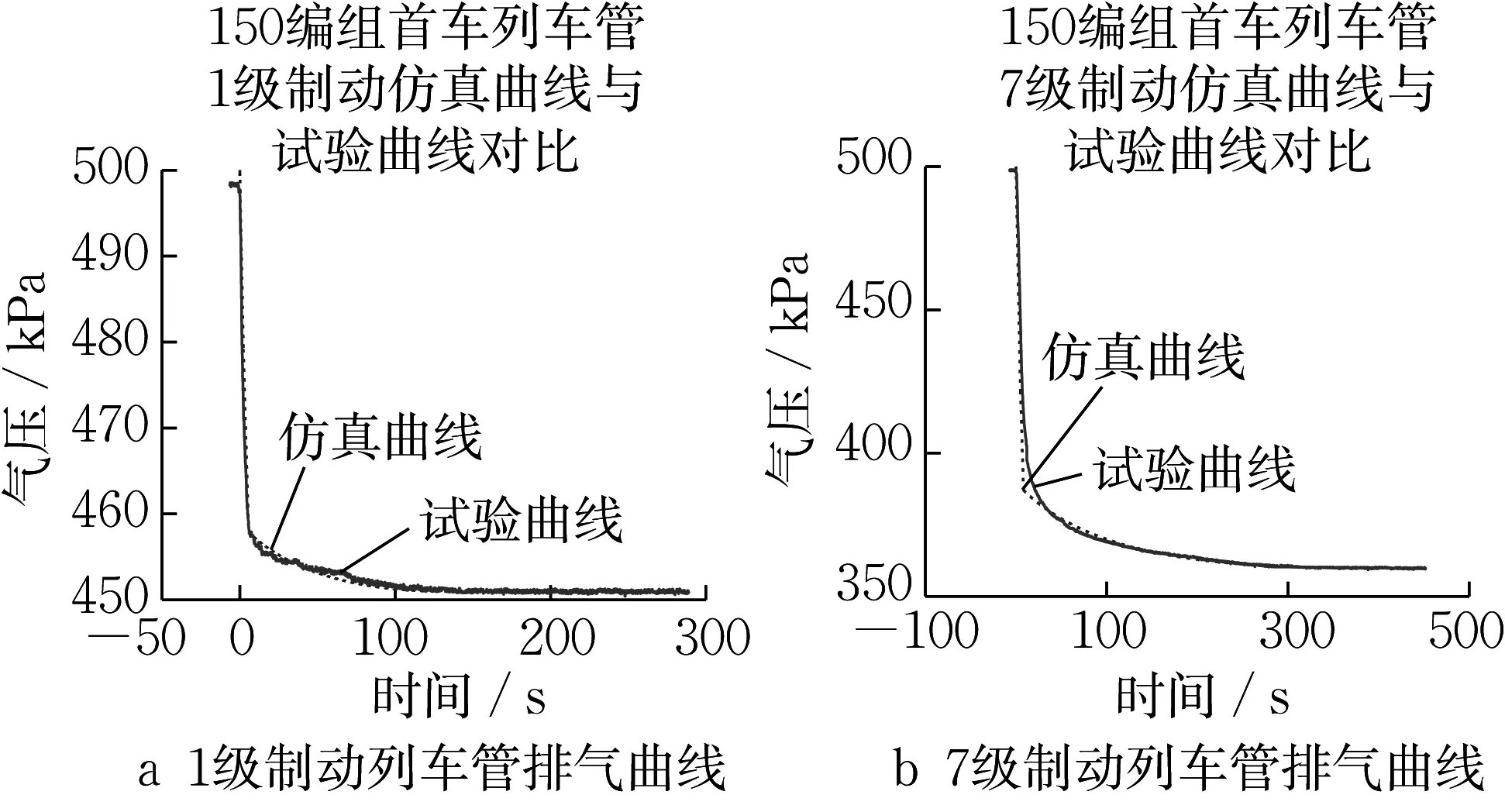
图7 制动工况列车管排气曲线Fig.7 Exhaust curve of train pipe under braking condition

由图7可以看出，1级制动时，仿真结果和试验数据差异最大点在绝热放气段，偏差大小为2.1%；7级制动时，差异最大点仍在等温声速充气与亚声速充气的分段点，偏差大小为9.3%，仿真的正确性较好。

3.3 更长编组首车列车管初充气及常用制动列车管压力预测

将表1、表2 列出的模型参数带入首车列车管充排气数学模型，令编组数为200，将所得数据绘制成曲线如图8。将200编组首车列车管充排气模型曲线作为控制目标曲线输入到试验台中，通过小编组实物制动系统循环级联便可得到200 编组列车初充气及制动时各车的列车管气压数据，从而分析列车制动性能。

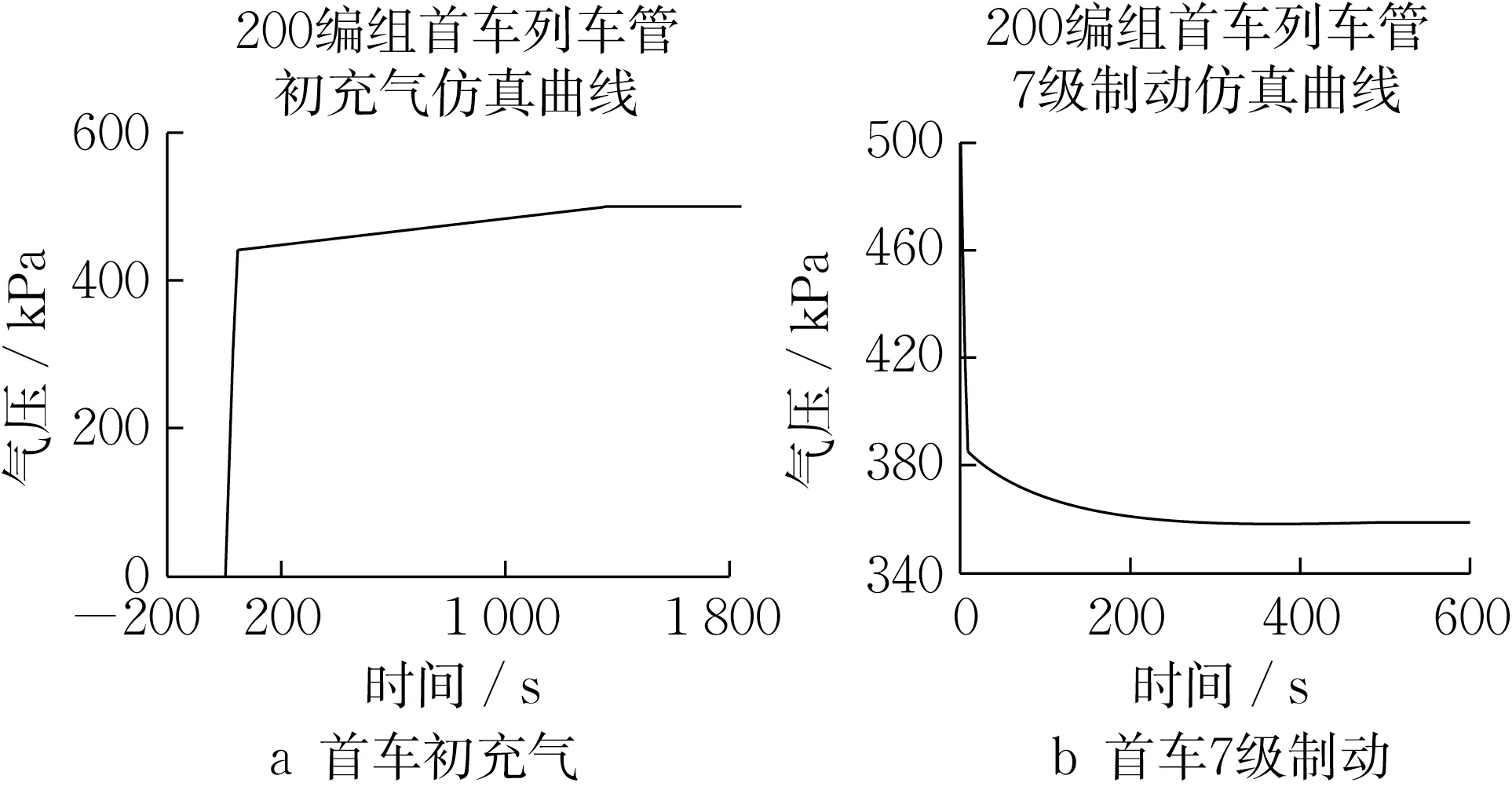
图8 列车管充排气曲线Fig.8 Charge and exhaust curve of the first train tube

4 结语

通过气动系统流体力学原理，建立不同编组列车首车列车管充排气时的压力变化模型，以初充气为例，该首车列车管模型既考虑了风源向首车列车管充气，同时也考虑到了空气经过首车列车管继续向后传递的过程，即得到了首车列车管实际充排气过程中的 “边充边排” 模型，理论上来说该模型更加准确。

本文提出通过计算或设计制动阀的有效截面积，进而带入推导出的首车列车管气路气容充排气数学模型中，根据模型数据结果分析制动阀的有效截面积对列车制动性能的影响，并通过试验研究不同制动级别下阀口的开度大小，从而为研制新制动阀及改进或修理制动阀提供技术分析平台。

利用列车制动系统智能化试验平台进行初充气及常用1级、7级制动试验，试验曲线与仿真曲线吻合程度较好，最大偏差为15.8%，分析其原因为实际音速临界常数b与理论值存在偏差，以及未通过试验测得实际阀的有效截面积、管路系统的合成有效截面积及不同制动级别下阀口开度大小，今后将根据试验测得更为准确的参数值。在今后的工作中也考虑加入修正曲线使曲线段得以平滑衔接。

作者贡献声明：

应之丁：提出研究思路，进行论文修订等工作；

范 琳：设计研究方案，进行试验、论文起草及修订等工作；

周和超：研究方案修改，论文修订等工作。