贫数据中基于模型自训练的空气处理设备故障诊断

孟 华， 裴 迪， 阮应君， 钱凡悦， 邓永康， 郑铭桦

（同济大学 机械与能源工程学院，上海 201804）

加强暖通空调（HVAC）系统、尤其是AHU的故障检测和诊断（FDD）研究对节能减排意义重大[1-2］。当前，HVAC FDD 的研究方法大致包括基于模型、基于知识和基于数据驱动3 类[3］，笔者检索了Web of Science 核心数据集2012―2021 十年间HVAC FDD 的研究文献共528 篇，基于数据驱动的文章占比从60%逐年提升至87%，该研究方法已成为主流。而无论从设备全寿命周期内故障率遵循的 “浴盆曲线” 看，还是从NASA对复杂设备所归纳的典型故障概率看，AHU 作为暖通空调中的常见设备，由于人工诊断故障成本高昂，致使其实际运行中的故障标签样本极少，即处于AHU FDD 贫数据情景。而近年来，在贫数据情景中针对历史运行故障数据的特征选择、提高模型诊断准确率等问题，已日益成为研究热点[4-5］。

在HVAC FDD的故障数据特征选择研究中，通常采用某种算法对重要特征进行筛选，以实现特征降维、提高计算速度并提升模型诊断性能。Han等[6］利用最大相关最小冗余及遗传算法包裹支持向量机（SVM）对冷水机组的特征子集进行特征选择，节省约63%～72%的计算时间。Yan 等[7-8］使用ReliefF算法从冷水机组65 个特征中筛选6 个典型特征，实现5 个故障90.31%的诊断准确率。Li 等[9］利用基于信息贪婪的特征滤波器剔除AHU 数据中的噪声和冗余特征，在不同的故障诊断模型上获得3.54%～25.29%的准确率提升。但是，目前研究尚较少有基于分类模型对不同算法最优特征子集的特性进行对比研究的，尤其是对在贫数据情景中不同算法性能稳定性等研究还很有限，而这些研究对优化HVAC FDD特征维度、提高计算速度及提升模型诊断准确率至关重要。

由于分类器性能往往随故障标签量的减少而降低[10-11］，在贫数据情景中，自训练算法能够利用少量故障标签样本训练分类模型，以故障伪标签扩充训练集，并提升模型性能。Yan等[12］开发SVM自训练模型用于贫数据时的AHU FDD，使其在少量故障标签下的诊断准确率提升到80%和90%以上。Fan等[13-14］将自训练神经网络模型用于AHU FDD，在不同学习率及置信阈值下，利用伪标签使诊断准确率最高提升约30%，并提高未知故障的检测率。尽管自训练算法对于贫数据情景很有效，但是，当前针对深层网络自训练的研究还较少，尤其是关于小故障样本量、或伪标签选取策略等问题对自训练模型准确率提升的效果影响等研究还较有限，而加强相关研究对提升贫数据时AHU FDD的诊断准确率大有裨益。

本文就4 种典型特征选择算法对于AHU 夏季运行故障标签匮乏情景的适用性及在不同特征子集维度下的性能及稳定性进行对比研究，甄选最优子集，针对贫数据提出将DBN 嵌入自训练框架的故障诊断模型，探究真实故障标签量及伪标签筛选策略对模型诊断性能的影响。

1 AHU FDD方法

1.1 特征选择

选择在机器学习领域典型数据集中表现良好的4种算法[15］，其计算成本低，通用性强，适于贫数据情景中AHU FDD故障数据特征降维。

（1）最大信息系数（MIC）。用于量化特征与故障的相关性，即

式中：X是特征向量；Y是故障标签；I[X；Y]是互信息值；i，j是对二维散点图的网格划分；网格分辨率限制常数B是样本量n的函数，B=n0.6。

（2）最大相关最小冗余（MRMR）。利用互信息量化特征子集的冗余度，如下

式中：S指特征子集的维度；D(S，c)指特征子集中每个特征与故障互信息的和；R(S)指子集中特征之间的互信息之和。

（3）ReliefF 的逻辑是惩罚样本的类内差异并奖励类间差异，以此量化特征对分类的影响。特征权重W(Fi)及样本在特征分量下的差异diff分别为

式中：样本总量为m；X为所有样本中随机抽取的样本；A、B为故障类别；从两类故障样本中各抽取k个与X最邻近的样本，样本Xi与X故障类别相同；Xj为不同类故障样本；P(A)为A故障出现的概率。

（4）ILFS. 它是基于图的特征选择算法，以计算特征xi中元素的Fisher 分数并量子化进行特征降维。其邻接矩阵A储存的特征关联ai，j=φ(xi，xj)由概率潜在语义分析的变体技术自动赋值，按照无限特征选择（Inf-FS）计算冗余性。

1.2 DBN自训练模型

选择DBN[16］为AHU FDD 的分类模型，它是一种深度学习网络，通过叠加多个受限的玻尔兹曼机构建显、隐两层结构。先利用不包含故障信息的数据初步生成网络节点参数，再利用数据故障标签对整个网络参数进行调整。DBN 模型最大的优点是能够有效提取数据深层特征，当输入的特征子集维度较小时可保持良好的诊断性能，模型训练时间短，适于自训练这种需要大量迭代训练的半监督方法。

自训练算法[17］原理为：设有L种故障，含故障标签的数据集为X={(xn，yn)，n=1，2，…，N}，故障标签为yn∈{1，2，…，L}，无故障标签的数据集为U={um，m=1，2，…，M}。自训练的每一次迭代包含两步，第一步根据故障标签样本训练得到 “教师” 模型，第二步由教师模型利用无标签样本um生成伪标 签m，得 到 伪 标 签 数 据 集={(um，)，m=1，2，…，M}，由筛选策略选择含有高质量伪标签的样本集∈，扩充训练集得到X′=X∪。本文所提出的DBN 自训练算法用于AHU FDD 的故障诊断流程见图1。其中 “是否满足退出条件” 的具体解释见2.3.1。

图1 基于特征选择及DBN自训练的AHU FDD流程图Fig. 1 AHU FDD flow chart based on feature selection and DBN self-training model

1.3 评价指标

采用三项指标对模型诊断性能进行评价

式中：TP为正确分类阳性样本；TN为正确分类阴性样本；FN为将阳性样本错分为阴性；FP代表将阴性样本错分为阳性样本。上述评价指标对二分类及多故障的诊断情景都适用。

2 AHU故障诊断实例分析

2.1 数据来源及处理

数据集来自ASHRAE AHU 夏季故障实验（PR-1 312）[18-20］，其既包含不同类型的AHU 故障，例如新/排风阀卡死、冷却盘管阀门控制失稳、AHU管道泄漏等；还包含AHU 同类故障的不同等级，例如对于 “冷却盘管阀门卡死” 故障，共有阀门全关、阀门开度15%、阀门开度65%及阀门全开4 种故障等级。该数据集共包括19 种工况，18 种故障及1 种正常状态，稳态工况时每种699个数据样本，有效样本总数为13281。通过手动剔除实验数据中诸如故障控制信号、实验启停布尔逻辑信号等无关特征后，共获得80 个有效特征。利用拉伊达准则剔除特征向量异常值并标准化，得到数据的合理分布。随机抽取总样本的70%为训练集、其余30%为测试集，各数据集中不同工况均匀分布。

2.2 特征选择

为探究对比MRMR、ReliefF、MIC 和ILFS 这4种特征选择算法在贫数据情景中的性能，各算法中的参数设定依次为：初始子集维度取1，K邻近数为10，网格分辨率限制常数取样本量的0.6次方，特征量子化维度为6。取贫数据样本容量为总样本的5%（665 个）；为消除随机性，样本集随机抽样5 次，诊断结果取平均。

采用4种特征选择算法分别计算80个有效特征与AHU故障标签之间的量化相关性并降序排列，得出4个降序列队，分别取各列队中的前N个值，得到维度为N的特征子集，由该子集包含的特征值分别训练DBN 模型，得到4 种算法在不同特征子集维度N时的DBN FDD故障诊断准确率，见图2，由于4种算法在模型训练中的耗时相差很小，故以4 种算法的平均耗时由图2中的虚线给出。所用DBN模型的参数均经大量仿真实验确定，具体见表1。

表1 DBN模型的参数设置Tab. 1 Parameters for DBN model

图2 4种算法在不同维度N时的DBN FDD诊断准确率及模型平均训练耗时Fig. 2 DBN FDD accuracy for MRMR, ReliefF,ILFS, MIC and their average training time at different N

由图2 可见，4 种不同特征排列的DBN FDD 准确率均随维度N的增加而升高，这说明随着更多特征的加入，更多的故障信息被DBN 模型学习；但当N超过20 后，FDD 准确率上升趋势趋于平缓，说明特征数量的增加对诊断准确率提升产生边际效应，但训练计算耗时却显著增加。因此，若综合考虑诊断准确率和模型计算量，可取最佳特征子集维度N为20。如图2，将4 种特征选择算法的性能进行对比，可见除MRMR 外，当维度N低于10 时，ReliefF准确率较好、计算耗时也较低，性能较好，但当N高于15时，MIC性能超过ReliefF与ILFS；而在全部特征子集维度N中，MRMR的性能始终最佳。

为进一步探究对比4种特征选择算法在贫数据情景时相对于其在充足数据（13 281个）样本时的性能稳定性，现将其分别应用于充足样本情景，得到各自的理想特征排列。取子集维度N为20，对比4 种算法选择的特征子集在贫数据情景下与理想情况下所包含特征元素的差异，图3给出4种算法的特征子集的稳定性可视化对比，图中D1～D5分别表示五次不同随机抽样产生的5%样本量的贫数据集，白色方框表示各算法在贫数据及数据充足的情景下都能筛选得到的特征，灰色方框表示各算法在各次随机抽样时与理想子集的特征差异，由图可见，MRMR几乎不受样本数量的影响，其在贫数据条件下筛选的特征子集与理想情况最多相差1 个特征，甚至在D4 随机实验中的贫数据特征能完全代表理想特征子集；而MIC和ReliefF的特征稳定性差异达到2～3个，ILFS最不稳定，差异特征数达到8～14个。由此可见，在4种特征选择算法中，MRMR在贫数据时的诊断性能及子集元素稳定性均最优，因此本文后续将由MRMR 选取的前20 个特征作为模型训练及测试的输入特征。

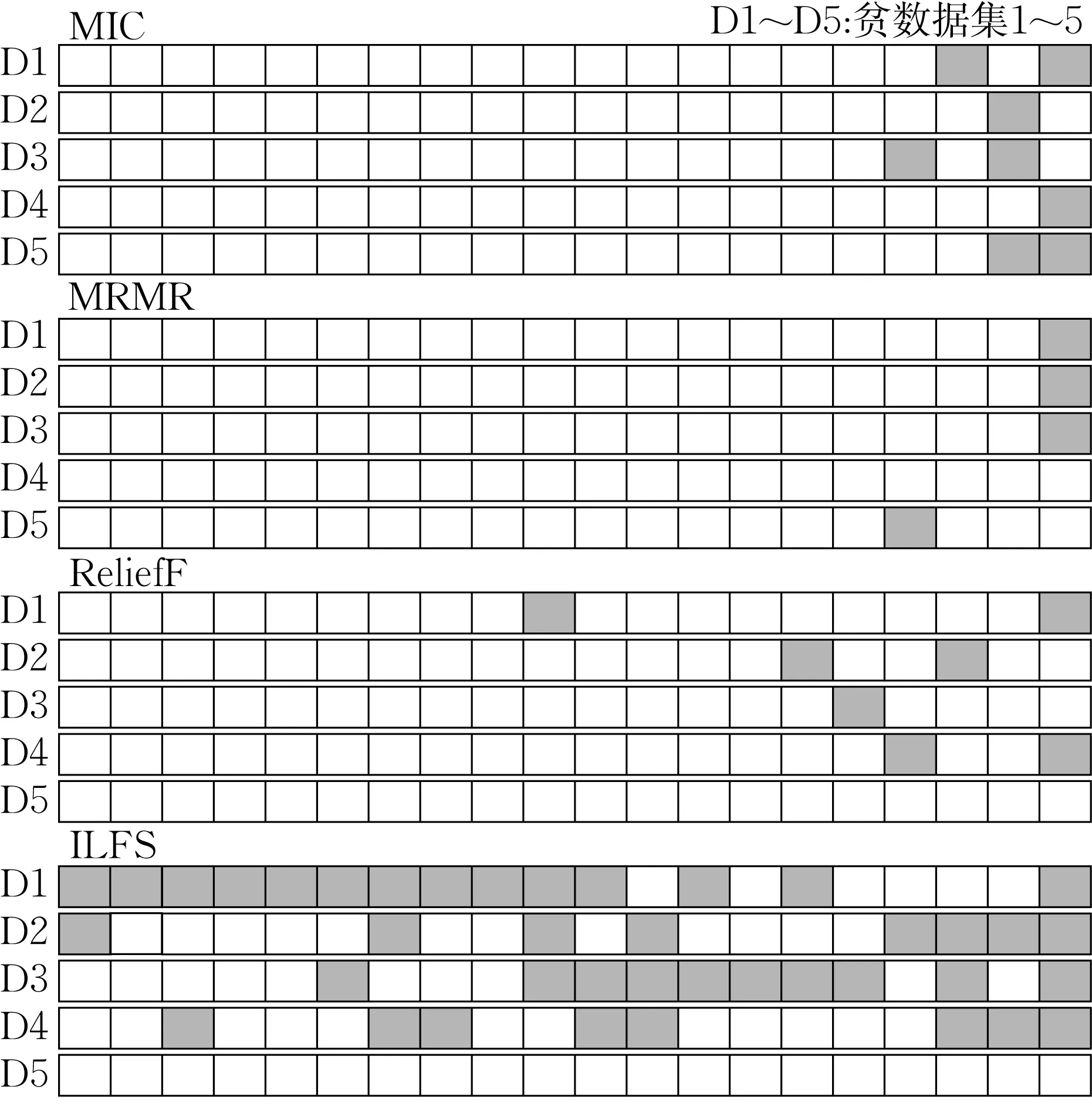
图3 4种特征选择算法在贫数据情景下的稳定性可视化Fig. 3 Robustness visualization of feature selection algorithms in poor data scenario

2.3 DBN自训练模型诊断结果及分析

自训练算法在缺少故障信息时能大幅提升模型的诊断准确率，很适合于贫数据情景，但是其提升效果会受到初始贫数据样本数量的影响，也受到自训练迭代过程中伪标签抽样策略的影响。

现将样本总量13 281 个按7：3随机划分为训练集和测试集，将训练集划分为故障标签和无故障标签的样本集。在上文特征选择工作中，DBN 利用655个训练样本及其最优特征子集即可达到90%以上的诊断准确率，说明此时训练数据相对充分。鉴于上述结果，为模拟实际工程中标签样本匮乏的贫数据情景，在训练集中分别取2.5%、5%及10%的样本组成3 种大小不同、均含有准确故障标签信息的初始训练集，分别代表 “故障样本匮乏” 、 “故障样本稀少” 、 “故障样本充足” 3类情景。同时选取一定量的无标记样本子集。所有数据子集均分层抽样，以保证各工况样本数量均匀分布。在自训练的每一代模型预测结果中，都选取置信度高的故障预测作为无标记样本的伪标签。设定如图4 所示 的 “均匀抽样” 及 “按比例抽样” 2种策略， “均匀抽样” 为每种工况选取相同数量的伪标签，使训练集始终保持平衡； “按比例抽样” 是对每类预测按相同比例抽取伪标签。

图4 均匀抽样策略及按比例抽样策略Fig. 4 Uniform sampling and proportional sampling

2.3.1 贫数据样本量对DBN自训练效果的影响

取故障标签数量比例分别为2.5%、5%和10%的3种贫数据样本同时作为自训练DBN的初始训练集和单纯DBN 的训练集，取MRMR 的特征子集维度N为20，以其作为各模型每次训练的输入特征，保持无标签样本集均一致。当自训练满足退出条件时停止，本文设置的退出条件包含两条：①当伪标签数量不能满足伪标签筛选策略（均匀抽样和按比例抽样）的采样数时自训练停止；或者②当无标签训练集为空时自训练停止。后者是为了防止自训练陷入死循环，实际自训练停止通常由条件①触发。模型评估采用诊断准确率表征模型诊断性能。图5给出在不同比例贫数据样本量下将DBN 模型嵌入自训练算法前后、即单纯DBN 和DBN 自训练的诊断准确率，其中DBN 自训练的诊断准确率均按照 “均匀抽样” 及 “按比例抽样” 2 种策略取平均值；各诊断准确率均为多次平均。

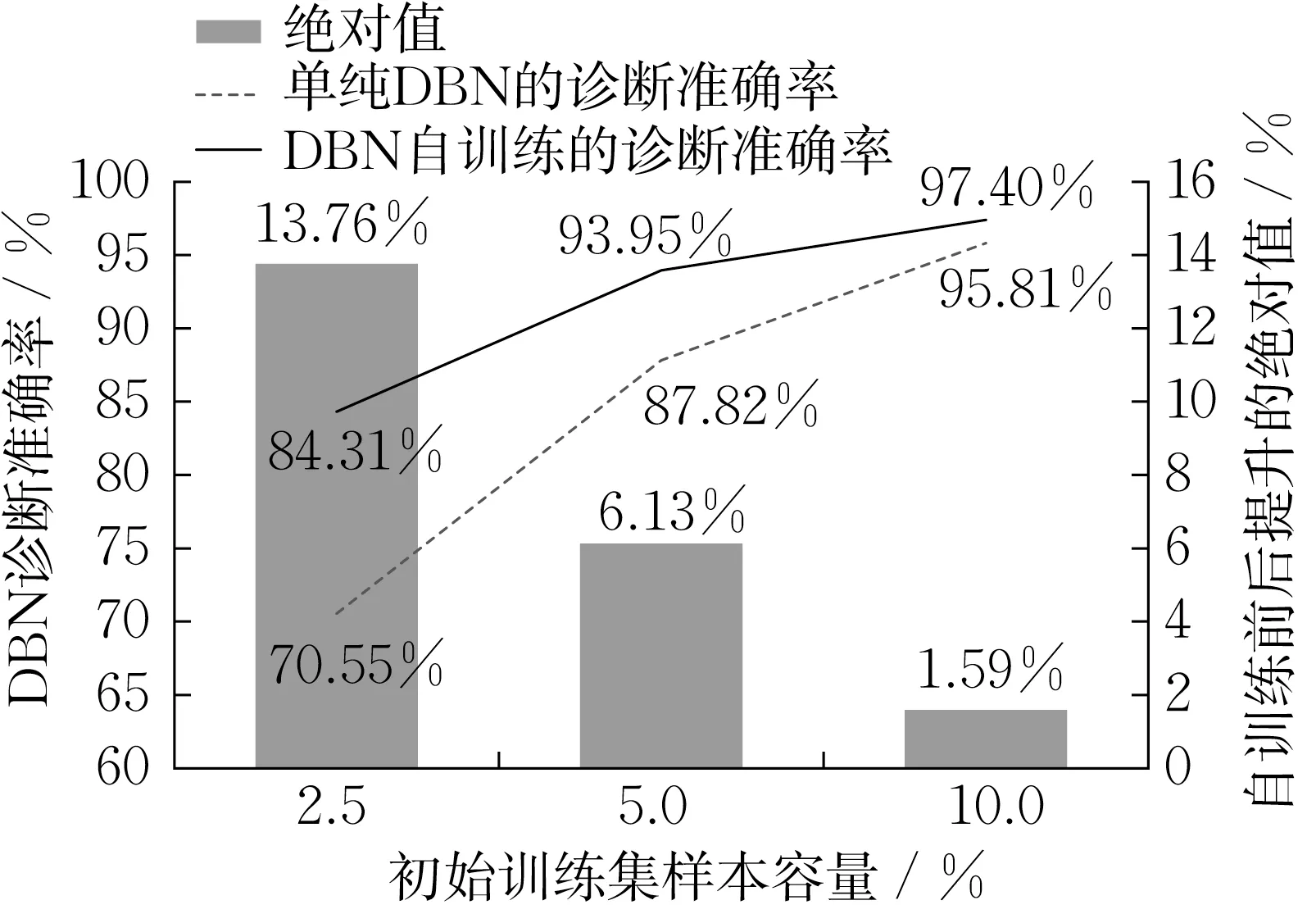
图5 不同贫数据样本量对DBN自训练诊断准确率影响Fig. 5 Influence of different sample sizes of poor data on the accuracy of DBN self-training model

由图5可见，随着贫数据样本数量比例的增大，DBN 自训练模型及单纯DBN 模型的诊断准确率都会提高，但是前者准确率始终高于后者，当初始训练集包含2.5%的故障标签、即贫数据故障样本匮乏时，嵌入自训练算法对模型诊断性能的提升最显著，DBN 自训练的诊断准确率较单纯DBN 从70.55%提高至84.31%，绝对值提高13.76%，相对百分比提高19.5%；而当初始训练集包含10%的故障样本、即故障样本充足时，自训练算法对模型的性能提升相对降低，诊断准确率仅提高1.59%，相对百分比仅提升1.66%。由此可见，在故障标签匮乏时，本文所提出的基于DBN 自训练的故障诊断方法能够利用无标记数据有效提升诊断性能，自训练模型准确率提升的效果与故障标签数量有关，当故障样本稀少、输入DBN 模型的故障信息有限时，自训练模型可生成无标记样本的伪标签，可将更多有效信息输入模型，使诊断性能大幅提升；但若故障标签充足时，输入DBN 模型的故障信息本来已较全面，则自训练模型提升准确率的效果降低。

2.3.2 伪标签抽样策略对DBN自训练的影响

（1） 均匀抽样策略

保持各工况样本数量平衡，初始训练集仍采用前述故障标签数量比例分别为2.5%、5%和10%的3组贫数据样本。在DBN自训练中采用均匀抽样策略不断扩充训练集。对于每类工况均设置抽样数分别为5、10、20、30 的4 种情景，相应的伪标签数量分别为95、190、380、570。图6给出在实施均匀抽样策略时4种情景的DBN自训练诊断准确率。

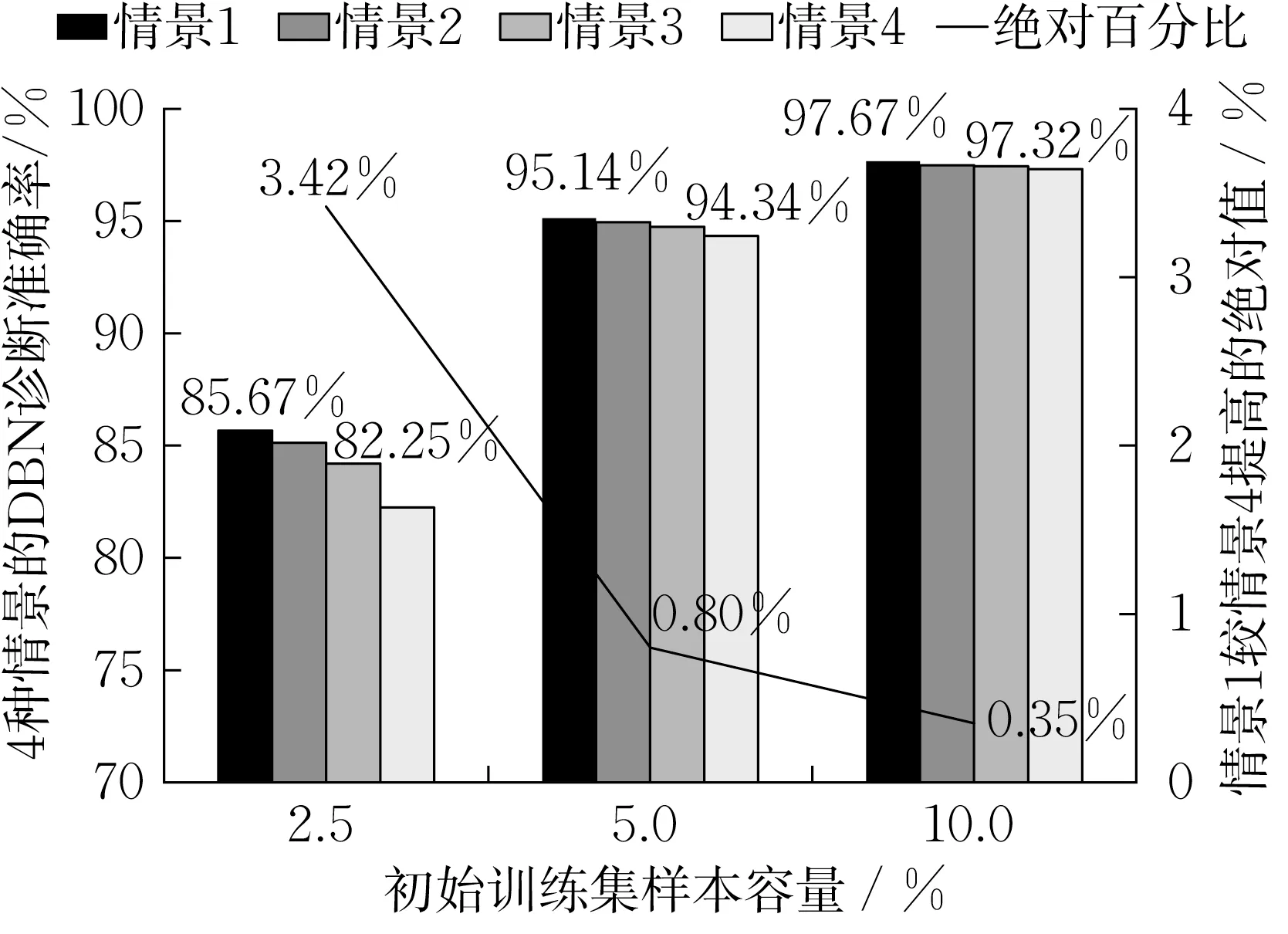
图6 均匀采样策略4种情景的DBN自训练诊断准确率Fig. 6 Accuracy of DBN self-training for four scenarios in uniform sampling.

由图可见，观察每一种不同的贫数据样本量实验，都会发现情景1、即抽样数为5的DBN自训练诊断准确率始终最高，且随着抽样数的增加而降低。比如在初始训练集包含2.5%故障标签的贫数据样本量实验中，情景1 即抽样数为5 的DBN 自训练诊断准确率为85.67%，在4种情景中最高，它比情景4即抽样数为30 的准确率82.25%高出3.42%，这主要是由于当嵌入自训练算法后，采用均匀抽样策略，若抽样数越小，选择要求越严格，则伪标签整体置信度较高，因此DBN 自训练的诊断准确率也较高；反之，抽样数越大，采样到误分类的伪标签（即噪声）的概率越大，故模型自训练诊断准确率降低。当然，值得注意的是，过低的抽样数会导致自训练过程迭代次数增多，增加自训练计算量。

此外，若对比初始训练集包含不同比例故障标签的贫数据样本量实验，发现由抽样数造成的诊断准确率差异随着贫数据样本量的增加而减小，比如在2.5%贫数据的故障样本匮乏时，4种情景之间的最大诊断准确率，即情景1抽样数5比情景4抽样数30高出3.42%；在5%贫数据的故障样本稀少时，这一提升比例降至0.8%；而在10%贫数据的故障样本充足时，这种优势缩小到仅为0.35%。这是因为，随着故障标签贫数据样本量的增大，单纯DBN模型的诊断准确率也相对提高，伪标签误分类情况改善，置信度高的样本伪标签误分类数量减少，抽样数增加给训练集带来的噪声较少。因此这时，较小抽样数的诊断准确率并未提高多少，但其FDD计算量却很大。所以抽样数的选取，需要同时兼顾贫数据样本量和训练时间。

（2） 均匀抽样策略与按比例抽样策略的影响对比

伪标签抽样策略对自训练算法的诊断准确率影响很大。但当前相关研究中，往往是简单地根据所有种类伪标签置信度统一降序排列并按比例抽样，而这样可能会出现严重的类间不平衡、引入过多噪声并降低诊断准确率。本文前面已采用均匀抽样策略，现尝试采用按比例抽样，先在类内根据置信度对样本进行降序排列，再取类内故障预测标签总数一定比例的伪标签扩充训练集，并将均匀抽样及按比例抽样2种策略对DBN自训练的诊断准确率影响进行对比。实验中3 组贫数据样本量同前，设置按比例抽样伪标签总数分别为190和380这2种情景，图7 给出在不同贫数据样本量中每种抽样策略下2 种情景的DBN自训练诊断准确率。由图可见，按比例抽样策略对诊断准确率的影响与均匀抽样类似，准确率也是随着抽样比例的增大而降低，说明抽样比例的扩大同样会给训练集带来更多噪声。

图7 2种抽样策略2种情景的DBN自训练诊断准确率Fig. 7 Accuracy of DBN self-training for two scenarios in two sampling strategies.

将2 种抽样策略进行对比，在故障标签数量比例分别为2.5%、5%和10%的3 组贫数据样本中，每种情景下都使2 种抽样策略保持相同的抽样总数，由图7看出，均匀抽样的诊断准确率普遍高于按比例抽样。在初始训练集只包含2.5%的贫数据故障样本匮乏时，在情景1 即抽样总数为190 时，均匀抽样及按比按抽样的DBN 自训练诊断准确率分别为85.12%和83.73%，前者比后者高1.39%；在情景2 即抽样总数为380 时，二者的准确率分别为84.20%和83.40%，前者比后者高0.80%。当贫数据样本量增加到5%达到稀少时，均匀抽样较按比例抽样的优势缩小到0.75%～1.12%，而贫数据样本量到10%即故障样本充足时，优势进一步缩小到0～0.47%。由此可见，均匀抽样策略较优，但其优势将随贫数据样本量的增大而降低。造成按比例抽样劣势的原因在于，前几代DBN自训练模型在贫数据情景下诊断性能不佳，在给无标记样本预测故障时，易出现误分类情况，因此导致每种工况按照比例选取的伪标签存在不平衡现象。

为更清晰地对比2种抽样策略对DBN自训练诊断性能的影响，图8 给出初代DBN 诊断模型对伪标签的预测效果。如图8中的工况5，当伪标签数量过高时，伴随着低精确率和高召回率，这是由将其他故障样本误分类为本类样本（FP）所致，而按比例抽取伪标签，不仅会加剧这种类间不平衡，而且将更多噪声（误分类标签）引入训练集，因此会降低诊断准确率。而与之相反，如图8 中的工况4，其较低的伪标签数量通常伴随较高的精确率，均匀抽样相对于按比例抽样，减少了精确率低的样本采样，引入噪声概率小，故有利于提高自训练的诊断准确率。

图8 初代DBN模型的故障预测分布Fig. 8 Fault prediction distribution of the first generation for DBN model

3 进一步讨论

3.1 图2与图5描述问题的差异

对比图2和图5的主纵坐标可见，虽然二者皆为DBN FDD的诊断准确率，但它们有本质不同。图2描述的是单纯DBN 模型的故障诊断性能随着样本特征数量增加而提升的特点，而图5 描述的是DBN自训练模型与单纯DBN模型相比较、前者诊断性能的优势随着初始训练样本量的增大而降低的特点。图2与图5描述的是不同的实验现象，从数据维度解释，若将实验数据视为二维张量，图2 和图5 分析的是不同维度下的实验现象，图9 或能直观展示出二者的差异。

图9 图2与图5在数据维度方面的差异Fig. 9 Fig. 2 VS Fig. 5 from the aspect of data dimension

3.2 对DBN自训练中可能出现的随机抽样策略的讨论

文中所研究的 “均匀抽样” 和 “按比例抽样” 2 种情景，均为目前研究文献中比较模棱两可、但却在基于数据驱动FDD中比较典型的抽样情景，对其进行研究具有一定的理论意义和实际应用价值。

在DBN自训练中，随机抽样也是实际情况中或许会出现的一种情景，但是，由于无任何条件限定的随机抽样极易导致自训练模型性能恶化，因此这种随机抽样情景并没有太多实际意义；而满足一定边界条件限定下的随机抽样更有研究价值。

例如：可以研究在 “对伪标签置信度阈值进行设置” 条件下的随机抽样，通过对最佳阈值设定方法、特点及规律的探究，更好地在伪标签质量及自训练迭代效率间取得平衡，以不断提升被扩充数据的总体质量，更好地挖掘自训练算法的价值，提升模型诊断精度。

或者研究在 “对类间抽样或类内抽样进行设定” 条件下的随机抽样，这时，由于类间随机抽样是将所有故障工况的伪标签合并抽样，由此可能产生数据不平衡情景中的FDD问题，由于其极易致使模型诊断性能退化，也是目前FDD 研究中的难点；而类内随机抽样，则可以归并入文中研究的2种策略。

以上工作还有待于进一步探究。

4 结论

本文模拟实际工程中AHU故障数据匮乏情景，基于深层网络DBN模型对4种特征选择算法的最优特征子集特性进行对比研究；为提升贫数据时的分类器诊断性能，提出将DBN 模型嵌入自训练框架的故障诊断模型，分别探讨初始数据集容量大小及不同伪标签抽取策略对自训练性能的影响，主要结论如下：

（1）DBN模型的诊断准确率随特征子集维度的增加而增加，但当子集维度超过20 这个最优值后，诊断准确率的增加趋势逐渐饱和；在所研究的4 种特征选择算法中，MRMR在不同的子集维度下均能保持最佳性能，在贫数据时的诊断性能及子集元素稳定性最优，说明其对冗余特征剔除的策略有效。

（2）深层网络自训练算法能够有效提升故障信息匮乏情景下模型的诊断性能。当初始训练集包含2.5%的故障标签、即贫数据样本量很低时， DBN自训练较单纯DBN的诊断准确率可以提高19.5%；随着贫数据样本量的增加，其准确率提升幅度渐小，说明本文提出的DBN 自训练算法适用于故障信息匮乏的情景。

（3）伪标签抽样策略对故障标签匮乏时DBN自训练模型的诊断性能影响很大。均匀抽样及按比例抽样2种策略对DBN自训练诊断准确率的影响情况类似，二者在抽样数较小时均表现出更优的性能，在不同抽样数下的诊断准确率最大相差3.42%；在不同贫数据样本量中，均匀抽样始终优于按比例抽样，诊断准确率最大相差1.39%。因此，在故障标签匮乏、初始诊断模型性能不佳时，均匀抽样策略更为适用。

作者贡献声明：

孟华：参与研究的构思、设计，对主要学术性内容做文稿修订；

裴迪：进行研究的构思、设计，数据运算，起草论文；

阮应君：对重要学术性内容提出建议，做出修订；

钱凡悦：参与研究的构思、设计；

邓永康：参与研究的构思、设计；

郑铭桦：参与研究的构思、设计。