风光储直流微电网的双输入MPPT控制策略分析

金叶 邢凯淞 张哲 张岩

摘 要：针对以输出功率为判断标准的传统的单输入扰动观察法（下文简称为“传统扰动观察法”）存在的弊端，提出一种可用于风光储直流微电网的双输入变步长扰动观察法（下文简称为“双输入MPPT控制策略”），并对风电机组和光伏发电系统分别采用两种控制策略时的占空比、发电效率等进行了对比分析。分析结果显示：相较于传统扰动观察法，风电机组采用双输入MPPT控制策略追踪最大功率点后，扰动步长减小90%的同时追踪时间减少了72.3%；光伏发电系统采用双输入MPPT控制策略追踪最大功率点后，扰动步长减小90%的同时追踪时间减少了39%。仿真结果验证了双输入MPPT控制策略的有效性，该策略适用于电感参与调压的多种场景。

关键词：光伏发电；风电；蓄电池；风电机组；微电网；最大功率点跟踪；扰动观察法

中图分类号：TM615/TM614 文献标志码：A

0  引言

中国已建成很多大型的风电场及光伏电站，通过采用集中式控制策略保证其整体的输出功率可控，且此种控制策略已较为成熟，应用也很广泛[1]。然而对于一些小型风电机组和小型光伏发电系统而言，更多的是需要采用针对小型设备的控制策略，因为这些系统只有成本较低才具有应用价值[2]。而采用风电、光伏发电和蓄电池综合输出的新能源发电系统（即“风光储直流微电网”）常用的控制策略为最大功率点跟踪（MPPT）策略。

文献[3]建立了光伏组件仿真模型及MPPT模型用于分析温度和光照强度对光伏组件输出特性的影响，并将Boost升压斩波电路用于光伏组件硬件电路，但此方式未能保证光伏组件输出电压恒定。文献[4]介绍了光伏发电系统常用的光伏MPPT方法，例如：恒定电压法、扰动观察法、电导增量法等，并提出了基于模糊控制器的MPPT方法，但该方法使用时模糊控制器的模糊参数需要根据实际情况调试，在不同条件下参数差异较大，不易在工程实践中推广。文献[5]介绍了小型风电机组常用的硬件电路方案，但由于负载的阻值恒定，导致该电路仅能跟踪稳定功率而无法跟踪最大功率点。文献[6]介绍了风电机组常用的MPPT方法，例如：爬山搜索法、最佳叶尖速比法等，并提出了基于模糊比例-积分-微分（PID）控制算法的MPPT方法，但该方法同样存在模糊参数需调试的问题。文献[7]介绍了常用的双向DC-DC变换器的硬件结构，但未对该变换器的电路结构进行深入分析。文献[8]介绍了混合储能系统的控制策略，通过电压外环控制、电流内环控制的双闭环比例-积分（PI）控制策略维持了直流母线电压的稳定，但未涉及风电机组转速稳定性及MPPT策略。

考虑到上述文献的不足，本文在改进以输出功率为判断标准的传统单输入扰动观察法（下文简称为“传统扰动观察法”）的基础上，提出一种可用于风光储直流微电网的双输入变步长扰动观察法（下文简称为“双输入MPPT控制策略”），即该策略通过控制直流母线电压维持在恒定值来调整风电机组和光伏发电系统的输出电压，并进行对比验证。

1  基于双输入MPPT控制策略的风光储直流微电网介绍

本文利用Matlab/Simulink软件建立了基于双输入MPPT控制策略的风光储直流微电网仿真模型，其中，储能系统采用蓄电池。该控制策略通过调整直流母线电压可控制储能系统在充电模式和放电模式之间切换，从而形成直流微电网。基于双输入MPPT控制策略的风光储直流微电网结构图如图1所示。图中：C1为电容；U1为电压采集模块；u为模块内通过的电压；Udc为直流母线电压。采用与电容并联的电阻来模拟用电负荷，通过电压采集模块对直流母线电压进行实时监测，观察各子系统的工作情况。

本微电网采用永磁直驱型风电机组，通过不控整流电路将风电机组发出的交流电转换为直流电，再通过Boost升压斩波电路将直流电压转换成标准电压为储能系统充电。该风电机组采用双输入MPPT控制策略，可维持功率系数为最大值。光伏发电系统同样采用双输入MPPT控制策略，可使其输出电压和输出电流保持在最大功率点下的理论最佳输出电压和理论最佳输出电流。根据Matlab/Simulink 软件的多次仿真结果显示，该微电网中风电机组的发电效率达到98%以上，光伏发电系统的发电效率达到99%以上才符合设计要求；双输入MPPT控制策略可使本微电网具有更快的追踪速度、更好的控制精度及更高的发电效率。本微电网的工作流程图如图2所示。图中：?d为扰动步长；v为风速；?Pm、?P分

别为风电机组和光伏发电系统的输出功率变化量；P为输出功率；?U为输出电压变化量；U为输出电压；Cp为风能利用系数，代表风电机组能够从风能中吸收的能量比例，风能利用系数是一个有關叶尖速比和桨距角的非线性函数，根据贝茨极限理论，其理论最大值为0.593；?Cp为风能利用系数变化量；λ为叶尖速比；?λ为叶尖速比变化量；D为占空比；U*为目标电压值。

2  各子系统的控制策略分析

2.1 储能系统充放电控制

储能系统需具有提供电能和储存电能的功能，也意味着其必须具备电能双向变换的能力，因此本微电网的储能系统采用双向DC-DC变换装置。本储能系统的主电路仿真图如图3所示。图中：S1、S2分别为IGBT1和IGBT2的控制开关；g、E、C分别为栅极、发射极、集电极；VM为电压测量模块；IL6为电流测量模块；i为模块内通过的电流；Isc为蓄电池的电流；L为电感；Usc为蓄电池的电压。

图3所示主电路为双向半桥DC-DC变换电路，其桥臂上有两个同向的IGBT模块且这两个IGBT模块的控制开关状态互补（即不能同时导通或关断）。电压测量模块负责监测蓄电池电压，电流测量模块负责监测蓄电池电流。

本储能系统的主电路存在两种工作模式：

1） Boost升压斩波模式。此模式下若S1导通、S2关断，则蓄电池将能量转移到电感上；若S1关断、S2导通，则蓄电池和电感共同向直流母线充电，可保持直流母线电压稳定。

2）Buck降压斩波模式。此模式下若S1关断、S2导通，直流母线向电感和蓄电池同时充电；若S1导通、S2关断，电感将存储的能量转移至蓄电池。

对储能系统仿真时采用Matlab/Simulink软件自带的蓄电池模块，设置直流母线电压为400 V，由电压外环电流内环的双闭环PI控制策略决定主电路IGBT模块的占空比。仿真结果显示，双闭环PI控制策略可使直流母线电压稳定在400 V不变，具体如图4所示。

根据电感电流的流动方向可以确定主电路的工作模式：

1）当接入负载时，直流母线电压降低，需要蓄电池提供能量维持直流母线电压稳定，电感电流由蓄电池流向直流母线，此时主电路工作在Boost升压斩波模式。风电机组、光伏发电系统与蓄电池的总输出功率与負载消耗的总功率相当。当接入负载时蓄电池的输出功率曲线、荷电状态（SOC）曲线分别如图5、图6所示。

2）当不接入负载或负载功率较低时，可将蓄电池看作负载，直流母线电压较高，需向蓄电池输出能量保持电压稳定，电感电流由直流母线流向蓄电池电路，此时主电路工作在Buck降压斩波模式。风电机组、光伏发电系统的输出功率与蓄电池接收的功率相等。当不接入负载时蓄电池的输出功率曲线、SOC曲线分别如图7、图8所示。

2.2  风电机组MPPT控制策略

对于永磁直驱型风电机组，其输出功率Pm、

风轮吸收的风能支撑风电机组叶片旋转，稳态时风轮输出功率和风电机组输出功率数值相等，即风电机组输出功率可表示：

式中：ρ为空气密度；R为风轮半径。

建立风电机组的主电路仿真模型，如图9所示。图中：A、B、C分别代表A相线、B相线、C相线；p为风电机组的输入功率；K为目标输出功率的系数；Cw为风电机组的发电效率；m为风电机组内部测量信息的输出端。

图9中的风电机组整流及升压模块采用三相不控整流电路和Boost升压斩波电路，占空比由风电机组MPPT模块控制。该方法是对占空比施加一定步长的扰动，当占空比增大时观察风电机组输出功率是否增大，若增大，则继续增大占空比；反之，则减小占空比。

当占空比设置为0.5和0.6时，可测得在两种风速下风电机组的输出参数，具体如表1所示。

由表1可知：增加占空比能降低风电机组输出的整流电压，进而降低风电机组的角速度；角速度降低会使叶尖速比向最佳叶尖速比靠近，进而增大风能利用系数，风电机组输出功率也随之增大，并向最大输出功率移动。

不同桨距角时风电机组的风能利用系数曲线如图10所示。图中：β为桨距角；Cp，max为风能利用系数最高值。

由图10可知：在桨距角为零的情况下，当叶尖速比降低至8.1时，风能利用系数可达到最高值0.48。

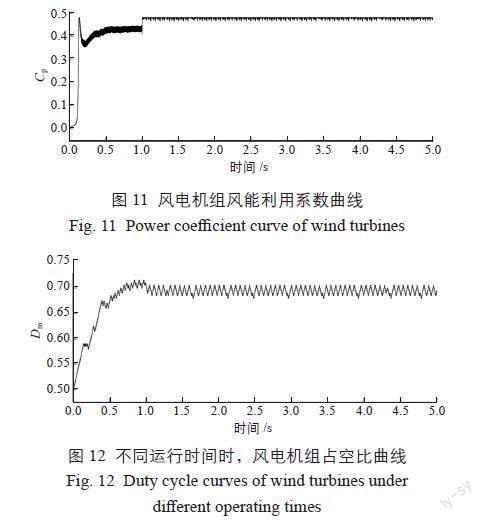
设置占空比为0.5、扰动步长为0.005时，运行风电机组MPPT模块后，观测到风电机组输出功率持续上升至理论最大值1940 W；风能利用系数持续升高至0.48，具体如图11所示；此时风电机组转矩升高至178 N·m、角速度降低至10.9 rad/s。不同运行时间时，风电机组占空比Dm曲线如图12所示。由图12可知：在较短时间内，风电机组占空比就达到了相对稳定。当风电机组占空比稳定在0.7左右时，风电机组发电效率可达98%以上。

综上可知，大扰动步长的设置可以提高风电机组发电效率，加快最大功率点的追踪速度。但是传统扰动观察法存在缺陷，其无法兼顾减小振幅和提高追踪速度这两个目标。通过分析风电机组的硬件电路可以发现，Boost升压斩波电路存在电感，使风电机组输出电流产生与电力电子开关同频率的震荡，这种震荡也会影响风电机组输出功率曲线，使其出现波动。由于传统扰动观察法只有输出功率这一个输入参数，无法正确区分输出功率的传递方向。在扰动步长较小的情况下，当出现通过调整占空比造成的输出功率变化小于或等于输出电流波动引起的输出功率变化的情况时，则说明传统扰动观察法是失效的，因此必须增大扰动步长。该传统扰动观察法中占空比的扰动步长调整为0.005时最大功率点追踪效果较好，但造成占空比具有较大波动，影响风电机组发电效率继续提升。较大的扰动步长也会造成风电机组转速、转矩、输出的整流电压都有较大波动。

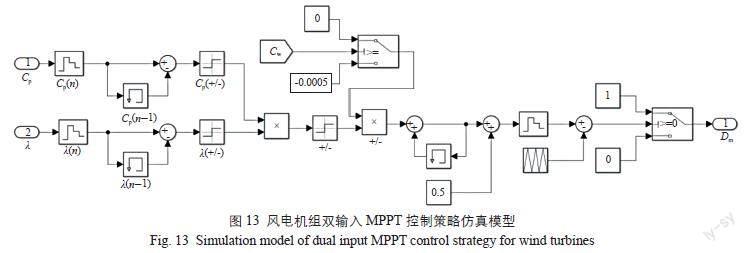
为避免风电机组输出电流波动对追踪速度造成的影响，参考风电机组极值搜索法[9]和变步长控制策略，设计了双输入MPPT控制策略，以替代传统扰动观察法。风电机组双输入MPPT控制策略仿真模型如图13所示。图中：n为当前采样时刻。

结合式（1）、式（2）、图10可知：当桨距角为零时，风电机组的每1个叶尖速比都有1个风能利用系数与其相对应，且两者之间为非线性关系[10]。

根据电磁感应定律：

式中：Um为风电机组的输出电压；B为磁感应强度；l为导线长度。

根据式（2），可将检测得到的风电机组输出功率与固定倍数的风速三次方的比值作为风能利用系数；结合式（1）～式（3）可知，风电机组输出电压与风电机组角速度线性相关。因此可将风电机组输出电压与固定倍数的风速的比值作为叶尖速比。这就避免了对小型风电机组进行复杂的有关风能利用系数的函数拟合。对于风能利用系数变化量和叶尖速比的变化量而言，若二者都为正，代表扰动为负且方向正确，应继续增大风电机组的输出电压，减小占空比；若二者都为负，代表扰动为正但方向错误，应增大风电机组的输出电压，减小占空比。二者为一正一负时，若风能利用系数变化量为正、叶尖速比的变化量为负，代表扰动为正且方向正确；若风能利用系数变化量为负、叶尖速比的变化量为正，代表扰动为负且方向错误，这两种情况都应减小风电机组的输出电压，增大占空比。

在风电机组发电效率低于98%时采用双输入MPPT控制策略，在风电机组发电效率高于98%后切换至固定占空比状态，这样可使风电机组在快速跟踪到最佳占空比后保持占空比恒定，提高其工作效率。

2.3  光伏发电系统MPPT控制策略

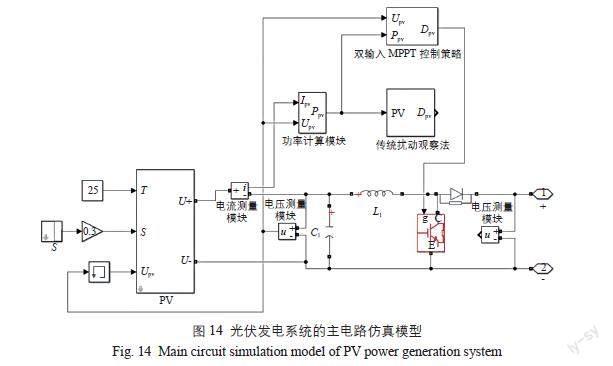
本光伏发电系统采用Boost升压斩波电路升高光伏阵列输出电压，占空比是由输出功率经扰动观察模块比较后输出。光伏发电系统的主电路仿真模型如图14所示。图中：PV为光伏阵列模块；T为环境温度；S为太阳辐照度；Upv为光伏阵列输出电压；Ppv为光伏阵列输出功率；Ipv为光伏阵列输出电流；Dpv为光伏阵列占空比。

光伏发电系统以环境温度、太阳辐照度及光伏阵列输出电压作为输入参数，经电压测量模块和电流测量模块测量后将数值传至控制系统。

将占空比保持在0.5，可观测到光伏阵列输出电压保持在200 V，输出电流较大，输出功率无法追踪最大功率点，发电效率偏低。固定占空比时光伏阵列的输出功率曲线如图15所示。图中：红线是经计算得出的光伏阵列理论最大输出功率曲线；蓝线是在固定占空比情况下得到的光伏阵列输出功率曲线。

设置占空比为0.5，扰动步长为0.01，则光伏阵列输出电压和输出电流跟随最大功率点电压和最大功率点电流，此时，输出功率始終跟踪最大功率点。采用传统扰动观察法时光伏阵列的输出功率曲线如图16所示。图中：红线是经计算得出的光伏阵列理论最大输出功率曲线；蓝线是在固定占空比情况下得到的光伏阵列输出功率曲线。

由图17可知：尽管传统扰动观察法下得到的光伏阵列占空比曲线可以追踪并保持在最佳占空比（0.4）附近，但无法兼顾追踪速度与精度，而提高追踪速度必然要付出精度降低导致占空比剧烈波动的代价。

光伏发电系统的输出电流波动会造成其输出功率的波动，为避免输出电流波动对追踪速度的影响，参考电导增量法[4]和变步长控制策略设计了双输入MPPT控制策略替代传统扰动观察法。该控制策略的工作原理可概括为：

1）检测光伏发电系统的输出功率变化量和输出电压变化量，若二者都为正，代表扰动为负且方向正确，应继续增大光伏发电系统的输出电压，减小占空比。若二者都为负，代表扰动为正且方向错误，应增大光伏发电系统的输出电压，减小占空比。当二者为一正一负时，若输出功率变化量为正、输出电压变化量为负，则代表扰动为正且方向正确；若输出功率变化量为负、输出电压变化量正，则代表扰动为负且方向错误，两种情况都应减小光伏发电系统的输出电压，增大占空比。

2） 光伏发电系统将在输出效率达到99%后切换至固定占空比状态。

光伏发电系统双输入MPPT控制策略仿真模型如图18所示。图中：Cpv为光伏发电系统的发电效率。

3  双输入MPPT控制策略效果及结果分析

利用Matlab/Simulink软件对采用双输入MPPT控制策略的风光储直流微电网各子系统进行仿真，仿真参数如表2所示，仿真结果如表3所示。

分析表3数据可以发现：风电机组和光伏发电系统的实际输出电压比理论值高，这是因为双输入MPPT控制策略采用的是先升压再降压的功率追踪方法，能更快追踪到最大功率点。光伏发电系统在电感的帮助下甚至能有比理论最大值更大的瞬时输出功率。

双输入MPPT控制策略下的风电机组占空比曲线、风电机组扰动方向、风电机组发电效率曲线及传统扰动观察法下的风电机组发电效率曲线分别如图19～图22所示。

结合图10、图19～图22可知：在桨距角为零的情况下，叶尖速比达到最大值之前，风能利用系数逐渐升高，此时占空比先下降；风能利用系数到达最高点0.48后，随着叶尖速比升高，风能利用系数开始降低，占空比逐渐升高。在叶尖速比达到最大值后，持续升高的占空比使叶尖速比开始下降，风能利用系数升高，直至风电机组发电效率达到98%以上，此时，风电机组切换扰动步长，运行在固定占空比状态，使风电机组维持在最高输出功率直至风速发生变化。

双输入MPPT控制策略下的光伏发电系统占空比曲线、光伏发电系统输出电压曲线、光伏发电系统发电效率曲线及传统扰动观察法下的光伏发电系统发电效率曲线分别如图23～图26所示。

结合图23～图26可知：在光伏发电系统输出电压升高至开路电压之前，占空比短暂降低，接近开路电压时，输出电流为零，输出功率为零，此时占空比开始升高，升高期间随着输出电压降低和输出功率的升高，占空比持续升高；由于输出电流较小，其波动对输出功率的影响未能使输出功率降低，因此剔除了输出电流波动的影响。光伏发电系统可以在较小扰动步长下以很短的时间达到目标占空比，到达目标占空比后切换扰动步长至固定占空比状态。

双输入MPPT控制策略避免了Boost升压斩波电路的固有缺陷，达到了剔除电感电流脉动对扰动方向检测的干扰，对比传统扰动观察法，双输入MPPT控制策略反应迅速，无杂波干扰，且到达目标占空比后迅速稳定，因此可以做到追踪精度和追踪速度的同时控制，具有工程实用价值。

综上可知，相较于传统的扰动观察法，采用双输入MPPT控制策略后，风光储直流微电网各子系统的占空比曲线更平滑，追踪时间更短且追踪至目标占空比后能保持在目标值恒定，这使各系统的输出功率更高，更具有优越性。仿真结果显示，相较于传统扰动观察法，风电机组采用双输入MPPT控制策略追踪最大功率点后，扰动步长减小90%的同时追踪时间减少了72.3%；光伏发电系统采用双输入MPPT控制策略追踪最大功率点后，扰动步长减小90%的同时追踪时间减少了39%。

4  结论

本文针对传统扰动观察法存在的弊端，提出了一种可用于风光储直流微电网的双输入MPPT控制策略，并对风电机组和光伏发电系统分别采用两种控制策略时的占空比、发电效率等进行了对比分析。分析结果显示：相较于传统扰动观察法，风电机组采用双输入MPPT控制策略追踪最大功率点后，扰动步长减小90%的同时追踪时间减少了72.3%；光伏发电系统采用双输入MPPT控制策略追踪最大功率点后，扰动步长减小90%的同时追踪时间减少了39%。通过采用先升压再降压的方案，能够很好避免Boost升压斩波电路中电流波动引起的不良影响，能顺利过滤杂波，快速准确追踪最大功率点。

在实际工程应用中，可利用双输入MPPT控制策略的快速追踪能力和高追踪精度特性对风光储直流微电网进行数据拟合，反推其功率系数函数。在直流微网电压稳定的情况下，通过调整占空比可令接入的光伏发电系统和风电机组均处于MPPT模式。本文所提出的双输入MPPT控制策略适用于电感参与调压的多种场景。

[参考文献]

[1] 王宗瑞，李昔真，苏则立. 中国风光互补联合发电技术的现状与展望[J]. 节能，2017，36（8）：4-7，2.

[2] 钱苏翔，詹彦，熊远生. 扰动观察法在小型风机MPPT中的仿真研究[J]. 机械设计与制造，2013（8）：165-168.

[3] 张智龙. 微电网运行仿真技术及控制策略研究[D]. 沈阳： 东北大学，2014.

[4] 赵川. 光伏发电系统最大功率跟踪控制系统研究[D]. 西安：长安大学，2018.

[5] 王鹏. 小型独立式风光互补发电系统的研究与设计[D]. 青岛：山东科技大学，2020.

[6] 邵泽锋. 基于MPPT算法小型风光互补发电系统集成控制的研究[D]. 抚顺：辽宁石油化工大学，2019.

[7] 沙梦琪，王勇. 基于母线电压的储能直流变换器下垂控制策略[J]. 电力电子技术，2023，57（2）：56-59.

[8] 敦若楠，郭英军，孙鹤旭，等. 基于混合储能的直流微网母线电压控制策略[J]. 河北工业科技，2019，36（6）： 384-389.

[9] 程启明，程尹曼，汪明媚，等. 风力发电系统中最大功率点跟踪方法的综述[J]. 华东电力，2010，38（9）： 1393-1399.

[10] 金叶，张岩，金雨晴，等. 双馈风力发电机功率控制方式的改进方案及验证[J]. 电气应用，2023，42（2）：92-101.