考虑风光不确定和阶梯式需求响应的园区综合能源系统博弈优化运行

徐光晨,薛田良,张 磊,赵雅洁

(三峡大学电气与新能源学院,湖北 宜昌 443002)

0 引言

随着“双碳”目标的提出,缓解能源供需矛盾,完成能源高效利用,实现系统经济低碳运行已成为迫切需要解决的问题[1-2]。由于园区综合能源系统(park-level integrated energy system,PIES)可以将多种能源进行耦合并对能源完成梯级利用,同时可以兼顾系统运行的安全性和经济性,因此PIES已成为目前能源领域的的研究焦点[3]。

对于PIES优化调度研究,国内外学者已经做了大量研究。文献[4]通过建立多目标优化调度模型来保证PIES运行的经济性和环保性;文献[5]考虑了风光出力的相关性,采用概率模型法对PIES调度运行进行两阶段优化;文献[6]通过引入需求响应策略和多不确定性对PIES内资源进行合理分配。

但是,上述研究并未对PIES中不同主体间的利益竞争进行描述,因此国内外学者受博弈论的启发,着手对多主体PIES调度进行研究。文献[7-8]基于PIES主从博弈优化调度模型综合考虑阶梯型碳交易和阶梯型需求响应,并建立了多主体低碳经济运行交互机制,实现了系统运行的低碳性和经济性,但没有考虑新能源出力的不确定性;文献[9-10]为实现新能源消纳与多能源耦合应用提出了考虑风光不确定和碳交易的PIES博弈优化调度策略,但没有引入用能方柔性负荷概念;文献[11-12]在博弈框架下考虑了用户侧柔性负荷参与需求响应,但其中对于用户的需求响应补贴为常规补贴,用户参与的积极性不高。

因此,为了解决PIES中新能源出力不确定性问题,使调度结果更加贴近实际;同时提高用户参与需求响应的积极性,使得各主体效益得到提高,本文提出了一种考虑风光不确定和阶梯式需求响应的园区综合能源系统博弈优化运行策略。首先,对于源侧风光不确定性问题,采用蒙特卡洛法进行随机场景生成并利用k-means聚类和同步回代法对场景进行缩减;其次,在荷侧考虑用户阶梯式需求响应基础上,以园区运营商和用户聚合商效益最大化为目标,建立PIES主从博弈优化调度模型;最后,同时利用遗传算法和CPLEX求解器在MATLAB中进行仿真验证。算例结果表明所提优化策略可以有效提高园区运营商和用户的效益。

1 PIES框架和设备模型

1.1 PIES框架

本文所研究的PIES框架如图1所示。上级能源商由电网和气网组成;园区运营商由风电机组(wind turbine, WT)、光伏机组(photovoltaic, PV)、燃气轮机(gas turbine, GT)、燃气锅炉(gas boiler, GB)、余热锅炉(waste heat boiler, WHB)、蓄电池(electric storage, ES)、蓄热罐(heat storage, HS)组成;用户聚合商侧的负荷由电负荷、热负荷组成。

图1 园区综合能源系统框架

1.2 燃气轮机建模

燃气轮机是一种能够将气能转化为热能和电能的热电联产设备,其模型如式(1)—式(3)所示。

(1)

(2)

(3)

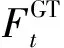
1.3 燃气锅炉建模

燃气锅炉通过燃烧天然气产生热能对余热锅炉不能提供充足热量时进行补偿,其模型如式(4)、式(5)所示。

(4)

(5)

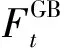
1.4 储能装置建模

园区运营商中储能装置包括ES和HS,其能量储放过程相似,其模型如式(6)。

(6)

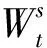
1.5 风光不确定性建模

风力发电机和光伏发电机的出力模型如式(7)、式(8)所示。

(7)

(8)

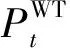
为解决风光的不确定性问题,研究表明风速服从WeiBull分布[13]、光照强度服从Beta分布[14],风光概率模型如式(9)、式(10)所示。

(9)

(10)

式中:cs、ks分别为WeiBull分布的比例参数与形状参数;αs、βs分别为Beta分布的形状参数。

根据WT和PV参数的概率分布,首先利用蒙特卡洛抽样法生成大量场景;然后利用k-means聚类对场景进行缩减得到少量WT和PV典型场景,最后利用同步回代法再次进行场景缩减,得到ω个场景及其对应概率Pω。

2 阶梯式需求响应模型

本文将用户侧负荷分为固定负荷和柔性负荷,固定负荷灵活性较差只能固定接受供能,而柔性负荷具有良好的灵活性,其中柔性包括可转移负荷以及可削减负荷。电、热负荷模型统一如式(11)—式(15)所示。

(11)

(12)

(13)

(14)

(15)

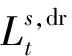
对于可削减负荷,传统需求响应补贴在调度周期内并没有划分多个交易区间,导致用户参响应的积极性不高。为更好地激发用户参与需求响应的积极性,构建了阶梯式需求响应模型,如式(16)所示。

(16)

式中:FDR为需求响应补贴收益;λdr为PLES的需求响应补贴价格;Ls,cl为调度周期内负荷削减总量;α1为需求响应价格增长幅度;l1为负荷削减区间长度。

3 PIES主从博弈模型

3.1 主从博弈框架

PIES中园区运营商和用户聚合商的博弈框架如图2所示。其中园区运营商作为PIES的调度中心,主要承担着满足用户用能需求的责任。同时,园区运营商向用户传递售能价格,并对用户实行阶梯式需求响应补贴策略,使资源得到高效利用。用户聚合商则根据运营商公布的价格自行调整自身用能需求并上报用能计划,运营商则根据用户用能计划合理安排设备出力。由于园区运营商与负荷聚合商之间存在利益博弈,而园区运营商具有供能方的优先决定权,因此,双方可以建立以园区运营商为领导者,用户聚合商为跟随者的主从博弈模型。在博弈中,当任何一方都不能通过调整决策来提高效益时,博弈达到均衡。

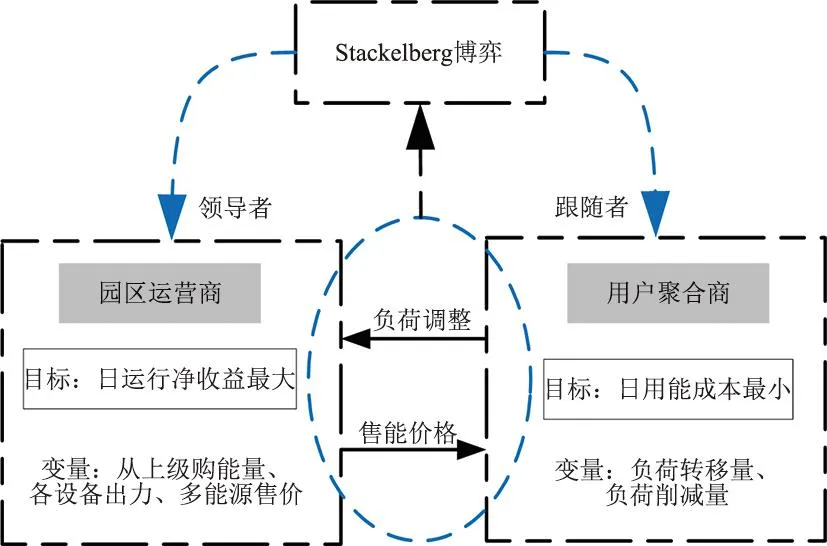
图2 主从博弈框架

3.2 园区运营商模型

园区运营商作为领导者在与用户能源交易过程中以园区运营商日运行净收益最大为优化目标,目标函数为售能收益与购能成本、设备运维成本、需求响应补贴成本之差,如式(17)—式(21)所示。

(17)

(18)

(19)

(20)

Cdr(j)=FDR(j)

(21)

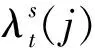
3.3 用户聚合商模型

用户聚合商作为跟随者以日用能成本最低为优化目标,目标函数为购能成本、不舒适成本与需求响应补贴收益之差,如式(22)—式(24)所示。

(22)

Csale(j)=Fsale(j)

(23)

(24)

3.4 约束条件

在PIES优化调度过程中需满足设备运行约束、功率平衡约束、购能约束以及内部价格约束,如式(25)—式(40)所示。

a.设备运行约束

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

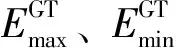
b.功率平衡约束

(36)

(37)

c.购能约束

(38)

(39)

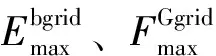
d.内部价格约束

(40)

3.5 模型求解方法与流程

本文采用遗传算法初始化、更新上层园区运营商的售能价格,下层问题利用CPLEX求解器进行求解,求解流程如下:

a.初始化园区运营商和用户聚合商的参数,k=0,设置种群规模m为30,迭代次数为100,种群变异率为5%,交叉概率为80%;

b.利用遗传算法初始随机生成m组园区运营商的售电价、售热价,并将价格参数传至用户聚合商;

c.令k=k+1;

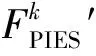
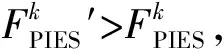
h.若k>100,则迭代结束。

4 算例分析

4.1 基础数据

本文以北方某一典型园区为算例,以一天24 h为调度周期、步长1 h来验证上述的优化调度策略。PIES中采用的分时电价如表1所示,售热价格上下限分别取0.5元/kWh和0.2元/kWh,各设备的参数如表2所示[15]。图3为考虑风光不确定性的场景削减结果,概率分别为0.245、0.190、0.125、0.125、0.315。阶梯式需求响应区间长度为60 kW,需求响应补贴价格增长率为0.3,需求响应补贴为0.24元/kWh;用户电、热不舒适成本系数分别为0.008、0.016[16]。

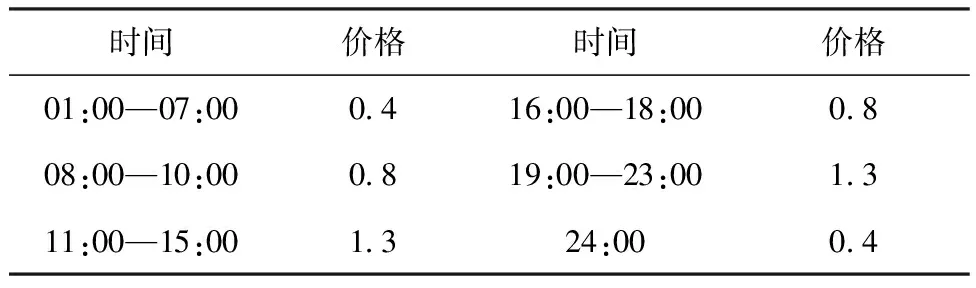
表1 分时电价 单位:元/kWh

表2 设备参数

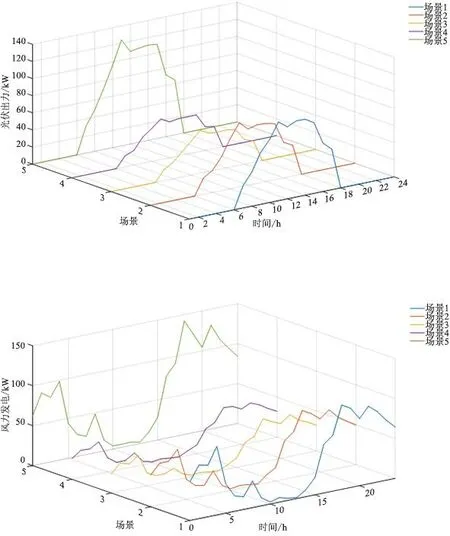
图3 5种风光不确定性场景

4.2 场景对比分析

为了验证考虑风光不确定和阶梯式需求响应对PIES主从博弈优化调度中双主体效益的影响,本文设置下列3种场景。

场景1:园区运营商侧不考虑风光不确定性,用户聚合商侧需求响应为传统补贴。

场景2:园区运营商侧不考虑风光不确定性,用户聚合商侧为阶梯式需求响应补贴。

场景3:园区运营商侧考虑考虑风光不确定性,用户聚合商侧为阶梯式需求响应补贴。

3种场景下PIES中的园区运营商和用户聚合商效益迭代计算过程如图4—图6所示,对比结果如表3所示。

根据图4—图6所示,场景1、场景2和场景3下的园区运营商和用户聚合商效益曲线都在第52次、第38次和第70次迭代时达到了收敛,这表明均衡解存在。

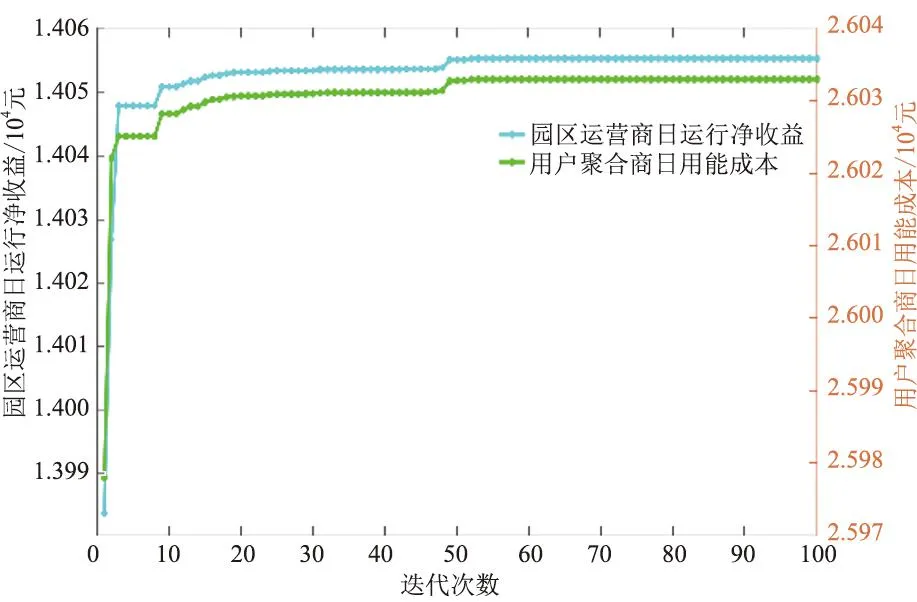
图4 场景1效益迭代图

图5 场景2效益迭代图

图6 场景3效益迭代图

比较场景2和场景1可以发现,相较于情景1,考虑阶梯式需求响应后,园区运营商日运行净收益增加814元,用户跟据购能价格积极调整负荷需求,成功减少1960元日用能成本,其中,虽然需求响应成本增加431元,但补贴获得的收益增加958元。

比较场景3和场景2,可以发现,相较于情景2,考虑风光不确定性后,园区运营商日运行净收益增加834元,用户购能成本减少1054元,用户需求响应成本增加167元但和需求响应收益增加527元。

4.3 PIES优化调度结果分析

本文以场景2为例进行分析,图7、图8分别为博弈均衡后园区运营商制定的售能价格以及对应相关信息。可以看出,园区运营商制定的价格波动趋势与其对应的用户用能趋势一致,目的是在保证系统运行经济性的前提下,兼顾下级用户的利益。

图7 电负荷优化结果

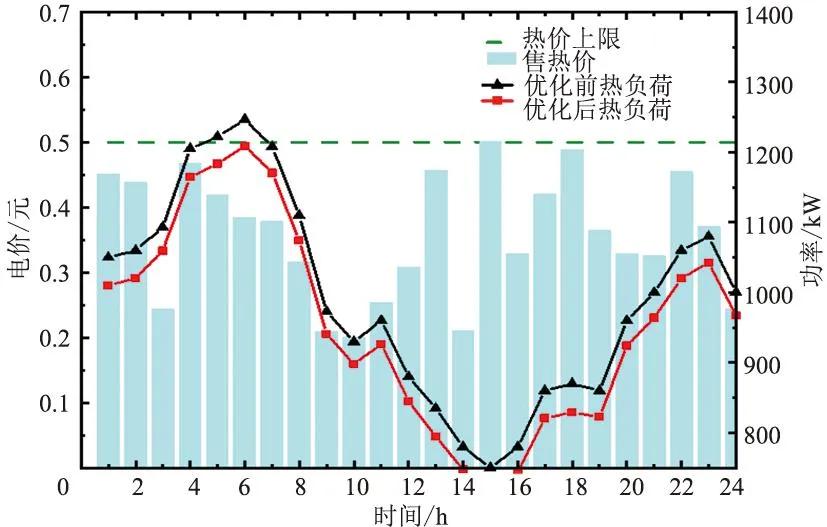
图8 热负荷优化结果

图9和图10为博弈均衡后各设备的调度结果。由于GT设备的热电联产特性以及天然气的低成本特性,因此其几乎全天处于满负荷运行状态。对于电负荷,运营商优先采用新能源出力满足用户负荷需求。并且在低电价时段,运营商选择储电并在高电价时放电从中获得收益。对于热负荷,运营商用燃气锅炉和储热罐对燃气轮机不能提供充足热量时进行补充。

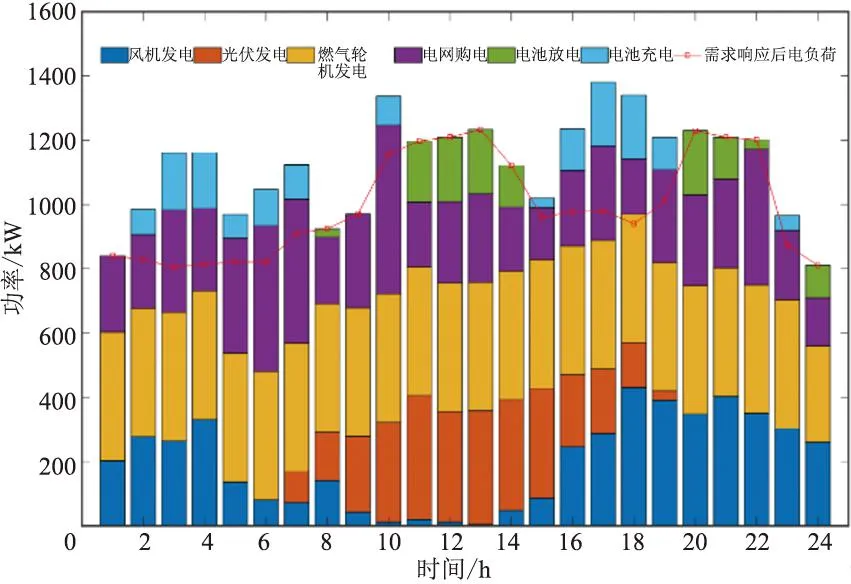
图9 电能调度

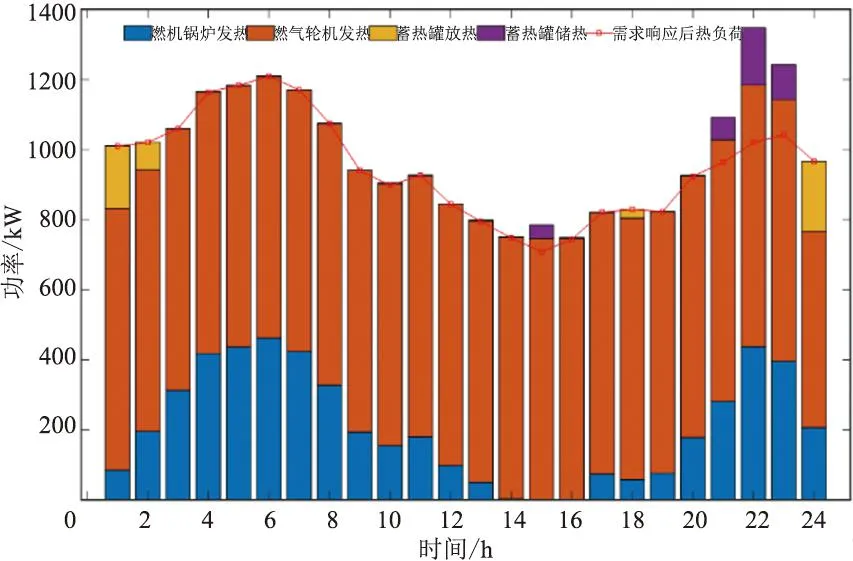
图10 热能调度

5 结论

本文针对园区综合能源系统,提出了考虑风光不确定性和阶梯式需求响应的PIES主从博弈优化调度策略,通过算例验证,得到如下结论。

a.与不考虑风光不确定性和考虑常规需求响应的供需博弈模型相比,所搭建的考虑风光不确定性和阶梯式需求响应的主从博弈模型可以提高各主体的运行效益,验证了所提模型的有效性。

b.遗传算法与CPLEX求解器结合在求解多种价格博弈时,能够有效确定博弈均衡解,且求解结果具有较好的收敛性。

在后续研究中,将进一步考虑园区综合能源系统在多时间尺度上和多园区合作博弈时对各主体运行的影响。