An improved effective liquid drop model for cluster radioactivity

JianPo Cui (崔建坡) ,FengZhu Xing (邢凤竹) ,YongHao Gao(高永浩) ,LiQian Qi (齐立倩) ,YanZhao Wang (王艳召),4, and JianZhong Gu (顾建中)

1 Department of Mathematics and Physics,Shijiazhuang Tiedao University,Shijiazhuang 050043,China

2 Institute of Applied Physics,Shijiazhuang Tiedao University,Shijiazhuang 050043,China

3 Hebei Research Center of the Basic Discipline Engineering Mechanics,Shijiazhuang Tiedao University,Shijiazhuang 050043,China

4 Hebei Key Laboratory of Physics and Energy Technology,North China Electric Power University,Baoding 071000,China

5 China Institute of Atomic Energy,P.O.Box 275 (10),Beijing 102413,China

Abstract The effective liquid drop model (ELDM) is improved by introducing an accurate nuclear charge radius formula and an analytic expression for assaulting frequency.Within the improved effective liquid drop model (IMELDM),the experimental cluster radioactivity half-lives of the trans-lead region are calculated.It is shown that the accuracy of the IMELDM is improved compared with that of the ELDM.At last,the cluster radioactivity half-lives that are experimentally unavailable for the trans-lead nuclei are predicted by the IMELDM.These predictions may be useful for searching for new candidates for cluster radioactivity in future experiments.

Keywords: cluster radioactivity,nuclear charge radius,assaulting frequency,effective liquid drop model

1.Introduction

Cluster radioactivity is an exotic decay mode observed in actinide nuclei,where the clusters emitted from the parent nuclei are heavier than α-particle and lighter than spontaneous fission fragments.So,the cluster radioactivity is also called heavy-ion radioactivity.It was first predicted by Sandulescu,Poenaru,and Greiner in 1980 [1].Four years later,cluster radioactivity was first observed experimentally through14C emitted from223Ra.Furthermore,its decimal logarithm value of the half-life was measured as 15.20 s [2].Since then,various emitted clusters have been observed,such as20O,22,24-26Ne,28,30Mg,and32,34Si [3–7].These clusters are emitted from the actinide nuclei ranging from221Fr to242Cm,while the remaining residue is the double magic nucleus208Pb or its neighborhoods [3–7].It implies that the nuclear shell effect plays a crucial role in the cluster radioactivity of the heavy nuclei.

Nowadays,various theoretical models have been developed to study the cluster radioactivity [8–34].Generally,these models are divided into the following two categories.One is the fission-like model,which means the nucleus deforms continuously as it penetrates the nuclear barrier and reaches the scission configuration after running down the Coulomb barrier [8–24].The other one refers to the preformed cluster model.It assumes that clusters have been formed in the parent nucleus before tunneling the barrier[25–34].In addition,some semi-empirical formulas or relationships have been proposed to calculate the half-lives of the cluster radioactivity [35–43].The experimental half-lives of the cluster radioactivity are reproduced more or less satisfactorily by the models and the semi-empirical formulas or relationships [8–43].

Among the models,the ELDM is a successful phenomenological model for describing the cluster radioactivity[15].In the framework of the ELDM,the cluster radioactivity is assumed as a super-asymmetric fission process [15,44–46].Besides the cluster radioactivity,one-proton emission,twoproton radioactivity,α-decay and cold fission can be described in a unified framework of the ELDM [15,44–52].In order to evaluate the half-lives of different radioactivity,the Gamow penetrability factor is obtained by considering the pre-scission phase of the two intersecting spherical fragments in the effective one-dimensional potential barrier based on four kinds of combinations of the mass transfer descriptions and the inertia coefficients.Therefore,the experimental halflives of various radioactivity could be reproduced well [15,44–52].

However,for each combination of any type of radioactivity,only two constants (the nuclear charge radius parameterr0and the assaulting frequency ν0) are adjusted to obtain the agreement with the experimental half-lives [15,44–52].As a result,the predictive power of the ELDM is not so strong,owing to the following two reasons: (i) Since the half-life of the charged-particle radioactivity is sensitive to the nuclear charge radius [53–57]a minor change will result in a large deviation of the decay half-life.So,a more accurate charge radius expression should be introduced into the ELDM instead of a simple empirical charge radius formula(R=r0A1/3).(ii)The assaulting frequency ν0should not be a constant,which may be correlated to the nuclear structure[57,58].Thus,the assaulting frequency including the nuclear structure should be introduced into the ELDM.In our previous work,the ELDM was improved by introducing an accurate nuclear charge radius formula and an analytic expression for ν0[59].It was shown that the accuracy of the IMELDM was improved evidently compared with its predecessor[59].So,in this work,we will extend the IMELDM to study the cluster radioactivity of the heavy nuclei whose daughter nuclei are around208Pb.This constitutes the motivation of this article.

This article is organized as follows.In section 2,the framework of the IMELDM is presented.The corresponding results and discussions are made in section 3.In the last section,some conclusions are drawn.

2.IMELDM

In the framework of the ELDM,the decaying nucleus is considered as two spherical molecular shape fragments of different radii in contact [15,44–52],which is shown in figure 1.

During the nuclear decaying process,four independent coordinates(R1,R2,ζ and ξ)are used to describe the dinuclear system.Then,three constraints are introduced to reduce the spherical four-dimensional problem to an equivalent onedimensional case.

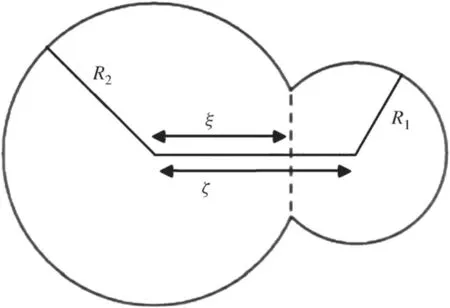
Figure 1.Schematic representation of the dinuclear decaying system.R1 and R2 show the radii of the emitted cluster and the daughter nucleus,respectively.ζ is the distance between their geometric centers.The variable ξ represents the distance between the plane of the intersection and the center of the daughter nucleus.

The first one,

keeps a circular shape for the neck connecting the nascent fragments.

The second one,

denotes the incompressibility of the nuclear flow,whereRis the radius of the parent nucleus.

The last constraint is related with the mass transfer descriptions chosen to treat the process.In the case of the varying mass asymmetry shape (VMAS),the radius of the lighter fragment is fixed as

whereR1is the final radius of the lighter fragment.In the other case of the constant mass asymmetry shape (CMAS),the volume of both fragments is kept as a constant.For the lighter fragment,volume conservation gives

Thus,the nuclear decay is conveniently simplified as the effective one-dimensional potential barrier penetrability problem.In order to evaluate the half-life of a given parent nucleus,the Gamow penetrability probability is calculated by

Table 1.Fitting parameters of equation (13).

Here,the limits ζ0and ζcof the integral are the inner and outer turning points,respectively.μ is the inertia coefficient.V(ζ) is the one-dimensional total potential energy and given as

whereVC(ζ),VS(ζ) andVl(ζ) represent the Coulomb energy,effective surface energy and centrifugal potential energy,respectively.The analytic expression and details of them can be seen from [15,44,46].Qcdenotes the decay energy and is calculated by the following relation:Qc=M(Z,N)-Md(Z-Zc,N-Nc)-M(Zc,Nc),whereM(Z,N),Md(Z-Zc,N-Nc) andM(Zc,Nc) represent the mass excesses of the parent nucleus,daughter nucleus and emitted cluster,respectively.In the ELDM,two approximations are used to calculate the inertia coefficients of the dynamical evolution of the separating dinuclear system.The two types of inertia coefficients are the Werner-Wheeler’s inertia coefficient(WW) and the Effective inertia coefficient (Eff).Combining two mass transfer descriptions and two inertial coefficients,the following four kinds of descriptions: (VMAS,WW),(VMAS,Eff),(CMAS,WW),and(CMAS,Eff)are contained naturally in the ELDM.For each description,the radius parameterr0together with ν0are determined to be constants by fitting the experimental data.The values of these parameters can be seen in table A of [46].

The charge radius of the parent nucleus is obtained by

whereAis the mass number of the parent nucleus.

For the half-life of the cluster radioactivity,it is calculated by

However,the parent nuclear radius by equation(7)is not accurate enough,which has been tested by relevant studies[54].Meanwhile,ν0is correlated to the structure of the nuclei and should not be a constant.Therefore,a more accurate formula forRand a more reasonable ν0are necessary to be introduced into the ELDM.

In the next paragraphs,we will describe the details of the IMELDM.Firstly,equation (7) is replaced by a five-parameter formula to estimate more accurateRvalues [54]

whereKand δ represent the Casten factor and the odd–even staggering factor,respectively.The parametersr0,a,b,canddcan be found from table 1 of [54].

Combining equations (5) and (9) the penetration probabilityPcan be estimated.Then the empirical value of ν0for each nucleus can be extracted by the following expression

Usually,the values of ν0are calculated by the following classic method

wherevis the velocity of the cluster inside a parent nucleus.Ec(Ec=[(A-Ac)/A]Qc),AcandMcrepresent the kinetic energy,the mass number of the emitted cluster and the atomic mass of the emitted cluster,respectively.Its decimal logarithm form is written as

BecauseMc=Acu,hereuis the atomic mass unit,based on equation (12) a simple analytic expression for ν0is expressed as

where the parametersa′,b′,c′,andd′ are determined by the following steps: (i) 20 experimental pieces of data of cluster radioactivity are divided into even-even and odd-Asubsets,which are taken from[4,60,61].(ii)Using the multiple linear regression,the parametersa′,b′,c′ andd′ for each combination of each subset are determined by fitting the empirical ν0values extracted from equation (10).They are listed in table 1.At last,combining equations (5),(9),and (13),the cluster radioactivity half-life is calculated by equation (8).

3.Results and discussion

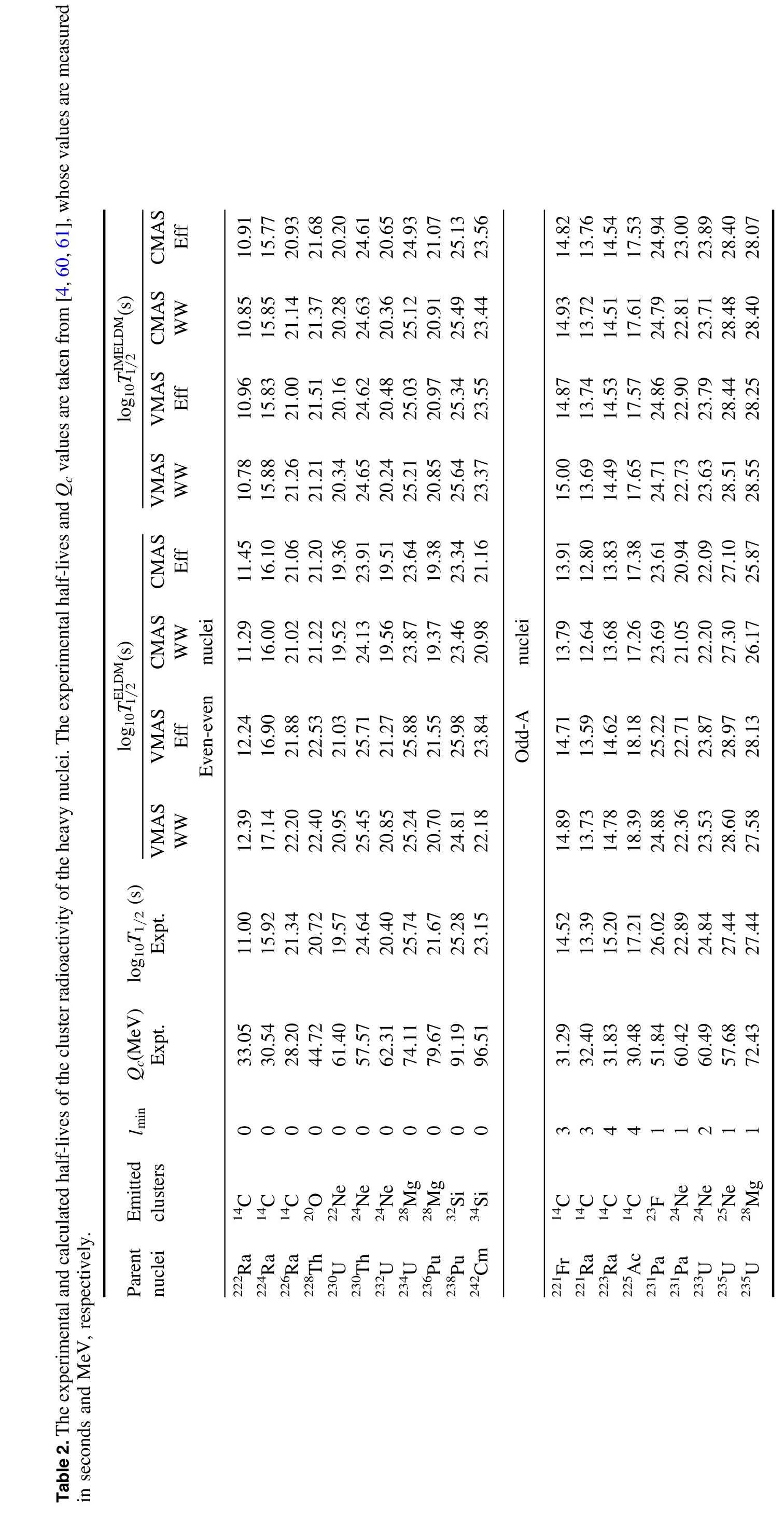
Table 3.The average deviation and the standard deviation between the experimental and calculated half-lives of the cluster radioactivity for each combination of the ELDM and IMELDM.

Table 3.The average deviation and the standard deviation between the experimental and calculated half-lives of the cluster radioactivity for each combination of the ELDM and IMELDM.

Within the IMELDM,the half-lives of ground-state to ground-state cluster radioactivity of 20 nuclei have been calculated by inputting the experimentalQcvalues and the minimum angular momentalmincarried by the emitted clusters.Note that thelminvalues are determined by the spinparity selection rule.The calculated results are listed in table 2.From table 2,the first three columns indicate the parent nuclei,the emitted clusters and the minimum angular momenta,respectively.The fourth and fifth columns give the experimentalQcvalues and the decimal logarithms of cluster radioactivity half-lives[4,60,61].The sixth to ninth columns show the calculated cluster radioactivity half-lives for each combination within the ELDM.In the last four columns,the cluster radioactivity half-lives of each combination within the IMELDM are listed.From table 2,it is seen that the results by the IMELDM are closer to the experimental data than those by the ELDM.

To further test the agreement between the calculated results and the experimental data,the average deviationand the standard deviationare calculated by the following expressions

From table 3,it is seen that thevalues within the IMELDM are much smaller than those within the ELDM.For each combination,thevalues within the IMELDM decrease to about 0.50 (0.60) from largevalues.Especially,for the (CMAS,Eff) combination,thevalue within the IMELDM decreases to 0.480 (0.579) from 1.165 (1.444),which implies the accuracy of the ELDM increases by 59% (60%).Therefore,the accuracy of the IMELDM becomes much higher than that of the ELDM by introducing more reasonable analytic expressions forRand ν0.

Usually,it is believed that if thelog10HFvalue is within a factor of 1.0,the calculated half-lives will be in agreement with the experimental data[47,59,62].Within equation(16),thelog10HFvalues for the (VMAS,WW),(VMAS,Eff),(CMAS,WW)and (CMAS,Eff) combinations of the ELDM and IMELDM are calculated.Thelog10HFvalues versus the neutron numberNof the parent nuclei are plotted in figure 2.From figure 2,one can see that morelog10HFvalues within each combination of the IMELDM fall between -1.0 and 1.0.So the conclusion based on figure 2 is the same as that from table 3.

Table 4.The empirical values of ν0 extracted by equation(10)and the fitting ones by equation(13)within the(CMAS,Eff)combination of the IMELDM.

From the perspective of ν0,we know that the accuracy of the IMELDM depends on the agreement between the empirical ν0values and the fitting ones.To illustrate why the accuracy of the IMELDM becomes higher,the empirical and fitting ν0values of the (CMAS,Eff) combination are shown in the last two columns of table 4.From table 4,good agreement between the empirical ν0values and the fitting ones can be found.As a result,the half-lives estimated from the IMELDM are closer to the experimental data.Moreover,as can be seen from table 4,the log10ν0values decrease with the increase of the mass of the emitted cluster.In fact,the cluster preformation probability inside a parent nucleus is included in ν0in the framework of the IMELDM.The heavier the emitted cluster,the smaller the cluster preformation probability inside a parent nucleus.So the heavier cluster has a smaller log10ν0value naturally.In addition,we know that the ν0values that do not contain the preformation probabilities can be estimated by equation (11).Thus the cluster preformation probabilities can be estimated by the ratio between the empirical ν0(fitting ν0)values and the calculated ν0values within equation (11).By taking221Ra →207Pb+14C and231Pa →207Tl+24Ne as examples,we obtain the14C and24Ne preformation probabilities,whose values are 7.88×10-2and 3.69×10-4,respectively.

By consulting [4,60],it is found that for the cluster radioactivity of several heavy nuclei,only the lower limits of the half-lives were measured.Thus,those experimental data constitutes a ground to test the IMELDM.The above discussion suggests the accuracy of the (CMAS,Eff) combination is improved most evidently.So,the (CMAS,Eff)combination is used to calculate the cluster radioactivity halflives in this case.The experimental half-lives with a lower limit and the calculated half-lives within the ELDM and IMELDM are shown in table 5.From table 5,it can be seen that all the calculated half-lives within the IMELDM are larger than those within the ELDM.For226Th,232U and240Pu,the half-lives within the ELDM and IMELDM are larger than the corresponding experimental lower limits.For233U,237Np and241Am,as can be seen from table 5 the experimental halflives are not reproduced well within the ELDM.However,thehalf-lives within the IMELDM are closer to or in agreement with the experimental data compared to those within the ELDM.

Table 5.The calculated half-lives of cluster radioactivity within the(CMAS,Eff)combination of the ELDM and IMELDM,for those cases in which the lower limits of the experimental half-lives were measured.

Table 6.The calculated partial half-lives and the total half-lives of two types of clusters from the same parent nucleus within the(CMAS,Eff)combination of the ELDM and IMELDM.The experimental half-lives and the Qc values are taken from [4,60,61].

In addition to the experimental data of table 5,from[4,60] it is found that there exist two kinds of cluster radioactivity for234,236U,238Pu and232Th.For example,24Ne and26Ne can be emitted simultaneously from234U.Although the experimental half-life of each kind of cluster radioactivity has not been determined,the total half-lives or the lower limits of the total half-lives for the two types of cluster radioactivity were given [4,60].Thus,these experimental half-lives provide alternative grounds for testing the IMELDM.Generally,the angular momentalcarried by the clusters are selected as 0,being only a weak impact on the cluster radioactivity half-lives [33,43].To show the relationship betweenland the half-life,the decimal logarithms of half-lives for221Ra →207Pb+14C and231Pa →207Tl+24Ne as functions oflare plotted in figure 3.From figure 3,it is seen that the decimal logarithms of half-lives of the two emissions grow by 0.28 and 0.15 whenlrises from 0 to 5.So,the cluster radioactivity half-lives are indeed slightly affected byl.For the centrifugal potential,it is a small quantity compared to the Coulomb barrier,the Gamow penetration probability is almost unchanged when the centrifugal potential is taken into account.Thus,lvalues are selected as 0 in the subsequent calculations.The calculated half-lives within the (CMAS,Eff) combination of the ELDM and IMELDM are listed in table 6.In table 6,the parent nuclei and the emitted two types of clusters are listed in the first two columns.The experimentalQcvalues of each kind of cluster radioactivity are listed in column 3.By inputting the experimentalQcvalues,the partial half-lives and the total half-lives of the two types of cluster radioactivity are calculated within the ELDM and IMELDM,which are listed in columns 4-7.The experimental total half-lives are listed in the last column.From the last three columns of table 6,it is seen that the experimental total half-lives are reproduced better within the IMELDM than those within the ELDM.Therefore,by the discussion of tables 3–6,we can conclude that the IMELDM is a successful model for estimating the cluster radioactivity half-lives of the heavy nuclei.

Encouraged by the agreement mentioned above,within the(CMAS,Eff)combination of the IMELDM we attempt to predict the cluster emission half-lives that have not yet been available.The cluster radioactivity half-lives of8Be,12,14C,15N,16-20O,20-26Ne,24-28Mg,and30-34Si emitted from the heavy nuclei in the trans-lead region are predicted,which are listed in table 7.We hope these predictions are helpful for searching for new cluster emitters in future experiments.

4.Conclusions

In this article,the ELDM has been improved by introducing an accurate formula forRand an analytic expression for ν0,which is called the IMELDM in the article.Within the IMELDM,the experimental cluster radioactivity half-lives of 20 nuclei in the trans-lead region are calculated.It is shown that the accuracy of the IMELDM becomes much higher than that of the ELDM.Next,the IMELDM has been tested by the experimental cluster radioactivity half-lives with lower limits and the experimental total half-lives with two types of cluster radioactivity from the same parent nuclei.It indicates that the IMELDM is a successful model for studying the cluster radioactivity of the heavy nuclei.Then,the (CMAS,Eff)combination of the IMELDM is adopted to predict the cluster radioactivity half-lives of the heavy nuclei in the trans-lead region.These predictions may be helpful for searching for new candidates for cluster radioactivity in future experiments.Finally,it is necessary to point out that the proton radioactivity is an important decay mode for the extremely protonrich nuclei [51,52,62–66].So it is interesting to extend our approach to study the proton radioactivity,which is underway.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos.U1832120 and 11675265);S&T Program of Hebei (Grant No.236Z4601G);Scientific Research Foundation for the Introducing Returned Overseas Chinese Scholars of Hebei Province(Grant No.C20230360);Natural Science Foundation for Outstanding Young Scholars of Hebei Province (Grant No.A2020210012);Natural Science Foundation of Hebei Province (Grant No.A2021210010);Key Laboratory of High Precision Nuclear Spectroscopy,Institute of Modern Physics,Chinese Academy of Sciences (Grant No.IMPKFKT2021002) and Key Project of Natural Science Foundation for Basic Discipline Research of Hebei Province (Grant No.A2023210064).