基于ISMM方法的非均匀磁化等离子体湍流中电磁波传播特性研究

2024-04-02陈伟马琪琪杨利霞薄勇

电波科学学报 2024年1期

陈伟马琪琪杨利霞* 薄勇

（1.安徽大学电子信息工程学院, 合肥 230601；2.目标探测与特征提取安徽省重点实验室, 合肥 230601；3.先进激光技术安徽省实验室，合肥 230601）

0 引言

高超声速飞行器在飞行的过程中会与空气发生摩擦，使飞行器周围温度急剧升高，导致气体电离形成等离子体流场。受飞行器气动外形和飞行速度的影响，等离子体流场中会产生多个形状和大小不等的涡旋结构，称为等离子体湍流[1]。这些湍流混杂在等离子体流场中会严重干扰电磁波的传播，影响通信性能和通信质量[2]。

为了解决黑障问题，国内外对电磁波在等离子体鞘套中的传播特性做了大量的研究。2016年，李江挺等人基于风洞实验中获得的超声速湍流图像，得到了折射率起伏能谱，并建立模型求解了结构函数和空间相干长度，同时获得了高超声速湍流对于电磁波传输的影响[3]。2019年，Chen等人开展了基于一维湍流（one-dimensional turbulence，ODT）模型的建模与数值模拟方法研究[4]。围绕电磁波与等离子体鞘套相互作用问题，研究人员使用了时域有限差分（finite-difference time-domain, FDTD）法[5-6]、温泽尔-克莱默-布里渊法(WKB)[7]，以及散射矩阵法（scattering matrix method, SMM）[8]等方法。Chen与Zhang等人基于改进的SMM（improved SMM, ISMM）分析了电磁波在非均匀等离子中的传播特性[9-10]，薄勇等人基于FDTD开展了非均匀磁化等离子体鞘套中的传输特性研究[11]。近年来，针对等离子体外部磁场对电磁波在等离子体鞘套传播特性影响的研究开展了一系列的计算仿真，其中磁化特性主要包括磁化均匀、磁化非均匀[12]、动态磁化[13]、非磁化均匀[14]和非磁化非均匀[15]等，宫卫华等人基于实验研究了非均匀磁场尘埃等离子体中颗粒的复杂运动[16]，以上结果表明研究等离子体鞘套中湍流以及磁化的存在对电磁波传播特性的影响，为解决黑障问题提供了理论指导，因此，开展电磁波与非均匀磁化等离子体之间的传播特性研究，对于解决带有湍流的磁化等离子体鞘套环境的通信问题十分重要。

为了更加全面地探究磁场对电磁波在等离子体湍流中传输特性的影响以及解决SMM奇异矩阵的问题，本文采用ISMM，从不可压缩的一维简化NS方程的对流项和扩散项出发，通过在物理模型中增添涡流的变化，深入分析等离子体湍流对圆极化电磁波传播特性的影响。

1 ODT磁化等离子体模型理论推导

ODT模型沿着z方向分布，其不可压缩的一维简化N-S方程如下[17]：

式中：v是电子速度；ρ是流体密度；P是压力；f是外部合力；µ是粘性系数。

式中：e是电子电荷量；me是带电粒子的质量；E和B分别是对应的外部电场和磁场；ven是等离子体碰撞频率。

感应电流

由欧姆定律J=σE与麦克斯韦方程[18]

可得磁化等离子体的介电常数

式(4)~(7)中：net(z)是电子密度关于距离飞行器表面z处的分布函数；σ是点电导率；ω是入射波的频率；ε0是真空中的介电常数；ωce=e|B|/me是电子产生的电子回旋频率；“+”表示右旋圆极化，而“-”表示左旋圆极化[19]。

由等离子体压力与电子密度关系PM=ρRT可得

式中，摩尔质量M、气体常数R与温度T均是常量，可得磁化等离子体鞘套中速度梯度的变化与电子密度变化近似呈线性关系。

考虑等离子体是无粘流体，湍流可以看成平稳随机过程，其电子密度分布函数为[20]

添加涡流变化后，有

式(10)~(12)中：nemax是电子密度峰值；α=0.01是层流空间变化率；∆β=0.005是涡流变化系数；ft(z)是均值为0、方差为1的标准正态分布随机变量函数；L是电子密度波动变化度。式（11）所示的粒子密度的变化是由涡事件的发生导致的，且其前后变化的总粒子数近似不变，即

由25 km高度、9马赫速度飞行下一维等离子体湍流模型（图1，其中Zn代表等离子体鞘套距离飞行器表面第n层）可知等离子中电子密度变化规律：在涡流边界区域的波动小于中心区域且前后总电子数量近乎不变，图(a)中电子密度峰值为1×1019数量级，图(b)中电子密度峰值同样为1×1019数量级。高度25 km时最大电子密度随马赫数变化规律如图2所示[21]。

图1 一维等离子体湍流模型Fig.1 One-dimensional plasma turbulence model

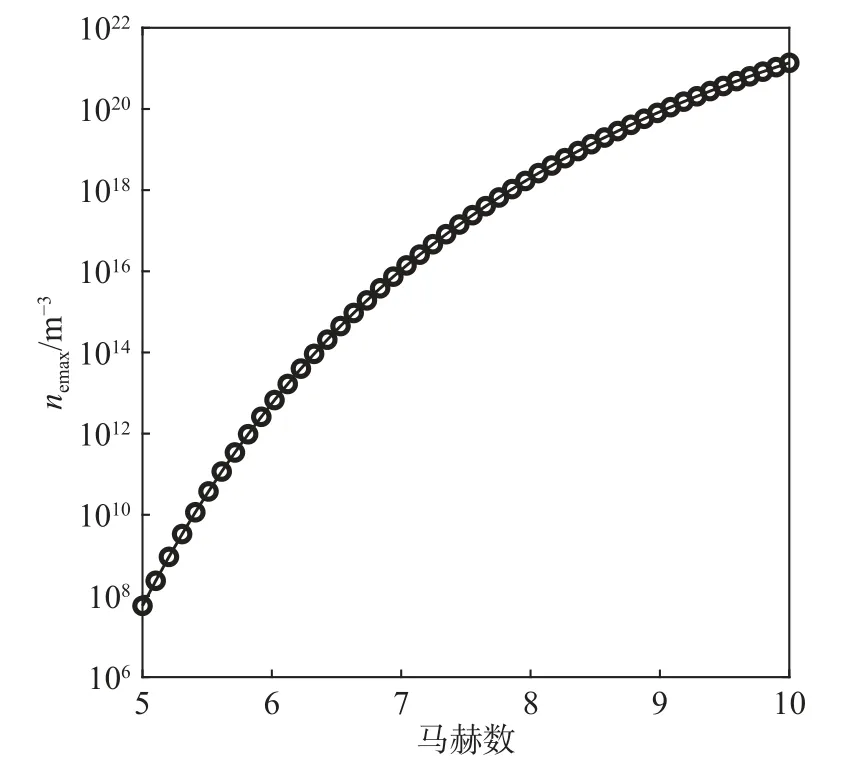
图2 最大电子密度随马赫数变化图Fig.2 Plot of maximum electron density as a function of Mach number

2 ISMM

对于电子密度非均匀分布的等离子体可以视为由n层的等离子体薄片构成（如图3所示），每层电子密度分布与ODT模型一致，电磁波垂直或斜入射等离子体鞘套时，第km层的传播常数k(m)可以表示如下[22]：

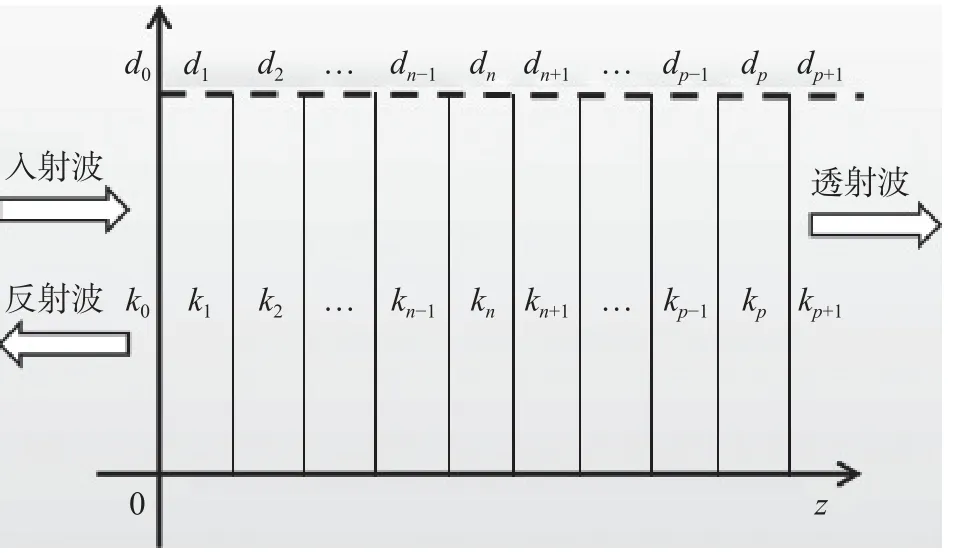
图3 电磁波在层状等离子体中的电磁波传播示意图Fig.3 Schematic of electromagnetic wave propagation in a layered plasma

式中：c是光在自由空间的传播速率；是第m（m=0,1）层复介电常数。区域(k0)中的入射电磁场可以分别表示为：

匹配z=0层处的边界条件可写成

与SMM每个等离子体层的参考点为前一层不同，将每相邻两个等离子体层的参考点统一设置为入射表面，有

类似地，对第m层边界进行匹配并化简可得：

转化为矩阵为

在最后一个层，只有透射波，用T表示总的透射系数，同理使用z=kp的边界条件进行匹配转化为矩阵有

将方程（18），（22），（24）重新整理为

式中：Sg1和Sg2分别是矩阵Sg的第一个和第二个列向量。分层介质板的反射系数和透射系数可用分贝表示如下：

基于ODT模型电子密度计算透射系数结果，由图4可知：在0~20 GHz范围内，SMM数值波动更大，会出现跳变的点，这种现象会导致在一定范围内对电磁波传播特性的计算不准确；ISMM计算的传播特性在整个入射频率范围内都是平滑的，说明ISMM在分析等离子体湍流的传播特性方面具有更好的鲁棒性。

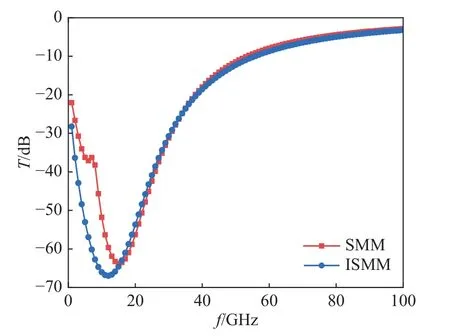
图4 基于ODT模型SMM与ISMM透射系数对比图Fig.4 Comparison of transmission coefficients between SMM and ISMM method based on ODT model

如图5所示，随着飞行速度的增大，等离子体鞘套的最大电子密度随之增加，使得在高频区间(50~100 GHz)的反射系数增大，低频区间(0~45 GHz)的透射系数减小[21].

图5 飞行速度对等离子体反射系数和透射系数的影响Fig.5 The influence of different flight speeds on the reflection coefficient and transmission coefficient of plasma

当α=0.01，涡流变化率∆β分别为0与0.01时的电磁波传播特性如图6所示，无论有无湍流，等离子体的反射系数随着入射波频率的增大均呈现出一种规律性震荡递减的现象，这是由于入射波在介质层表面进行多次反射形成。在低频区域(0~35 GHz)，电磁波的电场必然会对自由电子进行加速，而加速的电子在运动过程中将能量转化为热能，导致能量的衰减进一步增多，促进了电磁波的能量转化为湍流的内能，严重阻碍了电子的德拜屏蔽作用，因此电磁波在带有湍流的等离子体鞘套中的透射系数也就增大了。

图6 基于ISMM有无湍流的反射系数与透射系数Fig.6 Reflection coefficient and transmission coefficient with or without turbulence based on ISMM method

3 数值模拟结果

在利用ISMM分析电磁波传播特性时，选取等离子体层厚度为0.1 m，共分为100层，每一层的厚度为0.001 m，ne取1×1019m-3，碰撞频率为20 GHz，飞行速度8 马赫。磁场方向沿着电磁波传播方向，分别计算了左旋圆极化和右旋圆极化波不同外加磁场和入射角情况下的反射和透射系数，结果如图7、8所示。

图7 磁场强度对均匀磁化等离子体反射系数和透射系数的影响Fig.7 Influence of different magnetic field intensity on homogeneous magnetized plasma reflection coefficient and transmission coefficient

由图7可知：左旋圆极化波随着磁场强度的增大，在50~100 GHz频段范围内，电磁波的反射系数增大，而在20~50 GHz频段内的透射系数减小，并且透射系数最小频率点随着磁场强度增大而增大；右旋圆极化波的传播特性与之相反，这是因为磁场强度的增加引起回旋共振的频带向高频端偏移，左旋圆极化波的旋转方向与电子的旋转方向相同，进而在高频端产生更多的能量吸收，而对于右旋圆极化波旋转相反，导致传输功率会随外加磁场强度的增加而降低。

从图8结果可知，当磁场强度为0.5 T时，随着入射角度的变化，右旋圆极化波和左旋圆极化波在0~50 GHz频段内的透射系数产生了不同的变化趋势。这是因为等离子体中的电子受到磁场作用并做回旋运动，而右旋圆极化波的旋转方向与电子旋转方向相反，导致碰撞效应降低，有利于电磁波在等离子体中的传播。

图8 入射角对均匀磁化等离子体反射系数和透射系数的影响Fig.8 Influence of different incident angles on reflection coefficient and transmission coefficient of homogeneous magnetized plasma

为了更进一步分析磁场对电磁波传播特性的影响，这里重点分析非均匀磁场情况下入射角对电磁波传播特性的影响。非均匀磁场的强度随距飞行器表面距离的变化关系如图9所示[11]，计算结果如图10所示。

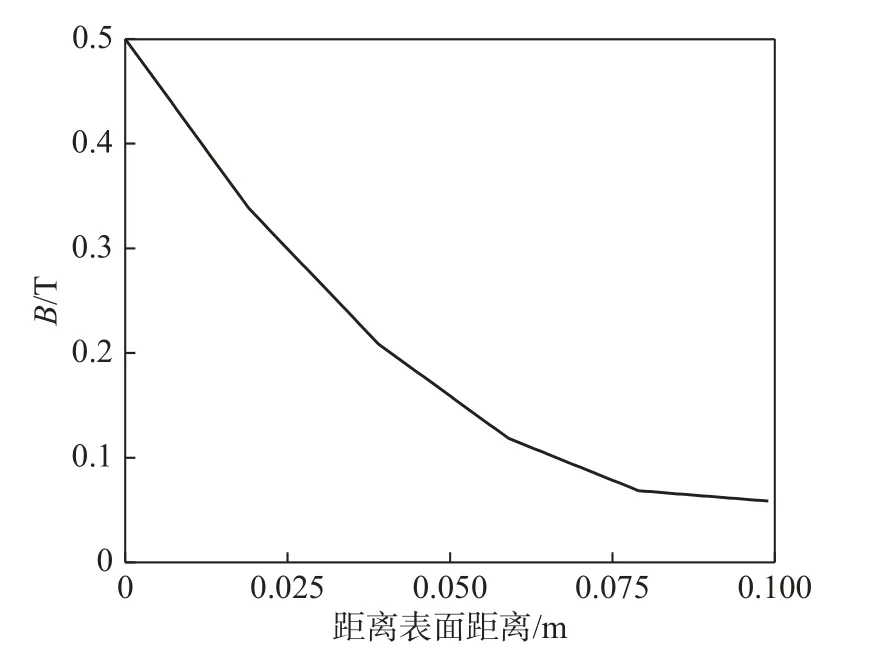
图9 磁场强度随距离分布Fig.9 Actual magnetic field intensity distribution with distance

图10 入射角对非均匀磁化等离子体反射系数和透射系数的影响Fig.10 Influence of different incident angles on reflection coefficient and transmission coefficient of inhomogeneous magnetized plasma

从图10与图8结果对比可知，当入射波频率小于30 GHz时，对于考虑非均匀磁场的等离子湍流介质，右旋圆极化波透射系数大于均匀磁场的情况。发生该现象的主要原因是右旋情况下，波的旋转方向正好与电子的旋转方向相反[23-24]，磁场强度的非均匀性导致碰撞效应减弱，同时磁化等离子体中的其他粒子由于非均匀磁场与湍流的存在有利于电磁波振荡，导致衰减减弱。当入射波频率大于70 GHz时，磁场强度对电磁波的影响可以忽略不计。