非对称集中荷载下无腹筋RC 梁受剪性能试验研究

2024-03-31袁健刘家栋段绍伟

湖南大学学报（自然科学版） 2024年3期

袁健，刘家栋，段绍伟

（中南林业科技大学土木工程学院，湖南长沙 410004）

非对称集中荷载作用下的钢筋混凝土简支梁，同一根梁中存在两个不同的剪跨比.其中，小剪跨段分担的剪力作用较大并具有较高的受剪承载力，大剪跨段受剪承载力较低且剪力作用较小.Brown 等［11］开展了非对称集中荷载作用下4 根钢筋混凝土有腹筋简支梁剪切破坏试验，每根梁的小剪跨比为1.7，大剪跨比取值范围为3.0～5.8.当梁中两个剪跨比分别为1.7 和5.8 时，小剪跨段分担的剪力是大剪跨段的3.4 倍.作者预估该梁在小剪跨段发生剪切破坏，而试验结果却恰恰相反.此外，其余3 根梁也均在大剪跨段发生剪切破坏.由此可见，尽管小剪跨段承担的剪力较大，但以混凝土斜压杆传递剪力的方式会使小剪跨段具有更高的承载力.然而，梁中各剪跨段受剪承载力与剪力作用之间的相对大小存在不确定性，发生剪切破坏的位置尚不明晰，相关试验研究也鲜见报道.

Brown 等的试验研究中箍筋作用与剪跨比两个影响因素交织在一起，在一定程度上不利于直观地揭示问题的本质.为此，本文开展6 根非对称和4 根对称集中荷载作用下钢筋混凝土无腹筋简支梁的受剪性能试验研究，并分析GB 50010—2010、修正压力场理论（简称“MCFT 公式”）［12-13］、基于截面应变分析的抗剪模型（简称“Choi 公式”）［14-15］和Zsutty 统计公式的适用性.

1 试验概述

1.1 试件设计

本试验共设计10 根钢筋混凝土无腹筋简支梁试件，梁截面尺寸均为200 mm×400 mm，截面有效高度为360 mm.梁底部配置3 根直径为22 mm 的HRB400 级纵向受拉钢筋，配筋率为1.58%.其中，6根梁采用非对称加载方式，4根梁在跨中施加集中荷载作为对比.为加强梁端纵筋的锚固效果，所有试件的纵筋在支座以外弯起并配置箍筋.试件的具体设计参数见图1和表1.表1中，基于梁的极限承载力试验值Pu，利用力学平衡关系计算得到大、小剪跨段承担的剪力分别为VW和VE.

图1 试件截面尺寸及配筋（单位：mm）Fig.1 Cross-sectional size and reinforcement of specimens（unit：mm）

1.2 材性试验

为了尽可能保证所有试件的混凝土强度相同，采用强度等级为C35 的商品混凝土，粗骨料最大粒径为26.5 mm.浇筑试件过程中，制作12 个边长为150 mm 的混凝土立方体试块，并与试件同条件养护至试验阶段.按照《混凝土物理力学性能试验方法标准》（GB/T 50081—2019）［16］的规定，以0.5 MPa/s的加载速率实测得到混凝土立方体抗压强度平均值fcu，m=42.8 MPa.采用《混凝土强度检验评定标准》（GB/T 50107—2010）［17］的非统计方法进行评定，可取混凝土立方体抗压强度的标准值为37.2 MPa，将其代入GB 50010—2010 中相关公式可计算得到混凝土的弹性模量Ec=3.19 × 104N/mm2.按照《金属材料拉伸试验第1部分：室温试验方法》（GB/T 228.1—2010）［18］的相关规定，实测得到纵向受拉钢筋的屈服强度为422 MPa.根据GB 50010—2010 取钢筋的弹性模量Es=2.0 × 105N/mm2，计算得到相应的屈服应变为2 110 με.

1.3 加载方式和测量内容

试验采用液压千斤顶施加集中荷载，AB 系列试件加载点位于试件跨中偏东，B 系列试件加载点位于试件的跨中处，加载装置示意图如图2 所示.其中，加载点处钢垫块及支座宽度均为80 mm.需要说明的是，本文确定剪跨比时未考虑钢垫块及支座宽度的影响.试验前进行预加载，检查各采集仪器是否正常工作.正式加载过程中，根据预估破坏荷载进行分级加载，每级荷载增量为预估破坏荷载的1/10；完成加载后持荷5 min，及时描绘裂缝、量测裂缝宽度并记录数据；接近破坏时，每级荷载增量调整为5 kN，加载直至试件破坏.

图2 试验装置示意图Fig.2 Schematic diagram of test set-up

在跨中和支座处布置数显位移计，用于测量梁跨中处的位移及支座处的沉降.千斤顶施加的荷载直接通过压力传感器读取，并采用DH3821静态应变仪采集应变数据.纵向受拉钢筋表面应变片的布置情况，如图3所示.

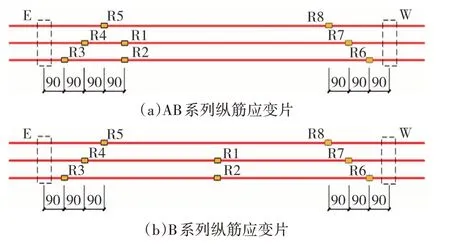
图3 纵向受拉钢筋应变测点布置（单位：mm）Fig.3 Layout of strain measuring points for longitudinal tensile reinforcement（unit：mm）

2 试验结果及分析

2.1 破坏形态

试件破坏形态如图4所示，主要试验结果见表1.其中，参照文献［19］判定试件AB1.0-1.5发生了混凝土劈裂破坏；试件AB1.0-3.5、AB1.0-4.0 和B-3.0 发生斜拉破坏，而其余试件发生剪压破坏.

实时数据库是MCGS应用系统的数据处理中心。系统各个部分均以实时数据库为公用区交换数据，实现各个部分协调动作。在本项目中，实时数据库中主要包括状态监控和参数设置两大类，需要将所有用到的数据创建出来。

图4 试件破坏形态Fig.4 Failure modes of specimens

1）劈裂破坏.试件AB1.0-1.5具有显著的深梁剪切破坏特征，破坏前大剪跨段已形成贯通的斜裂缝，但由于试件整体延性较高而未立即发生剪切破坏.随着荷载的进一步增大，梁的小剪跨段上表面距加载点0.5h0处产生劈裂裂缝而导致破坏.

2）剪压破坏.试件破坏之前，试件AB1.0-2.0、AB1.0-2.5、AB1.0-3.0 和B-1.5、B-2.0、B-2.5 均形成了明显的临界斜裂缝，但未立即发生剪切破坏.随着荷载的进一步增大，试件最终发生剪压破坏.

3）斜拉破坏.接近极限荷载时，试件AB1.0-3.5、AB1.0-4.0中大剪跨段的斜裂缝以及试件B-3.0中的临界斜裂缝仅发展至梁高一半处，随后试件突然发生剪切破坏，具有显著的斜拉破坏特征.其中，试件AB1.0-3.5 和AB1.0-4.0 中大剪跨段靠近支座处的混凝土保护层出现撕裂破坏现象.

结合图4（a）和表1 可知，试件AB1.0-1.5 在小剪跨段发生劈裂破坏，其余AB 系列试件的剪切破坏均发生在大剪跨段.当AB 系列试件的大剪跨比为2.0～3.0 时，梁的极限荷载和大剪跨段承受的剪力均随大剪跨比的增大而降低，故可判定其在大剪跨段形成临界斜裂缝并最终导致梁发生剪切破坏.尽管试件AB1.0-3.5 和AB1.0-4.0 最终在大剪跨段发生斜拉破坏，但两者的极限承载力分别比试件AB1.0-3.0 高11.5%、11.1%，小剪跨段承担的剪力非常接近且均高于试件AB1.0-3.0.由此可见，试件AB1.0-3.5 和AB1.0-4.0的极限承载力主要由小剪跨段控制.

2.2 裂缝发展

所有试件达到极限荷载的30%左右时，加载点正下方出现弯曲裂缝并逐渐向上延伸；当达到极限荷载的50%左右时，基本上不再产生新的竖向弯曲裂缝.随着荷载继续增大，最外侧的竖向弯曲裂缝逐渐倾斜并向荷载作用点延伸.其中，AB 系列试件先在小剪跨段产生斜裂缝.B 系列试件发生破坏之前，两剪跨段的裂缝基本上呈对称分布状态，发生剪切破坏的区段具有随机性.其中，试件B-3.0 的裂缝发展过程如图5（a）所示.

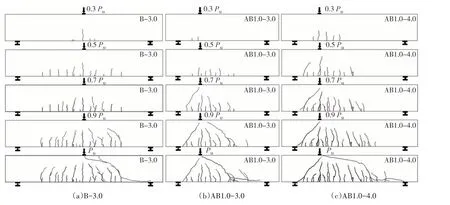
图5 裂缝发展过程Fig.5 Crack development processes

试件AB1.0-3.0 的裂缝发展过程，如图5（b）所示.当加载至极限荷载的30%时，大剪跨段未出现竖向弯曲裂缝.当加载至极限荷载的70%时，小剪跨段先形成几乎贯穿整个梁高的斜裂缝.当加载至极限荷载的90%时，大剪跨段形成了新的斜裂缝并最终发展为临界斜裂缝而导致梁发生剪切破坏.

对于试件AB1.0-3.5 和AB1.0-4.0，当加载至极限荷载的90%时，小剪跨段的斜裂缝已完全形成，而大剪跨段仍未出现明显的斜裂缝.当达到极限荷载时，大剪跨段突然出现斜裂缝而导致梁发生斜拉破坏.其中，试件AB1.0-4.0 的裂缝发展过程如图5（c）所示.

2.3 荷载-跨中位移曲线

试件的荷载-跨中位移曲线，如图6 所示.结合表1 和图6 可知，对于AB 系列试件，当大剪跨比由1.5 增大至3.0 时，梁的极限承载力呈降低趋势；小剪跨段承担的剪力呈现先降低后提高的趋势，其拐点出现在大剪跨比为2.5 处.当大剪跨比由3.0 增大至3.5 时，梁的极限承载力及小剪跨段承担的剪力提高幅度较大.由于试件AB1.0-3.5 和AB1.0-4.0 的极限承载力主要受小剪跨段控制，故两者的极限承载力非常接近且均高于试件AB1.0-3.0.AB 系列试件中大剪跨段承担的剪力随大剪跨比的增大而降低，这与B系列试件的变化规律类似.

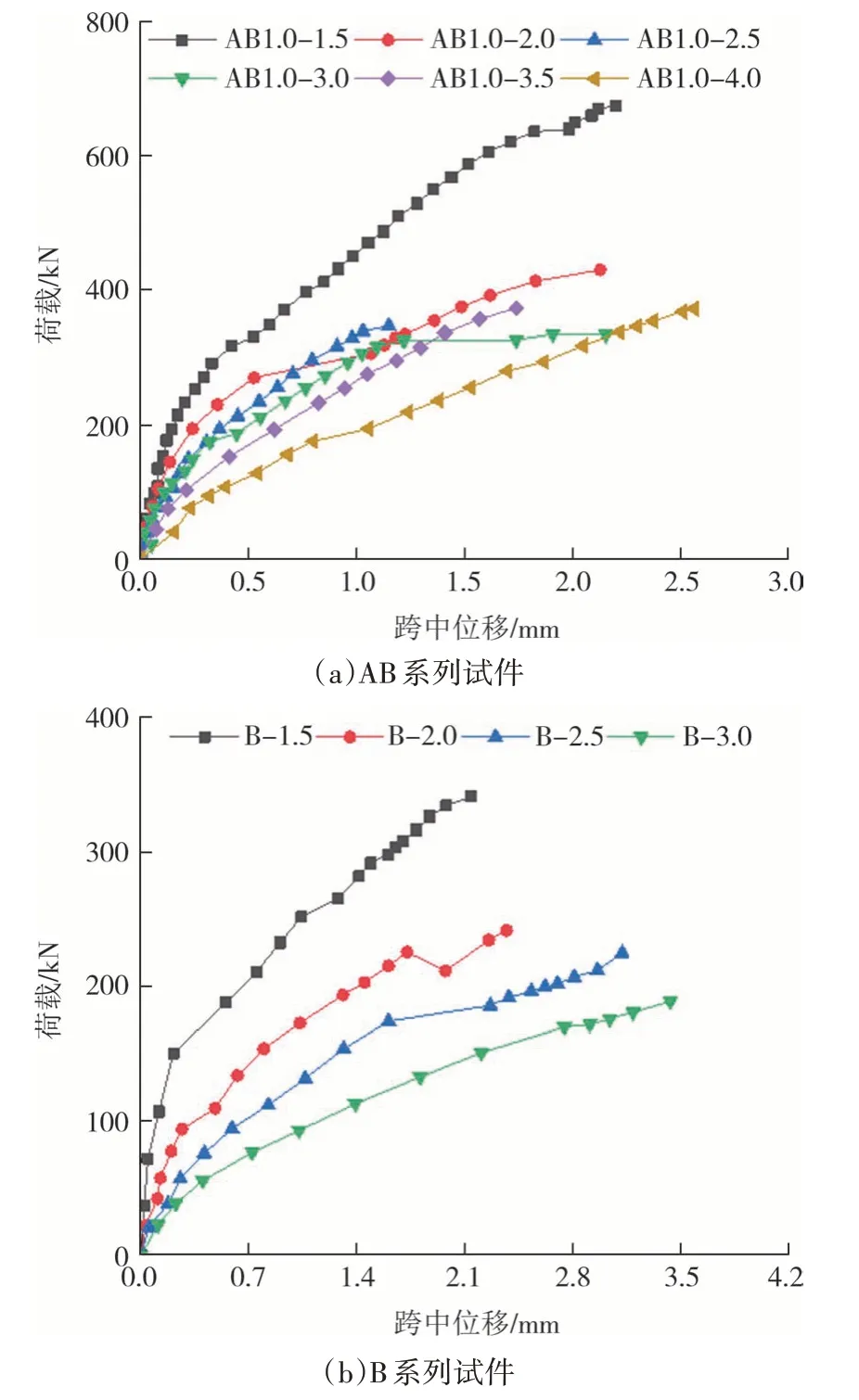
图6 荷载-跨中位移曲线Fig.6 Load-midspan displacement curves

试件AB1.0-1.5、AB1.0-2.0、AB1.0-2.5和AB1.0-3.0中大剪跨比分别与试件B-1.5、B-2.0、B-2.5和B-3.0 的剪跨比相同.其中，试件AB1.0-1.5 和AB1.0-2.0 中大剪跨段承担的剪力分别比B-1.5 和B-2.0 提高了58.0%、14.2%，而试件AB1.0-2.5 和AB1.0-3.0大剪跨段承担的剪力分别比B-2.5 和B-3.0 降低了12.0%、11.5%.上述现象，在一定程度上反映出非对称荷载作用下钢筋混凝土无腹筋梁受剪机理的复杂性，小剪跨段对大剪跨段的受剪承载力产生了显著影响.

2.4 纵筋应变分析

所有试件发生剪切破坏时，加载点正下方的纵向受拉钢筋均未屈服.其中，AB 系列试件中纵向受拉钢筋部分应变随荷载变化的情况如图7所示.

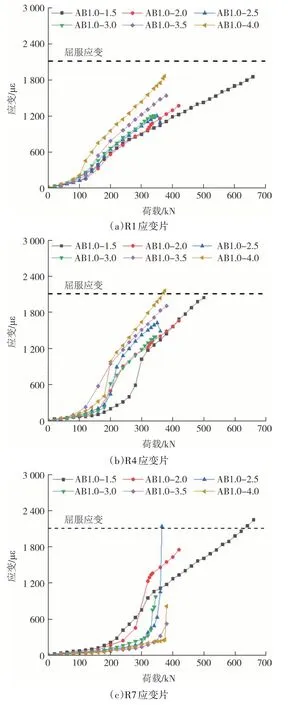
图7 纵筋应变-荷载关系曲线（AB系列）Fig.7 Strain-load relationship curves of longitudinal tensile reinforcement in AB series specimens

从图7（a）可以看出，AB 系列试件中加载点正下方纵向受拉钢筋在加载初期的应变值较小且基本相同；当达到极限荷载的30%左右时，由于该部位产生了竖向弯曲裂缝，钢筋应变开始出现不同程度的变化.图7（b）和图7（c）表明应变片R4 处的应变先于R7 出现剧增现象，这与前者所在截面的弯矩大于后者有关.

3 计算模型误差分析

假设非对称集中荷载在钢筋混凝土无腹筋梁中大、小剪跨段产生的剪力分别为VW和VE，而两剪跨段的实际受剪承载力分别为RW和RE.其中，VW和VE的大小与剪跨段长度成反比.理论上，当满足式（1）时，大剪跨段先发生剪切破坏；当满足式（2）时，小剪跨段先发生剪切破坏.

Kani［2］开展了大量钢筋混凝土无腹筋简支梁四点弯曲试验，不同配筋率的4 个系列试件试验结果如图8 所示.其中，所有试件的截面尺寸及有效高度均相同，混凝土圆柱体抗压强度约为 26.2 MPa.图8 中抗剪强度νu为梁受剪承载力试验值与截面宽度和有效高度之积的比值；λ为剪跨比；ρ为纵向受拉钢筋配筋率；混凝土轴心抗拉强度ft，m=0.88 ×并取从图8 可以看出，相同条件下不同纵筋配筋率的无腹筋梁具有不同的抗剪强度，抗剪强度随剪跨比的增大而呈非线性变化趋势，并均在剪跨比为2.5处出现了明显拐点.

图8 抗剪强度随剪跨比的变化Fig.8 Variation of shear strength with shear span-depth ratio

一方面，采用GB 50010—2010公式预测文献［2］中试件的受剪承载力，结果如图8 中虚线所示.计算过程中，剪跨比的取值范围为1.5～3.0.图8 表明GB 50010—2010公式预测无腹筋梁受剪承载力的精度较差，这与钢筋混凝土梁斜截面剪切破坏机理复杂且规范公式主要依据试验结果取下包络线有关.另一方面，采用GB 50010—2010 公式预测本文试件两剪跨段的受剪承载力和，并将其替代式（1）和式（2）中的RW和RE以判断剪切破坏位置，考虑试件AB1.0-1.5破坏模式的复杂性而不予讨论，结果见表2.从表2 可知，GB 50010—2010 公式预测得到梁发生剪切破坏的位置均与试验结果相反.

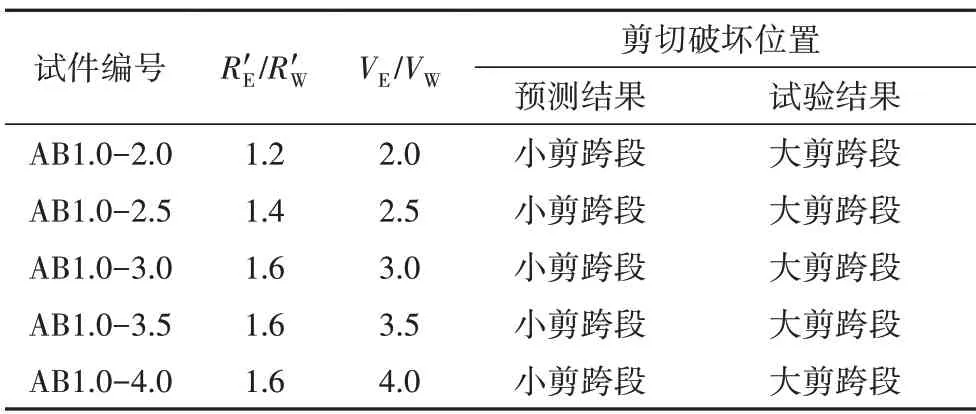
表2 剪切破坏位置Tab.2 The location of the shear failure

MCFT 公式、Choi 公式和Zsutty 统计公式的计算表达式，见表3.采用上述计算模型分别预测AB 系列试件极限承载力及剪切破坏位置，结果见表4.其中，剪切破坏位置判断的原则与表2 相同.考虑到同一试件中两剪跨段的剪跨比不同而不可能同时发生剪切破坏，以致不能简单地将两剪跨段受剪承载力的预测值直接叠加而得到梁的极限承载力.因此，本文分别利用两剪跨段的受剪承载力预测值推算梁所能承受的荷载Pcal，E、Pcal，W，并取Pcal，E和Pcal，W两者中的较小值作为极限承载力代表值Pcal.计算过程中，根据混凝土立方体抗压强度实测值平均值换算得到圆柱体抗压强度=34.2 MPa.计算截面按以下原则选取：MCFT 公式取与支座距离为（a-d）和0.5a中的较大值［20］；Choi公式和Zsutty统计公式取支座处截面.

表3 计算模型表达式Tab.3 Expressions of calculation models

表4 计算模型预测结果Tab.4 Prediction results of calculation models

从表4 可以看出，极限承载力试验值Pu与MCFT公式预测结果之比的均值为2.49，而且剪切破坏位置的预测结果均与试验结果相反.Choi 公式和Zsutty统计公式预测得到的Pu/Pcal均值分别为1.09和1.01，且两者预测剪切破坏位置的效果也较理想.相比之下，Zsutty统计公式的预测效果最好.