黄土盾构下穿不同地下非连续管线的模型试验
2024-03-31苏永华李明
苏永华 ,李明
(湖南大学 土木工程学院,湖南 长沙 410082)
地下交通作为城市主要的交通方式之一,建设穿越人口密集的繁华地带,盾构开挖掘进往往不可避免地穿越大量城市地下管线,引起地下管线发生沉降变形.施工中若无法有效控制管线的沉降变形,轻则影响地下管线的正常使用,重则造成区域性地表塌陷,危害附近居民的生命财产安全,因此研究不同地下管线在隧道施工扰动下的沉降受力规律尤为重要.
现有盾构隧道施工下穿管线的研究方法中,理论分析法[1-5]和数值模拟法[6-9]已经作为常用的研究方法.其中俞剑等[1]和魏纲等[2]均将管土作用看作Winkler 地基上的弹簧模型,将地下管线视作连续均匀介质,分析了盾构开挖对连续管线沉降计算方法.Huang等[4]则在前两位研究的基础上,以现场监测和离心实验为基础,为更贴合实际工程,将地下管线视为不连续的介质,提出了一种改进的Winkler 模量的Winkler 解析解来分析隧道直线开挖对地下非连续管线的响应问题.邓皇适等[5]则进一步补充了隧道在曲线开挖段对地下管线的影响,将管线看作放在Pasternak 地基上的欧拉伯努利梁,通过理论解,计算推导出盾构在曲线段引起的管线沉降公式.为重点研究管土相对刚度对管线沉降的影响,赵智涛等[6]利用有限元软件,构建结构、地层和管线三者相互作用的数值模型,分析不同管线刚度对地层沉降抑制的影响,提出了管土相对刚度的经验公式.
隧道开挖在管线变形受力研究分析过程中,模型试验法[10-23]也成了诸多学者重要的研究手段.朱叶艇等[10]和黄晓康等[11]采用量纲分析法以黏土为土体材料,将地下管线用PVC-U 连续管线代替,进而研究隧道在正交、斜交和平行下的连续管线变形情况.王海涛等[12]同样将地下管线视为连续管线,基于砂土地层的隧道施工探讨管、隧道埋深和管隧交角等因素对管线变形系数的影响,并提出安全控制标准,补充了在砂土地层下不同因素对管线变形的影响.由于前人研究均为圆形盾构下的连续管线,魏纲等[13]的模型试验首次采用管节与管段搭接方式模拟非连续管线,探讨了不同埋深下,类矩形盾构隧道施工对地下非连续管线和非连续破损管线的变形受力规律.在同时期,史江伟等[22]对圆形盾构下穿连续和非连续管线进行离心试验,得出非连续管线沉降与连续管线沉降差异较大,揭示管线非连续性被忽略是极为不安全的.现有研究已经将地下管线由连续管线转变为非连续管线,但对非连续管线研究的深度不够,对非连续管线的接头刚度和接头间距等鲜有研究,因此进行相关模型试验尤为重要.
故本文采用室内模型试验,模拟圆形盾构施工对地下管线及周围土体的影响,分析非连续管线的沉降、弯矩以及管土接触应力,讨论不同接头间距、不同接头刚度及不同管隧间距对非连续管线变形的影响.
1 室内模型试验设计
1.1 工程及试验概况
本次室内模型依托河南省连霍呼北联络线公路某区间盾构隧道施工,该工程地表深度20 m 以下均为黄土地层,盾构隧道施工时下穿自西向东输气管道,该管道直径为1.2 m,厚度为30 mm,采用X70 钢材焊接连接管段而成,在该区间,管道埋深地下3 m,并在管道底部正下方3 m 处进行盾构隧道开挖.根据工程概况并考虑到盾构隧道施工的大致扰动范围以及模型试验的边界效应问题,选取工程中隧道两侧4 倍的直径和隧道下部3 倍直径为实际隧道工程开挖尺度[10]进行试验.本次模型试验考虑的主要物理量:1)土体参数的指标:含水率ω、压缩模量Es、内聚力C、内摩擦角φ、土体重度γ;2)管线参数:管线直径D、管壁厚度T、管线刚度EPIP;3)盾构掘进参数:盾构直径d、盾构支护管片厚度t;4)因变量:管线的竖向沉降变形δ、弯曲应变ε.由于试验材料和装置限制,并考虑到隧道施工实际扰动范围[10],确定试验几何相似比为1/45,土体重度相似比为1,根据量纲均衡性原则和白金汉定理推出其他相似比:Cω=Cφ=Cγ=1;CC=CEs=CD=Cd=Ct=Cδ=45;CEpIp=455.
1.2 试验装置与材料
1.2.1 模型箱和盾构开挖装置
隧道施工试验模型箱如图1 所示,为了便于观察试验土体沉降及管线布设情况,模型箱四周侧壁采用厚度为2 mm 的有机玻璃,箱体底部采用1 mm厚度的钢板与箱体外框架焊接而成,形成整体.模型箱外框架采用角钢焊接而成,以保证在抽取套管的过程中模型箱整体有较强的抗弯能力,有机玻璃和角钢通过螺栓连接固定在一起.模型箱整体尺寸为1 300 mm×800 mm×800 mm,在模型箱底部上方450 mm 处预留圆形孔洞,孔洞尺寸略大于盾构模型外径.采用不同外径的304 不锈钢管作为盾构隧道开挖装置,其中外径D为140 mm、厚度为1 mm 的钢管作为盾构支护外壳,外径为137 mm、厚度为2 mm的钢管作为盾构隧道衬砌.
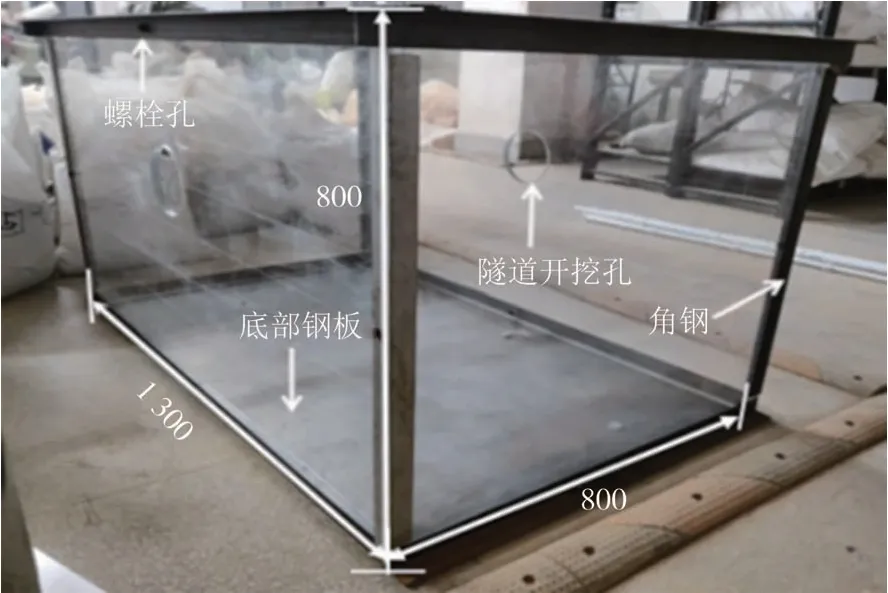
图1 模型装置示意图(单位:mm)Fig.1 Schematic diagram of the model device(unit:mm)
1.2.2 地下管线装置
对于地下管线的模拟,在不考虑管线自身重量的基础上,为满足所选的管道与实际工程管线在尺寸和刚度上具有相似性,经过比选采用PVC-U 管材模拟实际钢管.通过简支梁法对PVC-U 各型号管材的刚度进行计算,得出的模型管材参数与目标值差距极小.本模型试验分别以三种不同接头间距(非连续管线上两两相邻接头中点的水平距离)的非连续管线为研究对象,并且上述非连续管线接头分别采用刚度较大的硬质PVC 管段接头和刚度较小的LDPE(低密度聚乙烯)管段接头进行比较,非连续管线力学参数如表1 所示,管线接头长度(纵向轴线长度)均为30 mm,如图2所示.
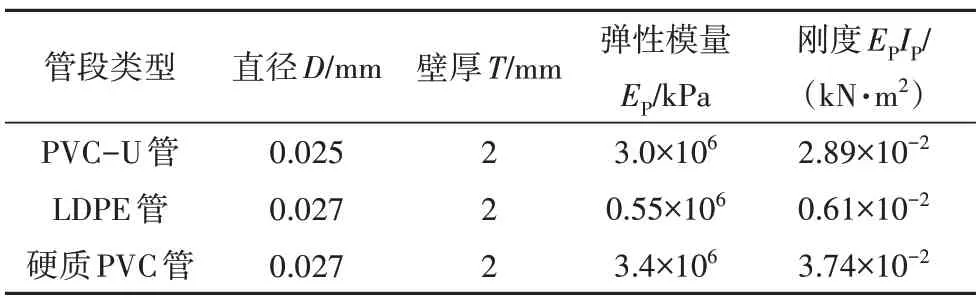
表1 非连续管线力学参数Tab.1 Mechanical parameters of discontinuous pipelines

图2 非连续管线示意图(单位:mm)Fig.2 Schematic diagram of discontinuous pipeline(unit:mm)
1.2.3 试验测量装置
试验主要测量的参数为管线沉降、管土接触应力、管线弯曲应变.管线沉降采用电子百分表和机械百分表(可精确至0.01 mm),通过架设磁力表座分别放置在管线沉降杆测量装置上;管土接触压力在管道轴线正下方等距埋设土压力盒(精度至0.01 kPa,0.5% FS),通过土压力的变化值来反映;管线弯曲应变是在管线底部轴线外表面处粘贴电阻应变片(灵敏度系数为2.01,片阻为120 Ω,测量精确至0.5 με)并接入至应变仪中,在电脑上获取应变数据,最后通过应变计算管段相应位置的弯矩.
1.2.4 试验配土材料
模型试验土体材料为连霍呼北联络线公路区间的工程黄土,经现场取土将土体进行人工筛选(筛分粒径<1 mm),再统一烘干调配含水率,通过环刀制样进行土力学基本物理特性试验,土体基本参数如表2所示.

表2 土体基本参数Tab.2 Basic soil parameters
1.3 试验内容与试验方案
1.3.1 试验内容
将土体材料每40 kg填至模型箱中,每填筑100 mm的高度夯实一次,夯实之后对黄土浅层表面进行凿毛处理,重复上述步骤至隧道埋深位置处,铺设双层不锈钢套管模拟盾构隧道装置,继续填土至地下管线埋深位置处将土压力盒平放压入土体内,再将提前粘贴好应变片的管线放置在土压力盒之上,将管线沉降测量杆环箍在管线上,继续覆土至试验设计高度处(750 mm),在管线沉降测量杆上安装电子百分表和机械百分表,并将各个导线按编号接入至应变仪通过采集系统实时获取数据.在采集系统正常使用情况下,利用电动拉拔器械,缓慢匀速抽出外层不锈钢管20 次,每次以10 mm/min 的速度进行抽取,在每次套管抽出40 mm 后(模拟实际盾构每环掘进1.5 m),停止10 min,再进行下一步开挖,直至外层套管被抽出,来模拟盾构20步隧道开挖.
1.3.2 试验方案
黄土地层盾构开挖引起地下管线变形根据管线接头间距和接头刚度共分为7组工况.定义Rr=EP1IP1/EP0IP0(非连续管线接头与管段相对刚度比),表示不同接头刚度下的非连续管线;定义L=Li/Lj为归一化非连续管线接头间距(Li为接头间距、Lj为管线总长),如表3所示.其中工况7为连续管线下的试验工况作为对照组,以连续管线的试验数据为基准进行分析对比.连续管线和非连续管线均在管隧正交、管线埋深70 mm,管隧间距70 mm 相同的条件下进行模型试验.模型箱中的试验测点分布示意图,如图3 所示.其中,G1~G5为机械和电子百分表位移计测量的管线垂直沉降位移,百分表间距不相等,从中间至两侧的间距分别为90 mm、90 mm、108 mm 和180 mm;Y1~Y11为电阻应变片测量管线弯曲应变与内力,应变片间距均为130 mm;T1~T7为应变式微型土压力盒传感器测量管线表面与土体之间的接触应力(埋设位置位于管线底部轴线20 mm 位置处),土压力盒等间距分布间距均为162.5 mm.

表3 模型试验工况设计Tab.3 Model test condition design
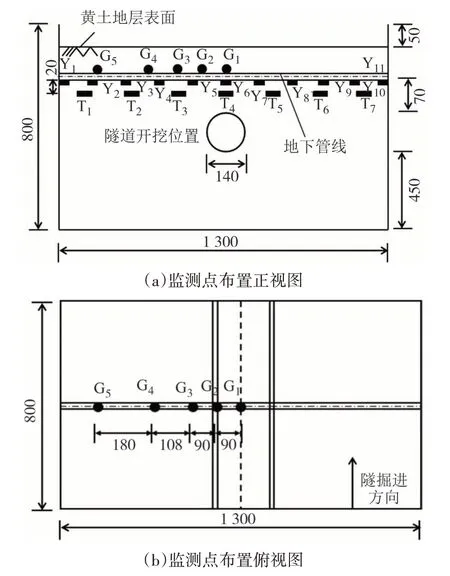
图3 模型试验监测点布置示意图(单位:mm)Fig.3 Schematic layout of monitoring points for the model test(unit:mm)
2 试验结果分析
2.1 接头间距对不同非连续管线沉降研究
2.1.1 PVC接头非连续管线
图4 为PVC 接头非连续管线(Rr=1.30)在不同接头间距下管线沉降最终曲线.由图可知,当Rr=1.30 时,非连续管线的最大沉降Smax随着接头间距L减小(接头数量的增加)逐渐减小.管线最大沉降值发生在隧道中轴线位置处.隧道开挖引起管线主要沉降(沉降≥10%Smax)的横向影响范围在-2.1D~2.1D,管线沉降随着远离隧道中轴线而逐渐减小直至趋近于0.当接头间距L为0.50、0.33、0.25 时,非连续管线最大沉降分别为0.32%D(0.45 mm)、0.3%D(0.43 mm)、0.26%D(0.36 mm),管线沉降由于接头间距的减小,沉降主要差异区(相同测点沉降差>0.05 mm)介于距离隧道中轴线-1.3D~1.3D.上述数据说明,当Rr=1.30,接头间距由0.5减小至0.25时,非连续管线的最大沉降呈折线型减小,接头间距对非连续管线沉降的横向影响范围占管线主要沉降的62%,在该范围外,接头间距对管线沉降几乎无影响.
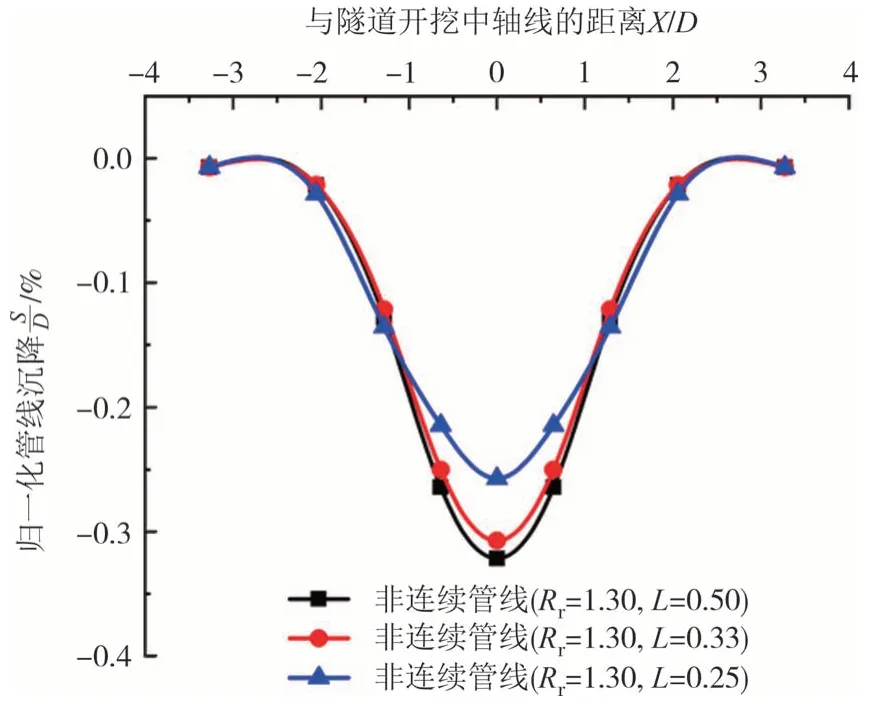
图4 不同PVC接头间距下非连续管线最终沉降曲线Fig.4 Final settlement curve for discontinuous pipelines with different PVC joint spacing
图5 为G1测点下在距离隧道掌子面(Y/D)的归一化距离处,非连续管线纵向沉降的变化.隧道掌子面在通过测点前-1.43D,管线沉降随着掌子面推进距离的增加而缓慢增大;隧道掌子面在距离-1.43D~1.43D处,管线沉降随掌子面推进骤然增大;掌子面在通过测点1.43D后,管线沉降增幅减小.当Rr=1.30时,隧道掌子面位于-1.43D~1.43D范围内,管线沉降占管线沉降总值的85%,定义该范围为非连续管线的沉降集中区.在该沉降集中区内,随着L的减小,非连续管线的平均沉降增长速率(归一化管线沉降/距离)为0.065、0.060、0.055.这说明,当Rr=1.30,接头间距L为0.5~0.25 时,随着L减小,管线沉降平均增长速率呈线性减小,管线沉降历时曲线形态变化明显.产生该现象是由盾构掌子面距离和地下管线整体刚度共同决定的,随着接头间距减小,接头数量增大,管线抵抗变形能力大,在相同掌子面开挖距离下,沉降变形的滞后性更大.
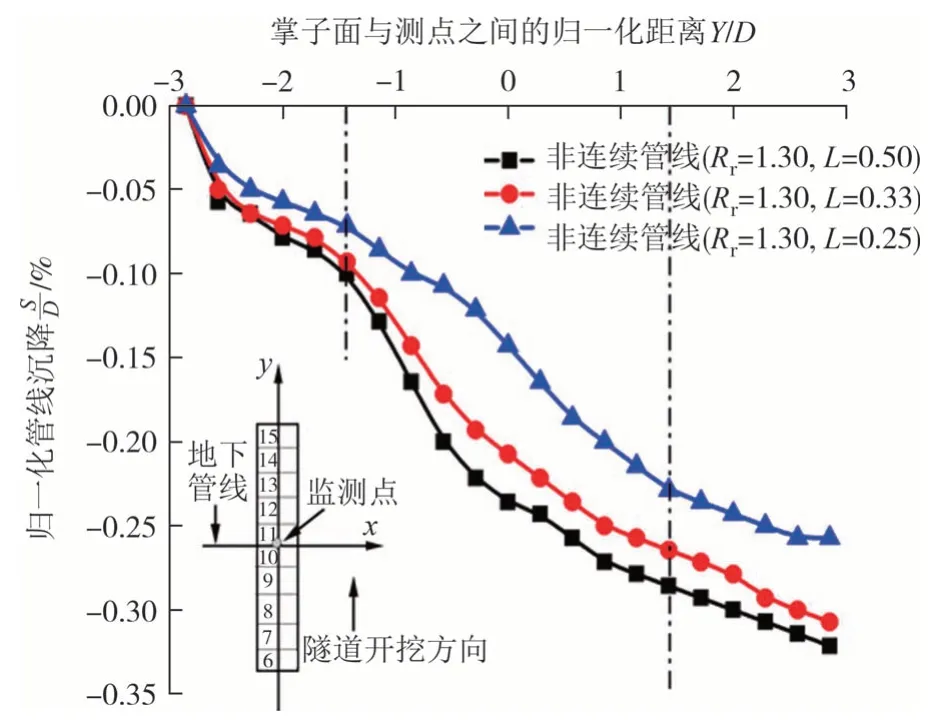
图5 G1测点下PVC接头非连续管线沉降历时曲线Fig.5 Settlement ephemeris curve for non-continuous pipeline with PVC joints under measurement point G1
2.1.2 LDPE接头非连续管线
图6 为LDPE 接头非连续管线在不同接头间距下管线沉降最终曲线,观察图6 可知,当Rr=0.21 时,非连续管线的最大沉降随着接头间距L减小逐渐增大,隧道开挖引起管线主要沉降的横向影响范围在-2.1D~2.1D.当接头间距L为0.50、0.33、0.25时,非连续管线最大沉降分别为0.37%D(0.52 mm)、0.39%D(0.55 mm)、0.44%D(0.61 mm).以上数据说明,当Rr=0.21,接头间距由0.5 减小至0.25 时,非连续管线的最大沉降呈折线型增大.此外,通过对比图4 和图6可知,当非连续管线接头与管段相对刚度比由1.30减小至0.21 时,非连续沉降主要范围和沉降主要差异区均无变化,这说明,管线整体刚度对管线沉降范围几乎无影响.故在实际控制管线沉降范围区时,应通过调整隧道开挖半径等其他方式进行控制.

图6 不同LDPE接头间距下非连续管线最终沉降曲线Fig.6 Final settlement curve for discontinuous pipelines with different LDPE joint spacing
图7 为G1测点下不同LDPE 接头间距下非连续管线归一化沉降历时曲线.由图可知,LDPE 接头非连续管线的沉降集中区同样在-1.43D~1.43D的范围内.在该范围内管线沉降增幅最大,L为0.5、0.33、0.25下的非连续管线的沉降分别由0.11%D、0.13%D、0.14%D增大至0.34%D、0.36%D、0.38%D,管线的平均沉降增长速率均为0.08左右.在Rr=0.21,接头间距L在0.5~0.25 之间时,随着L减小,管线沉降平均增长速率基本不变.分析原因可能是LDPE接头非连续管线接头刚度较小,使得管线整体刚度弱化,管线抵抗土体变形能力较小,此时盾构开挖掌子面与管线距离成为影响管线沉降速率主要原因,由于盾构推进速度不变,导致管线沉降速率基本不变.通过对比图7 和图5 可知,Rr的大小对非连续管线沉降集中区范围影响不大,对沉降集中区管线平均沉降增长速率影响较大.Rr由1.30 减小至0.21 时,管线平均沉降增长速率增大1.5倍.

图7 G1测点下LDPE接头非连续管线沉降历时曲线Fig.7 Settlement ephemeris curve for non-continuous pipeline with LDPE joints under measurement point G1
2.2 接头间距对不同非连续管线弯矩研究
2.2.1 PVC接头非连续管线
图8 为Rr=1.30 时,不同L下的非连续管线在盾构开挖结束后最终弯矩曲线,在参考Klar[3]研究的基础上将结果进行归一化:①弯矩Mi2/EISmax;②与隧道开挖中轴线的距离X/D,图中弯矩负值表示管线受拉.由图可知,在Rr=1.30 的非连续管线的弯矩,随着接头间距L的减小,非连续管线的最大正负弯矩均在增大,最大正弯矩发生位置由距离隧道开挖中轴线X/D为0 处转移至0.7D处,最大负弯矩发生位置在1.9D处基本不变.在Rr=1.30 下,非连续管线的接头间距L由0.5 减小至0.25 时,对非连续管线弯矩曲线和最大负弯矩值影响显著,最大负弯矩增幅为138%,弯矩整体呈现出上“M”下“W”形.分析原因大致为采用较大刚度的PVC 作为非连续接头,接头处存在环箍作用,使得非连续管线的变形受力不连续,管线内力随着接头间距减小,受力集中,没有体现出管线柔韧性.
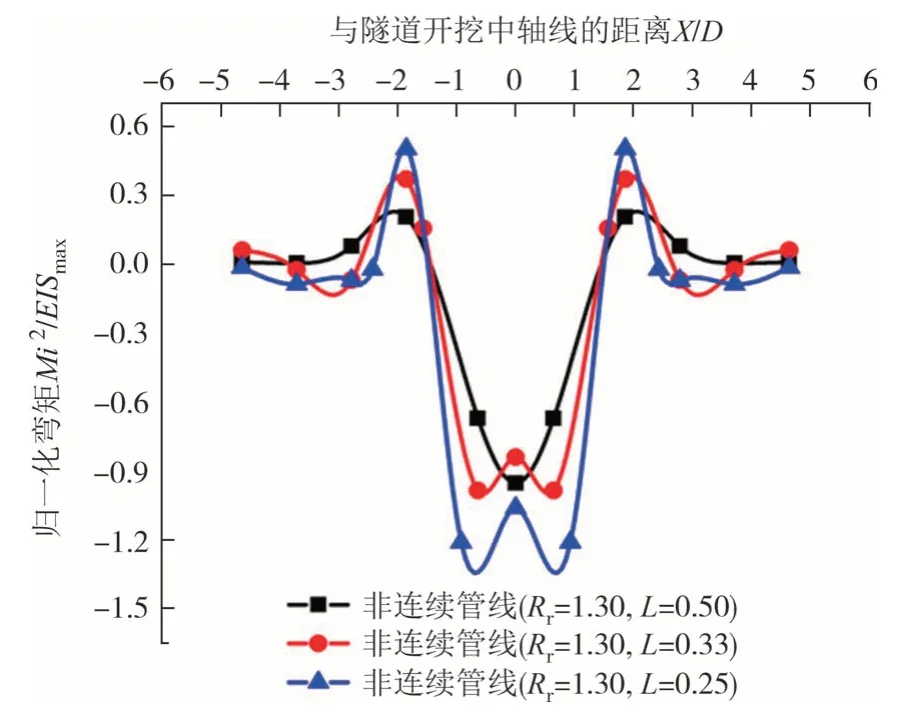
图8 不同PVC接头间距下的非连续管线弯矩曲线Fig.8 Bending moment curves for discontinuous pipelines with different PVC joint spacing
2.2.2 LDPE接头非连续管线
图9 为Rr=0.21 时,不同L下的非连续管线在盾构开挖结束后弯矩曲线,对结果同样采用归一化处理.由图可知,在Rr=0.21 的非连续管线的弯矩,随着接头间距L的减小,非连续管线的最大正负弯矩均在增大,最大正弯矩发生位置在距离隧道开挖中轴线X/D为0 处,最大负弯矩发生位置在1.9D处.当L=0.50 时,最大正负弯矩值为0.87 和-0.36;当L=0.33时,最大正负弯矩值为1.85 和-0.64;当L=0.25 时,最大正负弯矩值为2.55和-0.76.通过数据分析发现,在Rr=0.21 下,非连续管线的接头间距L由0.5 减小至0.25 时,接头间距仅改变非连续管线最大正负弯矩值,对管线弯矩分布形态无影响,最大正弯矩增幅为193%,最大负弯矩增幅为111%.

图9 不同LDPE接头间距下的非连续管线弯矩曲线Fig.9 Bending moment curves for discontinuous pipelines with different LDPE joint spacing
2.3 不同接头刚度对非连续管线沉降研究
为明确不同L下的不同Rr的非连续管线沉降与弯矩差异变化规律,以连续管线为对照组,进行对比分析.图10 为三种接头间距L下不同Rr的非连续管线与连续管线的沉降对比曲线,由图可知,当L为0.50、0.33 和0.25 时,不同Rr的非连续管线的最大沉降值与连续管线沉降值差异越来越大,其中Rr=1.30的非连续管线最大沉降比连续管线减小0.04%、0.05%和0.1%;Rr=0.21 的非连续管线最大沉降相比连续管线增大0.01%、0.03%和0.08%.管线沉降差异区并不随L和Rr的改变而改变,连续管线和非连续管线沉降差异均发生在-1.3D~1.3D.上述结果说明,Rr的大小对非连续管线的沉降值具有决定性作用(决定管线最大沉降的上限和下限),两种不同Rr下的非连续管线沉降最大差值可达0.18%D.在盾构下穿管线施工控制管线沉降中,对于不同接头间距下的不同管线都应该在-1.3D~1.3D范围内加强施工安全控制.
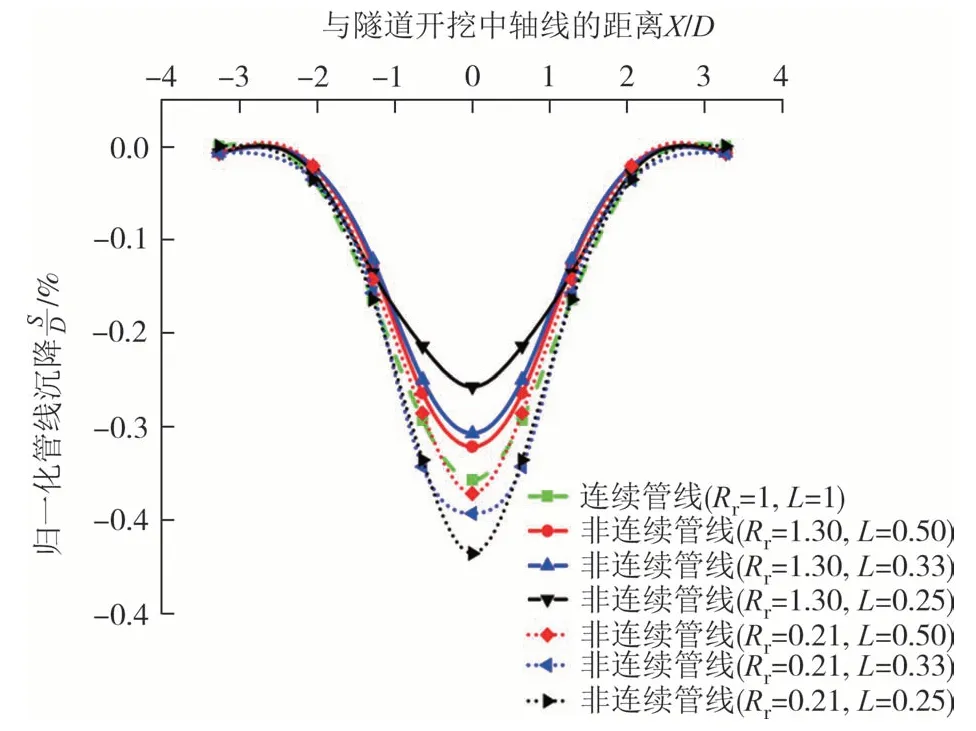
图10 连续和非连续管线的沉降对比曲线Fig.10 Settlement comparison curves for continuous and discontinuous pipelines
考虑接头间距、接头刚度和管线刚度三者综合影响下对非连续管线最大沉降的影响,提出非连续管线综合刚度比RL,用来描述非连续管线整体相对刚度大小,RL越小表示非连续管线整体刚度越小,RL计算公式如式(1)所示.其中(EPIP)i和(EPIP)j分别为接头刚度和管段刚度,T1、T2和T0分别为接头总长、管段总长和非连续管线总长.
图11 给出不同RL下非连续管线最大沉降变化规律,可见非连续管线整体刚度大小和管线最大沉降(Smax0)能较好服从3 次多项式拟合函数,如式(2)所示.从图11 可以看出,随着RL的增大,管线最大沉降呈阶梯式增大,增幅先增大后减小再增大;当RL减小至1 时,管线最大沉降值陷入拐点,在RL小于1 时管线最大沉降增幅变大,故在非连续管线RL小于1时管线可能产生较大沉降变形,在施工过程中应尽力避免或做好控制措施.
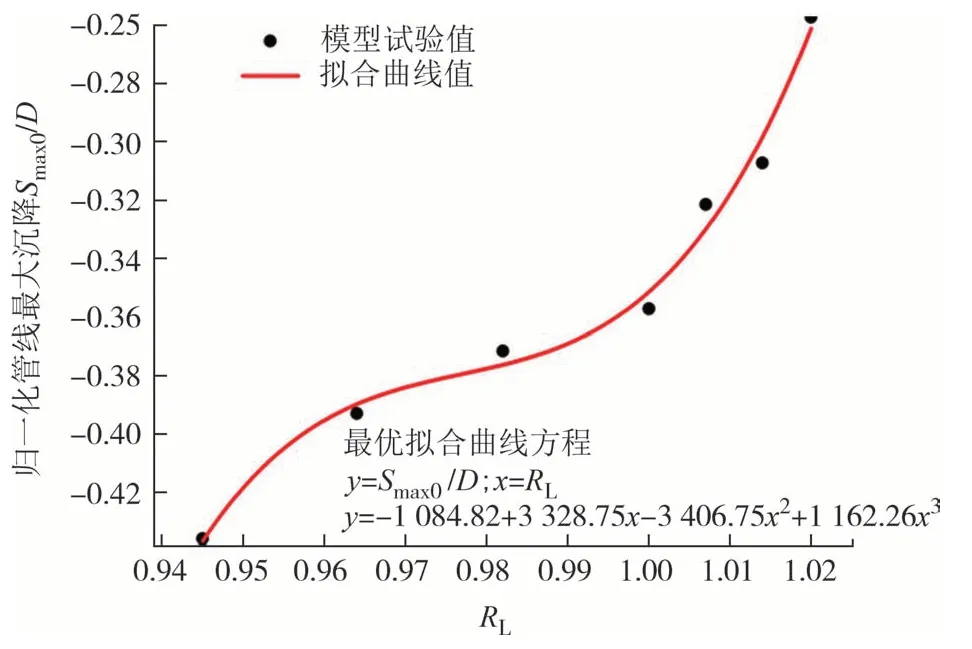
图11 不同RL下的管线最大沉降Fig.11 Maximum settlement of pipelines at different RL
2.4 不同接头刚度对非连续管线弯矩研究
图12 为三种接头间距L下不同Rr的非连续管线与连续管线的弯矩对比曲线,由图可知,不同Rr下的非连续管线,随着L由0.50 减小至0.25,管线最大正负弯矩值均增大,Rr=0.21 下的非连续管线弯矩值始终大于Rr=1.30 的非连续管线,但小于连续管线弯矩值.当接头间距L相同时,随着L的减小,不同Rr下非连续管线最大正弯矩增幅由-10%、90%增大至95%,最大负弯矩增幅基本维持在70%,由数据推测出,地下管线最大正弯矩与最大负弯矩可能存在一定关系.不同Rr非连续管线弯矩始终小于连续管线弯矩,这是由于管线接头处存在与管段相互作用,导致非连续管线的受力不连续,管线接头处不仅存在抗弯受拉,在管节接头与管段之间还存在扭转与转角问题,三者共同作用下极大减小了管线所受弯矩.而连续管线不存在管节接头,受力连续均匀,无法通过扭转和发生相对转角而减小所受的弯矩值.
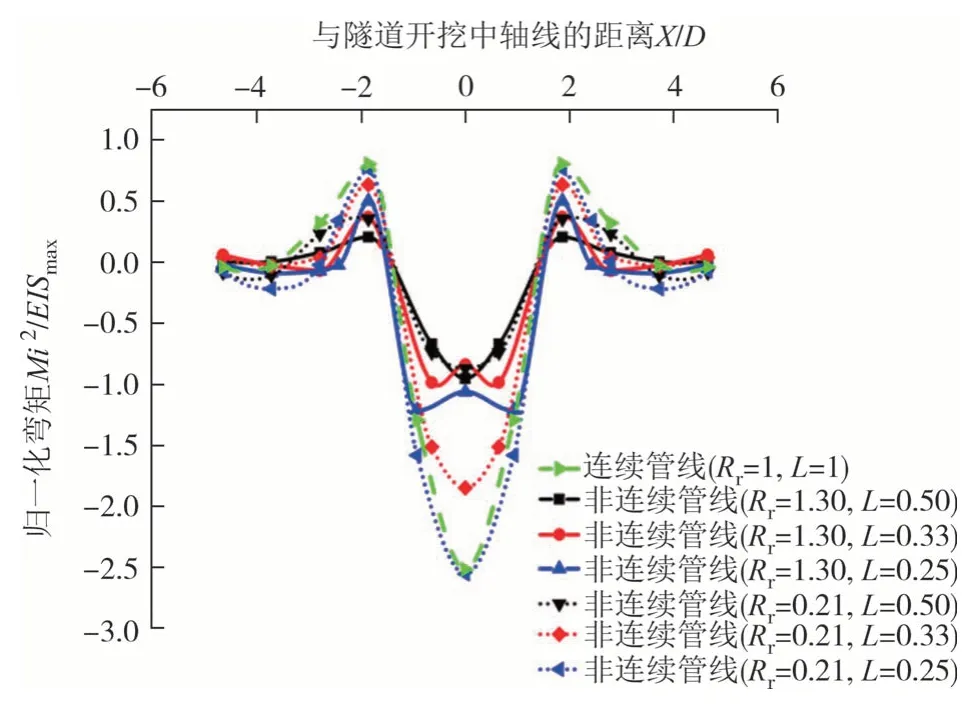
图12 连续和非连续管线的弯矩对比曲线Fig.12 Bending moment comparison curves for continuous and discontinuous pipelines
为研究不同L下不同Rr的管线最大正负弯矩相对变化规律,采用不同综合刚度比RL下的管线最大正负弯矩(M1和M2)值进行一一对应,通过拟合得出两者相对关系,如图13 所示.由图可知,不同RL下的管线最大正弯矩值与最大负弯矩值均呈现服从4 次多项式函数关系,如式(3)所示.当最大负弯矩小于0.4 时,随着负弯矩的增大,管线最大正弯矩基本不变;当最大负弯矩大于0.4 时,管线最大正弯矩随着最大负弯矩的增大呈一定比例的增加.所以当地下管线最大负弯矩大于0.4时,管线的受力进入最大正弯矩急剧增大拐点,在盾构施工过程中应该减小和控制管线受力.
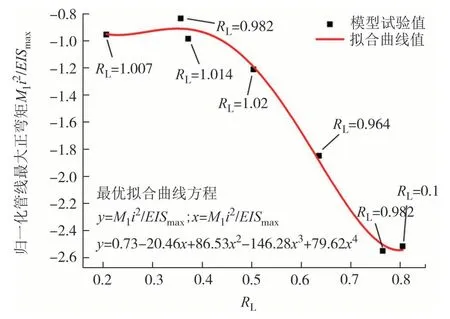
图13 不同RL下的最大正弯矩与最大负弯矩关系曲线Fig.13 Maximum positive bending moment versus maximum negative bending moment at different RL
2.5 管土接触应力变化规律研究
图14 为隧道开挖在7种工况下连续管线和非连续管线的管土接触应力变化(隧道开挖前后土压力比较)曲线.观察图14 可知,在L相同的工况下,Rr=1.30 的非连续管线的正负峰值土压力始终大于Rr=0.21 的非连续管线;在相同Rr下,L的增加会增大管土接触应力的峰值应力,其中Rr=0.21 的非连续管线由于存在刚度弱化节点,管土沉降变形更协调,管线负峰值土压力由负转正,管线整体接触应力均为正值.连续和非连续管线的管土接触应力变化均呈现“双峰型”变化,峰值应力随着L的增大而增大,接触应力负峰值在X/D为0 处,正峰值发生在±1.2D处,Rr和L的大小并未改变管土接触压力分布形态.盾构下穿管线施工中,需要在-1.2D~1.2D范围内加强对土压力变化的监测,根据正负峰值土压力判断管线变形情况.

图14 连续与非连续管土接触应力变化曲线Fig.14 Soil contact stress variation curves for continuous and discontinuous pipelines
2.6 不同管隧间距对管线沉降变形研究
为探究盾构开挖时,不同管隧间距、管线接头刚度、接头间距三者综合作用下,对管线沉降变化的影响规律,采用三维有限元软件建立管隧间距H在3 m、6 m、9 m下的工程足尺模型,重点分析了不同管隧间距下不同地下管线的最大沉降值变化规律,如图15所示.由图可知,在H一定时,管线最大沉降随着接头刚度的增大而减小,Rr=1.30 的非连续管线随着L的减小而减小,Rr=0.21的非连续管线随着L的减小而增大,该规律与上述模型试验管线沉降规律一致;管线最大沉降值随着管隧间距的增大出现近似折线型减小,沉降转折点出现在管隧间距与隧道开挖直径比H/D为1 处附近.即当H/D小于1 时,管隧间距对管线沉降变化影响极为显著,此时管隧间距对管线沉降影响占主导作用.故在实际工程中,为减小管隧间距带来的影响,应尽可能在H/D大于1下的深度处进行隧道施工.

图15 不同H下管线最大沉降变化曲线Fig.15 Variation curve of maximum settlement of pipeline under different H
3 结论
1)在沉降集中区,随着接头间距L由0.50 减小至0.25,Rr=1.30 的非连续管线最大沉降值呈折线型减小,沉降平均增长速率线性减小;Rr=0.21 的非连续管线最大沉降值呈折线型增大,沉降平均增长速率基本不变.Rr的大小对非连续管线对沉降集中区管线平均沉降增长速率影响较大,Rr由1.30 减小至0.21 时,非连续管线平均沉降增长速率最大增大1.5倍.Rr相对大小对非连续管线沉降和弯矩起到决定性作用,两种不同Rr下的非连续管线沉降最大差值可达0.18%D,最大正弯矩差值百分比为95%.
2)通过定义非连续管线综合刚度比RL,揭示了不同RL下非连续管线最大沉降变化规律和管线最大正负弯矩相对变化规律.其中,RL与管线最大沉降服从3次多项式拟合函数,在RL小于1时管线最大沉降增幅增大;管线的最大正弯矩值随着最大负弯矩值的改变服从4 次多项式拟合函数,当最大负弯矩大于0.4时,管线进入最大正弯矩急剧增大拐点.
3)连续和非连续管线的管土接触应力变化均呈现“双峰型”变化,管土接触峰值应力随着L的增大而增大,Rr和L的大小对管线的管土接触应力分布形态和分布范围无影响.
4)地下管线最大沉降随着管隧间距H增大而呈现折线型减小,该转折点出现在H/D为1 附近处.当H/D小于1 时,管隧间距对管线沉降影响占主导作用.
