考虑不同充电策略的锂电池健康状态区间估计

张孝远, 张金浩, 杨立新

(河南工业大学 电气工程学院,郑州 450001)

在碳达峰、碳中和目标背景下,电动汽车得到大力发展.锂离子电池作为电动汽车的核心部件之一,使用量呈现井喷式增长.与此同时,由锂离子电池健康状态(State of Health, SOH)劣化引发的安全问题日益凸显,在一定程度上限制了电动汽车行业的发展.SOH通过百分比的形式量化电池的老化情况,是评价电池老化程度的综合评价标准[1].合理精确的SOH估计有助掌握电池的衰减情况,对电池安全使用、维护管理和经济性评估都有十分重要的意义[2-3].

SOH无法通过传感器直接测量,现有SOH评估方法主要分为模型法和数据驱动法[4].模型法基于电化学机理建立物理等效电路模型来描述锂离子电池SOH的变化,模型参数可依据电池的不同衰退情况而变化,但锂电池内部化学变化是一个动态、非线性的复杂电化学系统,建立准确的电化学模型非常困难[5].相较之下,数据驱动法无需考虑电池内部复杂的电化学机理,仅基于大量充放电数据提取能够表征电池SOH的特征参数,即可建立特征参数与SOH之间的定量映射关系.因此,基于数据驱动的锂电池SOH估计得到众多研究者的青睐[6-7].

数据驱动法一般包含特征参数选取和SOH回归估计两大步骤.提取出能够充分表征SOH的特征参数是近年来的一个研究热点,文献[8]中从充放电曲线中获取增量容量(Incremental Capacity, IC)曲线,研究了IC曲线随循环次数的变化趋势,并验证IC峰值、IC峰值位置等特征与SOH之间的相关性,但不同型号电池的IC峰值数量并不一致,所用特征并不适用于所用电池.文献[9]中进一步研究不同型号电池包含多个IC峰值的情况.但在IC曲线的提取过程中必须设计复杂的滤波算法来平滑原始电压测量值,同时,IC峰值位置会随着电池老化而逐渐偏移;并且要获得所有老化周期下的IC特性,需要在较大的电压范围内进行采样,十分耗时.针对这个问题,文献[10]中从放电电压曲线及温度曲线中获取放电平均电压和平均温度作为外部特征,估算SOH.但在实际应用中,电池放电深度不一致导致平均电压变化且温度受环境影响较大.为此,文献[11]中选择从恒压充电曲线中获取平均电流等作为外部特征,并用等效电路模型表征恒压曲线中的电池老化现象.上述锂电池特征参数提取的最新研究较大程度上推动了基于数据驱动的锂电池SOH估计的发展.但上述研究有一个共性不足——都是基于恒流恒压充电策略下进行的锂电池充放电实验,所用数据均为单一充电策略下所得数据,未考虑不同充电策略或锂电池实际放电情况等问题,在实际应用中缺乏普适性.研究高效准确的适用不同充电策略的锂电池特征参数选择方法是迫切的现实需求.

获得与SOH高度相关的特征参数之后,需要建立所获取特征参数与SOH之间的映射关系,其本质是一类多元回归问题.诸多机器学习方法可以用于解决这类问题.反向传播(BP)神经网络、支持向量机、高斯回归、决策树等方法相继被用来建立SOH的回归估计模型[4].如文献[12]中搭建BP神经网络对锂电池SOH进行在线估计;文献[3]中采用粒子群优化的支持向量回归模型实时估计不同老化状态下的电池SOH;文献[13]中基于高斯过程回归(Gaussian Process Regression, GPR)建立SOH估算模型,取得较精确的估算精度;文献[10]中搭建布谷鸟搜索支持向量模型实现锂离子电池的SOH快速估计.结合前述特征参数选取方法,上述回归估计模型在特定条件下能够较为精确地估计SOH值,但上述研究所采用的SOH估计模型均为点估计方法.实际工作环境中锂电池剩余容量存在容量回升效应[14],随着循环次数的推移,锂电池剩余容量会有一定幅度的波动甚至上升,导致在某一时刻的SOH估计结果无法充分揭示SOH的退化趋势.同时,在实际运行中电动汽车工作环境复杂、负载波动较大,导致锂电池退化模式不固定,SOH估计结果具有一定的不确定性[15],传统点估计方法无法对锂电池退化过程进行合理量化.

针对锂电池SOH估计的不确定性量化估计问题,近年来有研究人员提出两类方法来构建电池SOH的预测区间.第一类为理论方法,基于以下假设:预测误差遵循具有零均值的确定分布,通常为正态分布或拉普拉斯分布[16].文献[17]中开发了一个基于平均熵和相关向量机的多步预测模型,并将其应用于电池的SOH评估和剩余寿命预测,该方法基于高斯分布构造95%的预测结果置信区间.但实测的锂电池充放电数据涉及复杂过程和噪声干扰,很难确保满足高斯假设.第二类为神经网络方法,该类方法无需考虑误差分布,因此受到研究者青睐.如文献[18]中构建了一个改进的上下边界估计神经网络对锂电池SOH进行区间估计.但此算法需要大量数据集进行训练,而锂电池全生命期,即SOH从100%退化到80%,一般循环次数不超过 2 000,属于典型的小样本问题,这类方法效果有限.

针对当前有关锂电池SOH估计方面的研究在特征参数选取普适性和SOH估计不确定性量化两方面的不足,提出一种适用于多种充电策略的锂电池SOH不确定量化估计方法.该方法充分考虑当前常用充电策略下充放电曲线的变化,从电压、电流及IC曲线中提取出多个外部特征,再通过交叉验证方法自动选取出适用于不同充电策略的个性化最优特征组合.首次提出使用支持向量分位数回归(Support Vector Quantile Regression, SVQR)模型进行锂电池SOH区间估计.所采用的SVQR方法利用分位数回归(Quantile Regression, QR)模型解决了区间分布问题,同时,支持向量回归(Support Vector Regression, SVR)模型在小样本充放电数据下具有较好的泛化性能.将所提方法在常用的3种不同充电策略的锂电池数据集上进行验证,并与QR、分位数回归神经网络(Quantile Regression Neural Network,QRNN)及GPR进行对比,验证了所提方法的优越性.

1 所提方法的总体框架

所提方法的总体流程如图1所示,分为离线训练和在线评估两个阶段.在离线训练阶段,首先从循环电压曲线、电流曲线及IC曲线中提取多个通用特征参数,然后采用交叉验证方法自动选择与SOH相关性最好的最优特征参数组合,并将其输入SVQR模型进行训练.在线阶段将充放电数据输入训练好的SVQR模型,实现电池SOH的在线区间估计,从而给出锂电池使用安全指导建议.

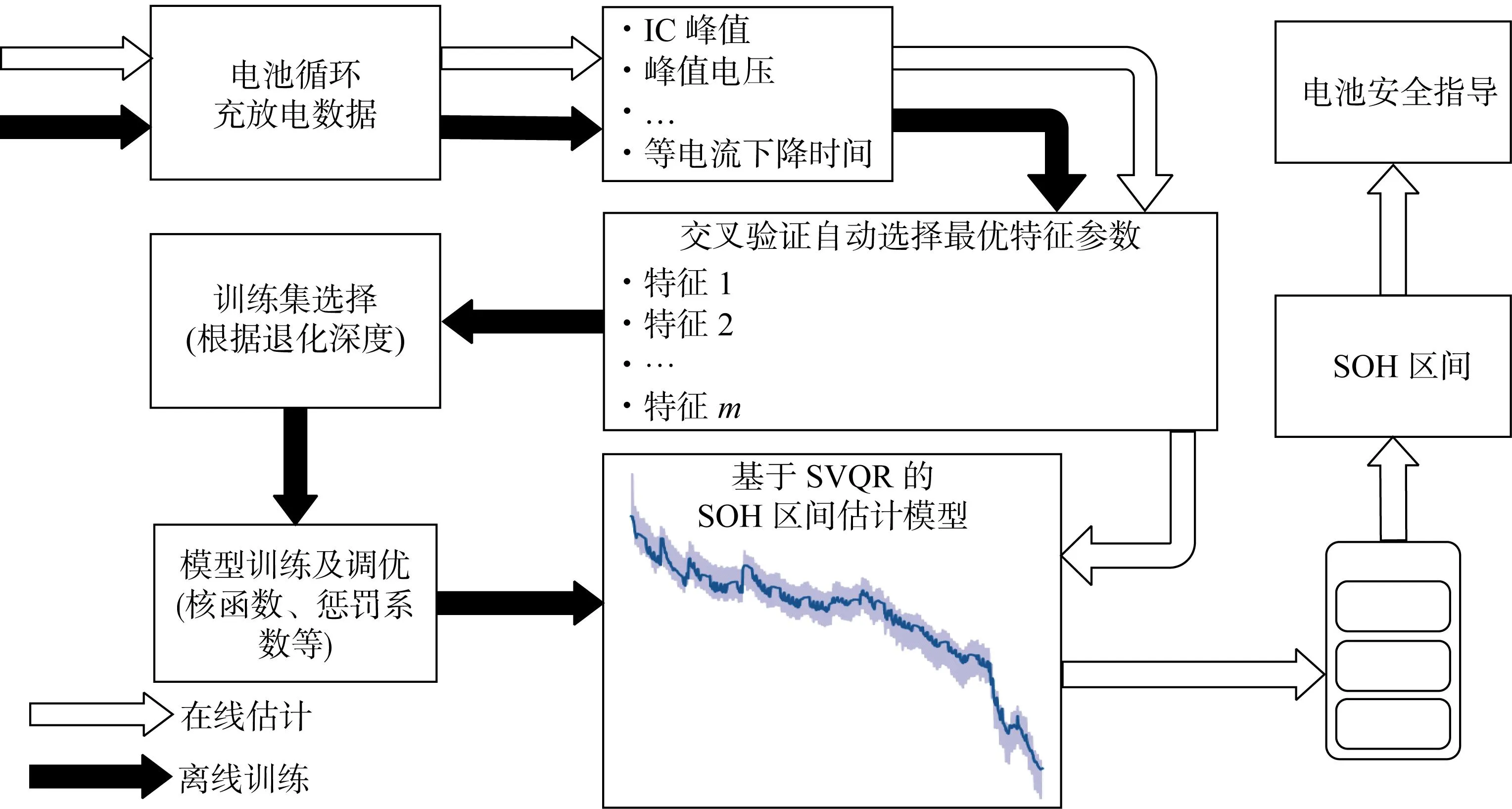
图1 所提SOH区间估计方法流程Fig.1 Flow chart of the proposed SOH interval estimation method

2 考虑不同充电策略的锂电池SOH 区间估计方法

2.1 锂电池常用充电策略及其特点

锂电池充电速度是制约电动汽车进一步发展的主要瓶颈之一[19].人们希望提高充电速度,但充电速度的提高会造成温度的快速升高和电池寿命的快速衰退.因此,探索能够兼顾充电快速性、温度控制与合理寿命预期的充电策略一直是一个研究热点[20].目前锂电池充电策略已由最初的恒压充电、恒流充电,发展到恒压恒流充电结合的多阶段充电[21].结合当前锂电池充电策略发展的现状,重点考虑如下3类常用的充电策略.第一类为恒流恒压(Constant Current Constant Voltage, CC-CV)充电.CC-CV充电第一阶段以恒定电流充电;当电压达到预定值时转入第二阶段进行恒压充电,此时电流逐渐减小;当充电电流下降到0时,蓄电池完全充满.该充电策略可有效避免电池极化效应,但充电时间较长;第二类为恒流(Constant Current, CC)充电.CC充电采用恒定电流对电池进行充电.由于电流一般较大,电池会快速达到截止电压,充电时间较短,但控制不得当则会增大电芯的极化;第三类为两阶段快速充电(Two Step Fast Charge, 2-step).该充电策略历经两个充电阶段.充电过程可表达为“C1(Q1)-C2”,其中C1和C2分别代表两个充电阶段,Q1代表充电电流切换时电池的荷电状态(State of Charge, SOC),第一个阶段采用恒流充电至SOC为Q1结束;第二个阶段采用CC-CV方式直至电池充满.上述3种充电策略的电压变化曲线如图2所示.

图2 不同充电策略下电压变化Fig.2 Voltage change of different charging strategies

2.2 SOH特征选择

锂电池充放电曲线中蕴含丰富的电池老化信息.图3为某单体电池不同循环次数下电压、电流变化曲线.可见,随着循环次数增多,充放电电压曲线和电流曲线也随之变化,充放电曲线的形状与电池的老化情况高度相关.如何从充放电曲线中提取出与SOH高度敏感的特征参数是SOH估计的关键.但不同充电策略所对应的敏感特征参数可能不同,很难找到普适于多个充电策略的特征参数.当前有关锂电池SOH估计方法大多针对某一特定充电策略,没有考虑充电策略的不同及其进一步发展.为此,提出一种更泛化的特征参数提取流程.首先,充分分析不同充电策略的单体电池在不同循环次数下电压、电流、IC曲线变化特性,并参考文献[2,6,15]中的结论,从IC曲线提取IC曲线峰值(PIC)、IC曲线峰值对应电压(UIC)、IC曲线峰左斜率(kL)、IC曲线峰右斜率(kR) 4个特征,如图4(a)所示;从电流曲线提取CV充电下降到给定电流所用时间(tD)和CV充电过程最后阶段的平均电流(IA),如图4(b)所示;从电压曲线提取CC充电上升到给定电压所用时间(tU)和单次循环后静置时间内的电压回升数值(UV),如图4(c)所示.然后,为了适应不同充电策略,采用交叉验证方法自动选择针对特定充电策略的个性化最优特征参数.交叉验证方法在上述所提取的通用特征集中遍历所有可能的特征参数组合, 然后对各个特征组合的估计结果进行排序以选出最优特征参数组合.

图3 某单体电池充放电曲线在不同循环周期下的变化情况Fig.3 Change of voltage and current in charging and discharging of a single battery of different cycles

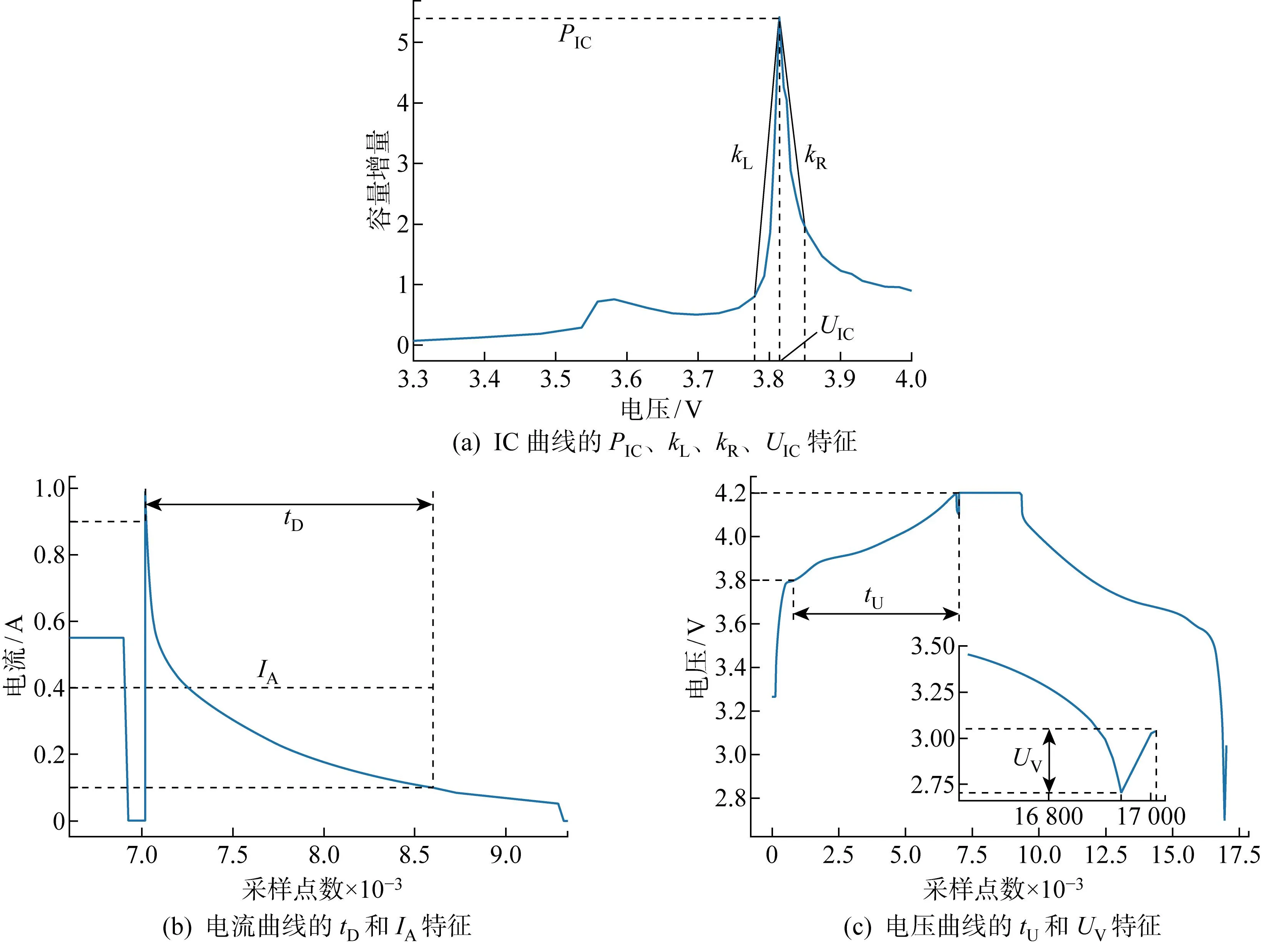
图4 电流、电压和IC曲线的提取特征Fig.4 Extracted features from current, voltage, and IC curve

2.3 分位数回归

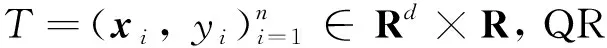
i=1, 2, …,t;τ=τ1,τ2, …,τM

(1)

式中:xi=[xi,1xi,2…xi,d]为包含d个分量的独立变量,xi,j是xi的第j个分量,j=1, 2, …,d;yi为对应xi的因变量;qτ(xi)为因变量yi在自变量xi下的第τ分位数,对于任意分位数0<τ<1,β(τ)=[β1(τ)β2(τ) …βd(τ)]′为τ分位数下的回归系数.β(τ)的估计值通过最小化检验函数ρτ(σ)获得.

(2)

检验函数ρτ(σ)为一分段线性函数,定义为

ρτ(σ)=σ(τ-I(σ))

(3)

式中:I(σ)为一个指示函数,定义为

(4)

2.4 支持向量分位数回归

(5)

(6)

s.t.yi-wTφ(xi)-b≤ξi

Shim等[25]采用半参数方法通过构造拉格朗日函数的方法对式(6)优化问题进行求解,即

(7)

(8)

式中:xs、xt为任意变量;σK为核函数的宽度.采用广义近似交叉验证准则[26]获得最优超参数组合,即

(9)

3 实验设计

3.1 实验设置

采用3个具有不同充电策略的公开数据集来验证所提方法的有效性.分别为马里兰大学高级生命周期工程中心公开数据集(简称CALCE)[27]、牛津电池老化数据集(简称Oxford)[28]和麻省理工-斯坦福-丰田研究中心电池数据集(简称TRI)[29].3个数据集的基本信息如表1所示,更为详细的信息可参阅文献[27-29].图5分别以每个数据集中的1个电池为例,展示3个数据集各自电池容量随循环次数的变化情况.可见尽管电池容量都随循环次数增加而下降,但不同数据集的变化情况不同.

表1 3个数据集的基本信息Tab.1 Basic information of three datasets

图5 CALCE、Oxford、TRI数据集电池容量变化Fig.5 Battery capacity change of CALCE, Oxford and TRI datasets

在每个数据集中选用1个放电程度较深的单体电池充放电数据作为训练集,在其余单体电池中任选3个作为测试集来验证所提方法的性能.所选训练集和测试集的情况如表2所示.

表2 训练集和测试集情况Tab.2 Basic information of training set and test set

3.2 参与比较的方法

所提方法的优势在于两个方面:①可以适用于不同的充电策略;②采用的SVQR方法可以在小样本数据集上更好地进行SOH区间估计.第一个优势显而易见,如文献[13-14]的方法都针对某一特定充电策略,在遇到不同充电策略时所提取的特征参数不再适用.为此,在实验部分重点论证所采用的SVQR相比于其他区间预测方法的优越性.首先对比SVQR与QR、QRNN,QR把分位数的概念融入普通的线性回归中,本质上是一种线性方法;QRNN将分位数概念与神经网络结合以解决非线性回归问题.此外,最近GPR被报道在处理锂电池SOH区间估计方面具有优秀性能[15],因此还将SVQR方法与GPR方法进行对比.

3.3 评价指标

为全面验证所提方法的性能,采用如下3个指标来评价SOH区间估计结果的优劣:平均区间分数(Average Interval Score, AIS)[30]、平均预测区间中心偏差(Mean Prediction Interval Center Deviation, MPICD)[31]以及平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)[32].上述指标包含对估计结果区间宽度、区间覆盖率以及估计偏差等信息的衡量,各自定义如下:

(1) AIS指标.AIS指标定义为所有区间估计点的区间分数均值,可综合衡量区间覆盖率和区间宽度,其值越大越优,按下式计算.

(10)

式中:α为置信区间宽度;Ntest为测试集电池循环次数;S(α)(xi)为第i个估计区间的区间分数,定义为

S(α)(xi)=

(11)

(2) MPICD指标.MPICD表示预测区间中心位置与实际值的偏差,该值越小越优,按下式计算.

(12)

(3) MAPE指标.MAPE按下式计算,该指标可衡量预测区间的宽度信息,狭窄的区间比宽大的区间更好.

(13)

式中:Li、Ui分别为预测下限和上限.

4 实验结果与分析

经过特征提取和交叉验证特征自动优选过程,最终对CALCE数据集选择IC曲线峰值、IC曲线峰值对应电压、IC曲线左斜率、CC充电上升到给定电压所用时间、CV充电下降到给定电流所用时间5个特征;对Oxford数据集选择IC曲线峰值、IC曲线左斜率、IC曲线右斜率3个特征;对TRI数据集选择IC曲线峰值、IC曲线右斜率、CV充电下降到给定电流所用时间3个特征.为了实验对比的公平性,其余3种方法在评估时针对不同的数据集采用与SVQR方法同样的特征参数.表3～5分别展示所提方法与QR、QRNN和GPR方法分别在CALCE、Oxford和TRI数据集中各自任选的3个单体电池上的SOH评估结果,其中用粗体标出的为最优结果.图6～8分别展示4种方法在3个数据集中CS35、Cell7、b0c32这3个电池上的SOH估计效果.

首先,从图6～8和表3～5可以看出,在所有数据集上,对于所有的评价指标QRNN与QR结果比较接近,但都远劣于SVQR;QRNN略优于QR,这印证了QR本质上是线性回归方法,其在处理锂电池SOH非线性估计上性能不足.而QRNN性能远劣于SVQR,这充分印证了在本文数据集的量级上,SVQR处理小样本非线性问题时具有更好的泛化能力.其次,在所有实验中SVQR方法的结果与GPR接近,但在多数电池上多数指标都优于GPR方法.尤其在MAPE指标方面,SVQR方法在所有数据集上全优于GPR.AIS指标方面,SVQR方法在Oxford和TRI数据集上均取得最好结果,仅在CALCE数据集上,劣于GPR方法;MPICD指标方面,SVQR方法在CALCE和Oxford数据集上除Cell7电池外,均明显优于GPR,仅在TRI数据集上略劣于GPR.文献[15]报道,GRP方法是目前处理锂电池SOH估计的最优方法.但实际上,GPR需要假设数据服从高斯分布,而实测的锂电池充放电数据涉及复杂过程和噪声干扰,很难确保满足高斯假设.本文所提SVQR则无需此假设,这可以解释上述实验中SVQR总体优于GPR的原因.另外值得指出的是,实验采用同一充电协议下的某一放电深度较深电池的全生命期循环充放电数据来训练SVQR模型,用同数据集中其他电池来测试,这与其他多数研究采用同一电池的部分充放电数据来预测其剩余循环的退化情况相比更有实际意义.上述结论充分证明本文方法在SOH估计方面的优势.

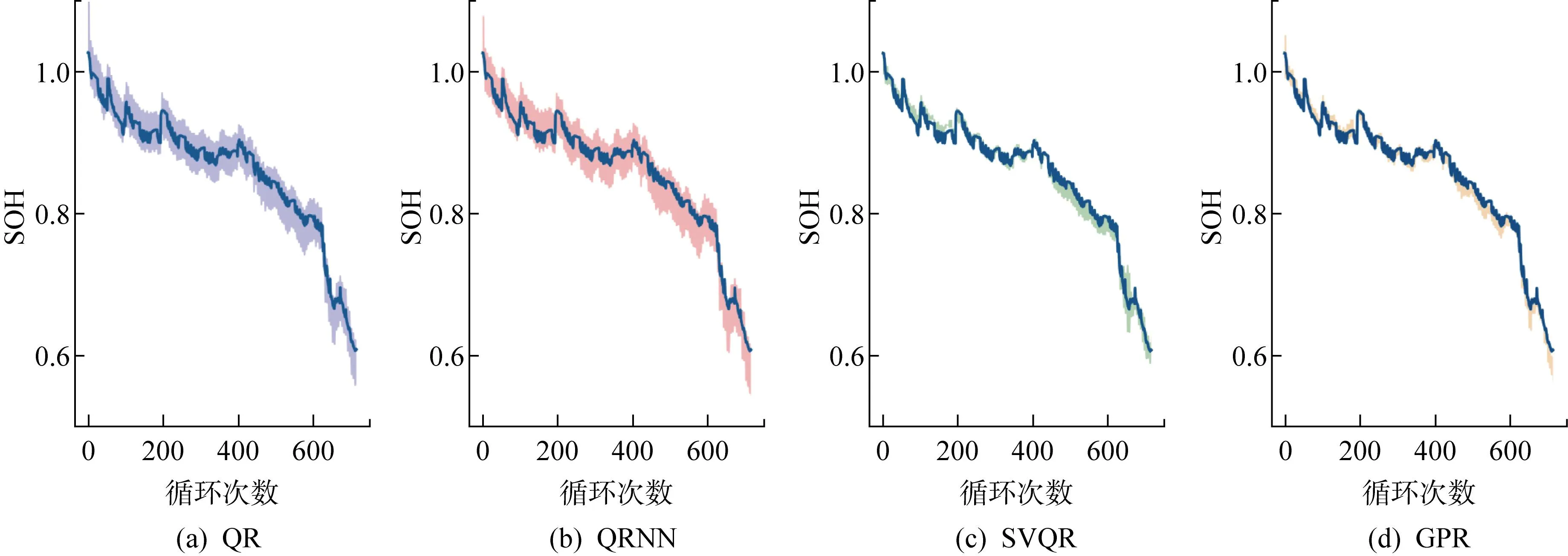
图6 4种方法在CALCE数据集CS35电池的SOH区间估计对比结果Fig.6 Comparison of four methods for estimating SOH interval of CS35 battery in CALCE dataset

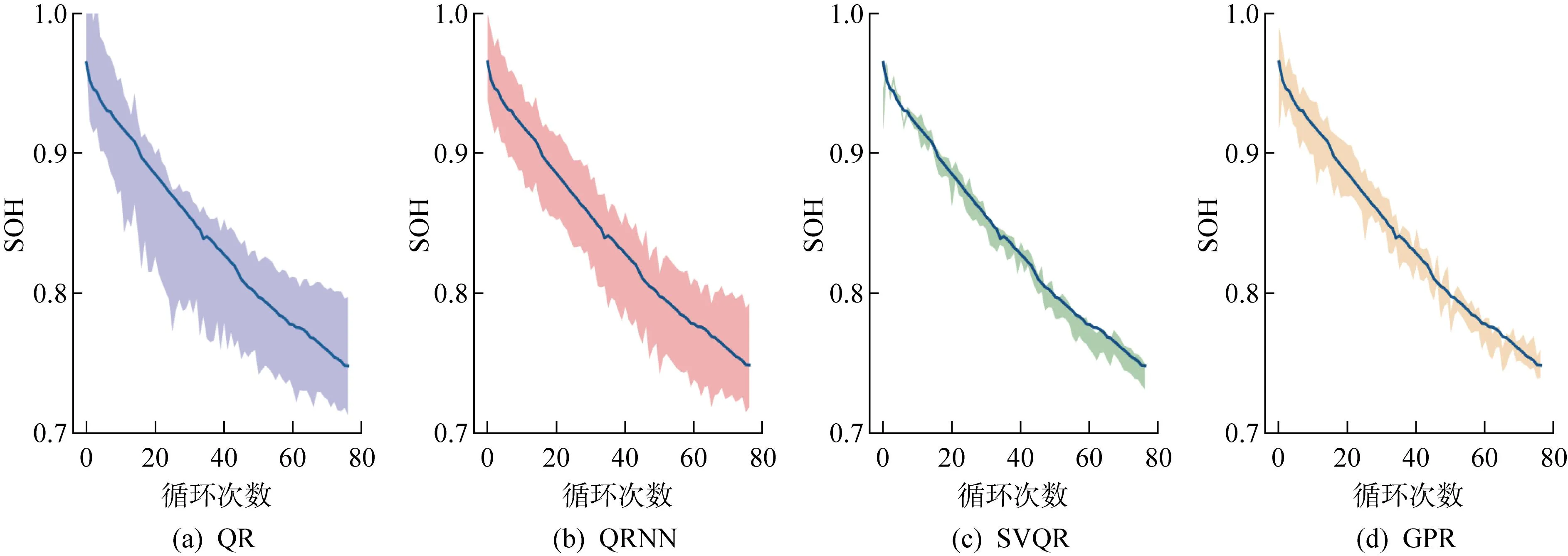
图7 4种方法在Oxford数据集Cell7电池的SOH区间估计对比结果Fig.7 Comparison of four methods for SOH interval estimation of Cell7 battery in Oxford dataset

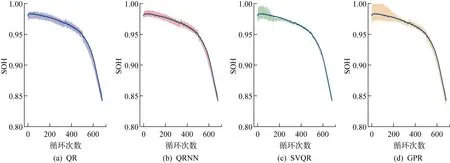
图8 4种方法在TRI数据集b0c32电池的SOH区间估计对比结果Fig.8 Comparison of four methods in estimating SOH interval of b0c32 battery in TRI dataset

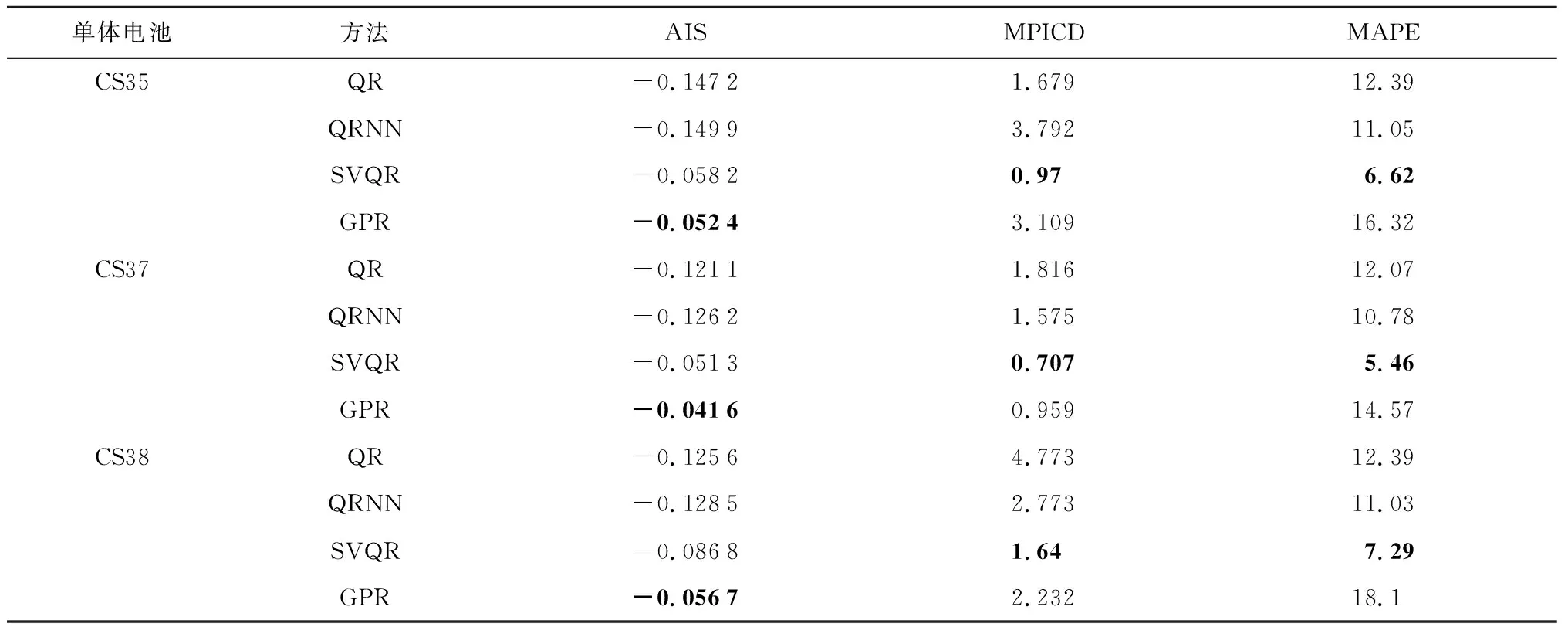
表3 CALCE数据集3个单体电池的SOH估计对比结果Tab.3 Comparison of SOH estimation of three single cells in CALCE dataset 10-3

5 结论

提出一种考虑不同充电策略的锂电池剩余容量SVQR区间估计方法.该方法在离线阶段,从锂电池充放电电压、电流及容量增量曲线中获取多个特征,并采用交叉验证方法自动选择最优特征组合.选取放电程度较深的单体电池循环充放电数据训练SVQR模型.在SOH在线估计阶段,采用和训练模型相同的特征作为模型输入,对服役中的锂电池进行SOH区间估计.最后在3个采用不同充电策略的数据集验证所提方法,并与QR、QRNN和GPR方法进行对比,可得出以下结论:

(1) 在不同充电策略下,利用相同外部特征对于锂电池SOH的估计结果也不同.采用两步特征提取策略,即首先针对不同充电策略提取足够多特征,再选取针对不同电池及充电策略的个性化特征参数,可以显著提高电池SOH估计的精度,且具有良好的普适性.

(2) 神经网络类方法的训练需要较大数据集样本,但在样本量有限的锂电池充放电数据集中神经网络类算法估计效果有限.而SVQR利用SVR算法适用于小样本数据集的特点,即使是在小样本条件下也可以较好地在置信区间内估计锂电池SOH.

(3) 相较于文献报告的当前最优的GPR方法,所提SVQR方法无需原始数据服从高斯分布,可在一定置信区间内实现较好的SOH估计结果,具有更好的适应性和鲁棒性.